Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
СИСТЕМЫ СЧИСЛЕНИЯ. ПРЕДСТАВЛЕНИЕ ЧИСЕЛ В КОМПЬЮТЕРЕ
Содержание
- 1. СИСТЕМЫ СЧИСЛЕНИЯ. ПРЕДСТАВЛЕНИЕ ЧИСЕЛ В КОМПЬЮТЕРЕ
- 2. Система счисления– это способ отображения чисел с
- 3. НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯЕдиничная (палочная)В этой системе счисления
- 4. Римская нумерацияЗаписывались цифры числа начиная с больших
- 5. Славянская кириллическая нумерацияЭта нумерация была создана для
- 6. Китайская нумерацияВозникла эта нумерация около 4 000
- 7. Греческая нумерацияВ древнейшее время в Греции была
- 8. Непозиционные системы счисленияПредставление через биномиальные коэффициентыСистема остаточных
- 9. ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯСистемы счисления, основанные на позиционном
- 10. Слайд 10
- 11. Известный математик и физик XVIII–XIX века П.
- 12. Позиционная, двоичнаяВ двоичной системе счисления используются всего
- 13. Позиционная, троичная. Симметричная и несимметричная Трит –
- 14. Преимущества троичной симметричной системы (-1, 0, 1)естественное
- 15. Позиционные системы счисленияДесятичнаяДвоичнаяВосьмеричнаяШестнадцатеричнаяТроичная (электроника +,0,-)Двенадцатеричная (счет дюжинами)Шестидесятеричная
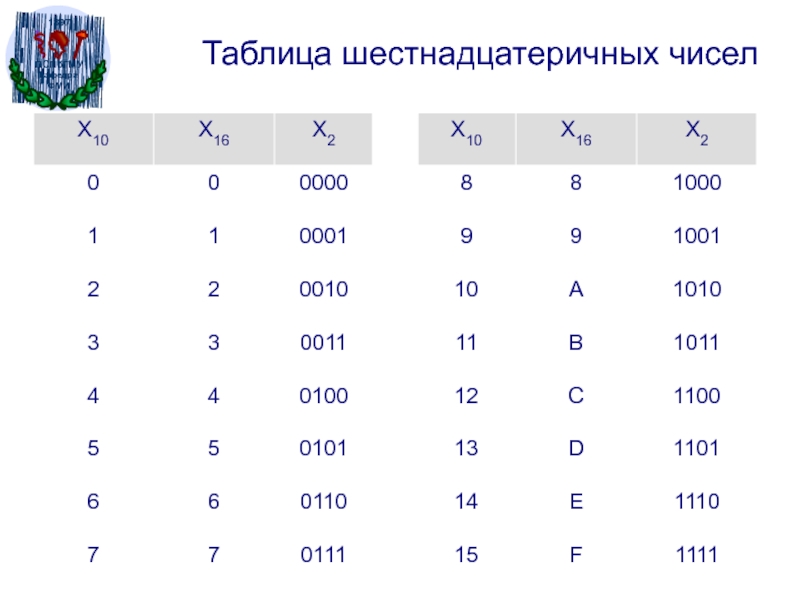
- 16. Таблица шестнадцатеричных чисел
- 17. Смешанные системы счисленияДата – год, месяц, деньВремя
- 18. Представление числа в позиционной системе счисленияan-1an-2 …a1a0
- 19. Перевод целых чисел из десятичной системы
- 20. Перевод правильной десятичной дроби из десятичной
- 21. Перевод чисел в десятичную систему счисления
- 22. Перевод из восьмеричной и шестнадцатеричной системы счисления
- 23. Перевод из двоичной системы счисления в
- 24. Перевод из восьмеричной системы счисления в
- 25. Арифметические операции в позиционных системах счисления
- 26. Если при умножении однозначных
- 27. Сложение в позиционных системах счисленияЦифры суммируются по
- 28. Вычитание в позиционных системах счисленияПри вычитании чисел,
- 29. Умножение в позиционных системах счисления
- 30. Умножение в шестнадцатеричной системе счисленияОТВЕТ: 169В97416
- 31. Деление в позиционных системах счисления
- 32. Представление чисел в компьютереформат с фиксированной
- 33. Целые числа со знаком занимают в
- 34. В компьютерной технике применяются три формы записи
- 35. Дополнительный код используется для представления отрицательных чисел,
- 36. Отрицательные десятичные числа при вводе в компьютер
- 37. Определим диапазон чисел, которые могут храниться в
- 38. Представление вещественных чисел в компьютереЛюбое число
- 39. Способ представления числа с плавающей запятой, опирается
- 40. Порядок и мантисса определяют диапазон изменения чисел
- 41. При записи основания числа в десятичной системе
- 42. Выполнение арифметических операций над числами с
- 43. В 1976 г. была принята инициатива создать
- 44. IEEE 754 - стандарт двоичной арифметики
- 45. В IEEE754 число «0» представляется значением с
- 46. Все компьютеры поддерживают несколько международных стандартных форматов,
- 47. В компьютере, число с плавающей запятой представляется
- 48. Стандартные форматы представления вещественных чисел:Вещественный формат с m-разрядной
- 49. Алгоритм представления числа с плавающей запятой
- 50. ПримерПредставить число -25,625 в машинном виде с
- 51. Информация почти всегда является ответом. Наиболее
- 52. Кодирование текстовой информацииСоответствие между набором символов и
- 53. ПримерС помощью кодировок ASCII и Unicode закодирована
- 54. С помощью кодировок ASCII и Unicode закодирована
- 55. Формула ХартлиДля измерения количества информации, которое может
- 56. Кодирование графической информации
- 57. В текстовом режиме экран разбивается на 25
- 58. Кодирование звуковой информацииСуществует (1999 г.) два способа
- 59. Аналоговый сигналКВАНТОВАНИЕДИСКРЕТИЗАЦИЯИнтервал дискретизации1 1 11 1 01
- 60. КОНТРОЛЬНЫЕ ВОПРОСЫ:Перечислите типы систем счисления.Что является основанием
- 61. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1СИСТЕМЫ СЧИСЛЕНИЯ.
ПРЕДСТАВЛЕНИЕ ЧИСЕЛ В КОМПЬЮТЕРЕ
Зав. кафедрой, к.ф.-м.наук
Тишков Артем
Валерьевич
Слайд 2Система счисления
– это способ отображения чисел с помощью символов или
совокупность правил именования и изображения чисел с помощью набора символов,
называемых цифрами.Используются три типа систем счисления:
позиционная – представление числа зависит от порядка записи цифр.
непозиционная – представление числа не зависит от порядка записи цифр
смешанная – нет понятия «основание»: либо оснований несколько, либо оно вычисляемое
«Письменность, это величайшее изобретение руки и ума человека, постепенно возникла из счета»
Дж. Бернал, английский ученый и философ
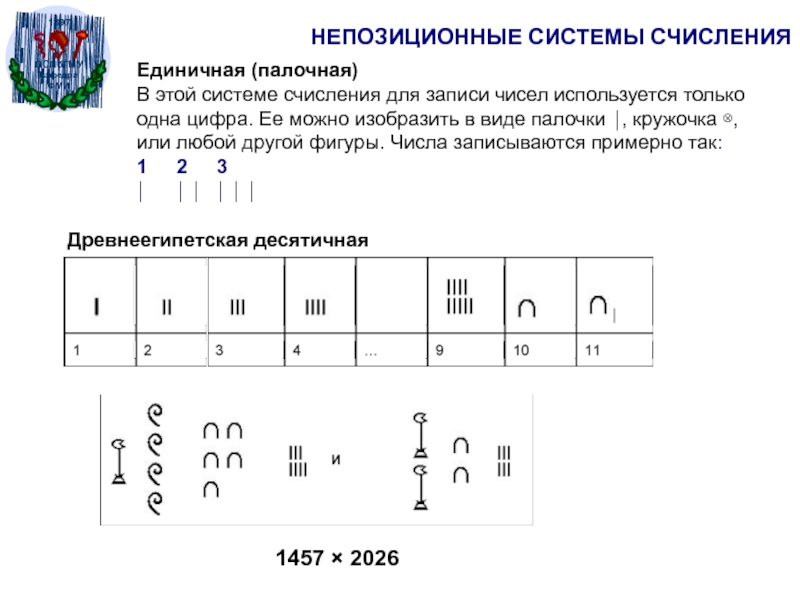
Слайд 3НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Единичная (палочная)
В этой системе счисления для записи чисел
используется только одна цифра. Ее можно изобразить в виде палочки
, кружочка , или любой другой фигуры. Числа записываются примерно так:1 2 3
Древнеегипетская десятичная
1457 2026
Слайд 4Римская нумерация
Записывались цифры числа начиная с больших значений и заканчивая меньшими,
слева направо. При записи цифры с меньшим значением перед цифрой
с большим значением происходит ее вычитание.CCXXXVII = 100+100+10+10+10+5+1+1 = 237, но XXXIX = 10+10+10-1+10 = 39
Правило: нельзя записывать подряд 4 одинаковых цифры, такая комбинация заменяется комбинацией с правилом вычитания, например: XXXX = XC (50-10)
IIII = IV (5-1), CCCC = CD (500-100)
Слайд 5Славянская кириллическая нумерация
Эта нумерация была создана для переписки священных книг
для славян греческими монахами братьями Кириллом (Константином) и Мефодием в IX
веке. До XVII века эта форма записи чиcел была официальной на территории современной России, Белоруссии, Болгарии, Венгрии, Сербии и Хорватии. До сих пор православные церковные книги используют эту нумерацию.Интереснее всего записывались числа второго десятка:
Читаем дословно «четырнадцать» – «четыре на десять» 4+10, и так для всех чисел от 11 до 19.
800+60+3.
Для того, чтобы не перепутать буквы и цифры, использовалась титла - горизонтальная черточка над числами.
Для обозначения больших, чем 900 чисел использовались специальные значки, добавляемые к букве, буква бралась в кружочек.
Слайд 6Китайская нумерация
Возникла эта нумерация около 4 000 тысяч лет тому
назад в Китае.
1 2 3 4 5 6 7 8 9 0Использовали несколько служебных иероглифов, чтобы не перепутать разряды.
10 100 1000
Такая запись числа мультипликативна:
11 000 и 5100 + 410+8
Слайд 7Греческая нумерация
В древнейшее время в Греции была распространена так называемая
Аттическая нумерация. В этой нумерации числа 1, 2, 3, 4
изображались соответствующим количеством вертикальных полосок: , , , . Число 5 записывалось знаком (древнее начертание буквы «Пи», с которой начиналось слово «пять» - «пенте». Числа 6, 7, 8, 9 обозначались сочетаниями этих знаков: .Число 10 обозначалось – заглавной »Дельта» от слова «дека» – «десять». Числа 100, 1 000 и 10 000 обозначались H, X, M. Числа 50, 500, 5 000 обозначались комбинациями чисел 5 и 10, 5 и 100, 5 и 1 000.
Примерно в третьем веке до нашей эры аттическая нумерация в Греции была вытеснена другой, так называемой «Ионийской» системой.
В ней числа 1 – 9 обозначаются первыми буквами греческого алфавита:
числа 10, 20, … 90 изображались следующими девятью буквами;
числа 100, 200, … 900 последними девятью буквами.
Примерно по такому же принципу организованную систему счисления имели в древности евреи, арабы и многие другие народы Ближнего Востока.
Слайд 8Непозиционные системы счисления
Представление через биномиальные коэффициенты
Система остаточных классов (СОК)
Определяется набором
взаимно простых модулей (m1, m2, …, mn,)
с произведением M =
m1 * m2 * … * mn так, что каждому целому числу x из отрезка [0, M –1] ставится в соответствие набор (x1, x2, …, xn) вычетов j x ≡ x1 (mod m1);
x ≡ x2 (mod m2);
x ≡ xn (mod mn);
0 ≤ c1 < c2 < … < cn
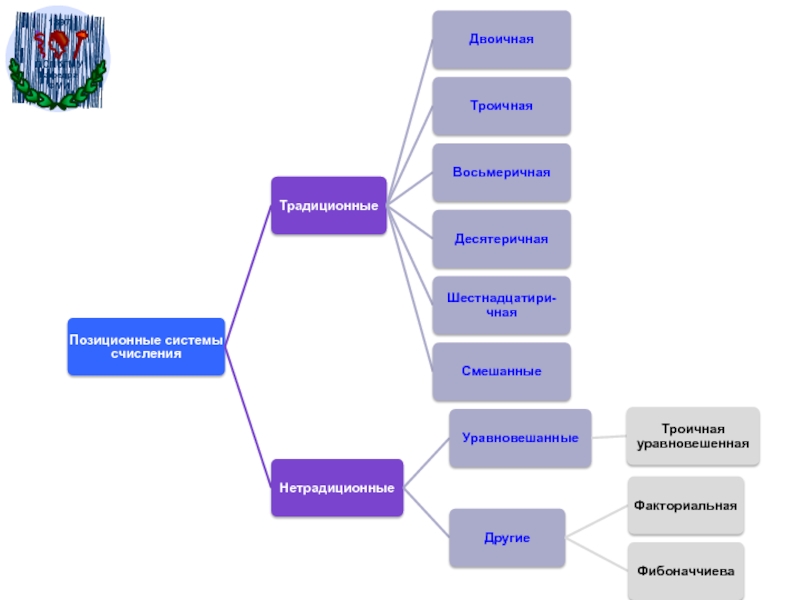
Слайд 9ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Системы счисления, основанные на позиционном принципе, возникли независимо
друг от друга в трех местах: в Древнем Вавилоне, у
племени Майя и в Индии.Каждая цифра обозначает число по количеству углов в ней.
Например, 0 – углов нет, 1 – один угол, 2 – два угла и т.д.
Появление нуля
Цифрой 0 обозначается отсутствующая величина.
Древние греческие астрономы (II век до н.э.) для обозначения нулевого значения разряда использовали символ 0 (по первой букве греческого слово ничто). Этот знак и был прообразом современного нуля. Индийцы переняли общетеоретические положения этой науки и многие греческие термины. Соединив свою десятичную мультипликативную систему с принципами нумерации чисел греческих астрономов, индийские ученые сделали завершающий шаг в создании всем известной десятичной системы счисления.
Слайд 11Известный математик и физик XVIII–XIX века П. Лаплас говорил:
«Мысль
выражать все числа десятью знаками, придавая им, кроме значения по
форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно понять, насколько она удивительна. Как нелегко было прийти к этому методу, мы видим на примере величайших гениев греческой учености Архимеда и Апполония, от которых эта мысль осталась скрытой.»Позиционная, двоичная
Логика: истина / ложь
В повседневной жизни: Да / Нет
В повседневной жизни: Есть / Нет
В технике: электрический сигнал есть / нет
0 / 1, бит
Слайд 12Позиционная, двоичная
В двоичной системе счисления используются всего 2 состояния или
2 цифры. Такое представление информации принято считать двоичным кодированием.
Великий немецкий
математик Г.Ф. Лейбниц видел в ней «….прообраз творения». Он считал, что «единица представляет божественное начало, а нуль – небытие. Высшее существо создает все сущее из небытия точно таким же образом, как единица с помощью нуля выражает все числа».Вся информация, обрабатываемая компьютерами хранится в двоичном виде в ячейках памяти, а обрабатывается – в регистрах арифметико–логического устройства (АЛУ). И регистр и ячейка памяти представляет собой физическую систему, состоящую из некоторого числа однородных элементов, которые называются разрядом.
Нумерация справа → налево:
(n–1)-й разряд 0-й разряд
ячейка из n-разрядов
Слайд 13Позиционная, троичная.
Симметричная и несимметричная
Трит – троичный триггер
1 Трайт =
6 тритов, 729 значений (байт – 256)
Советская машина Сетунь –
первая и единственная серийная троичная машина. 1962-1965 годы10Ī = 9 − 1 = 8
Ī01 = −9 + 1 = −8
Слайд 14Преимущества троичной симметричной системы (-1, 0, 1)
естественное представление чисел со
знаком (не нужен прямой, обратный или дополнительный код!)
знак числа -
это знак старшей ненулевой цифры и не нужен знаковый битПростое сравнение чисел по величине, при этом не нужно смотреть на знак
поэтому команда ветвления по знаку в троичной машине работает вдвое быстрее, чем в двоичной
усечение длины числа равносильно правильному округлению (округление в двоичных машинах не обеспечивают этого)
троичный сумматор осуществляет вычитание при инвертировании одного из слагаемых, откуда следует, что троичный счетчик автоматически является реверсивным (обеспечивает и сложение и вычитание
в трехвходовом троичном сумматоре перенос в следующий разряд возникает в 8 ситуациях из 27, а в двоичном сумматоре - в 4 из 8. В четырехвходовом сумматоре перенос также происходит только в соседний разряд.
таблицы умножения и деления почти так же просты, как и в двоичной системе
умножение на -1 инвертирует множимое
трехуровневый сигнал более устойчив к воздействию помех в линиях передачи. Это означает что специальные методы избыточного кодирования троичной информации проще, нежели двоичной
Слайд 15Позиционные системы счисления
Десятичная
Двоичная
Восьмеричная
Шестнадцатеричная
Троичная (электроника +,0,-)
Двенадцатеричная (счет дюжинами)
Шестидесятеричная (время, углы –
широта долгота)
Количество цифр называют основанием
позиционной системы счисления, а позиции
цифр
в числе – разрядами.Алфавит
Двоичная система счисления – 0, 1
Восьмеричная система счисления – 0, 1, 2, 3, 4, 5, 6, 7
Шестнадцатеричная система счисления –
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
10, 11, 12, 13, 14, 15
Слайд 17Смешанные системы счисления
Дата – год, месяц, день
Время – часы, минуты,
секунды, миллисекунды
при этом величина h часов, m минут, s секунд
соответствуетT = h * 60 * 60 + m * 60 + s
Углы – градусы, минуты, секунды
Смешанной называется система счисления, в которой числа, заданные в некоторой системе счисления с основанием P (например – время) изображаются с помощью цифр другой системы счисления с основанием Q (например – секунды), где Q
Слайд 18Представление числа в позиционной системе счисления
an-1an-2 …a1a0 , a-1…a-m
Запись чисел
в каждой из систем счисления с основанием q означает сокращенную
запись выраженияan-1qn-1 + an-2qn-2 + … + a1q1 + a0q0 + a-1q-1 + … + a-mq-m,
где ai – цифры численной записи, соответствующие разрядам, i – индекс, n и m – количество разрядов числа целой и дробной части соответственно, q – основание системы счисления.
Например, развернутая форма числа 327,46
n = 3, m = 2, q = 10
X = = a2*102+ a1*101 +a0*100+ a-1*10-1+ a-2*10-2 =
3*102 + 2*101 + 7*100 + 4*10-1 + 6*10-2
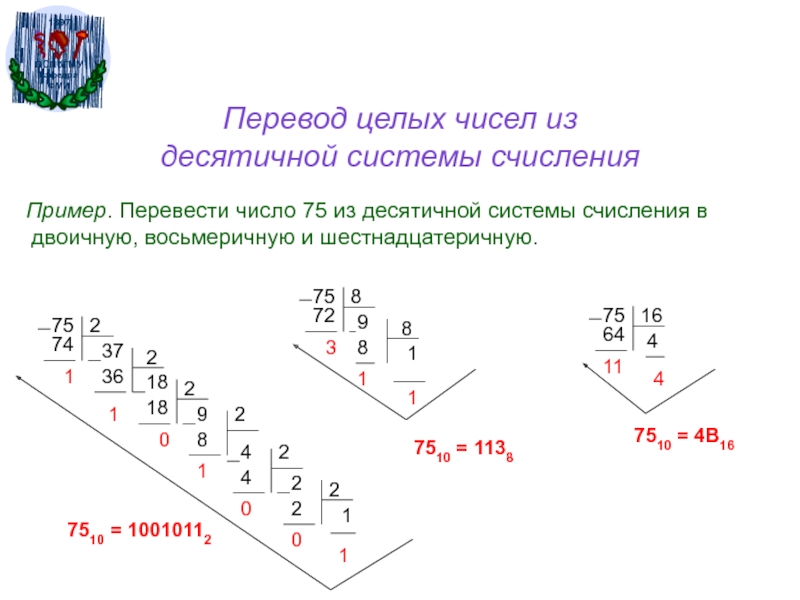
Слайд 19Перевод целых чисел из
десятичной системы счисления
Пример. Перевести
число 75 из десятичной системы счисления в двоичную, восьмеричную и
шестнадцатеричную.75
2
74
1
37
2
36
1
18
2
18
0
9
2
8
1
4
2
4
0
2
2
2
0
1
1
7510 = 10010112
75
8
72
3
9
8
8
1
1
1
7510 = 1138
75
16
64
11
4
4
7510 = 4B16
Слайд 20Перевод правильной десятичной дроби
из десятичной системы счисления
Пример. Перевести число
0,35 из десятичной системы в счисления в двоичную, восьмеричную и
шестнадцатеричную.0,35
2
0,70
2
1,40
2
0,80
2
1,60
2
1,20
0,3510 = 0,010112
0,35
8
2,80
8
6,40
8
3,20
0,3510 = 0,2638
0,35
16
5,60
16
9,60
0,3510 = 0,5916
Слайд 21Перевод чисел в десятичную систему счисления
Пример. Перевести число
1011,1 из двоичной системы счисления в десятичную.
Пример. Перевести
число 276,8 из восьмеричной системы счисления в десятичную. Пример. Перевести число 1F3 из шестнадцатеричной системы счисления в десятичную.
1 F 316
0
1
2
= 1∙162 + 15∙161 + 3∙160 = 49910
разряды
число
Слайд 22Перевод из восьмеричной и шестнадцатеричной системы счисления в двоичную
Заменить каждую цифру восьмеричного/шестнадцатеричного числа соответствующим трехразрядным/четырехразрядным двоичным кодом.
1A3,F16
= Пример. Перевести число 527,18 в двоичную систему счисления.
2
Пример. Перевести число 1A3,F16 в двоичную систему счисления.
Слайд 23Перевод из двоичной системы счисления
в восьмеричную и шестнадцатеричную
Для перехода от двоичной к восьмеричной/шестнадцатеричной системе счисления поступают
следующим образом: двигаясь от запятой влево и вправо, разбивают двоичное число на группы по 3(4) разряда, дополняя, при необходимости, нулями крайние левую и правую группы. Затем каждую группу из 3(4) разрядов заменяют соответствующей восьмеричной/шестнадцатеричной цифрой.Пример:
0
0
000
Слайд 24Перевод из восьмеричной системы счисления
в шестнадцатеричную и обратно
При переходе из восьмеричной системы счисления в шестнадцатеричную и
обратно вначале производится перевод чисел из исходной системы счисления в двоичную, а затем – в конечную систему .Пример. Перевести число 527,18 в шестнадцатеричную систему счисления.
Пример. Перевести число 1A3,F16 в восьмеричную систему счисления.
Слайд 25Арифметические операции в позиционных системах счисления
Правила выполнения
основных арифметических операций в любой позиционной системе счисления подчиняются тем
же законам, что и в десятичной системе.При сложении цифры суммируются по разрядам, и если при этом возникает переполнение разряда, то производится перенос в старший разряд. Переполнение разряда наступает тогда, когда величина числа в нем становится равной или большей основания системы счисления.
При вычитании из меньшей цифры большей в старшем разряде занимается единица, которая при переходе в младший разряд будет равна основанию системы счисления
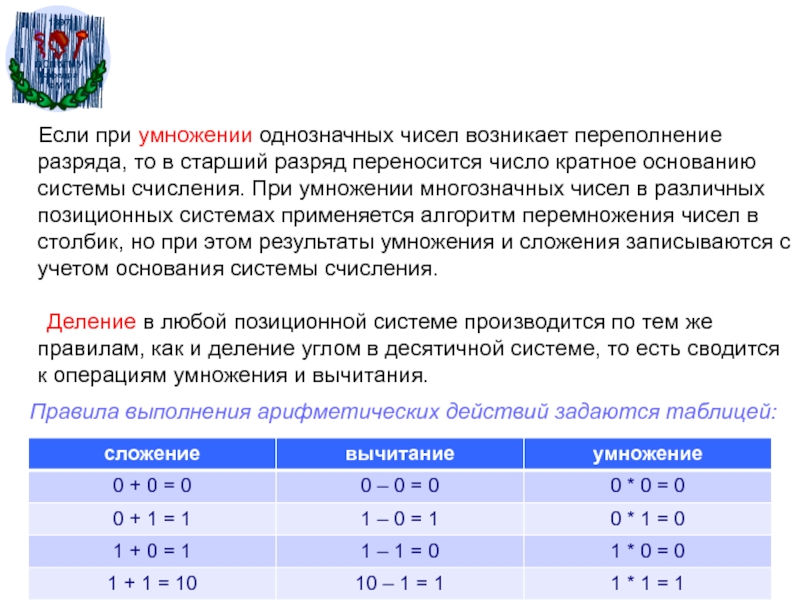
Слайд 26 Если при умножении однозначных чисел возникает переполнение
разряда, то в старший разряд переносится число кратное основанию системы
счисления. При умножении многозначных чисел в различных позиционных системах применяется алгоритм перемножения чисел в столбик, но при этом результаты умножения и сложения записываются с учетом основания системы счисления.Деление в любой позиционной системе производится по тем же правилам, как и деление углом в десятичной системе, то есть сводится к операциям умножения и вычитания.
Правила выполнения арифметических действий задаются таблицей:
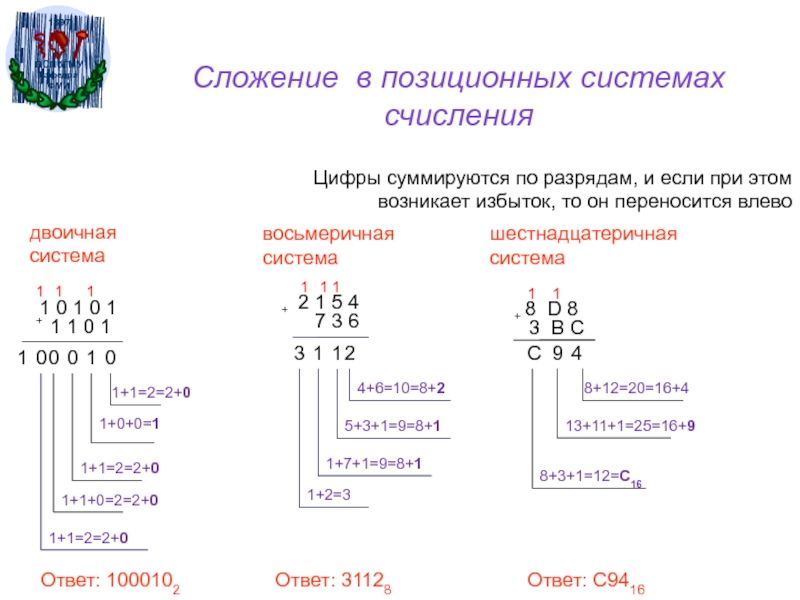
Слайд 27Сложение в позиционных системах
счисления
Цифры суммируются по разрядам, и если при
этом возникает избыток, то он переносится влево
Слайд 28Вычитание в позиционных системах счисления
При вычитании чисел, если цифра уменьшаемого
меньше цифры вычитаемого, то из старшего разряда занимается единица основания
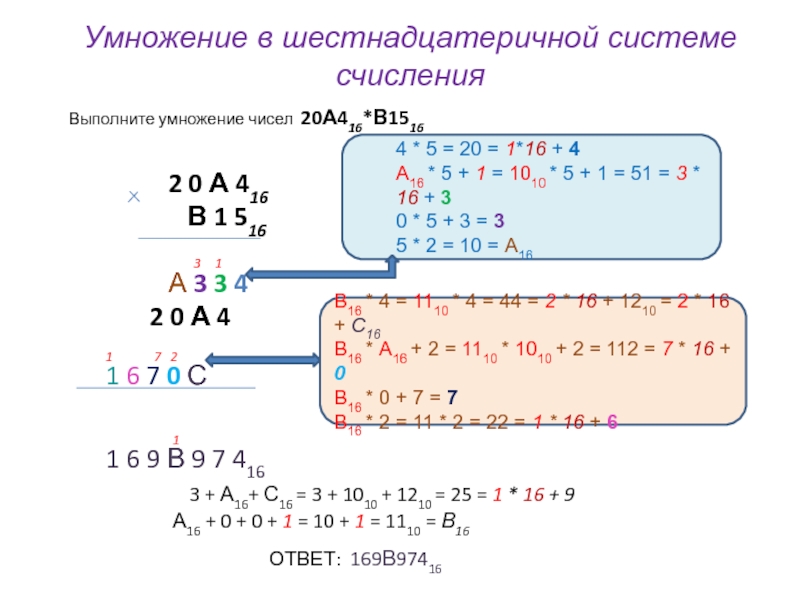
Слайд 29Умножение в позиционных системах счисления
При умножении
многозначных чисел в различных позиционных системах применяется алгоритм перемножения чисел
в столбик, но при этом результаты умножения и сложения записываются с учетом основания системы счисленияСлайд 31Деление в позиционных системах счисления
Деление в
любой позиционной системе производится по тем же правилам, как и
деление углом в десятичной системе. При этом необходимо учитывать основание системы счисления.Слайд 32Представление чисел в компьютере
формат с фиксированной запятой – целые
числа
формат с плавающей запятой – вещественные числа
Вещественные числа хранятся и
обрабатываются в компьютере в формате с плавающей запятой. Этот формат базируется на экспоненциальной форме записи, в которой может быть записано любое число.Целые числа в компьютере могут представляться со знаком или без знака.
Целые числа без знака занимают в памяти один или два байта.
Пример. Число 7210 = 10010002 в однобайтовом формате
Слайд 33 Целые числа со знаком занимают в памяти компьютера один,
два или четыре байта, при этом самый левый (старший) разряд
содержит информацию о знаке числа.Знак «плюс» кодируется нулем, а «минус» - единицей
Пример. Число –7210 = –10010002 в однобайтовом формате
Пример. Число 6210 = 1111102 в однобайтовом формате
Слайд 34В компьютерной технике применяются три формы записи (кодирования) целых чисел
со знаком:
прямой код, обратный код и дополнительный код.
Прямой код
– чаше всего отводится 2 байта памяти (16 бит), в старший разряд записывается «0» если число положительное и «1» – если число отрицательное. Обратный код – для положительных чисел совпадает с прямым кодом, для отрицательных чисел образуется из прямого кода заменой нулей единицами, а единиц – нулями, кроме цифр знакового разряда.
Пример. Число -5710 = -1110012
прямой
обратный
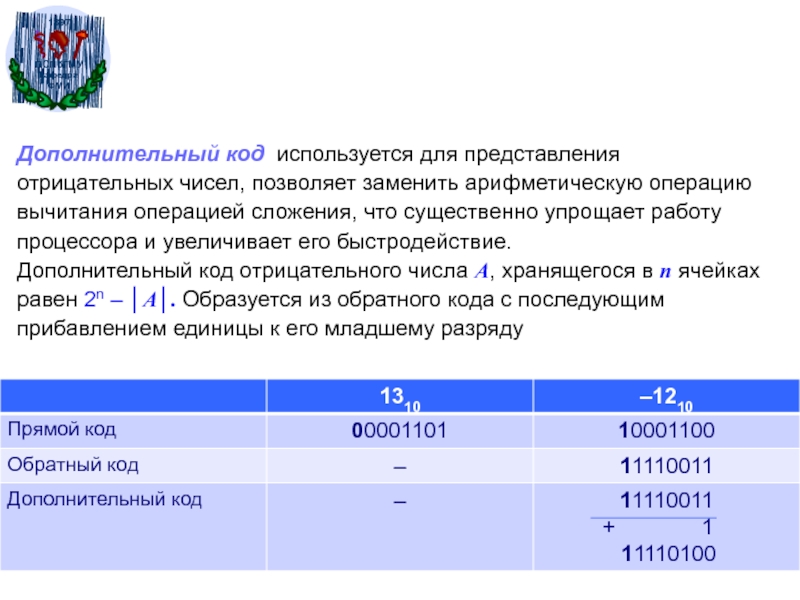
Слайд 35Дополнительный код используется для представления отрицательных чисел, позволяет заменить арифметическую
операцию вычитания операцией сложения, что существенно упрощает работу процессора и
увеличивает его быстродействие.Дополнительный код отрицательного числа А, хранящегося в n ячейках равен 2n – │A│. Образуется из обратного кода с последующим прибавлением единицы к его младшему разряду
Слайд 36Отрицательные десятичные числа при вводе в компьютер автоматически преобразуются в
обратный или дополнительный код и в таком виде хранятся, перемещаются
и участвуют в операциях.При выводе таких чисел из компьютера происходит обратное преобразование в отрицательные десятичные числа.
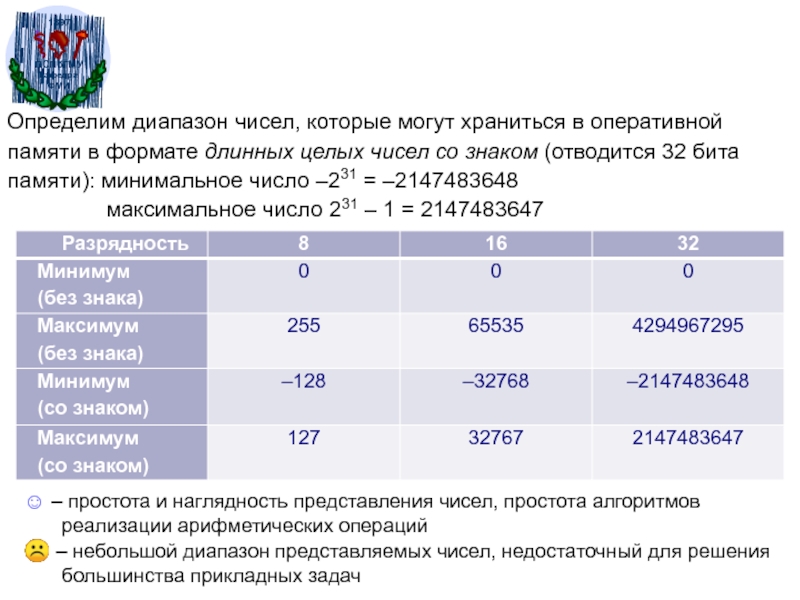
Слайд 37Определим диапазон чисел, которые могут храниться в оперативной памяти в
формате длинных целых чисел со знаком (отводится 32 бита памяти):
минимальное число –231 = –2147483648максимальное число 231 – 1 = 2147483647
– простота и наглядность представления чисел, простота алгоритмов
реализации арифметических операций
– небольшой диапазон представляемых чисел, недостаточный для решения
большинства прикладных задач
Слайд 38Представление вещественных чисел
в компьютере
Любое число N в системе счисления
с основанием q можно записать в виде N = m
∙ q p, где m называется мантиссой числа, а р – порядком.Такой способ записи чисел называется представлением числа с плавающей точкой.
Характеристики форматов вещественных чисел
Слайд 39Способ представления числа с плавающей запятой, опирается на нормализованную (экспоненциальную)
запись действительных чисел.
Нормализованной называется запись отличного от нуля действительного числа
в виде m*pq, где q – целое число (положительное, отрицательное или ноль), а m – правильная Р-ичная дробь, у которой первая цифра после запятой не равна нулю. Мантисса нормализованного числа может изменяться в диапазоне: 1/q ≤ | m | < 1. В нормализованных числах цифра после точки всегда должна быть значащей.
Пример: 0,0836*103 = 0,836*102
ненормализованное число
нормализованное число
При этом, часть разрядов отводится для записи порядка числа, а остальные разряды – для записи мантиссы. По одному разряду в каждой группе отводится для изображения знака порядка и знака мантиссы (0 – если знак плюс, 1 – знак минус).
Следующие k-разрядов используются для изображения абсолютной величины порядка числа, остальные n-разрядов используются для изображения абсолютной величины мантиссы.
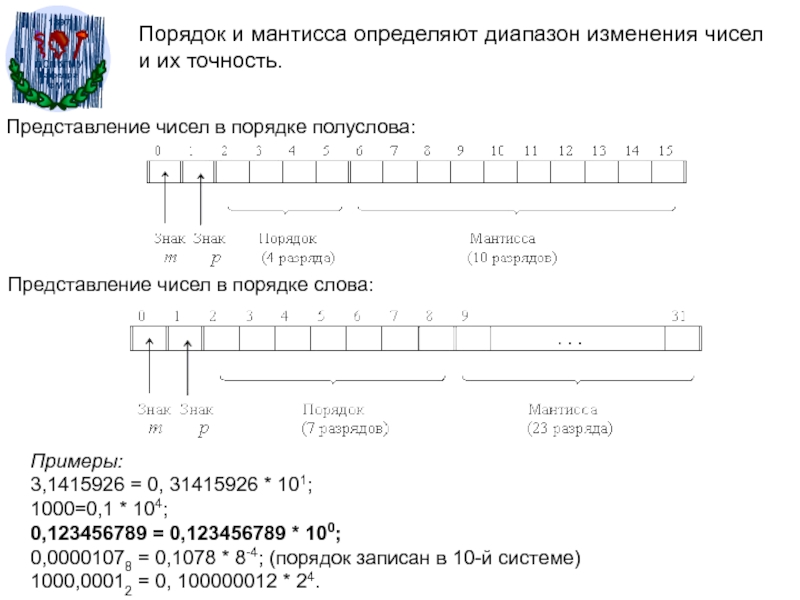
Слайд 40Порядок и мантисса определяют диапазон изменения чисел и их точность.
Представление
чисел в порядке полуслова:
Представление чисел в порядке слова:
Примеры:
3,1415926 = 0,
31415926 * 101;1000=0,1 * 104;
0,123456789 = 0,123456789 * 100;
0,00001078 = 0,1078 * 8-4; (порядок записан в 10-й системе)
1000,00012 = 0, 100000012 * 24.
Слайд 41При записи основания числа в десятичной системе можно говорить о
нормализованной записи: мантиссу и порядок q-ичного числа записывают в системе
счисления с основанием q.Различают:
– научная нормализованная запись числа: 1 ≤ │m│< 10, q = 10, (3,5*102)
– инженерная нормализованная запись (информатика):
0,1< │m│≤ 1, q = 10, (0,35*102)
– компьютерная нормализованная запись: 1 ≤ │m│< 10, q = 10(E), (3,5Е2)
Максимальным числом представимым в формате слова будет A=(0.1111...1·101111111)2 (1·2127)10.
Числа с плавающей точкой позволяют увеличить диапазон обрабатываемых чисел, но при этом точность изображения чисел определяется только разрядами мантиссы и уменьшается по сравнению с числами с фиксированной точкой. Точность может быть повышена путем увеличения количества разрядов мантиссы. Это реализуется путем представления чисел с так называемой двойной точностью (используется формат двойного слова).
Слайд 42Выполнение арифметических операций
над числами с плавающей запятой
При сложении и
вычитании чисел – производится выравнивание порядка. После этой операции одинаковые
разряды чисел оказываются расположенными в одних и тех же по номеру разрядах ячеек, отведенных под операнды, и теперь уже сложение или вычитание мантисс выполняется достаточно просто, так же, как над целыми числами.102*0,23619
10-2*0,71824, меньший порядок «приводится» к большему
102*0,23619
102*0,00071824
102*0,23690824
При умножении двух целых чисел с плавающей запятой их порядки необходимо просто сложить, а мантиссы – перемножить без предварительного выравнивания.
При делении из порядка делимого надо вычесть порядок делителя, а мантиссу делимого разделить на мантиссу делителя.
+
+
Слайд 43В 1976 г. была принята инициатива создать единый стандарт для
представления чисел с плавающей запятой.
Свои предложения по единому стандарту
представили компании DEC, National Superconductor, Zilog, Motorola. Разработчики «K-C-S» победили и их детище воплотилось в стандарт IEEE754. Числа с плавающей запятой в нем представлены в виде знака (s), мантиссы (M) и порядка (E) следующим образом: (-1)s × 1.M × 2E
Слайд 44IEEE 754 - стандарт двоичной арифметики
с плавающей точкой
Данный стандарт
разработан ассоциацией IEEE (Institute of Electrical and Electronics Engineers) и
используется для представления действительных чисел (чисел с плавающей точкой) в двоичном коде.Наиболее используемый стандарт для вычислений с плавающей точкой, используется многими микропроцессорами и логическими устройствами, а также программными средствами.
Полное название стандарта в ассоциации IEEE:
IEEE Standard for Binary Floating-Point Arithmetic (ANSI/IEEE Std 754-1985)
IEEE стандарт для двоичной арифметики с плавающей точкой (ANSI/IEEE Std 754-1985)
Название стандарта в международной электротехнической комиссии IEC:
IEC 60559:1989, Binary floating-point arithmetic for microprocessor systems
IEC 60559:1989 двоичная арифметика с плавающей точкой для микропроцессорных систем
Стандарт содержит 23 страницы текста в 7 секциях и одном приложении.
Слайд 45В IEEE754 число «0» представляется значением с порядком, равным E=Emin-1
(для single это -127) и нулевой мантиссой. Бесконечности представлены как
числа с порядком E=Emax+1 и нулевой мантиссой. Получить бесконечность можно при переполнении и при делении ненулевого числа на ноль. Бесконечность при делении определили исходя из существования пределов, когда делимое и делитель стремиться к какому-то числу. Соответственно, c/0==±∞ (например, 3/0=+∞, а -3/0=-∞), так как если делимое стремиться к константе, а делитель к нулю, предел равен бесконечности.При 0/0 предел не существует, поэтому результатом будет неопределенность. Неопределенность или NaN (от not a number) – это представление, придуманное для того, чтобы арифметическая операция могла всегда вернуть какое-то не бессмысленное значение. NaN представлен как число, в котором E=Emax+1, а мантисса не нулевая. Любая операция с NaN возвращает NaN.
Специальные числа: ноль, бесконечность и неопределенность
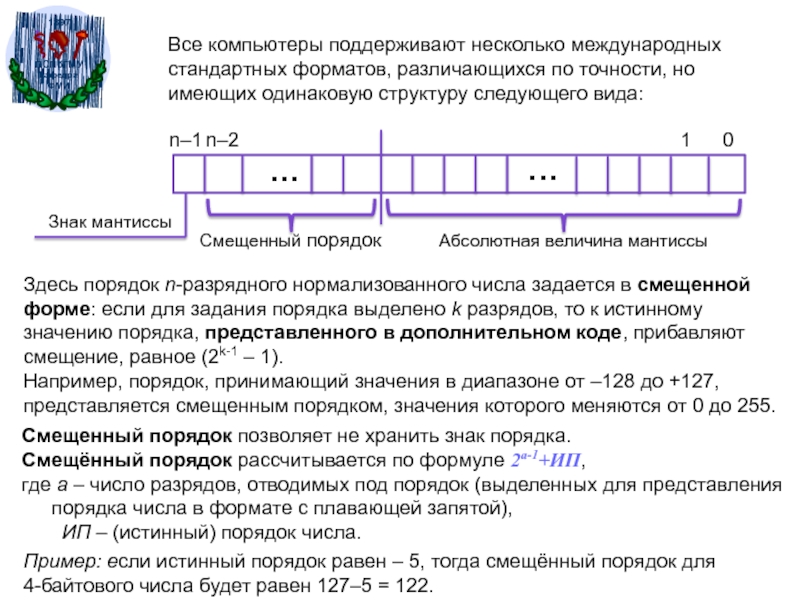
Слайд 46Все компьютеры поддерживают несколько международных стандартных форматов, различающихся по точности,
но имеющих одинаковую структуру следующего вида:
Смещенный порядок
…
…
Абсолютная величина мантиссы
Здесь порядок n-разрядного
нормализованного числа задается в смещенной форме: если для задания порядка выделено k разрядов, то к истинному значению порядка, представленного в дополнительном коде, прибавляют смещение, равное (2k-1 – 1). Например, порядок, принимающий значения в диапазоне от –128 до +127, представляется смещенным порядком, значения которого меняются от 0 до 255.
Смещенный порядок позволяет не хранить знак порядка.
Смещённый порядок рассчитывается по формуле 2a-1+ИП,
где a – число разрядов, отводимых под порядок (выделенных для представления порядка числа в формате с плавающей запятой),
ИП – (истинный) порядок числа.
Пример: если истинный порядок равен – 5, тогда смещённый порядок для
4-байтового числа будет равен 127–5 = 122.
Слайд 47В компьютере, число с плавающей запятой представляется в виде набора
отдельных двоичных разрядов, условно разделенных на знак, порядок и мантиссу.
Прибавление смещения позволяет
записывать положительные иотрицательные порядки в виде положительных чисел.
Рассмотрим пример записи числа с плавающей точкой:
► число +178.25
► в двоичной системе счисления +1011 0010.01=+1.0110 0100 1 х 2111
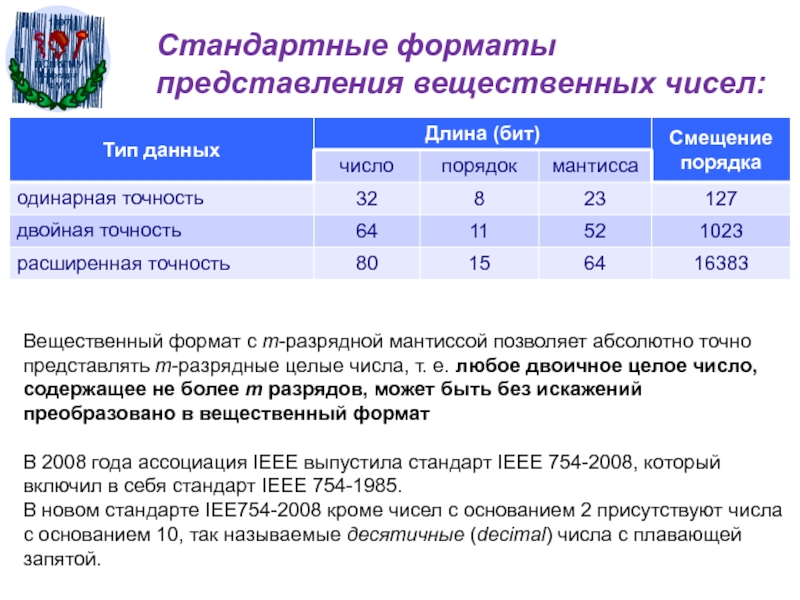
Слайд 48Стандартные форматы представления вещественных чисел:
Вещественный формат с m-разрядной мантиссой позволяет абсолютно
точно представлять m-разрядные целые числа, т. е. любое двоичное целое число, содержащее
не более m разрядов, может быть без искажений преобразовано в вещественный форматВ 2008 года ассоциация IEEE выпустила стандарт IEEE 754-2008, который включил в себя стандарт IEEE 754-1985.
В новом стандарте IEE754-2008 кроме чисел с основанием 2 присутствуют числа с основанием 10, так называемые десятичные (decimal) числа с плавающей запятой.
Слайд 49Алгоритм представления числа
с плавающей запятой
Перевести число из p-ичной системы
счисления в двоичную;
представить двоичное число в нормализованной экспоненциальной форме;
рассчитать смещённый
порядок числа;разместить знак, порядок и мантиссу в соответствующие разряды сетки.
Слайд 50Пример
Представить число -25,625 в машинном виде с использованием 4 байтового
представления (где 1 бит отводится под знак числа, 8 бит
- под смещённый порядок, остальные биты - под мантиссу).1. 2510=110012 0,62510=0,1012 -25,62510= -11001,1012 2. -11001,1012 = -1,10011012 * 24 3. СП=127+4=131 4.
Окончательный ответ: C1CD0000
Слайд 51Информация почти всегда является ответом. Наиболее простые вопросы те, на
которые можно дать ответы «ДА» или «НЕТ».
В кибернетике и информатике
за единицу информации принято считать такое количество информации, при котором из двух равновероятных возможностей можно выбрать одну. Такая единица информации называется БИТ.Количество информации, которое необходимо для получения ответа при выборе из нескольких возможностей, равно логарифму по основанию 2 от числа возможностей. Один бит информации равен Log22 = 1.
Единицы измерения объема информации:
1 байт = 8 бит
1 килобайт = 1024 байт
1 мегабайт = 1024 килобайта
1 гигабайт = 1024 мегабайта
1 терабайт = 1024 гигабайт = 240 байт (примерно 1012 байт), иногда называют тонна.
1 петабайт = 1024 терабайт = 250 байт (примерно 1015 байт)
1 эксабайт = 1024 петабайт = 260 байт примерно 1018 байт)
1 зеттабайт = 1024 эксабайт = 270 байт (примерно 1021 байт)
1 йоттабайт = 1024 зеттабайт = 280 байт (примерно 1024 байт) и т.д.
Слайд 52Кодирование текстовой информации
Соответствие между набором символов и набором числовых значений
называется кодировкой символа. При вводе в компьютер текстовой информации происходит
ее двоичное кодирование. Код символа хранится в оперативной памяти компьютера. В процессе вывода символа производится обратная операция – декодирование, т.е.преобразование символа в его изображение.Институтом стандартизации США была введена в действие система кодирования ASCII (American Standard Code for Information Interchange). Каждому символу ASCII соответствует 8–битовый двоичный код
(1 символ – 1 байт).
В последнее время широкое распространение получил новый международный стандарт Unicode. Стандарт состоит из двух основных разделов: универсальный набор символов (UCS, universal character set) и семейство кодировок (UTF, Unicode transformation format).
Каждому символу Unicode соответствует 16–битовый двоичный код
(1 символ – 2 байта).
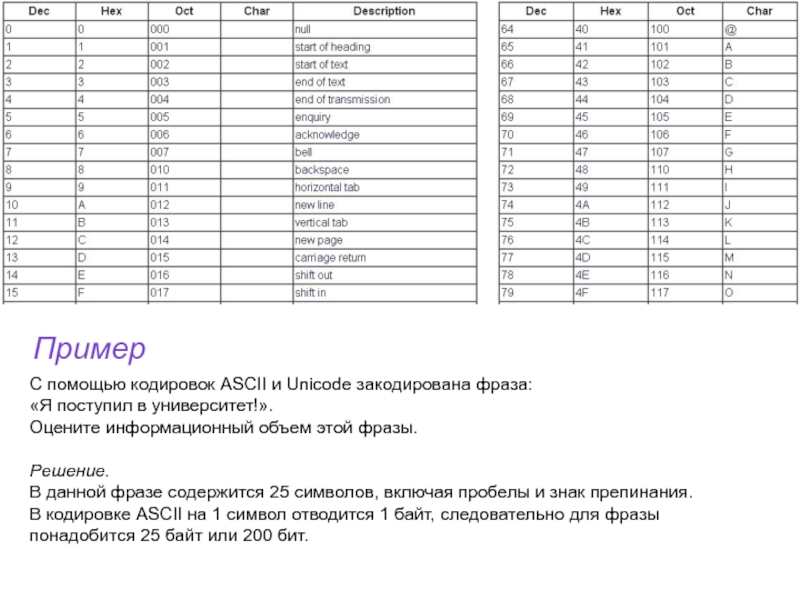
Слайд 53Пример
С помощью кодировок ASCII и Unicode закодирована фраза:
«Я поступил в
университет!».
Оцените информационный объем этой фразы.
Решение.
В данной фразе содержится 25
символов, включая пробелы и знак препинания. В кодировке ASCII на 1 символ отводится 1 байт, следовательно для фразы понадобится 25 байт или 200 бит.
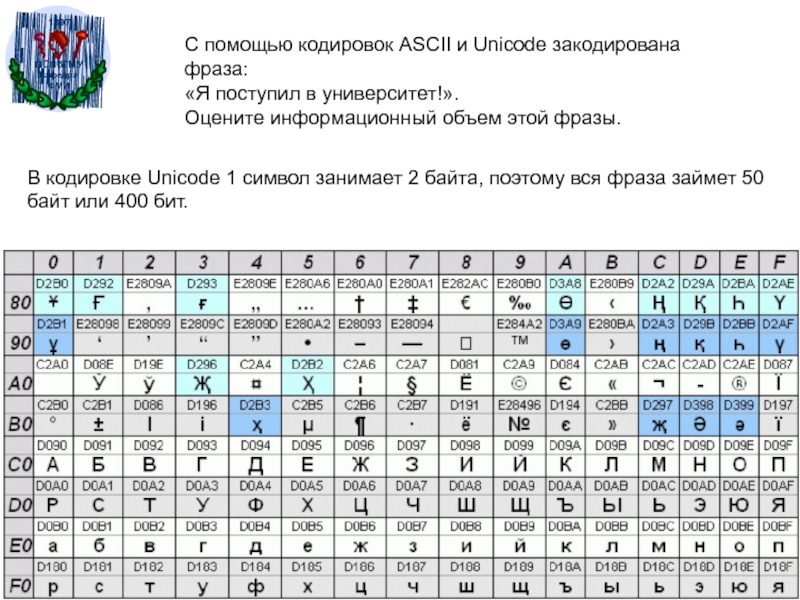
Слайд 54С помощью кодировок ASCII и Unicode закодирована фраза:
«Я поступил в
университет!».
Оцените информационный объем этой фразы.
В кодировке Unicode 1 символ
занимает 2 байта, поэтому вся фраза займет 50 байт или 400 бит.Слайд 55Формула Хартли
Для измерения количества информации, которое может быть передано при
помощи алфавита, существует формула Хартли
n = pi ,
где n – число равновероятных событий, i – количество информации, полученной в результате совершения события,
p – количество различных вариантовили
p – количество используемых символов, i – длина строки символов или сигналов.
Пример:
Сколько различных сигналов можно записать с помощью 32-разрядного компьютерного кода. В этом случае длина строки – 32, количество используемых символов – 2, следовательно n = 232 = 4 294 967 296.
Слайд 57В текстовом режиме экран разбивается на 25 строк по 80
символов. Каждая позиция экрана называется знакоместом, в нем находится один
символ. Символ может быть высвечен одним из 16 цветов, можно изменять и цвет фона (8 цветов). Для описания каждого знакоместа потребуется 2 байта: 1 байт – символ, 2 байт – его цветовые характеристики (цвет символа 4 бита, цвет фона 3 бита и 1 бит для представления мерцания (0 – не мерцает, 1 – мерцает). Таким образом содержимое экрана занимает в видеопамяти компьютера 25*80*2=4000 байт = 4 Кбайта.В графическом режиме экран разделяется по пиксели, количество которых определяет разрешающую способность монитора и зависит от его типа и режима. Такая форма представления информации называется растровой. Каждый пиксель может иметь цвет (16, 256, 16000 и т д.), 256 цветов – 1 байт. При объемном характере растра ячейка называется вокселем: образовано из слов: объёмный (англ. volumetric) и пиксел ( англ. pixel), содержит значение элемента растра в трехмерном пространстве. Трёхмерная матрица хранит значение
воксела для каждого единичного элемента объёмного
пространства, поэтому воксельные модели хорошо подходят
для моделирования. Для воксельных моделей существует
множество алгоритмов визуализации.
Мониторы могут работать в двух режимах: текстовом и графическом.
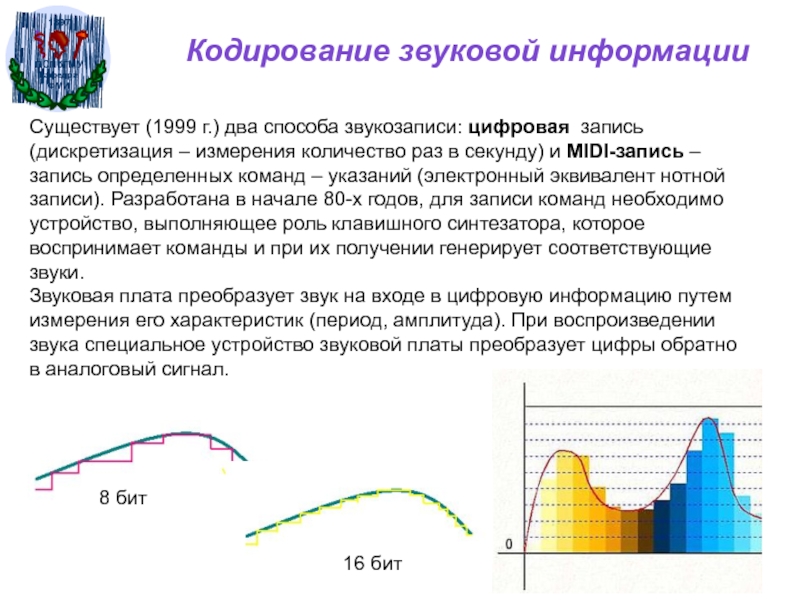
Слайд 58Кодирование звуковой информации
Существует (1999 г.) два способа звукозаписи: цифровая запись
(дискретизация – измерения количество раз в секунду) и MIDI-запись –
запись определенных команд – указаний (электронный эквивалент нотной записи). Разработана в начале 80-х годов, для записи команд необходимо устройство, выполняющее роль клавишного синтезатора, которое воспринимает команды и при их получении генерирует соответствующие звуки.Звуковая плата преобразует звук на входе в цифровую информацию путем измерения его характеристик (период, амплитуда). При воспроизведении звука специальное устройство звуковой платы преобразует цифры обратно в аналоговый сигнал.
8 бит
16 бит
Слайд 59Аналоговый сигнал
КВАНТОВАНИЕ
ДИСКРЕТИЗАЦИЯ
Интервал дискретизации
1 1 1
1 1 0
1 0 1
1 0
0
0 1 1
0 1 0
0 0 1
0 0 0
УРОВЕНЬ
КВАНТОВАНИЯ
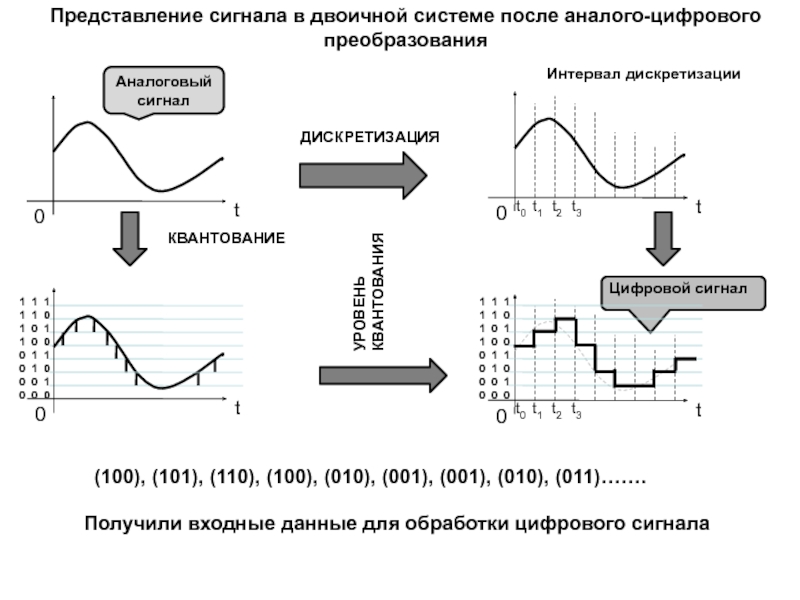
Представление сигнала
в двоичной системе после аналого-цифрового преобразования(100), (101), (110), (100), (010), (001), (001), (010), (011)…….
Получили входные данные для обработки цифрового сигнала
0
t
t0
t1
t2
t3
t0
t1
t2
t3
1 1 1
1 1 0
1 0 1
1 0 0
0 1 1
0 1 0
0 0 1
0 0 0
Слайд 60КОНТРОЛЬНЫЕ ВОПРОСЫ:
Перечислите типы систем счисления.
Что является основанием системы счисления, перечислите
алфавит нескольких систем счисления.
Укажите представление числа в позиционной системе счисления.
Опишите
алгоритм перевода целых чисел в другую систему счисления.Опишите алгоритм перевода дробных чисел в другую систему счисления.
Перечислите и приведите примеры арифметических операций в позиционных системах счисления.
Укажите правила хранения целых и вещественных чисел в компьютере.
Что такое прямой, обратный и дополнительный код?
Что такое нормализованная запись числа?
Приведите алгоритм выполнения арифметических операций над числами с плавающей запятой.
Перечислите стандартные форматы представления вещественных чисел.
Приведите пример перевода числа с плавающей запятой в машинный формат.
Перечислите виды кодирования текстовой информации.
Опишите виды кодирования графической информации в компьютере.
Укажите алгоритм кодирования звуковой информации в компьютере.
/74
Спасибо за внимание !!!