Слайд 1Теоретические основы систем автоматизированного проектирования
Слайд 2Лекция 1Лекция 1 Лекция 10Лекция 1 Лекция 10 Лекция 19
Лекция
2Лекция 2 Лекция 11Лекция 2 Лекция 11 Лекция 20
Лекция 3Лекция
3 Лекция 12Лекция 3 Лекция 12 Лекция 21
Лекция 4Лекция 4 Лекция 13Лекция 4 Лекция 13 Лекция 22
Лекция 5Лекция 5 Лекция 14Лекция 5 Лекция 14 Лекция 23
Лекция 6 Лекция 6 Лекция 15Лекция 6 Лекция 15 Лекция 24
Лекция 7Лекция 7 Лекция 16Лекция 7 Лекция 16 Лекция 25
Лекция 8Лекция 8 Лекция 17
Лекция 9Лекция 9 Лекция 18
Слайд 3Учебно-методические материалы
1.Норенков И.П. Основы автоматизированного проектирования. М.: Изд-во МГТУ им.
Н.Э.Баумана, 2000.
2.Автоматизация проектирования радиоэлектронных средств. Под ред. О.В. Алексеева. М.:
Высшая школа, 2000.
3.Методы оптимизации в примерах и задачах: Учебное пособие / А. В. Пантелеев, Т. А. Летова. - 3-е издание - М.: Высшая школа, 2008.
4.Зарубин В.С. Математическое моделирование в технике. М.: МГТУ им Баумана, 2001.
8. Деньдобренько Б.Н., Малика А.С. Автоматизация конструирования РЭА. М. Высш. школа, 1980.
Слайд 4В результате изучения дисциплины студенты должны:
знать:
основные понятия теории САПР;
методологию автоматизированного проектирования ЭВС;
методы формального описания основных объектов проектирования;
методы анализа
и синтеза подсистем ЭВС;
основы теории систем массового обслуживания;
элементы численных методов;
модели данных в САПР;
основные методы и алгоритмы, реализуемые САПР ЭВС;
Слайд 5уметь:
выбирать и строить математические модели объектов проектирования;
выбирать и использовать методы
оптимизации при проектировании ЭВС;
моделировать информационные и физические процессы, протекающие в
ЭВС;
приобрести навыки:
математического моделирования при проектировании ЭВС;
практического использования методов и алгоритмов, реализуемых САПР ЭВС.
Слайд 6Лекция 1
Основные понятия теории САПР
Слайд 7Основные понятия теории САПР
Проектирование – это процесс, заключающийся в преобразовании
исходного описания объекта в окончательное описание на основе выполнения комплекса
работ исследовательского, расчетного и конструкторского характера.
Проектирование, при котором все или часть проектных решений получают путем взаимодействия человека и ЭВМ, называют автоматизированным. Система, реализующая автоматизированное проектирование и представляет собой САПР.
Слайд 8Типовые проектные процедуры
Преобразовании исходного описания объекта проектирования в окончательное порождает
промежуточные описания, которые называют проектными решениями. Эти преобразования реализуются при
использовании проектных процедур.
Различают проектные процедуры анализа и синтеза. Синтез заключается в создании описания объекта, а анализ – в определении свойств и исследовании работоспособности объекта по его описанию, т.е. при синтезе создаются, а при анализе оцениваются проекты объектов.
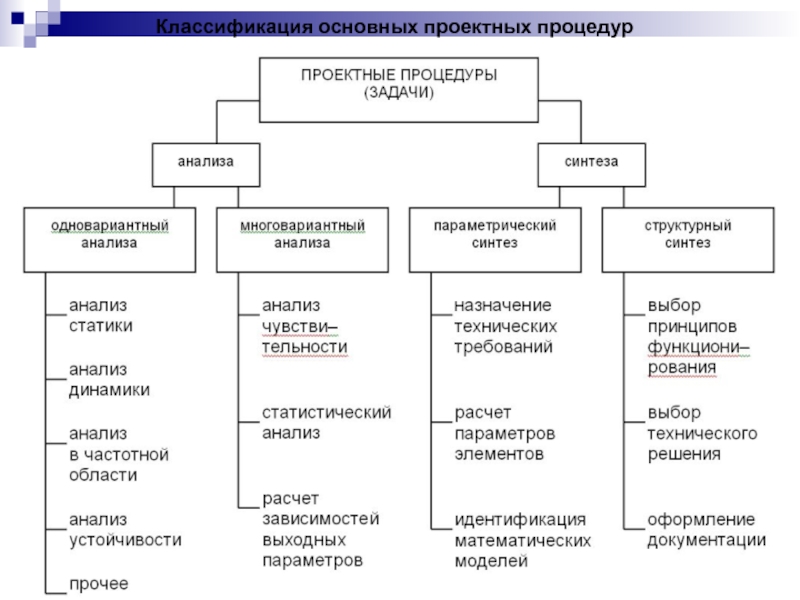
Слайд 9Классификация основных проектных процедур
Слайд 10Иерархические уровни проектирования
Системный уровень, на котором решаются наиболее общие задачи
проектирования. В этом случае результаты проектирования представляются в виде структурных
схем, укрупненных алгоритмов работы, диаграмм потоков данных, диаграмм организации вычислительных процессов и т.п.
Макроуровень, на котором проектируются отдельные устройства и узлы ЭВС. Результаты проектирования представляются в виде функциональных, принципиальных схем, сборочных чертежей и т.п. Макроуровень также называют схемотехническим уровнем.
Микроуровень, на котором проектируются отдельные детали и элементы ЭВС.
При проектировании цифровых систем часто также выделяют функционально-логический уровень, на котором модель цифрового устройства представляется в виде системы логических уравнений, описывающих логику функционирования элементов цифрового устройства.
Слайд 11CAD CAM CAE системы
CAD-системы (сomputer-aided design — компьютерная поддержка проектирования)
предназначены для решения конструкторских задач и оформления конструкторской документации
CAM-системы
(computer-aided manufacturing — компьютерная поддержка производства) предназначены для проектирования обработки изделий на станках с числовым программным управлением (ЧПУ) и выдачи программ для этих станков
САЕ-системы — (computer-aided engineering — поддержка инженерных расчетов)
Слайд 12Основные задачи, решаемые CAD – CAM – CAE системами при
проектировании ЭВС:
Проектирование печатных плат.
Оформление конструкторской документации.
Моделирование работы аналоговых и цифровых,
а также смешанных аналого-цифровых устройств. В отношении моделирования работы устройств используется термин simulation (симулирование).
Синтез цифровых устройств на ПЛИС и моделирование их работы.
Анализ электромагнитной совместимости.
Тепловое моделирование.
Проектирование топологии БИС.
Схемотехническое и электромагнитное моделирование СВЧ устройств.
Поведенческое моделирование на уровне структурных схем.
Подготовка файлов для станков с ЧПУ и фотоплоттеров.
Слайд 13Виды обеспечения автоматизированного проектирования
Техническое обеспечение САПР представляет собой совокупность взаимосвязанных
и взаимодействующих технических средств, предназначенных для выполнения автоматизированного проектирования (hardware).
Структура автоматизированного рабочего места
Слайд 14Математическое обеспечение САПР объединяет в себе математические модели проектируемых объектов,
методы и алгоритмы выполнения проектных процедур, используемые при
автоматизированном проектировании.
Программное обеспечение САПР объединяет собственно программы и программную документацию, необходимую для эксплуатации программы.
Информационное обеспечение САПР объединяет всевозможные данные, необходимые для выполнения автоматизированного проектирования.
Лингвистическое обеспечение САПР представлено совокупностью языков, применяемых для описания процедур автоматизированного проектирования и проектных решений.
Методическое обеспечение САПР составляют документы, характеризующие состав, правила отбора и эксплуатации средств автоматизированного проектирования.
Слайд 15Лекция 2
Системный подход к проектированию ЭВС. Иерархия и классификация математических
моделей.
Слайд 16Системотехника – дисциплина, в которой исследуется процесс проектирования технических систем.
Система
– множество элементов, находящихся в отношениях и связях между собой.
Элемент
– такая часть системы, представление о которой нецелесообразно подвергать дальнейшему членению при проектировании
Подсистема – часть системы, которая имеет свойства системы (большого количества элементов с большим числом взаимосвязей).
Слайд 17Параметр(переменная) – величина, выражающая свойство системы или ее части. Параметры
подразделяются на внешние внутренние и выходные. Векторы внутренних, выходных и
внешних параметров будем обозначать X = (x1, x2, ….xn) ,
Y = (y1, y2, ….ym), Q = (q1, q2, ….qk).
Фазовая переменная - величина, характеризующая энергетическое или информационное наполнение подсистемы или элемента, но не являющаяся внутренним параметром (внутренний параметр – номинал, фазовые переменные – падение напряжения и ток). Вектор фазовых переменных будем обозначать V=(v1, v2, ..vl).
Состояние – совокупность значений фазовых переменных для определенного момента времени.
Слайд 18Формы представления математических моделей.
Инвариантная форма - запись соотношений модели
с помощью математического языка безотносительно к методу решения уравнений модели.
Алгоритмическая
форма - запись соотношений модели и выбранного численного метода решения в форме алгоритма.
Аналитическая форма - запись модели в виде результата аналитического решения исходных уравнений модели. Обычно модели в аналитической форме представляют собой явные выражения выходных параметров как функций внешних и внутренних параметров.
Схемная форма, называемая также графической формой - представление модели на некотором графическом языке, например на языке графов, диаграмм, эквивалентных схем и т.п.
Слайд 19Требования к математическим моделям.
1) требование адекватности. Модель считается адекватной, если
отражает заданные свойства объекта с приемлемой точностью. Точность определяется как
степень совпадения значений выходных параметров модели и объекта;
2) модель должна иметь однозначное соответствие между параметрами и физическими процессами в ЭВС;
3) модель должна быть пригодна для обработки на ЭВМ;
4) модель должна быть экономична. Экономичность модели характеризуется затратами вычислительных ресурсов для ее реализации, т.е. затратами машинного времени и памяти.
Слайд 20Пример математической моделей на микроуровне
Нестационарное уравнение теплопроводности плоской стенки толщиной
h, на поверхности которой, начиная с некоторого момента времени τ=0,
начинает действовать источник теплоты удельной тепловой мощностью q(τ). С другой поверхности стенки тепловой поток рассеивается в окружающую среду с температурой t0 по закону Ньютона при постоянном коэффициенте теплоотдачи. Будем полагать, что теплофизические характеристики не зависят от температуры.
Θ(x, τ)=t(x, τ) - t0
Θ(x,0)=0 ;
Слайд 21Пример модели на макроуровне
Временная зависимость тока, протекающего через
постоянный конденсатор
,
где с – емкость конденсатора,
u – напряжение на конденсаторе,
t – время.
Слайд 22Компонентными уравнениями называют уравнения, описывающие свойства элементов (компонентов), т.е. это
уравнения математических моделей элементов.
Топологическими уравнениями описывают взаимосвязи в составе моделируемой
системы.
Слайд 23Для электрических систем компонентные уравнения простых двухполюсников:
для R: u =
iR (закон Ома),
для L:
,
для С :
,
u
— падение напряжения на двухполюснике, i — ток.
Слайд 24Для электрических систем топологические уравнения выражают законы Кирхгофа
Кp
— множество номеров элементов р-гo контура,
Jq — множество номеров
элементов, входящих в q-e сечение
Слайд 25Пример математической модели
на системном уровне
Анализ персонального компьютера с точки
зрения надежности.
S0 – исправное состояние, S1- неработоспособное состояние,
-
интенсивность потока отказов,
μ - интенсивность потока восстановлений
Уравнение Колмогорова для состояния S0
Слайд 26Лекция 3
Интерполяция табличных данных.
Слайд 27Необходимость интерполяции и аппроксимации функций в основном связана с двумя
причинами:
Функция f(x) имеет сложное аналитическое описание, вызывающее определенные трудности
при его использовании (например, f(x) является специальной функцией: гамма-функцией, эллиптической функцией и др.).
Аналитическое описание функции f(x) неизвестно, т. е. f(x) задана таблично. При этом необходимо иметь аналитическое описание, приближенно представляющее f(x) (например, для вычисления значений f(x) в произвольных точках, определения интегралов и производных от f(x) и т. п.)
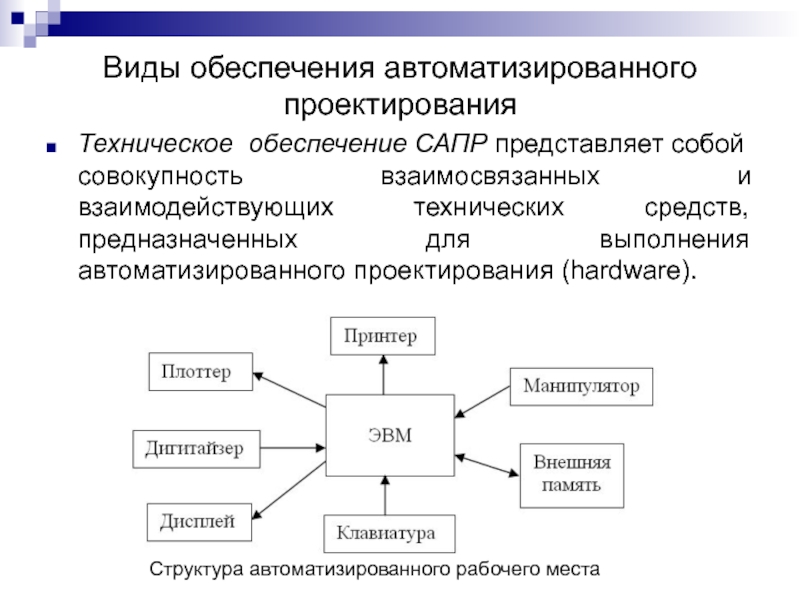
Слайд 28Интерполяция данных
На отрезке [a, b] заданы n + 1 точка xi = х0, х1, . . ., хn,
которые
называются узлами интерполяции, и значения
некоторой функции f(x) в этих
точках
f(x0) = y0, f(x1) = y1, . . ., f(xn) = yn.
Требуется построить функцию ϕ(x) , такую что
ϕ (x0) = y0, ϕ (x1) = y1, . . ., ϕ (xn) = yn.
В качестве интерполирующей функции ищется полином ϕ (х)
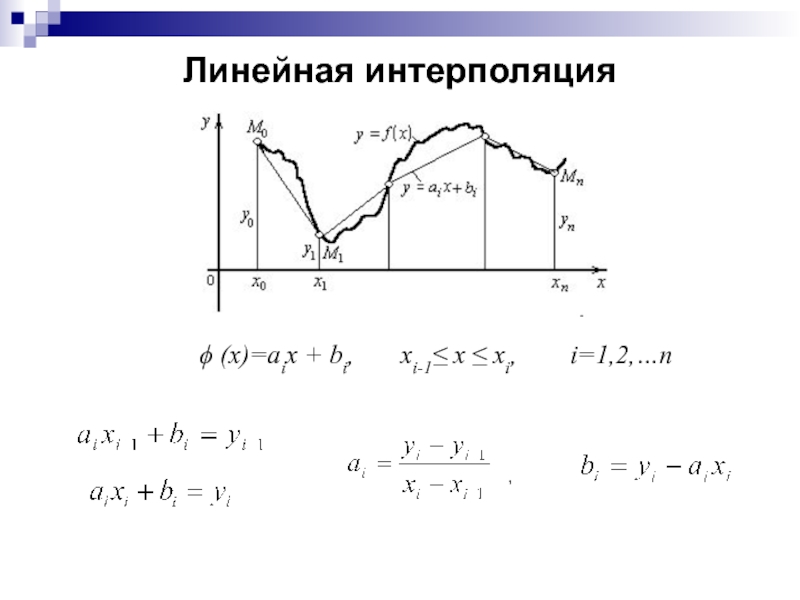
Слайд 29Линейная интерполяция
ϕ (х)=aix + bi, xi-1≤
x ≤ xi, i=1,2,…n
,
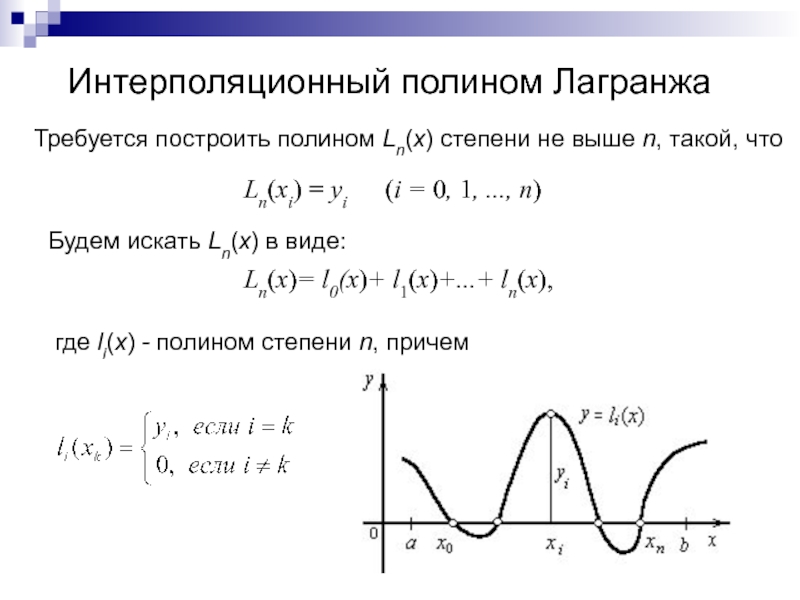
Слайд 30Интерполяционный полином Лагранжа
Требуется построить полином Ln(x) степени не выше n,
тaкой, что
Ln(xi) = yi (i = 0, 1,
..., n)
Будем искать Ln(x) в виде:
Ln(x)= l0(x)+ l1(x)+...+ ln(x),
где li(x) - полином степени n, причем
Слайд 31Так как искомый полином li(x) обращaется в нуль в n
точках,
то он имеет вид
li(x) = Ci (x –
x0) (x - x) … (x - xi-) (x - xi +) ... (x - xn)
где Сi - постоянный коэффициент.
Полагая х = xi и учитывая, что li(xi) = yi, получим
Интерполяционная формула (интерполяционный полином)
Лагранжа.
Слайд 32Пример. Пусть заданы значения x0=1; x1=3; x2=7; x3=12;
и y0=5,6;
y1=6,7; y2=8,1; y3=10,3.
Определить значение неизвестной функции для х = 6,5.
L3(6,5)=7,9
Слайд 33Интерполяционный многочлен Ньютона с разделенными разностями
разделенная разность
первого порядка.
разделенная разность
второго порядка.
Разделенная разность порядка k≥2
Слайд 34Интерполяционный многочлен Ньютона
Пример. Необходимо построить интерполяционный
многочлен Ньютона:
Слайд 35Таблица разделенных разностей
Интерполяционный многочлен Ньютона:
Слайд 36Погрешность полиномиальной интерполяции
Предположим, что во всех точках х∈[a, b] функция f(x)
имеет (n+1) непрерывную производную.
Тогда абсолютная ошибка интерполяции
ε(x)=| f(x)– Pn(x) | определяется
выражением
где
- максимальное значение (n+1)-й производной
функции f(x) на интервале [a, b]; hmax=max hi , hi=xi - xi-1.
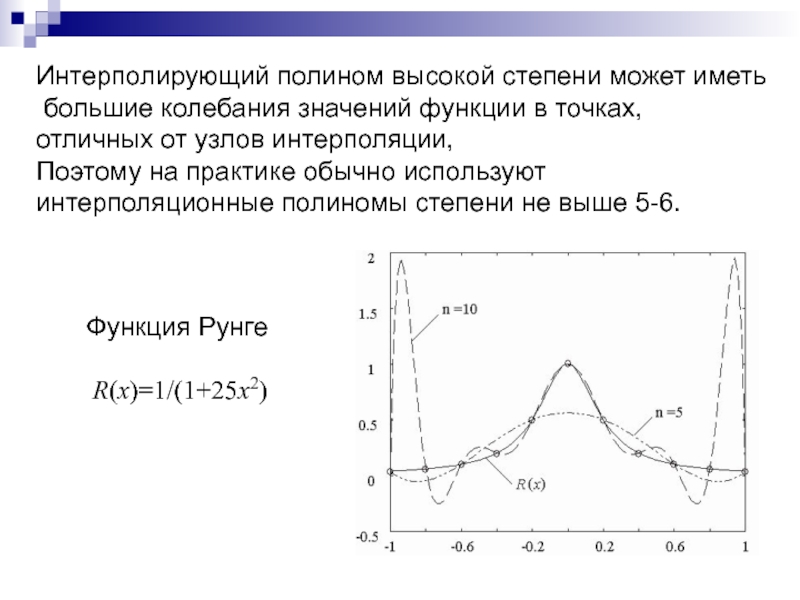
Слайд 37Интерполирующий полином высокой степени может иметь
большие колебания значений функции
в точках,
отличных от узлов интерполяции,
Поэтому на практике обычно
используют
интерполяционные полиномы степени не выше 5-6.
R(x)=1/(1+25x2)
Функция Рунге
Слайд 38Пример. Пусть требуется составить таблицу функции y=ln x на отрезке
[1,10]. Какой величины должен быть шаг h, чтобы при линейной
интерполяции значение функции восстанавливалось с погрешностью не более ε=10-2?
Запишем остаточный член интерполяции при линейной интерполяции
Тогда h2≤8⋅10-2. Следовательно, h<0,3.
Так как
то
Слайд 39Сплайн - интерполяция
На практике чаще всего используют кубический сплайн.
Для
получения расчетных выражений коэффициентов сплайна
дополнительно накладывается ограничение совпадения первых
и вторых производных в узлах интерполяции. Для n интервалов
интерполяции необходимо составление 4n уравнений для
определения неизвестных коэффициентов:
1
Слайд 40В случае задания в начальном узле интерполяции значений
первой и
второй производной для кубического сплайна их
коэффициенты могут быть получены
по следующим
рекуррентным выражениям:
Для первого интервала
,
,
,
,
где значения
должны быть заданы.
и
Слайд 41Для последующих i-ых интервалов
,
,
,
где
,
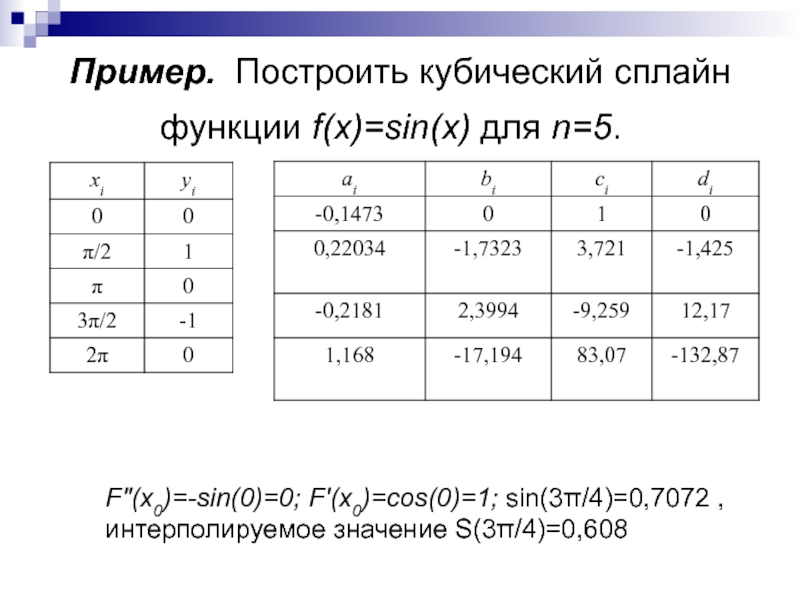
Слайд 42Пример. Построить кубический сплайн функции f(x)=sin(x) для n=5.
F"(x0)=-sin(0)=0; F'(x0)=cos(0)=1; sin(3π/4)=0,7072
,
интерполируемое значение S(3π/4)=0,608
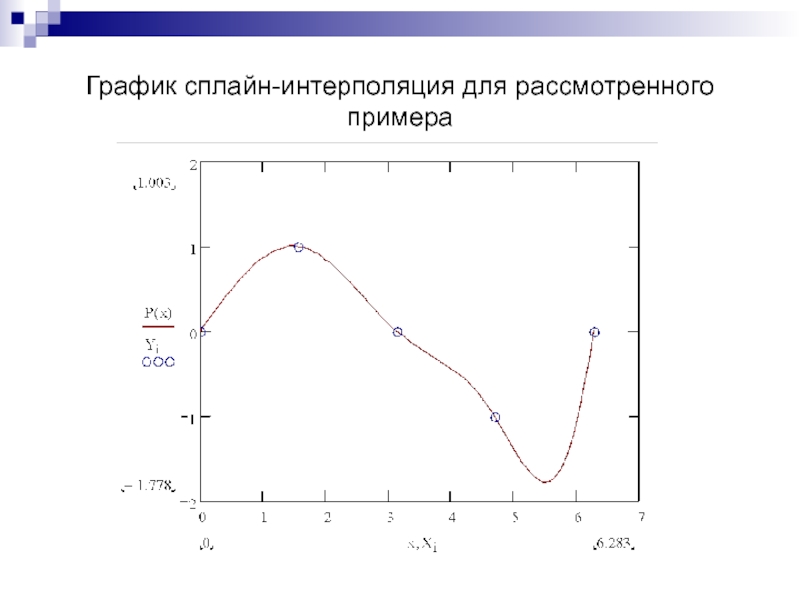
Слайд 43График сплайн-интерполяция для рассмотренного примера
Слайд 44Лекция 4
Аппроксимация табличных данных и функций.
Численное решение систем линейных
уравнений
Слайд 45Аппроксимация
Наиболее распространенным методом аппроксимации данных является метод наименьших квадратов.
Критерием
близости в методе наименьших квадратов
является требование минимальности
среднего квадратического
отклонения
Пусть функция y=f(x) задана таблицей своих значений:
yi=f(xi), i=0,1, ..n.
Слайд 46Критерий близости записывается в следующем виде
В отличие от задачи интерполяции
не требуется,
чтобы аппроксимирующая функция проходила через все
заданные точки.
Наиболее
часто встречаются аппроксимация прямой линией
(линейная регрессия), аппроксимация полиномом
(полиномиальная регрессия), аппроксимация линейной
комбинацией произвольных функций.
Слайд 47Аппроксимация прямой
Из всех прямых ϕ (x) = ax + b
выбирается та,
для которой сумма квадратов отклонений
значений функции от
этой прямой минимальна.
Слайд 49Аппроксимация полиномом с помощью МНК
Требуется найти полином фиксированной степени
m,
для которого СКО
минимально.
Слайд 50Нормальная система уравнений МНК
, k=0,1,..m.
Полученная
система есть система линейных
алгебраических уравнений относительно
неизвестных a0,a1,a2….am.
Используя
необходимое условие экстремума, получим
Слайд 51Нормальная система для полинома второй степени P2(x)=a0+a1x+a2x2
Слайд 52Пример. Осуществим аппроксимацию табличных данных
полиномом второй степени.
Вычислим коэффициенты нормальной
системы уравнений:
,
,
Слайд 53Нормальная система будет иметь вид:
Решение системы: a0=1,234; a1=0,98;
a2=-0,279.
P2(x)=1,234+0,98x-0,279x2.
Слайд 54Пример. Выведем систему уравнений для определения коэффициентов a и b
функции
осуществляющей среднеквадратичную аппроксимацию заданной функции по n+1 точке
Минимизируемая функция
Слайд 55условие экстремума
нормальная система
Слайд 56Решение систем линейных
алгебраических уравнений.
Способы решения систем линейных уравнений делятся
на две группы:
Точные методы, представляющие собой алгоритмы
для вычисления
корней системы (решение систем с помощью
обратной матрицы, правило Крамера, метод Гаусса и др.),
Итерационные методы, позволяющие получить решение
системы с заданной точностью путем сходящихся
итерационных процессов (метод итерации,
метод Зейделя и др.).
Слайд 57Метод Гаусса
представляют в виде матрицы
Систему уравнений
Слайд 58
которую последовательным исключением неизвестных
приводят к эквивалентной системе с треугольной
матрицей вида
Слайд 59Эта процедура называется прямой ход.
Все коэффициенты (включая d) на
каждом
шаге прямого хода пересчитываются по формулам
,
di=ci(n+1)
где k – индекс исключаемой неизвестной xk
из системы уравнений.
При обратном ходе последовательно вычисляются
неизвестные, начиная с xn.
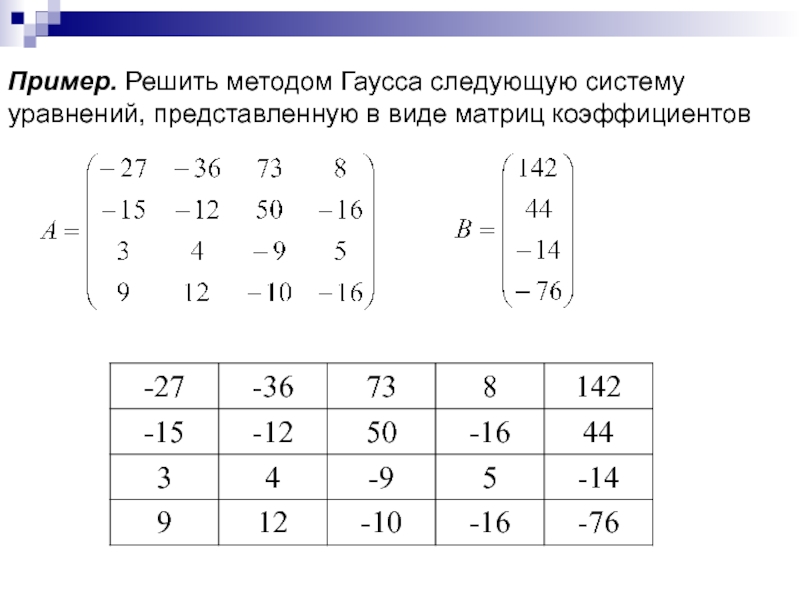
Слайд 60
Пример. Решить методом Гаусса следующую систему
уравнений, представленную в виде матриц коэффициентов
Слайд 611 шаг прямого хода. Из второго-четвертого уравнений исключаем x1
;
Слайд 622 шаг. Исключаем из третьего и четвертого уравнений x2.
Поскольку
с32 и с42 равны нулю, то матрица на этом шаге
не изменится.
3 шаг. Исключаем x3 из четвертого уравнения
Слайд 63Из последней строки находим x4=0
Из третьей строки
Обратный ход
Из второй строки
Из первой строки
Слайд 64Лекция 5
Численное решение нелинейных уравнений
Слайд 65Численное решение нелинейных уравнений.
Решение нелинейного уравнения f(x)=0 или
системы нелинейных
уравнений состоит из двух
этапов:
Отделение корней, то есть отыскание
достаточно малых областей, в каждой из которых
заключен ровно один корень уравнения или
системы уравнений.
2) Вычисление каждого отделенного корня с
заданной точностью.
Слайд 66Итерационный алгоритм отделения корня
Для начального приближения x0, найти f0=f(x0),
задать начальный интервал поиска D и его коэффициент
расширения d
>1.
2. Вычислить a=x0 - D, b=x0+D.
3. Увеличить интервал поиска: D=D*d.
Если интервал превысил некоторый заданный предел
закончить поиск (интервал не найден).
4a. Если знаки fa и f0 отличаются, то считать корень
окруженным на [a,x0] и выйти из алгоритма.
4b. Если знаки fb и f0 отличаются, то считать корень
окруженным на [x0,b] и выйти из алгоритма.
4c. Если f0>0 (случай меньше нуля анализируется
аналогично) перейти к 5.
Слайд 67Продолжение алгоритма отделения корня
5. Проверяется, какое значение из fa или
fb является меньшим.
Если оба одинаковы, то переходим к 6a
(двусторонний поиск),
если fb - производим поиск вправо 6b, иначе - поиск влево 6c.
6a. Находим a=a-D, b=b+D, fa=f(a), fb=f(b), перейти к 3.
6b. Присваиваем последовательно a=x0, x0=b, fa=f0, f0=fb;
находим b=b+D, fb=f(b), перейти к 3.
6c. Аналогично 6b, только направление поиска - влево.
Так как интервал поиска постоянно расширяется,
то в конце концов используя указанный алгоритм корень
будет локализован.
Слайд 68Метод бисекции
Пусть [a,b] - отрезок локализации.
Предположим, что функция f(x)
непрерывна на [a,b]
и на концах принимает значения разных знаков.
Алгоритм метода бисекции состоит в построении
последовательности вложенных отрезков, на концах
которых функция принимает значения разных знаков.
Каждый последующий отрезок получают делением
пополам предыдущего.
Слайд 69Шаг метода бисекции
Пусть на k-ом шаге найден отрезок [ak,bk] такой,
что f(ak)· f(bk)
Если f(xk)=0, то xk - корень и задача решена.
Если нет, то из двух половин отрезка выбираем ту,
на концах которой функция имеет противоположные знаки:
ak+1= ak, bk+1= xk, если f(ak)· f(xk)<0
ak+1= xk, bk+1= bk , если f(ak)· f(xk)>0
Если длина отрезка локализации меньше ε,
то итерации прекращают и в качестве значения
корня с заданной точностью принимают середину отрезка.
Слайд 70Метод Ньютона
Пусть уравнение записано в виде f(x)=0.
Если разложить
f(x) в ряд Тейлора в окрестности
некоторой точки xk и
ограничиться первой производной,
то можно записать
Решение дает очередное приближение к корню
уравнения f(x)=0, которое обозначим как xk+1.
Слайд 71Алгоритм метода Ньютона
Выбираем начальное приближение x0.
Для улучшения сходимости метода
начальное
приближение следует выбирать по возможности ближе
к искомому корню
уравнения.
2. По формуле
рассчитывается значение xk+1
3. Проверяется условие завершения |xk – xk+1|<ε, где
- заранее заданная допустимая погрешность.
Если условие выполняется, то вычислительный процесс
заканчивается, если нет, то переходим к шагу 2.
Слайд 72Пример. Решим методом Ньютона уравнение
x3+2x2+3x+5=0, взяв в качестве
начального
приближения x0=-2 и задав точность ε=0,000001.
Поскольку
то итерационная
формула метода Ньютона будет такой:
,
Применяя эту формулу, последовательно находим:
x1=-1,857143; x2=-1,843842; x3=-1,843734; x4=-1,843734;
Слайд 73Метод может быть использован для случая функции многих
переменных F(X).
В этом случае на втором шаге алгоритма
вычисления для переменной
xj проводятся по выражению
условие завершения
|(xj)k – (xj)k-1|<εj,
εj - заранее заданная допустимая погрешность по переменной xj.
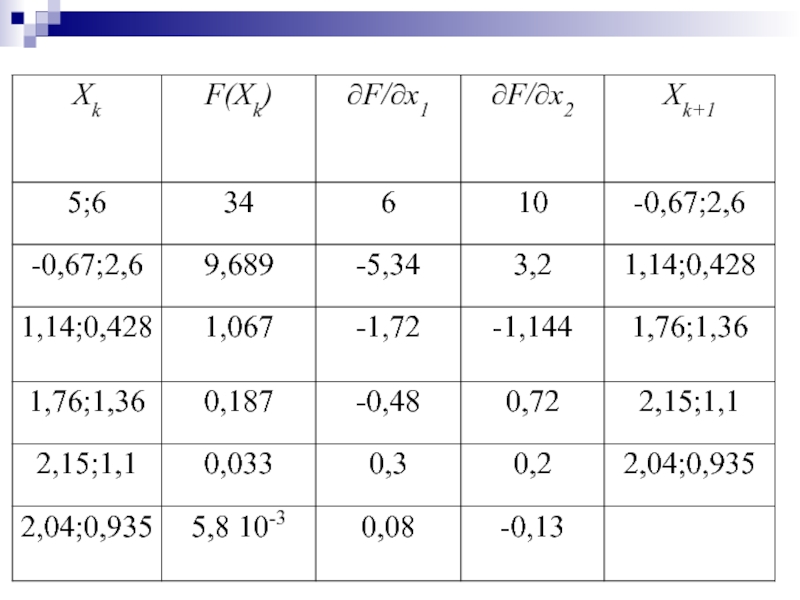
Слайд 74Пример. Найти корень уравнения с точностью ε=0,2
Выберем стартовую точку X0=(5;6)
Слайд 76Численное дифференцирование
По значениям функции f(x) в некоторых узлах x0 ,
x1 , ... , xN строят интерполяционный полином PN(x) и
приближенно полагают
f(r)(x) ≈P(r)N(x), 0 ≤ r ≤ N
Формула численного дифференцирования с остаточным членом
f(r)(x) = P(r)N(x) + R, 0 ≤ r ≤ N
остаточный член R - погрешность численного дифференцирования
Слайд 77Формулы численного дифференцирования с остаточными членами для узлов, расположенных с
постоянным шагом h
r=1, N=1 (два узла):
r=1, N=2 (три узла):
f '(x0 ) = (-3y0 + 4y1 - y2)/2h + h2f '''(x)/3
f '(x1 ) = (y2 - y0)/2h - h2f '''(x)/6 - центральная разность
f '(x2 ) = (y0 – 4y1 + 3y2)/2h + h2f '''(x)/3
Слайд 78r=2, N=2 (три узла):
В приведенных формулах ξ есть некоторая точка
(своя для каждой из формул) из интервала (x0 , xN).
Слайд 79Численное интегрирование
Задача численного интегрирования состоит в нахождении
приближенного значения интеграла:
В качестве
приближенного значения интеграла L[f]
рассмотрим следующее:
где li[f] - формула
для приближенного вычисления интеграла
на отрезке [xi-1,xi].
Слайд 80Формула прямоугольников.
Заменим на отрезке [xi-1, xi] функцию y=f(x) полиномом нулевой
степени
ξi = (xi+xi-1 ) /2
,
Для случая учета значений функции только
в конечных точках интервала
Слайд 81Формула трапеций
Проведем через точки: (xi-1, f(xi-1)), (xi, f(xi)) полином
первой степени
Слайд 82Лекция 6
Основы метода конечных разностей
Слайд 83Основная идея метода заключается в замене частных
производных их разностными
аппроксимациями.
Метод конечных разностей
Пусть у нас имеется некоторая функция двух
переменных
F(x,z). Пусть нам известны значения функции в некоторых
точках (х,z), (x+Δx,z), (x-Δx,z). Если ввести обозначения
F(x+Δx,z)=Fi+1, F(x,z)=Fi, F(x-Δx,z)=Fi-1, то можно записать
следующие аппроксимации частных производных
данной функции:
Слайд 84правая разностная схема,
левая разностная схема,
центральная разностная схема.
Слайд 85При необходимости можно получить аппроксимацию
производных более высоких порядков, например
для второй производной:
Слайд 86 1. В исследуемой области строится сетка путем
дискретизации области изменения
аргумента.
В результате получается конечное множество точек,
отстоящих друг от
друга на величину шага Δx.
Чаще всего используется постоянный шаг сетки Δx=const.
Искомая функция F аппроксимируется совокупностью
значений в узлах сетки Fi (сеточной функцией).
Метод конечных разностей предполагает выполнение
следующих шагов:
2. В исходных дифференциальных уравнениях
операторы ∂F/∂x, ∂2F/∂x2 заменяется конечной разностью
по одной из разностных схем. Записывается система
уравнений с конечными разностями для точек сетки.
Каждая точка сетки представляется шаблоном, отражающим
свойства среды и физического поля.
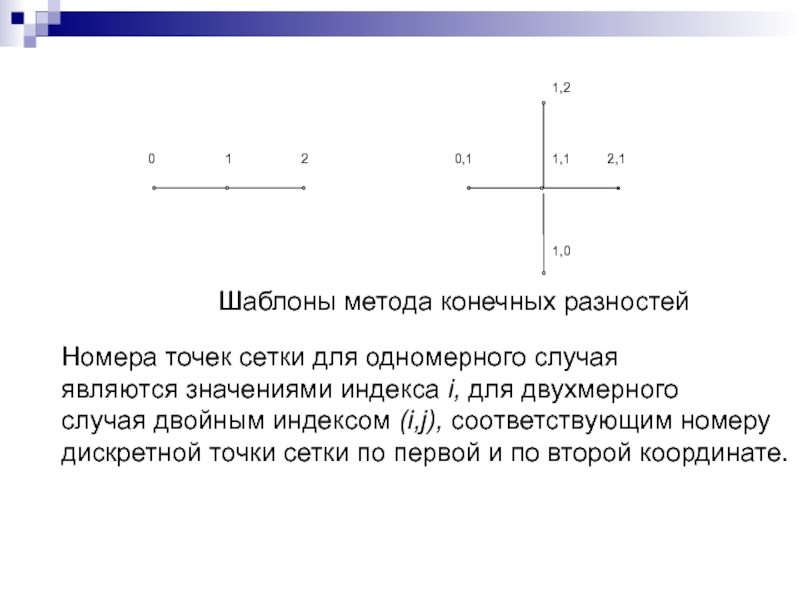
Слайд 87Шаблоны метода конечных разностей
Номера точек сетки для одномерного случая
являются значениями индекса i, для двухмерного
случая двойным индексом (i,j),
соответствующим номеру
дискретной точки сетки по первой и по второй координате.
Слайд 88Полученная система дополняется граничными и
начальными условиями. Для производных в
граничных условиях второго и третьего рода
также используется аппроксимация конечной
разностью.
В результате будет получена замкнутая система в общем
случае нелинейных алгебраических уравнений.
3. Полученная система алгебраических уравнений
решается численно.
Слайд 89Решение одномерных стационарных задач.
Используется два подхода при наличии краевых условий
Неймана (граничное условие выражается через производную):
1. не использовать дополнительных
виртуальных
узлов сетки и не использовать центральные
разности для граничного условия;
2. использовать дополнительный виртуальный
узел и центральную разность для граничного условия
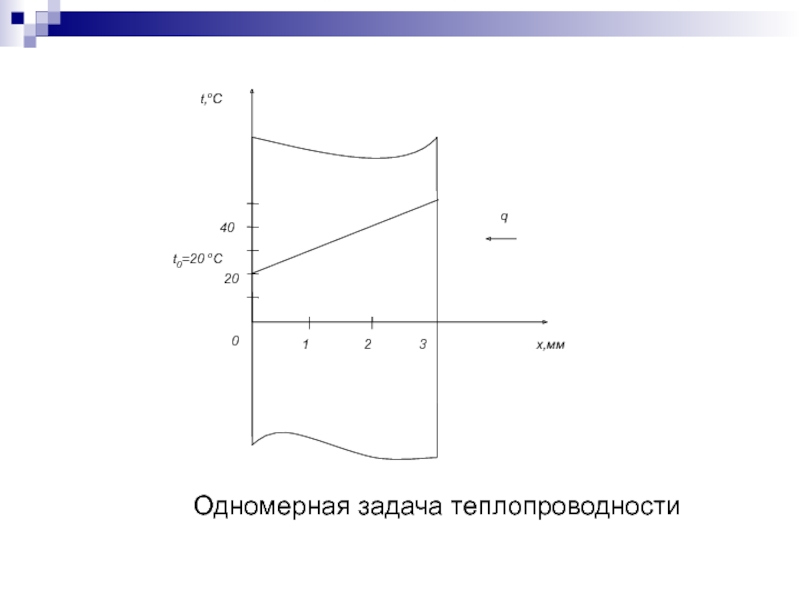
Слайд 90Рассмотрим стационарное распределение температуры
в плоской стенке толщиной 3 мм.
Такая модель
хорошо описывает процесс теплопроводности,
например, в стенке корпуса
ЭВС в точках, где
краевые эффекты оттока теплоты по краям стенки
незначительны и задачу можно считать одномерной.
Одна поверхность стенки находится при температуре
20оС, на другую поверхность падает тепловой поток
удельной мощностью q=104 Вт/м2 . Теплопроводность
стенки λ=1 Вт/(м⋅ оС).
Использование МКР рассмотрим на примере
Слайд 91Уравнение теплопроводности в этом случае будет иметь вид
Градиент температуры ∂t/∂x=q/λ=10
оС /мм.
Сделаем по координате x шаг сетки, равный 1
мм.
По толщине стенки получим четыре точки
Рассмотрим вариант решения задачи, при котором не
будем использовать дополнительных виртуальных узлов.
Слайд 92Одномерная задача теплопроводности
Слайд 93Система уравнений МКР в случае
отсутствия виртуальных узлов
t1=300C, t2=400C,
t3=500C.
Решение
Слайд 94
Система уравнений МКР в случае
наличия виртуального узла
Для граничных условий
первого рода на границе вместо
производной нужно было бы задать
температуру.
Слайд 95Решение одномерных нестационарных задач
Используют явный и неявный методы
В явном
методе последующие вычисления в следующих
точках сетки по времени базируются
на результатах
предыдущих вычислений. В неявном методе нужно
составить полную систему уравнений, которую затем
численно решить. Явные методы по сравнению с неявными
имеют большие ограничения по устойчивости
Рассмотрим варианты шаблонов для одномерной
нестационарной задачи теплопроводности. В этом
случае уравнение теплопроводности имеет вид:
Слайд 96При использовании правой и левой разностных схем для
аппроксимации производной
по времени применяется
четырехточечный шаблон.
Введем следующие обозначения:
Δτ
-
шаг по сетке времени;
- значение температуры в точке i в момент времени j.
Шаблон явного метода
Слайд 97Разностная аппроксимация дифференциального
уравнения теплопроводности для i –ой точки в
момент
времени j для явного метода
Значение температуры в следующий момент
времени
Слайд 98Пример. Имеем плоскую стенку толщиной 3 мм.
В момент времени
τ=0 одна поверхность стенки
остается при начальной температуре t=200С,
другая
начинает поддерживаться (термостатироваться)
при температуре 800С. Начальное распределение
температуры – равномерное с температурой t(x,0)=200С.
Коэффициент температуропроводности примем равным
10 -7 м2/c. Шаг сетки по координате x выберем равным
1мм, шаг сетки по времени выберем равным 1с.
Для данной задачи условие устойчивости вычислений
имеет вид:
Слайд 99Результаты расчета по явному методу
j
В рассмотренном примере Δx2/2a =
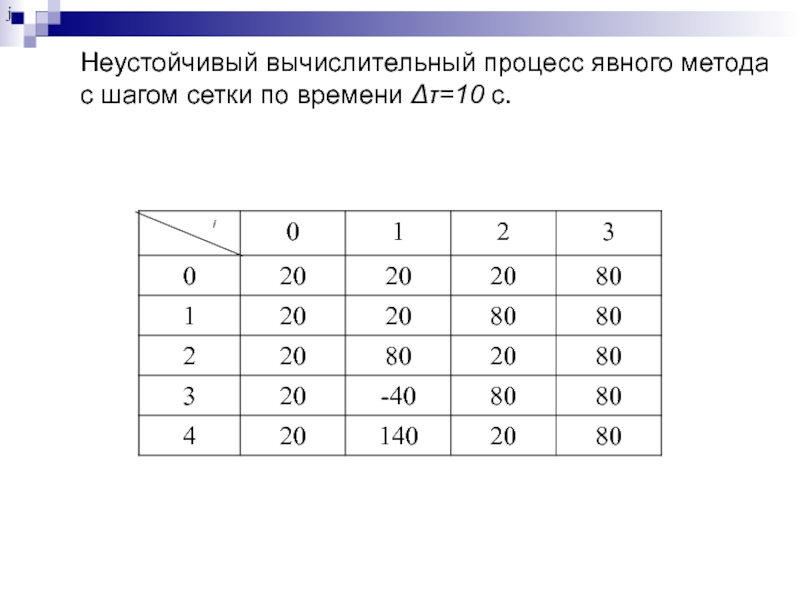
Слайд 100Неустойчивый вычислительный процесс явного метода
с шагом сетки по времени
Δτ=10 с.
j
Слайд 101Шаблон неявного метода
Разностная аппроксимация дифференциального уравнения
теплопроводности для i
–ой точки в момент времени j+1 для
неявного метода будет
иметь следующий вид:
При такой аппроксимации необходимо составить
систему уравнений для точек сетки, которую
потом нужно будет решать численными методами.
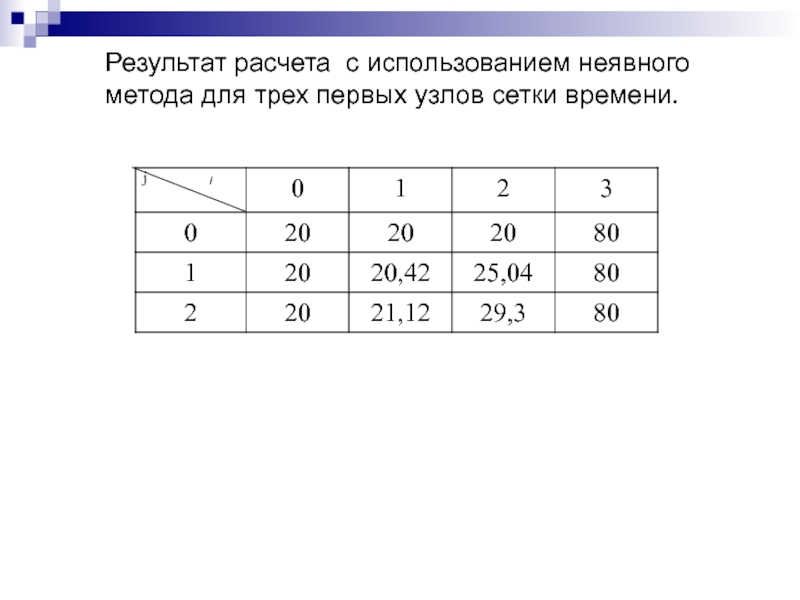
Слайд 102Результат расчета с использованием неявного
метода для трех первых узлов
сетки времени.
j
Слайд 103Лекция 7.
Решение двухмерных задач. Устойчивость, сходимость и погрешность конечно-разностных
аппроксимаций.
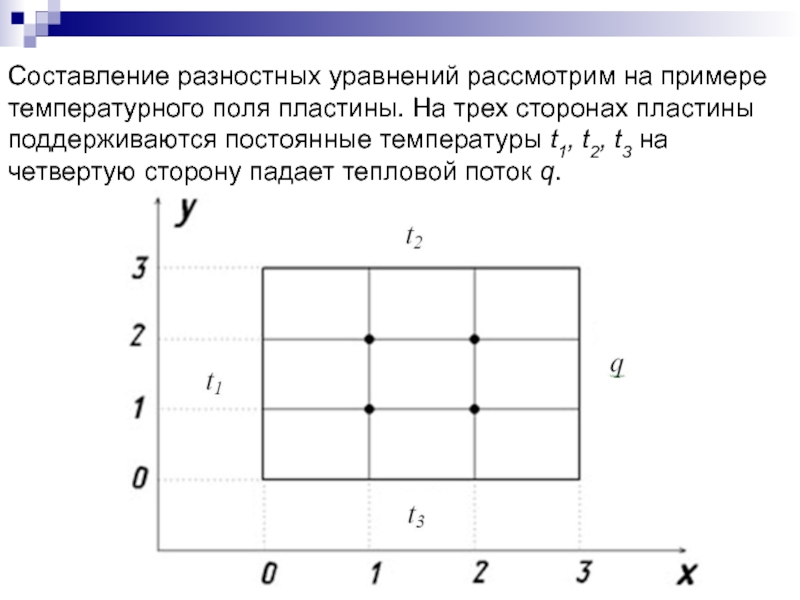
Слайд 104Составление разностных уравнений рассмотрим на примере
температурного поля пластины. На
трех сторонах пластины
поддерживаются постоянные температуры t1, t2, t3 на
четвертую сторону падает тепловой поток q.
Слайд 105Двухмерное стационарное уравнение теплопроводности:
В качестве шаблона будет использован двухмерный шаблон
0,1
1,1
2,1
1,0
1,2
Слайд 106Для внешних узлов на сторонах, где температура
поддерживается постоянной, нужно
записать равенства
температурам t1, t2 и t3. Для четвертой стороны:
Слайд 107Система уравнений для внутренних четырех узлов
(первый индекс по координате
x, второй – по координате y):
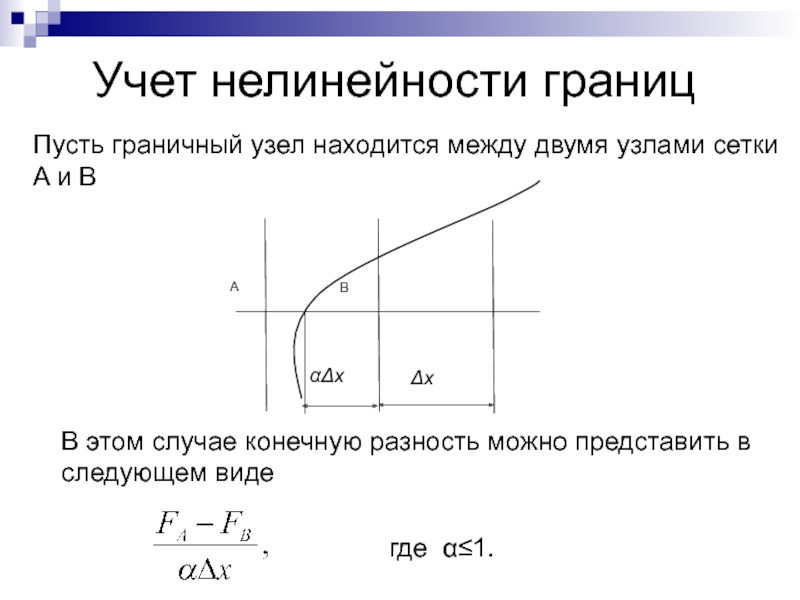
Слайд 108Учет нелинейности границ
Пусть граничный узел находится между двумя узлами сетки
A и B
В этом случае конечную разность можно представить
в
следующем виде
где α≤1.
Слайд 109
Погрешность аппроксимации первой производной
правой разностью
Погрешность аппроксимации первой производной
левой разностью
Погрешность аппроксимации второй производной
Слайд 110Основная идея метода конечных элементов.
Метод конечных элементов (МКЭ) основан на
аппроксимации
не производных, а самого решения F(X). Поскольку оно
заранее
не известно, то аппроксимация выполняется
выражением с неопределенными коэффициентами qi:
U(X)=Qϕ(X)
где Q=(q1, q2,……. qn) вектор неопределенных коэффициентов,
ϕ(X) –матрица опорных функций.
Слайд 111После подстановки U(X) в исходное дифференциальное
уравнение L F(X)=V(X), где
L- дифференциальный оператор,
получим систему невязок
L (Qϕ(X)) - V(X)= 0
Слайд 112Лекция 8
Топологические методы формирования математической модели на макроуровне.
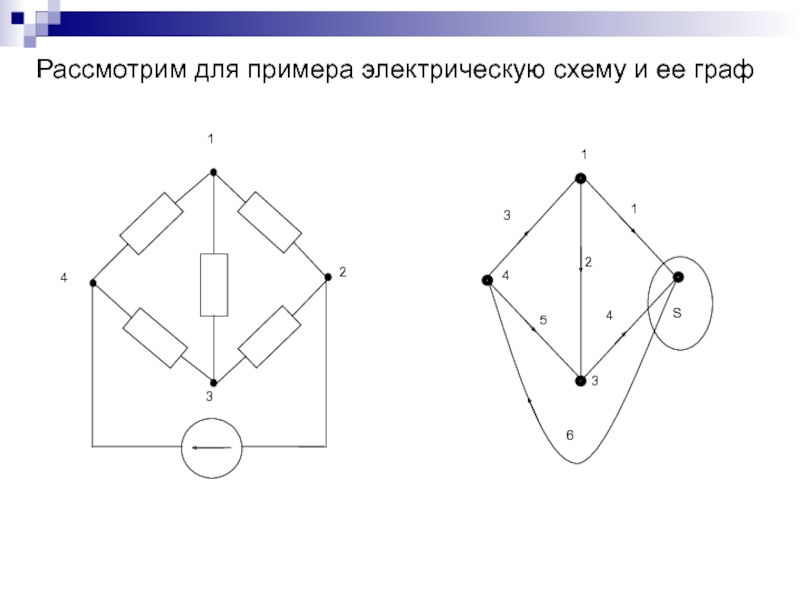
Слайд 113Рассмотрим для примера электрическую схему и ее граф
Слайд 114Топологические матрицы
Узловая матрица
Элемент этой матрицы aij (i –номер строки;
j –номер столбца)
равен 1, если ветвь j соединена с
узлом i и ориентирована от
него, -1, если ориентирована к нему, и 0, если ветвь j не
соединена с узлом i .
Слайд 115При расчетах один узел (любой) заземляют.
Целесообразно в качестве такого
узла использовать узел
с нулевым потенциалом. Тогда приходим к узловой
матрице
А (редуцированной матрице), которая может быть получена
из матрицы Aн путем вычеркивания строки, относящейся к
заземленному узлу. Например, при вычеркивании строки
“2” получим
Число строк матрицы А равно числу независимых
уравнений для первого закона Кирхгофа.
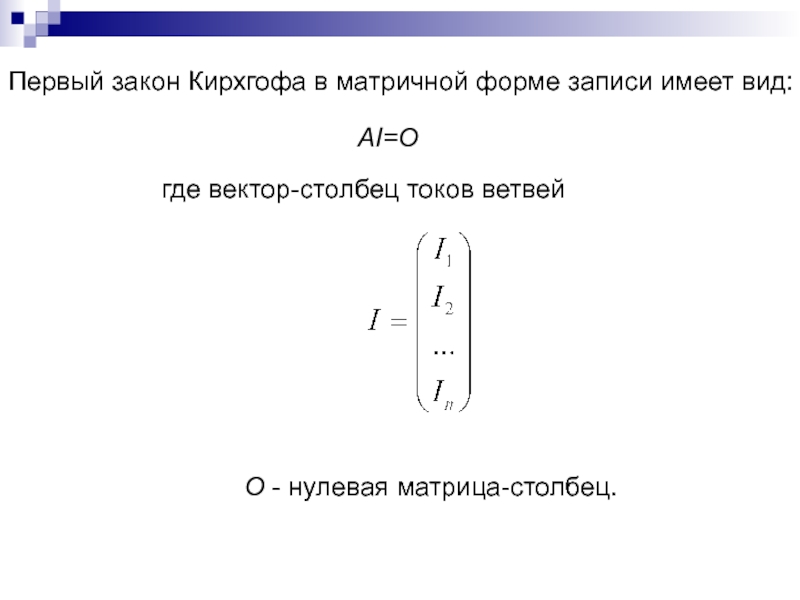
Слайд 116Первый закон Кирхгофа в матричной форме записи имеет вид:
АI=О
где вектор-столбец токов ветвей
O - нулевая матрица-столбец.
Слайд 117Контурная матрица
Элемент bij матрицы В равен 1, если ветвь
j входит в
контур i и ее ориентация совпадает с
направлением
обхода контура, -1, если не совпадает с направлением
обхода контура, и 0, если ветвь j не входит в контур i.
Матрицу В, записанную для главных контуров, называют
матрицей главных контуров. За направление обхода контура
принимают направление ветви связи этого контура.
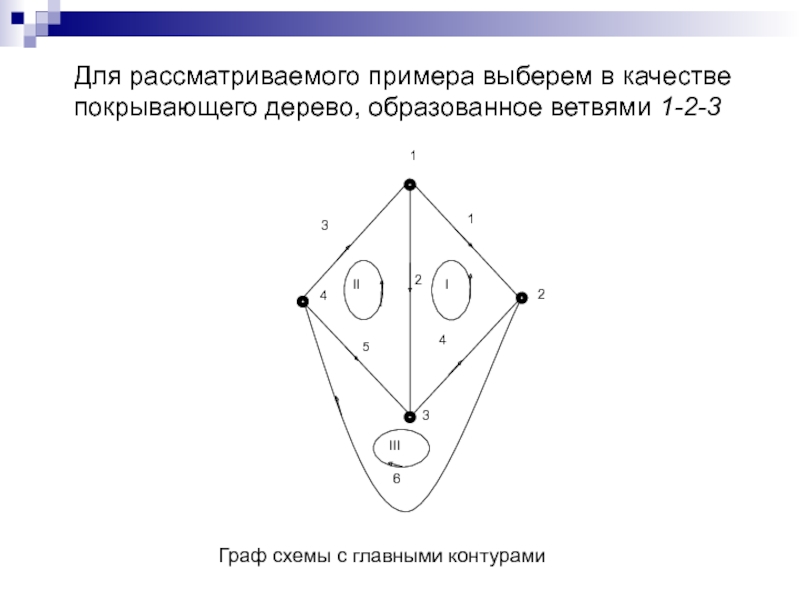
Слайд 118Для рассматриваемого примера выберем в качестве
покрывающего дерево, образованное ветвями
1-2-3
Граф схемы с главными контурами
Слайд 119Составим матрицу главных контуров В.
Введем вектор-столбец напряжений ветвей
Второй закон Кирхгофа
в матричной форме:
BU = O
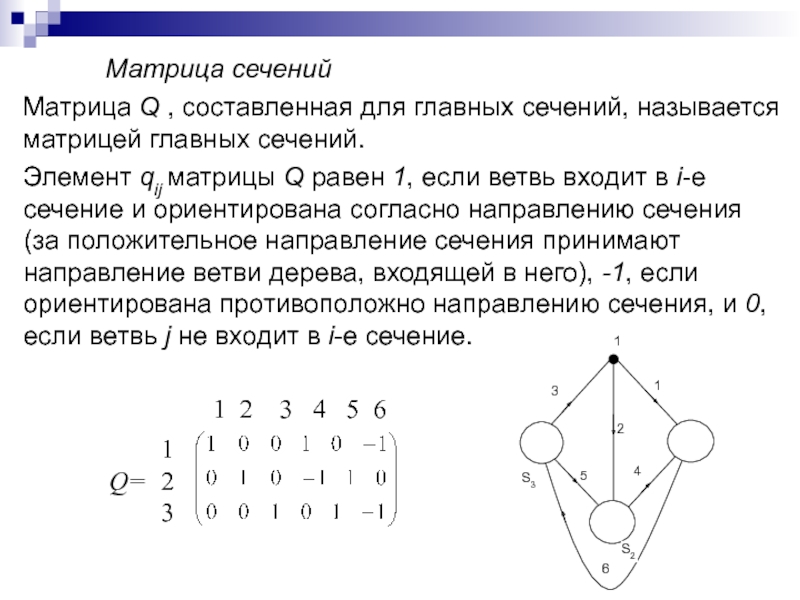
Слайд 120Матрица сечений
Матрица Q , составленная для главных сечений, называется
матрицей главных сечений.
Элемент qij матрицы Q равен 1, если
ветвь входит в i-е
сечение и ориентирована согласно направлению сечения
(за положительное направление сечения принимают
направление ветви дерева, входящей в него), -1, если
ориентирована противоположно направлению сечения, и 0,
если ветвь j не входит в i-е сечение.
Слайд 121Для топологических матриц А, В и Q, составленных
для одного
и того же графа, выполняются соотношения
АВТ= О;
QВТ= О,
где
О – нулевая матрица
Зная одну из топологических матриц, по ее структуре
можно восстановить остальные.
Слайд 122Анализ во временной области (динамический анализ).
Математическая модель во временной
области пассивного
фильтра нижних частот (изменение во времени напряжения
на
выходе фильтра).
RCdUa/dt + Ua = Ue
Слайд 123С математической точки зрения численное решение на
отрезке [a, b]
задачи Коши для дифференциального уравнения
первого порядка
y' = f(x, y),
y(a) = y0
состоит в построении таблицы приближенных значений
y0, y1, ..., yi, ... yN решения y(x) в узлах сетки. Если
xi = a+ i h, h=(b-a)/ N, то сетка называется равномерной.
При временном анализе в качестве переменной х
используется время.
Численный метод решения задачи Коши называется
одношаговым, если для вычисления решения в точке x0 + h
используется информация о решении только в точке x0.
Слайд 124 Метод Эйлера.
В методе Эйлера величины yi вычисляются по
формуле
yi+1 = yi + h f(xi , yi), i
= 0, 1, ...
Пример. Найдем методом Эйлера решение уравнения
при следующих начальных условиях: t=0, U=1.
Аналитическое решение этого уравнения с учетом заданных
начальных условий имеет вид:
Шаг сетки (шаг интегрирования) возьмем равным Δt=0,1.
Слайд 125t 0=0, U0= 1, t i+1 = t
i + 0.1, Ui+1 = Ui + 0.1(2t 2i
+ 2Ui).
Расчетные выражения
Слайд 126Метод Рунге-Кутта четвертого порядка
yi+1 = yi + h (k1
+ 2k2 + 2k3 + k4)/6 , i = 0,
1, ...
k1 = f(xi , yi),
k2 = f(xi+h/2, yi+hk1/2),
k3 = f(xi+h/2, yi+hk2/2),
k4 = f(xi+h, yi+hk3)
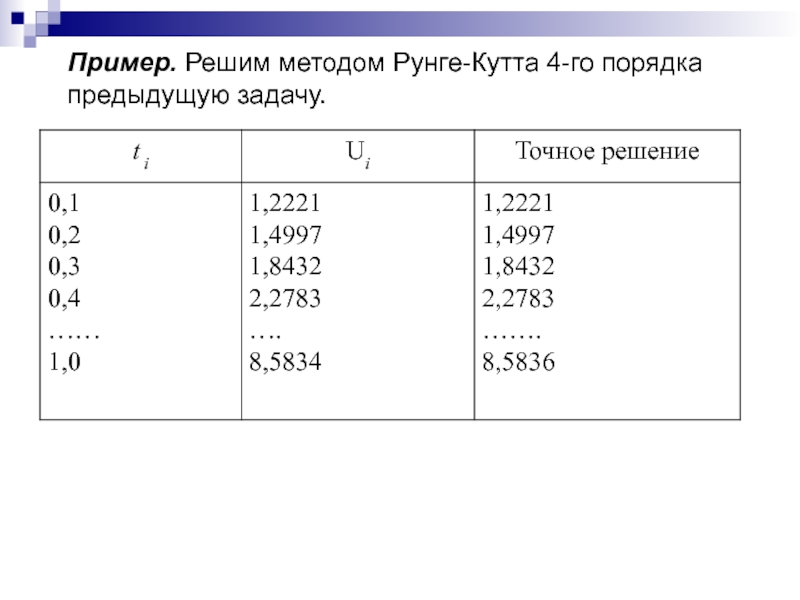
Слайд 127Пример. Решим методом Рунге-Кутта 4-го порядка
предыдущую задачу.
Слайд 128Для практической оценки погрешности проводят вычисления
с шагами h и
h/2. За оценку погрешности решения,
полученного с шагом h/2, принимают
величину, равную
где p - порядок метода, yi(h) - приближенное решение,
вычисленное с шагом h, y2i(h/2) - приближенное решение,
вычисленное с шагом h/2.
Для метода Рунге-Кутта 4 порядка точности оценка
погрешности может быть получена по выражению
max|y2i(h/2) - yi(h) |/15.
Слайд 129Анализ процессов в проектируемых объектах на
макроуровне в частотной области
Для линейных обыкновенных дифференциальных уравнений
справедливо применение преобразования Фурье для
сведения
дифференциальных уравнений к алгебраическим, в котором
оператор d/dt заменяется на частоты jω .
Пара взаимных преобразований Фурье (прямое и обратное)
имеет вид:
A(jω) - частотная характеристика анализируемой системы,
h(t) – импульсная характеристика (реакция системы на
единичный импульс – импульс единичной площади).
Слайд 130Для импульсных сигналов используется дискретное
преобразование (в том числе и
быстрое) Фурье прямое
и обратное.
,
k=0,N-1
, n=0,N-1
Слайд 131Лекция 9.
Анализ чувствительности, точности
и статистический анализ.
Слайд 132Абсолютный коэффициент чувствительности i-го выходного
параметра yi к j-му входному
параметру xj равен
при номинальных значениях входных параметров.
Относительный коэффициент
чувствительности определяется
по выражению
xjo и yi0 – номинальные значения параметров.
Слайд 133Пример. Мощность, рассеиваемая резистором может быть
рассчитана по формуле P=U2/R.
Номинальное значение
напряжения 1В, сопротивления резистора – 10 Ом.
Определить
относительные и абсолютные коэффициенты
чувствительности мощности к изменению приложенного
напряжения и сопротивления.
Au= 0,2 В/Ом; AR= -0,01 В2/Ом2
Bu=2; BR= -1
Слайд 134Анализ точности. Уравнение погрешности.
Выходной параметр изделия или технологического процесса
представляет
собой функцию от параметров
входящих в это устройство элементов:
Возьмем полный
дифференциал и, перейдя к конечным
приращениям, получим
- уравнение для абсолютной погрешности
Уравнение для относительной погрешности
Слайд 135Метод наихудшего случая оценки точности
Рассмотрим суть метода на примере абсолютных
отклонений.
При определении коэффициентов чувствительности часть
из них будет положительна,
а часть - отрицательна.
Пусть Ai>0 ∀
Ai<0 ∀
;
Наихудшие отклонения выходных параметров
Слайд 136Пример. Для примера с определением коэффициентов
чувствительности оценим предельную относительную
погрешность мощности при погрешности измерения
напряжения +4% -2% и погрешности
сопротивления ±10%.
Уравнение относительной погрешности
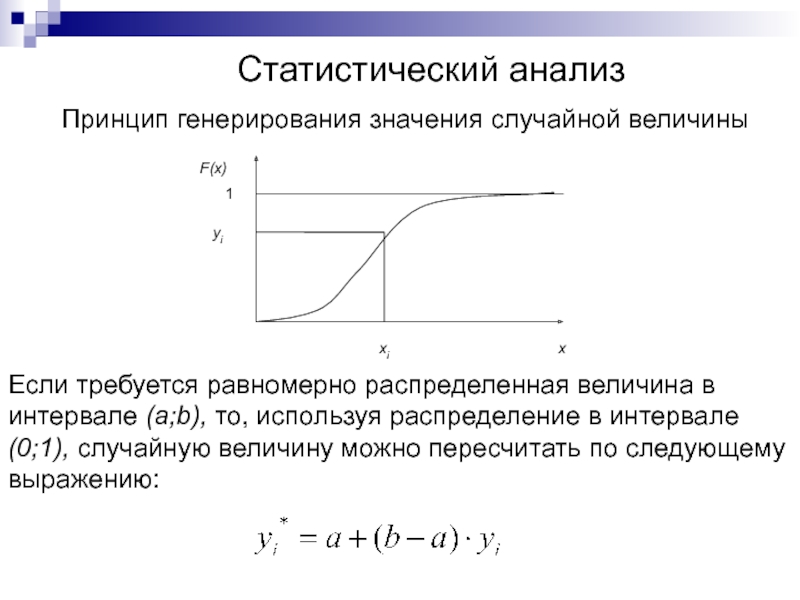
Слайд 137Статистический анализ
Принцип генерирования значения случайной величины
Если требуется равномерно
распределенная величина в
интервале (a;b), то, используя распределение в интервале
(0;1), случайную величину можно пересчитать по следующему
выражению:
Слайд 138Для экспоненциального закона распределения
где yi – значения равномерно распределенной
случайной
величины в интервале от 0 до 1.
Для нормального закона
распределения
где M(x) – математическое ожидание распределения
независимой случайной величины x; σx - среднеквадратичное
отклонение случайной величины x, m – параметр, задающий
точность вычисления (практически принимает значения от 5
до 15), yi – значения равномерно распределенной случайной
величины в интервале от 0 до 1.
Слайд 139Лекция 10.
Модели сигналов и
элементов цифровых устройств.
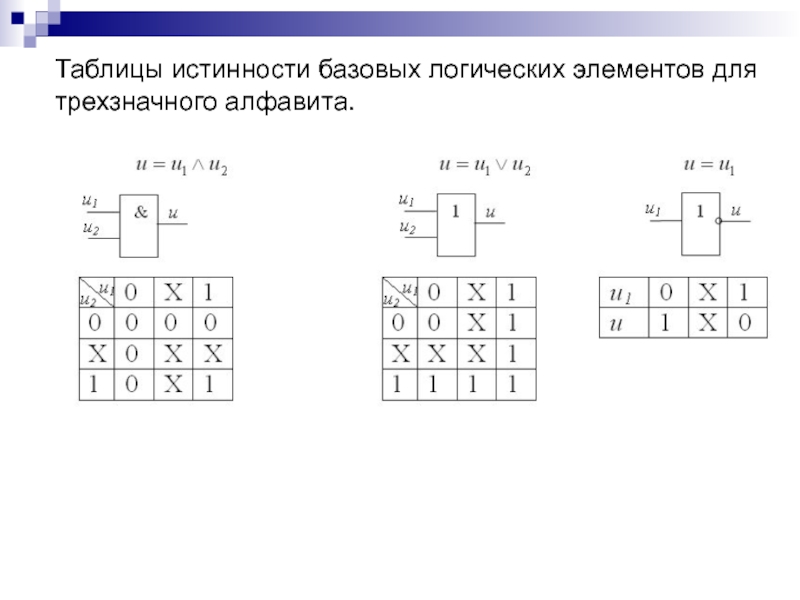
Слайд 140Таблицы истинности базовых логических элементов для
трехзначного алфавита.
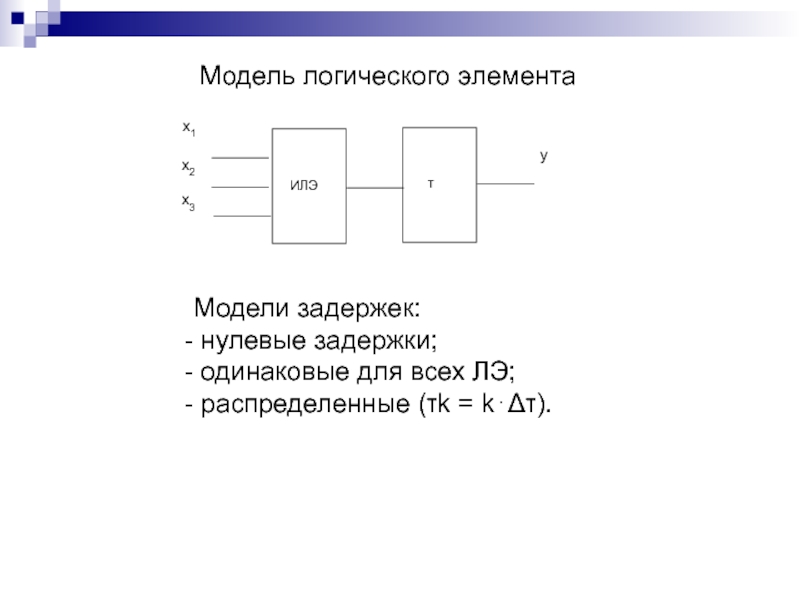
Слайд 141Модель логического элемента
Модели задержек:
нулевые задержки;
одинаковые для всех ЛЭ;
распределенные (τk = k⋅Δτ).
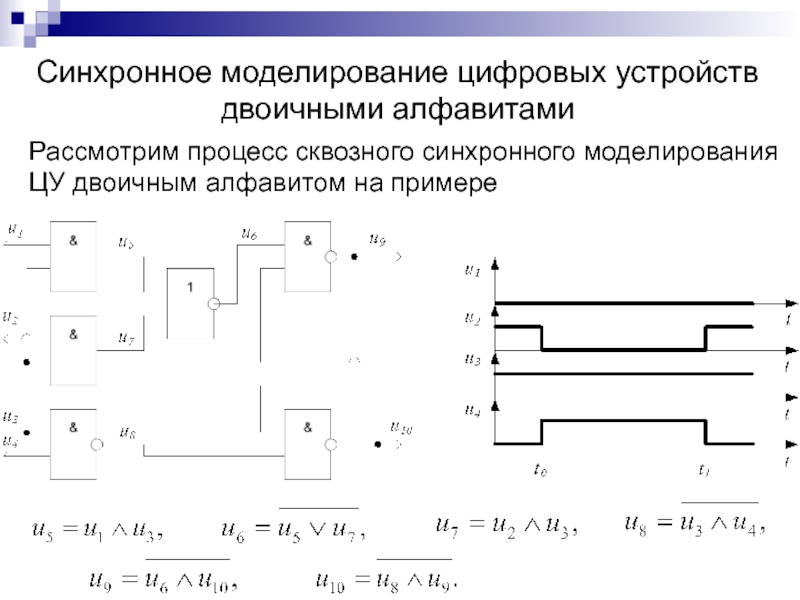
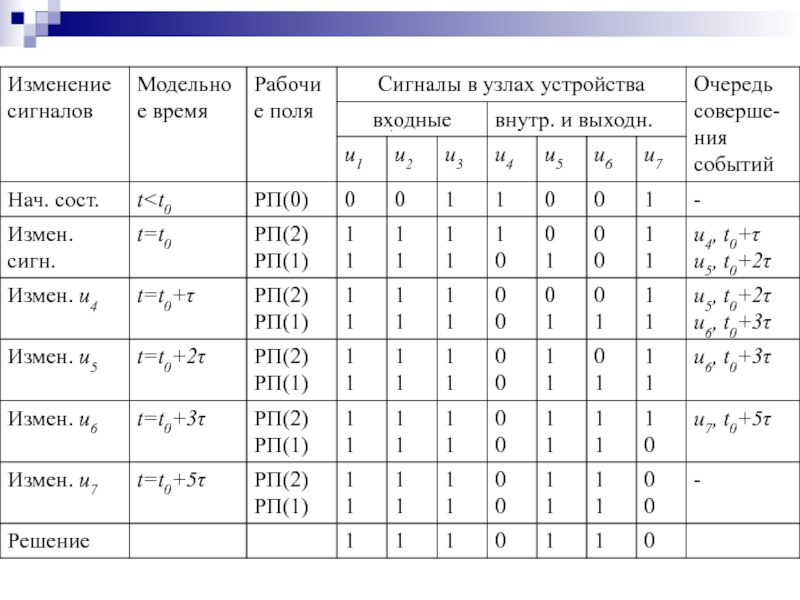
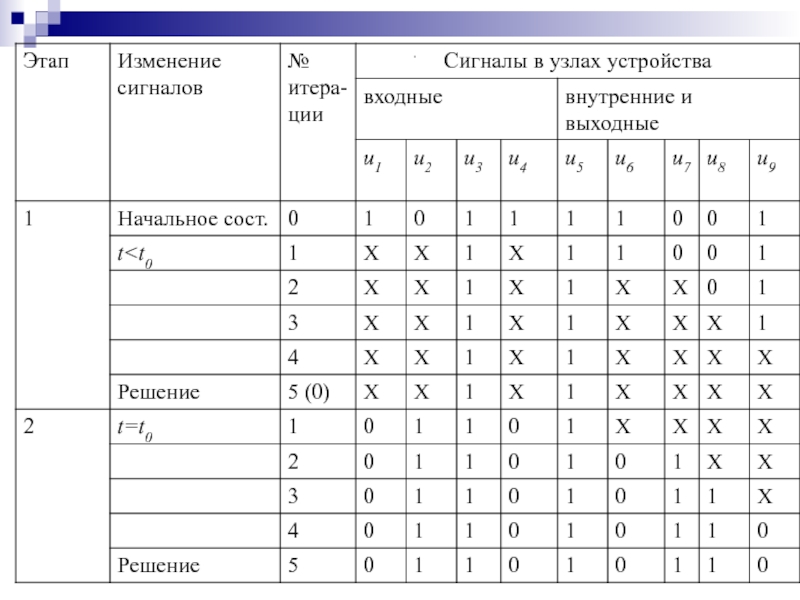
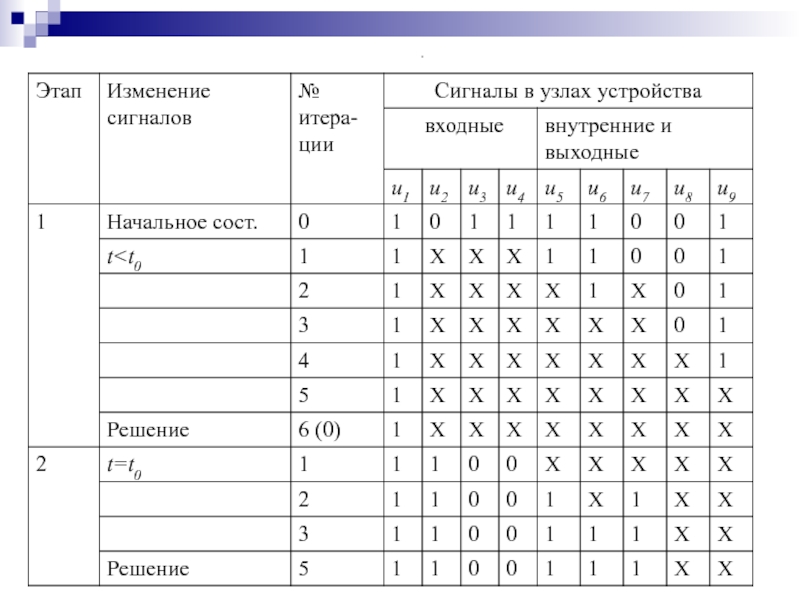
Слайд 142Синхронное моделирование цифровых устройств
двоичными алфавитами
Рассмотрим процесс сквозного синхронного моделирования
ЦУ двоичным алфавитом на примере
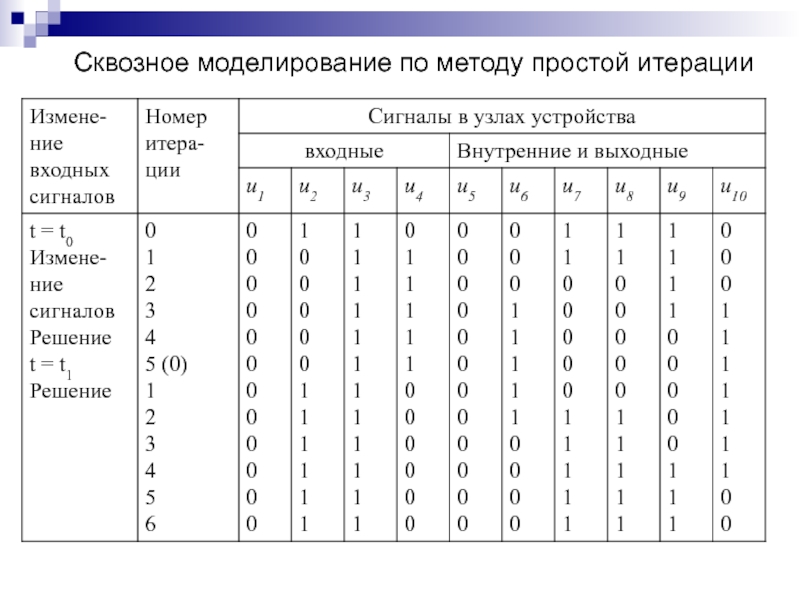
Слайд 143Сквозное моделирование по методу простой итерации
Слайд 145Лекция 11.
Асинхронное двоичное моделирование
цифровых устройств.
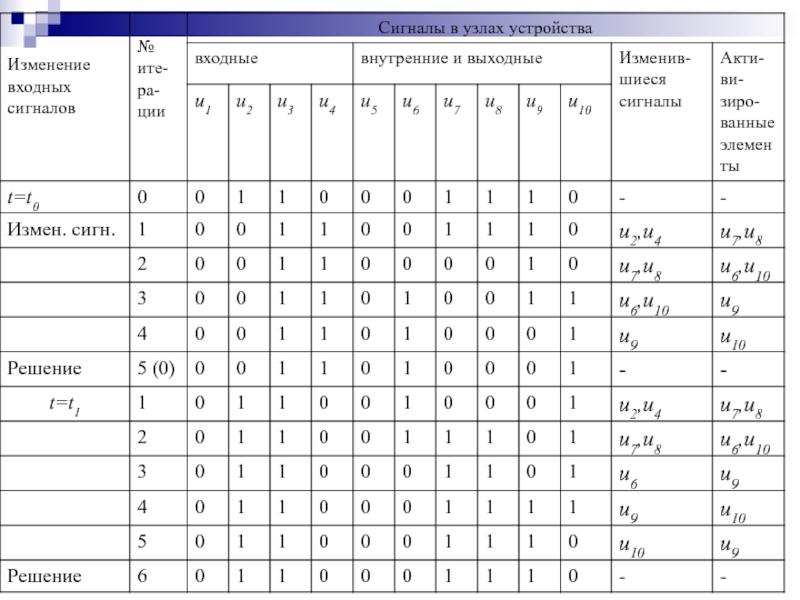
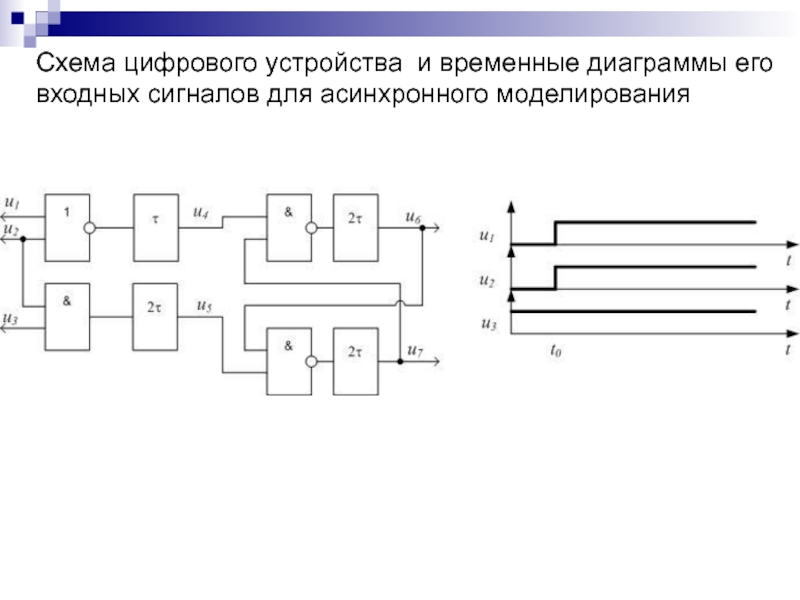
Слайд 146Схема цифрового устройства и временные диаграммы его
входных сигналов для
асинхронного моделирования
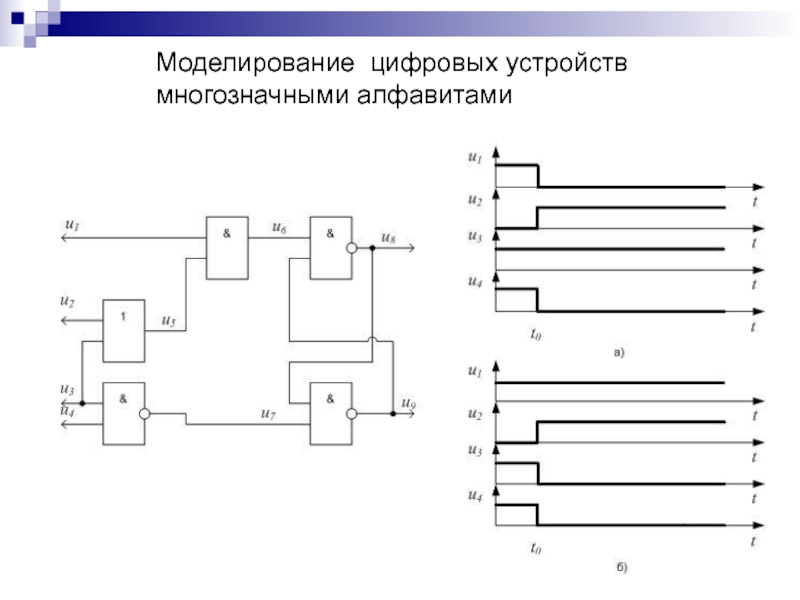
Слайд 148Моделирование цифровых устройств
многозначными алфавитами
Слайд 151Лекция 12
Марковские случайные процессы. Потоки событий. Основные понятия теории СМО.
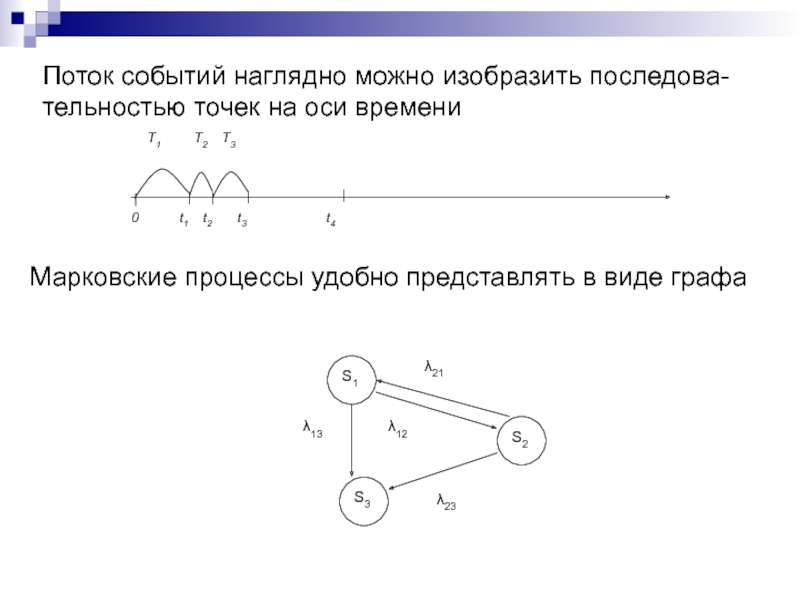
Слайд 152Поток событий наглядно можно изобразить последова-
тельностью точек на оси времени
Марковские процессы удобно представлять в виде графа
Слайд 153Вероятность перехода из состояния Si в состояние Sj за
время
Δt связана с интенсивностью потока событий λij,
переводящего систему из
состояния Si в состояние Sj
следующим выражением
Для простейшего потока интервал времени между соседними
событиями подчиняется экспоненциальному закону
распределения.
Слайд 154Показатели эффективности СМО
Вероятность обслуживания - это вероятность того, что
произвольно
выбранная из входящего потока с
интенсивностью λ заявка будет обслужена,
т.е. окажется в
потоке обслуженных заявок с интенсивностью λоб
Pоб=λоб /λ
λ=λоб+λотк , где λотк - интенсивность потока заявок,
получивших отказ.
Вероятность отказа
Pот=1 - Pоб
Pот= Pпр+ Pоб+ Pож ,
где Pпр - вероятность отказа при приходе; Pоб - вероятность
отказа при обслуживании; Pож - вероятность отказа при
ожидании.
Слайд 155Среднее время ожидания
где F(tобсл)- функция распределения времени обслуживания.
где F(tож)-
функция распределения времени ожидания.
Среднее время обслуживания
Среднее время пребывания требования в
СМО
Слайд 156Средняя длина очереди
представляет собой математическое ожидание числа заявок,
находящихся
в очереди. Для ее определения в общем
случае необходимо знание
совокупности вероятностей Pожi
(вероятности нахождения в очереди i заявок)
где n – число мест в очереди.
Среднее число занятых каналов обслуживания
Pзанi вероятность того, что в произвольный момент времени
занято обслуживанием i каналов.
где m – число каналов в системе,
Слайд 157Среднее число заявок в системе - математическое ожидание
числа заявок,
находящихся в очереди или в каналах
обслуживания
Слайд 158Аналитические модели СМО
Основой построения аналитических моделей СМО являются
уравнения Колмогорова
Изменение вероятности Pi нахождения системы в
состоянии
Si за время Δt есть вероятность перехода
системы в состояние Si, из любых других состояний за
вычетом вероятности перехода из состояния Si, в другие
состояния за время Δt
где Pi(t) и Pj(t) — вероятности нахождения системы в
состояниях Si и Sj соответственно в момент времени t, a
Pji(Δt) и Pik(Δt) — вероятности перехода из состояний в
течение времени Δt ; J и К— множества индексов
инцидентных вершин по отношению к вершине Si по
входящим и исходящим дугам на графе состояний
соответственно.
Слайд 159Разделив на Δt и перейдя к пределу при Δt →0,
noлучим
Откуда
В стационарном состоянии при t→∞ dPi/dt = 0
Слайд 160Лекция 13.
Примеры аналитической
модели СМО.
Имитационное моделирование СМО.
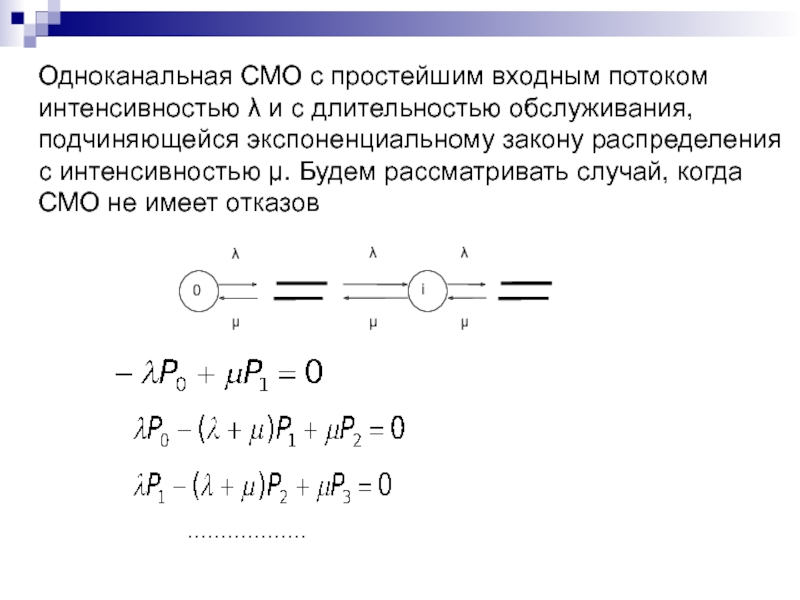
Слайд 161Одноканальная СМО с простейшим входным потоком
интенсивностью λ и с
длительностью обслуживания,
подчиняющейся экспоненциальному закону распределения
с интенсивностью μ. Будем
рассматривать случай, когда
СМО не имеет отказов
………………
Слайд 162
где α=λ/μ - приведенная интенсивность потока заявок
Установившийся режим возможен только
при α < 1
Слайд 163С учетом того, что
вероятность нахождения системы в состоянии S0
Показатели
эффективности СМО:
Слайд 164Средние времена пребывания в системе и очереди находят
с помощью
соотношений
,
которые называют формулами Литтла, где
Слайд 165Пример резервированной вычислительной системы
Слайд 166В результате решения этой системы можно определить
искомые выражения для
коэффициентов готовности и простоя
Слайд 167Пример двухпроцессорной системы
Вероятность отказа при приходе Pопп=P6
Вероятность отказа
при обслуживании
Вероятность отказа при ожидании
Pот=Pопп+ Pопо+ Pопож
Pоб=
1 - Pот
Слайд 168Лекция 14.
Виды моделей данных в сапр. Реляционные модели данных.
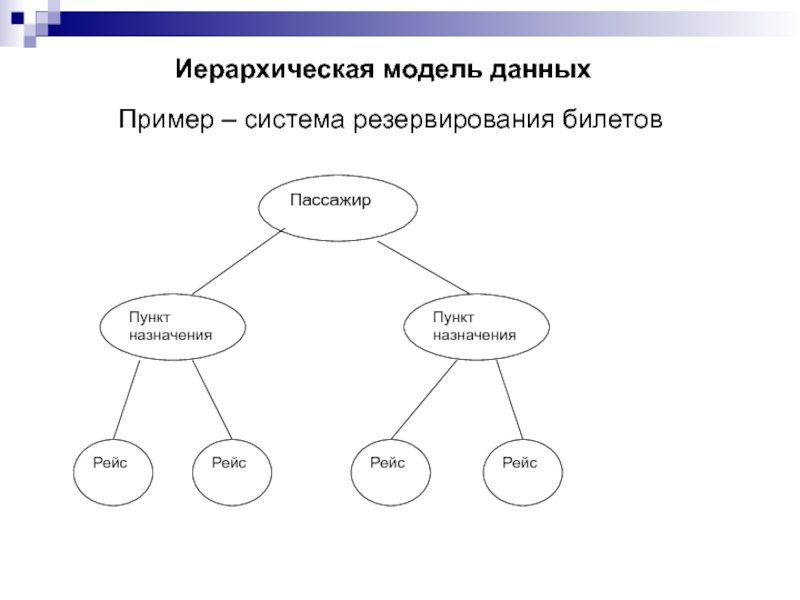
Слайд 169Иерархическая модель данных
Пример – система резервирования билетов
Слайд 170К основным недостаткам иерархических моделей данных
следует отнести:
неэффективность реализации отношений типа многие ко
многим,
медленный доступ
к сегментам данных нижних уровней
иерархии,
четкая ориентация на определенные типы запросов.
В сетевой модели для сегментов данных допускается
несколько входных сегментов наряду с возможностью
наличия сегментов без входов с точки зрения иерархической
структуры.
Графическое изображение структуры связей сегментов
такого типа моделей представляет собой сеть.
Слайд 171Реляционная модель ориентирована на организацию
данных в виде
двумерных таблиц.
Операции в реляционной модели
В реляционных БД основными
операциями над таблицами
являются:
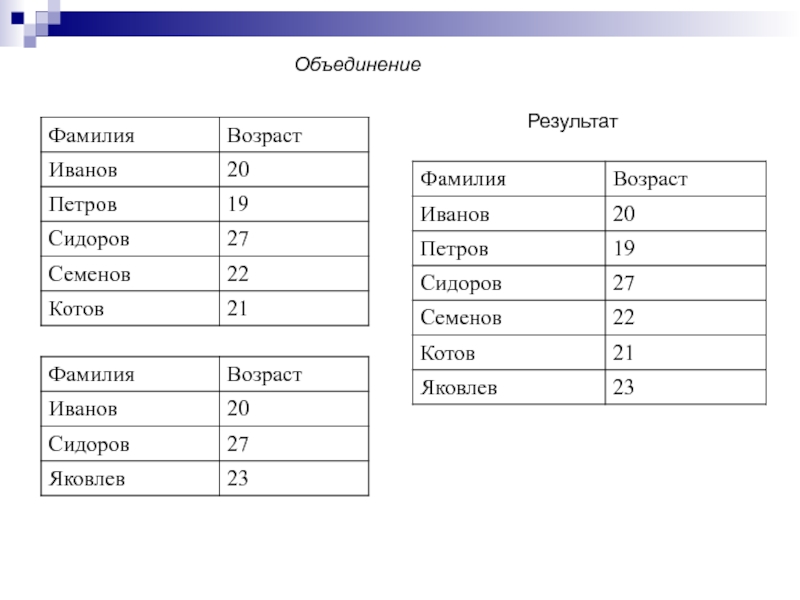
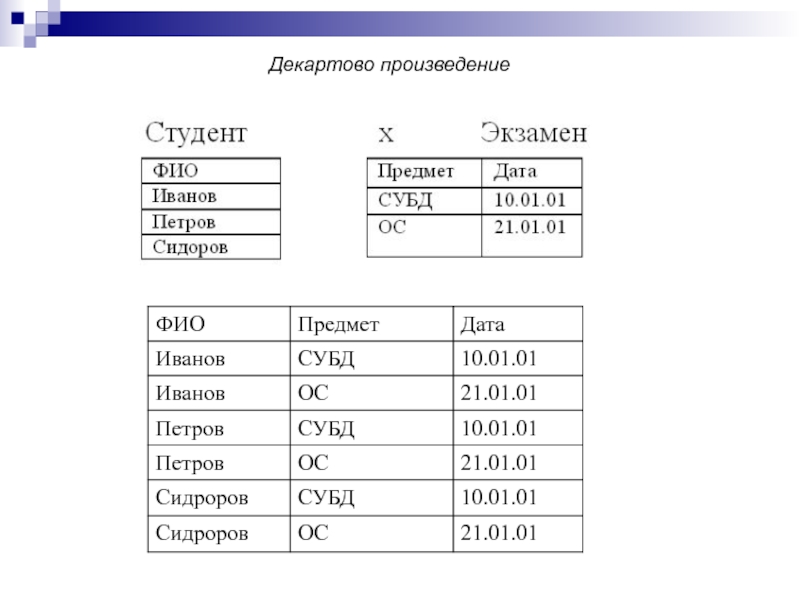
обычные традиционные операции над множествами
(объединение, пересечение, разность, декартово
пересечение, деление)
специальные реляционные операции
(проекции, соединения, выбора)
Слайд 175Проекция
Проекция выполнена на атрибуты Возраст и Группа.
Слайд 176Соединение.
В качестве атрибута для соединения выбран код студента
Слайд 177Типы связей (отношений) между таблицами
“один – к одному”
”один–ко-многим”
“многие-к-одному”
“многие-ко-многим”
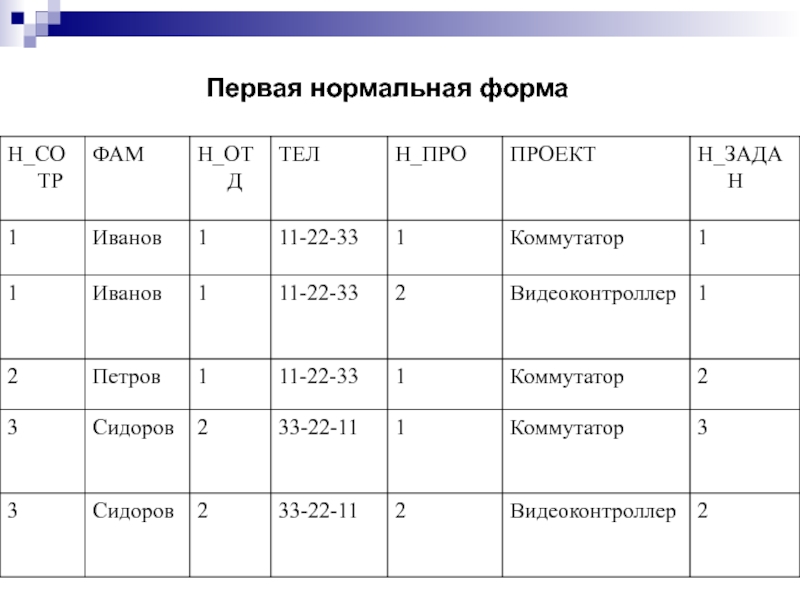
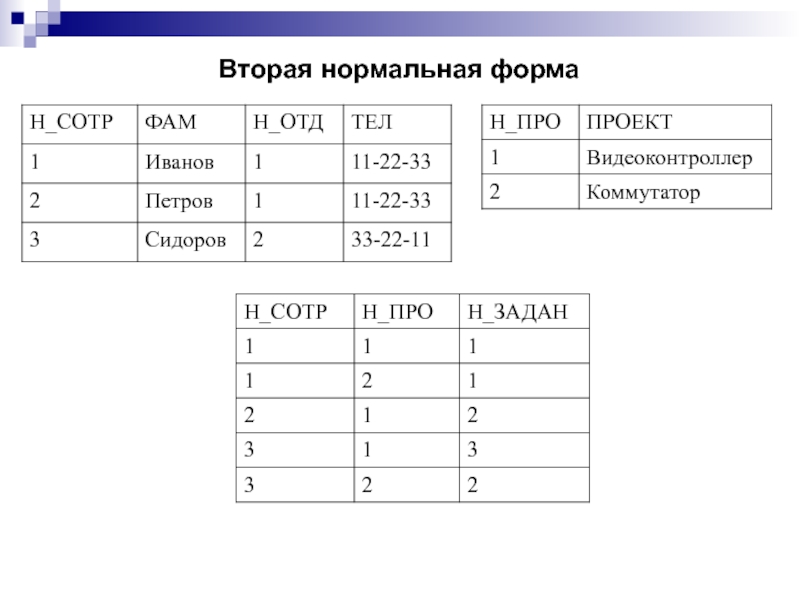
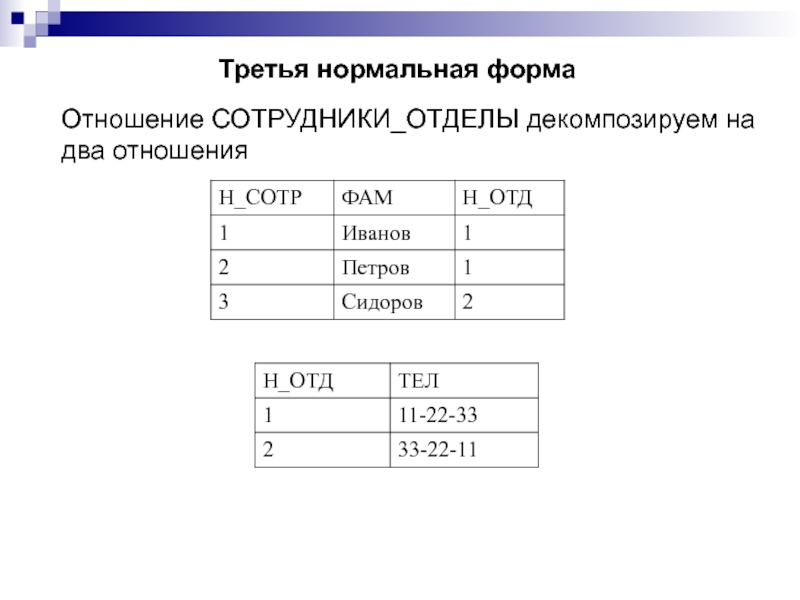
Слайд 180Третья нормальная форма
Отношение СОТРУДНИКИ_ОТДЕЛЫ декомпозируем на
два отношения
Слайд 181Оптимальное проектирование ЭВС
Лекция 15. Постановка задачи и классификация методов
оптимального проектирования.
Слайд 182Пусть каждый известный вариант решения задачи
оптимизации характеризуется многомерным вектором
X=(x1,x2,x3…..xn)
В каждой конкретной технической задаче оптимизации
множество векторов X,
на котором определена целевая
функция F(X), всегда ограничено некоторой допустимой
областью G.
gj(X)=0, j=1,2…m
gi(X) {≤ , ≥} 0, i=1,2…k
Кратко задачу оптимизации можно записать в следующем виде
Слайд 183Пример. Необходимо разработать корпус ЭВС в форме
параллелепипеда с объемом
не менее 1000 см3 и
минимальной площадью поверхности стенок. Толщину
стенок рассматривать не будем. Обозначим через xi
размеры параллелепипеда.
Слайд 184Многокритериальные задачи оптимизации.
Метод главного критерия.
min F1(X), при ограничениях
F2(X)≤ F2д(X), F3(X)≤ F3д(X),
…… Fn(X)≤ Fnд(X), где
Fiд(X) -
максимально допустимое значение i-го
частного критерия.
Метод взвешивания критериев оптимизации.
αi – весовой коэффициент.
Слайд 185Постановка задачи линейного программирования
max(min)
Каноническая форма (канонический вид) записи ЗЛП
Слайд 186Задача о назначениях. Пусть имеется n мест на плате для
размещения n элементов, причем на каждом месте может быть
размещена
только одна микросхема. Эффективность размещения
i-й микросхемы на j-м месте (например суммарная длина
связей).
На основании этих данных можно построить квадратную
матрицу
Требуется так распределить n микросхем на n мест на плате,
чтобы сумма эффективностей их размещения была
максимальной (для длины связей – была минимальной).
Определим некоторую матрицу
, в которой
Слайд 187Математическая модель задачи оптимизации
max
Слайд 188В общем случае задача оптимизации решается в K-мерном
пространстве. При
этом мерность пространства зависит как
от числа переменных n, так
и от вида ограничений. В случае,
если все m ограничений имеют вид неравенств, то K=n.
Если все m ограничений имеют вид уравнений, то K=n-m.
В случае, если m ограничений - в виде уравнений, а l - в
виде неравенств, то K=n+l-m.
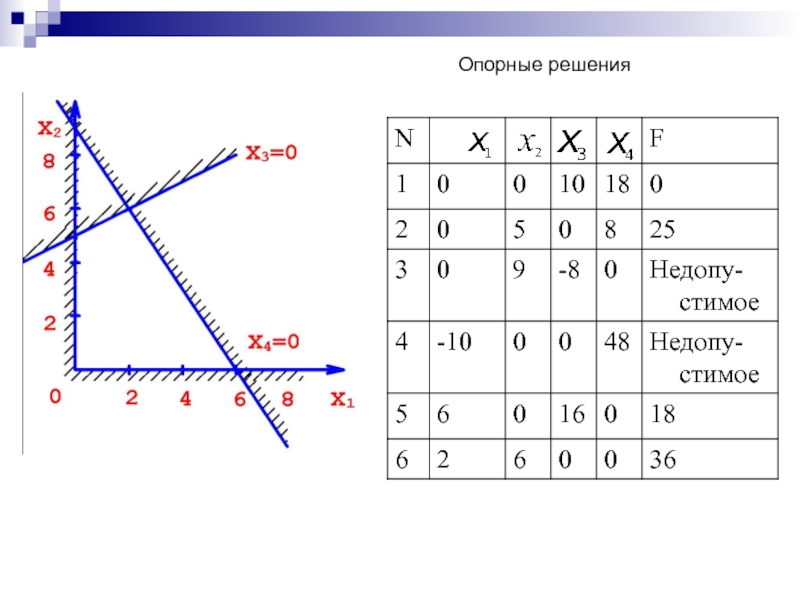
Слайд 193Пример записи ЗЛП в допустимом каноническом виде:
;
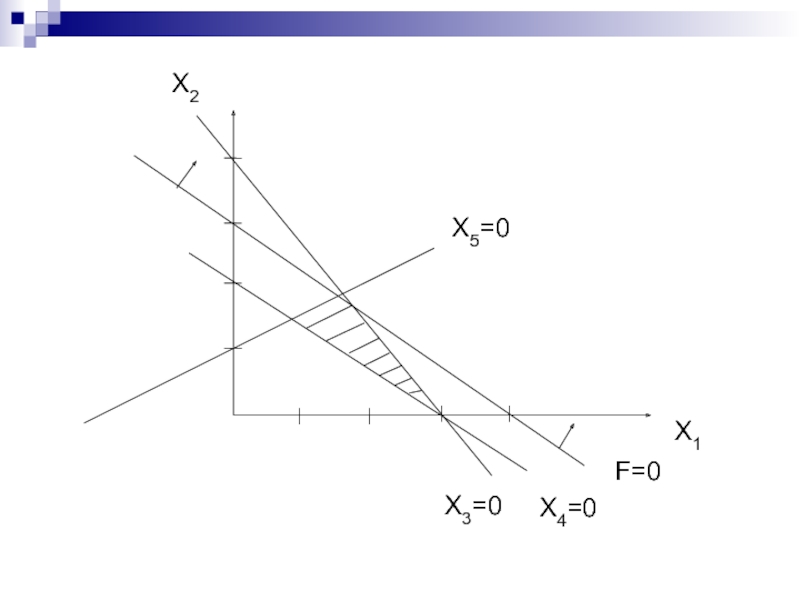
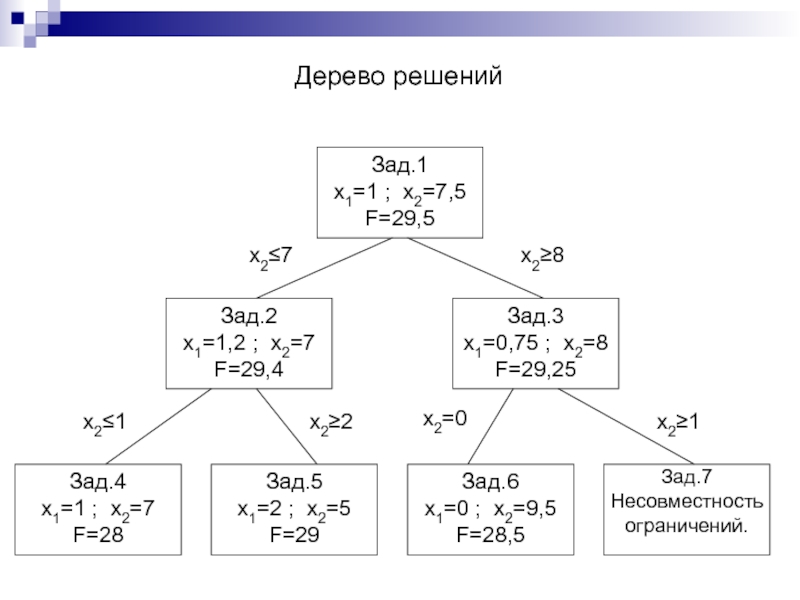
Слайд 194Найдем все опорные решения для следующей ЗЛП:
Слайд 197Лекция 17. Алгоритм
симплекс-метода.
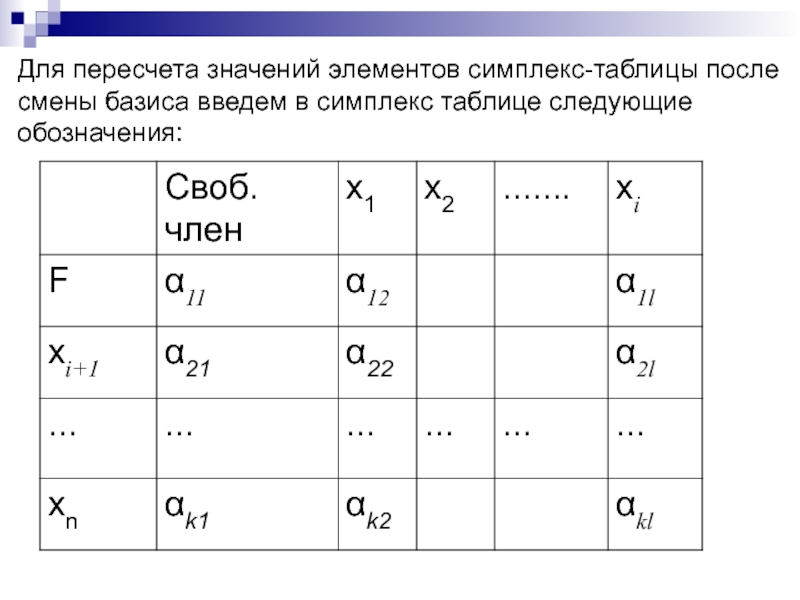
Слайд 198Для пересчета значений элементов симплекс-таблицы после
смены базиса введем в
симплекс таблице следующие
обозначения:
Слайд 199С учетом того, что αrp - разрешающий элемент (r, q
- строка,
p, s - столбец)
p, (разрешающая строка)
при
q=r; s=p, (для разрешающего элемента)
при q
r; s=p; (разрешающий столбец)
при q=r; s
для остальных элементов
Слайд 200Запишем ранее рассмотренную задачу в стандартной форме:
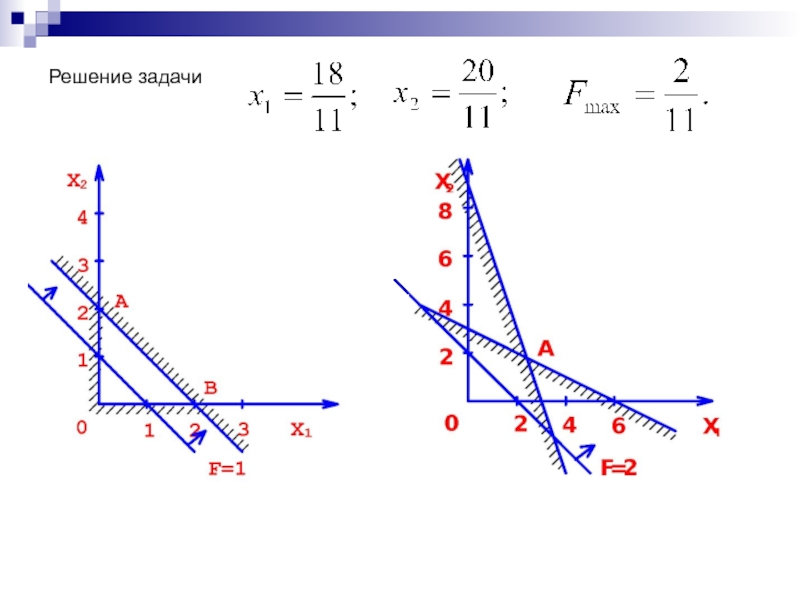
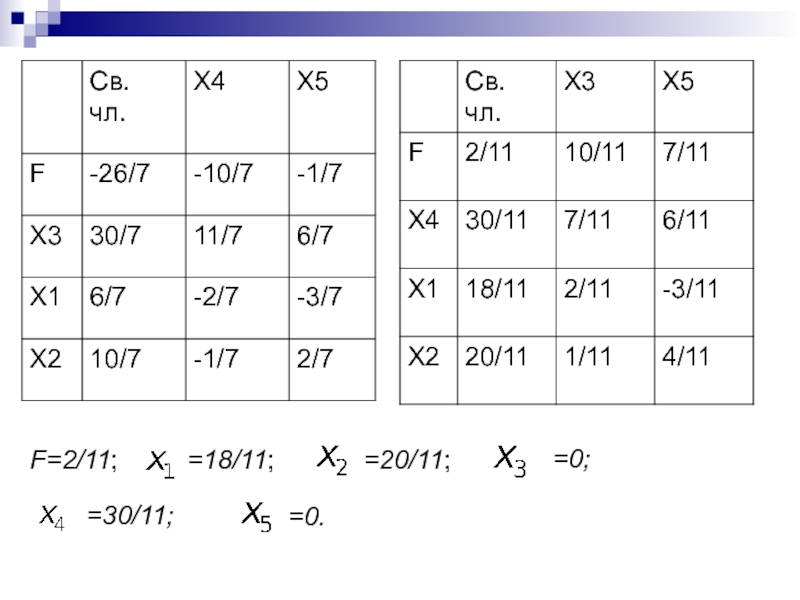
Слайд 201F=2/11;
=18/11;
=20/11;
=0;
=30/11;
=0.
Слайд 202Лекция 18
Постановка задачи целочисленного программирования
Слайд 203Постановка задачи целочисленного программирования.
max(min)
,
;
, (
), xj – целые числа.
Слайд 204Метод ветвей и границ
На основании полученного решения составляются
дополнительные к
исходной задаче ограничения
и
где [xj] - целая часть нецелочисленного значения
переменной в оптимальном решении.
Пример. Найти максимум F=7x1 + 3x2 → max
5x1 + 2x2≤ 20
8x1 + 4x2≤ 38; xj ≥ 0, целочисленные
Слайд 206Лекция 19. Нелинейное программирование.
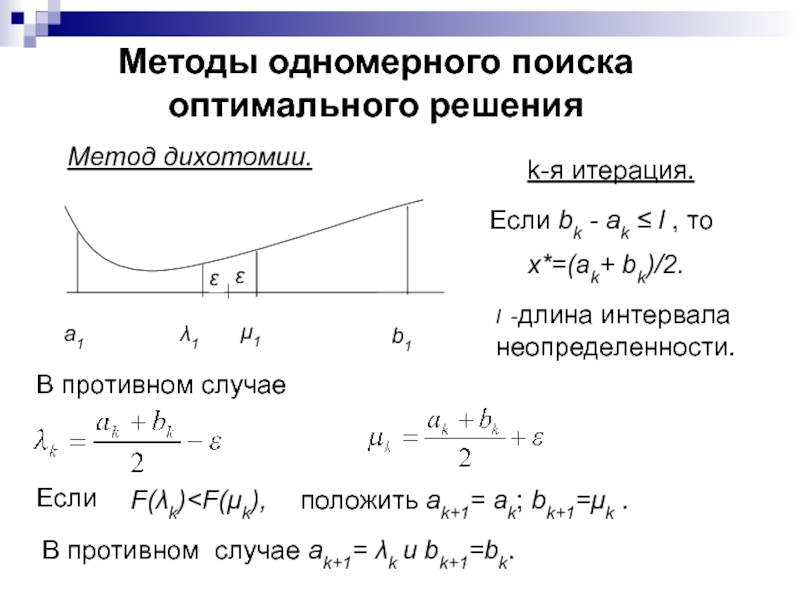
Слайд 207Методы одномерного поиска
оптимального решения
Метод дихотомии.
k-я итерация.
Если bk
- ak ≤ l , то
l -длина интервала
неопределенности.
x*=(ak+ bk)/2.
В противном случае
Если
F(λk)положить ak+1= ak; bk+1=μk .
В противном случае ak+1= λk и bk+1=bk.
Слайд 208Метод золотого сечения.
Предварительный этап. Выбрать допустимую конечную
длину интервала
неопределенности l>0.
Пусть [a1,b1] - начальный интервал неопределенности. Положить
λ1=a1+(1-α)(
b1 - a1) и μ1=a1+α( b1 - a1), где α=0,618. Вычислить
F(λ1) и F(μ1), положить k=1, и перейти к основному этапу.
Основной этап. Шаг 1. Если bk - ak ≤ l , то вычисления
заканчиваются x*=(ak+ bk)/2. В противном случае, если
F(λk)>F(μk), то перейти к шагу 2, если F(λk)≤F(μk), перейти
к шагу 3.
Шаг 2. Положить ak+1= λk, bk+1=bk, λk+1=μk,
μk+1= ak+1+α( bk+1 – ak+1). Вычислить F(μk+1), перейти к шагу 4.
Шаг 3. Положить ak+1= ak, bk+1=μk , μk+1=λk ,
λk+1= ak+1+(1-α)( bk+1 – ak+1). Вычислить F(λk+1).
Шаг 4. Присвоить k=k+1, перейти к шагу 1.
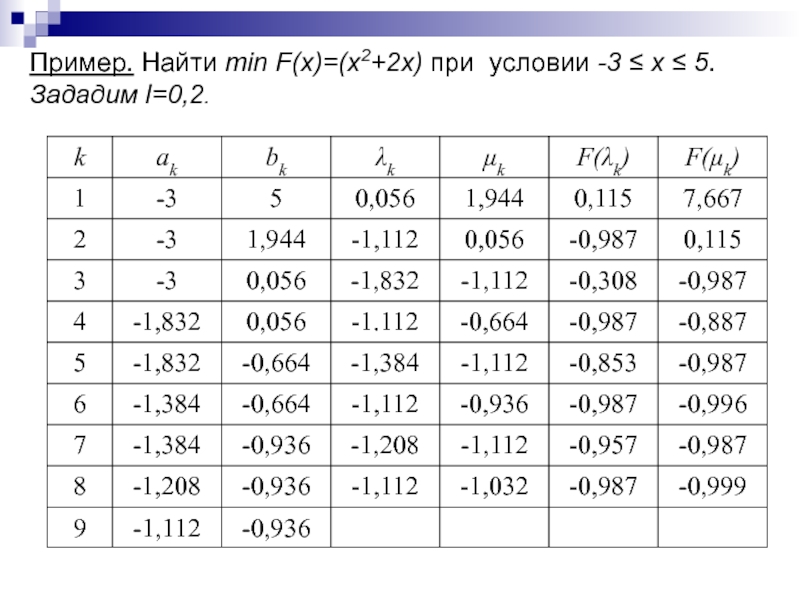
Слайд 209Пример. Найти min F(x)=(x2+2x) при условии -3 ≤ x ≤
5.
Зададим l=0,2.
Слайд 210Метод Гаусса-Зайделя (покоординатного спуска)
(xi)k+1= (xi)k ± λi
где (xi)k+1 -
новая координата по i-ой переменной;
(xi)k – текущая координата по
i-ой переменной;
λi - длина шага изменения координаты по i-ой переменной.
Критерий остановки поиска |F(Xk+1)-F(Xk)|<ε.
Слайд 211Градиент многомерной функции
Координаты точки при поиске минимума вычисляются по
выражению:
где λk - длина (параметр) шага на k-ой
итерации
вдоль антиградиента
Слайд 212Варианты остановки процесса поиска оптимума:
1. По разности значений целевой функции
2.
По величине нормы
3. По величине изменения шага
Слайд 213Пример. Найти минимум целевой функции градиентным
методом с постоянным шагом
F(X)=(x1-2)2+(
x1-2x2)2
Выбираем шаг λk=0,05. Начальная точка X1=[0;3]T
Слайд 214Метод наискорейшего спуска
F(Xk+1)=F(Xk-λkSk)=min F(λk)
λk>0
Sk=∇F(X);
Пример. minF(x1,x2)=2x12 + 4x23 –
3
∇F(X)=[ 4x1; 12x22]. Пусть точка Xk=[2,0;1,0], тогда
-∇F(X)=[ -8; -12]
F(Xk-λkSk)=2(2-8λ)2+4(1-12λ)3-3.
Необходимо найти λ, доставляющее минимум данной
функции.
Слайд 215Лекция 20. Решение задачи
условной оптимизации в
нелинейном программировании.
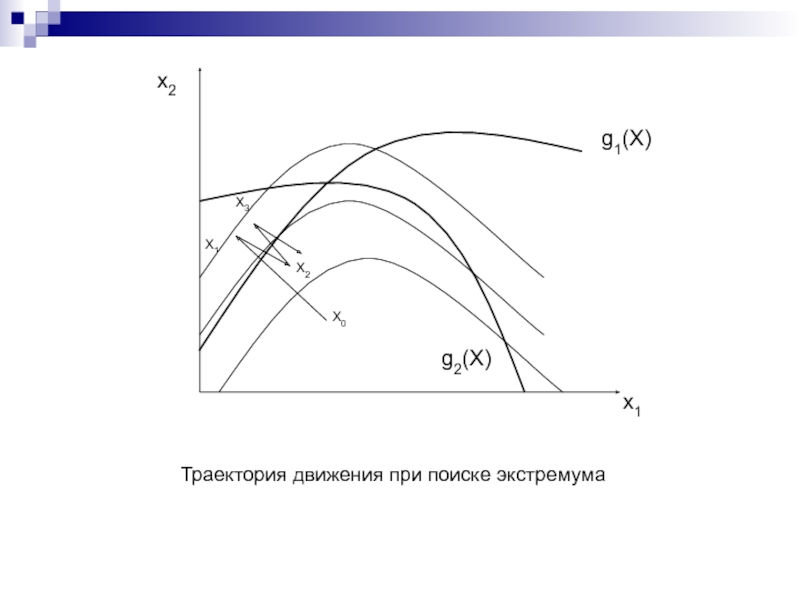
Слайд 216Использование градиентного метода при
наличии ограничений.
Рассмотрим задачу поиска минимума для
ограничений вида
gi(X) ≤ 0.
Если хотя бы одно из ограничений
нарушено, то дальнейший
поиск ведется следующим образом:
а) для всех gi(X), которые стали положительными, составляется
новый комплексный критерий
, где m – число нарушенных ограничений.
б) вычисляется grad H, так же, как и для F(X).
в) делается шаг в направлении -grad Н до тех пор, пока
все gi(X) не станут отрицательными (не войдем в ОДР).
Слайд 217Траектория движения при поиске экстремума
Слайд 218Методы штрафных функций.
Оптимизацию проводят по новому критерию
- штрафная функция,
r – параметр штрафа
Часто штрафная функция строится по следующему правилу
m
- число ограничений, f - некоторая функциональная зависимость.
Слайд 219В методах внешней точки
Штрафной параметр в этом методе
rk+1=αrk, α>1,
k
- номер решения задачи безусловной оптимизации.
Слайд 220В методах внутренней точки
rk+1=αrk, α
по величине штрафной функции,
по величине шага по хi.
Слайд 221Алгоритм методов штрафных функций. Пусть необходимо найти минимум F(X) при
ограничениях gi(X)≤ 0.
Шаг 1. При начальной точке Xk решают
задачу
Положить Xk+1 равным оптимальному решению этой задачи и перейти к шагу 2.
Шаг 2. Если
и
то остановиться. В противном случае rk+1=α rk, присвоить k=k+1 и перейти к шагу 1.
Выбрать ε1 > 0 и ε2 > 0
начальную точку X1
Выбрать параметр штрафа r1(можно принять равным единице) и коэффициент α (для метода барьерных поверхностей α=0,1; для метода внешней точки α=10).
Слайд 222Для метода внешней точки при наличии дополнительно
l ограничений в
виде равенств gj(X)=0, j=1,l
штрафная функция должна быть записана
в виде
Слайд 223Пример. Решить методом внешней точки следующую задачу.
при
В качестве метода безусловной
оптимизации будем
использовать классический метод.
x1=2x2
x1=2/3
Слайд 224Лекция 21. Формальное описание коммутационных схем. Методы и алгоритмы решения
задачи компоновки.
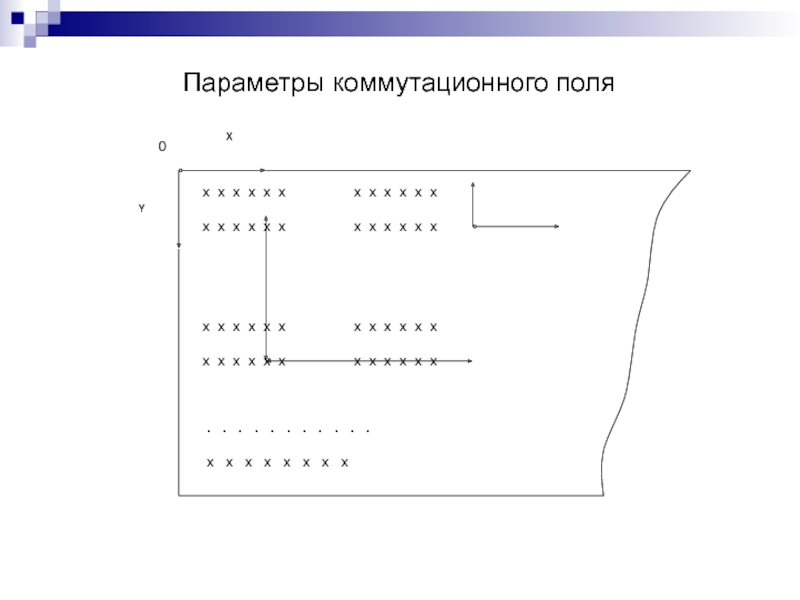
Слайд 225Математическая модель монтажно-коммутационного
пространства.
Электрическую схему интерпретируют ненаправленным
мультиграфом, в
котором каждому i-му конструктивному
элементу (модулю) ставят в соответствие вершину
мультиграфа хi, а электрическим связям схемы — его ребра uij
Требуется «разрезать» граф G(X, U) на отдельные куски
Gi(Xi, Ui) так, чтобы число ребер, соединяющих эти куски,
было минимальным
при
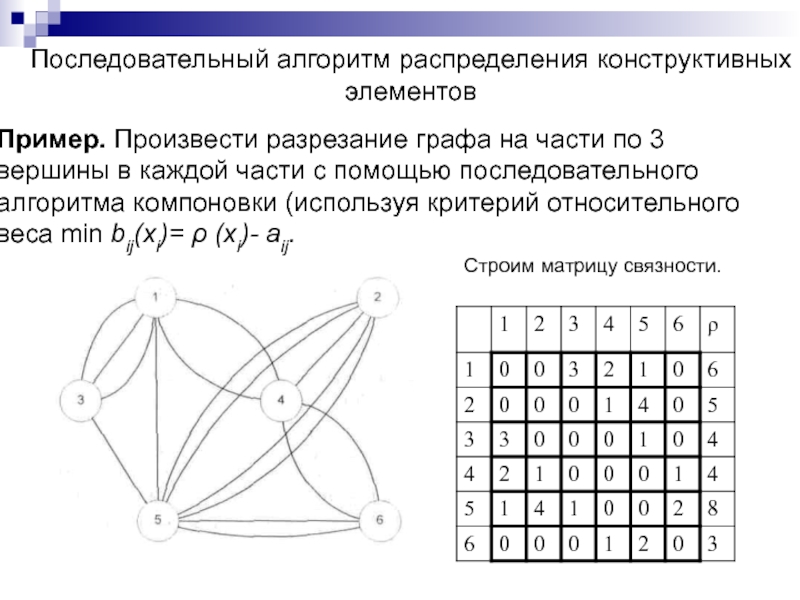
Слайд 226Последовательный алгоритм распределения конструктивных
элементов
Пример. Произвести разрезание графа на
части по 3
вершины в каждой части с помощью последовательного
алгоритма компоновки (используя критерий относительного
веса min bij(xi)= ρ (хi)- aij.
Строим матрицу связности.
Слайд 227Вычисляем вершину с самой большой максимальной
степенью. Это вершина 5.
Подбор
кандидатов на присоединение в единый кусок
производим по формуле: bij(xi)=
ρ (хi)- aij, где aij -число
связей i-той вершины с j-ой
b51=8 -1=7; b52=8 -4=4; b53=8 -1=7; b56=8 -2=6
Следовательно, объединяем 5 и 2 в один кусок
b521=5 -1=
4; b523=5 -1=4; b524=5 -1=4; b526=5 -2=3.
В один кусок с 5 и 2 объединяем вершину 6
Слайд 228Лекция 22.
Постановка задачи размещения конструктивных модулей на плате.
Классификация алгоритмов размещения.
Слайд 230Размещение элементов
Расстояние между соединяемыми элементами (выводами i и j)
можно определить одним из следующих способов:
Слайд 231Задано множество конструктивных элементов R={r1,r2,…,rn}
и множество связей между этими
элементами V={v1,v2,…,vp},
а также множество установочных мест (позиций) на
коммутационной
плате T={t1,t2,…,tk}. Найти такое
отображение множества R на множестве T, которое
обеспечивает экстремум целевой функции
где
– вес k-ой цепи, связывающей элементы i и j;
sk – число контактов, объединенных цепью;
N – число цепей схемы между i и j элементами.
Слайд 232Если необходимо, то можно учесть рассредоточение
элементов с точки зрения
тепловой или электромагнитной
совместимости следующим образом
Здесь с/ij – весовой коэффициент,
рассчитанный по предыдущему выражению, α - коэффициент теплоотдачи в реальной конструкции или коэффициент, учитывающий электромагнитную совместимость, Ei и Ej – мощности, рассеиваемые в компонентах i и j либо уровни напряженности электромагнитного поля, Eдоп – допустимый уровень мощности или напряженности двух рядом размещенных элементов.
Слайд 233Лекция 23.
Последовательный и итерационный алгоритмы размещения конструктивных модулей на
плате
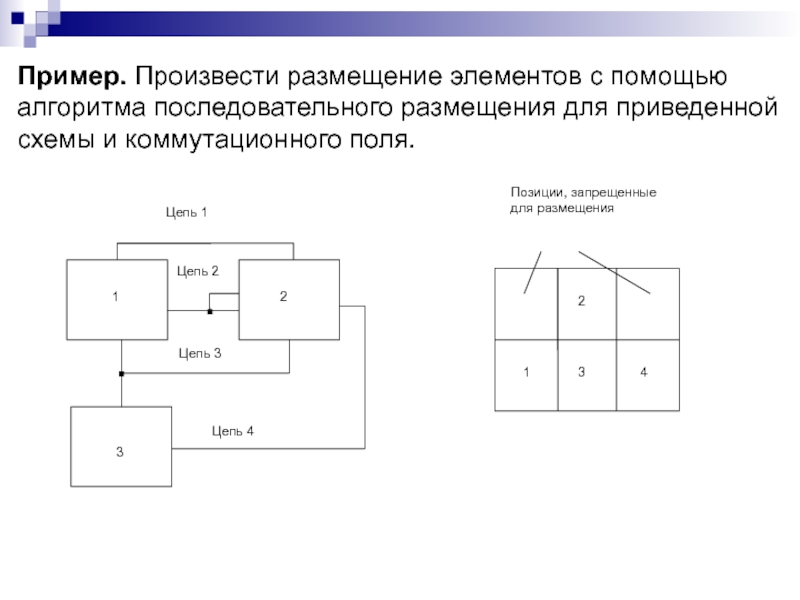
Слайд 234Пример. Произвести размещение элементов с помощью
алгоритма последовательного размещения для
приведенной
схемы и коммутационного поля.
Слайд 235Матрица относительных расстояний в ортогональной метрике
Вектор очередности позиций для
размещения 3;1;2;4
Вектор назначения элементов на позиции: 2;1;3
Решение на
1 позиции – первый элемент; на второй – третий элемент; на третей – второй элемент; четвертая позиция – пустая.
Слайд 236Итерационные алгоритмы размещения
В случае минимизации суммарной взвешенной длины
соединений формула
для расчета изменения значения
целевой функции при перестановке местами элементов
ri и rj , закрепленных в позициях tf и tg, имеет вид:
где p и h(p) – порядковый номер и позиция закрепления неподвижного элемента rp
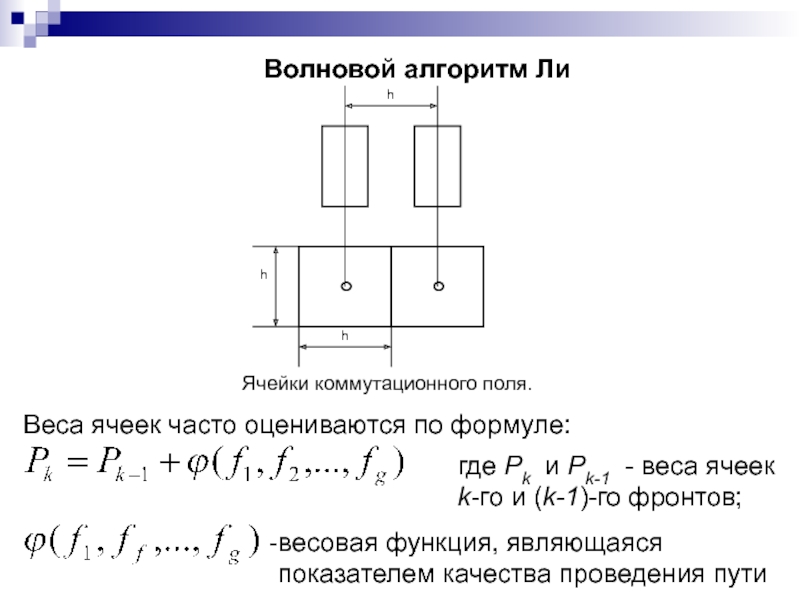
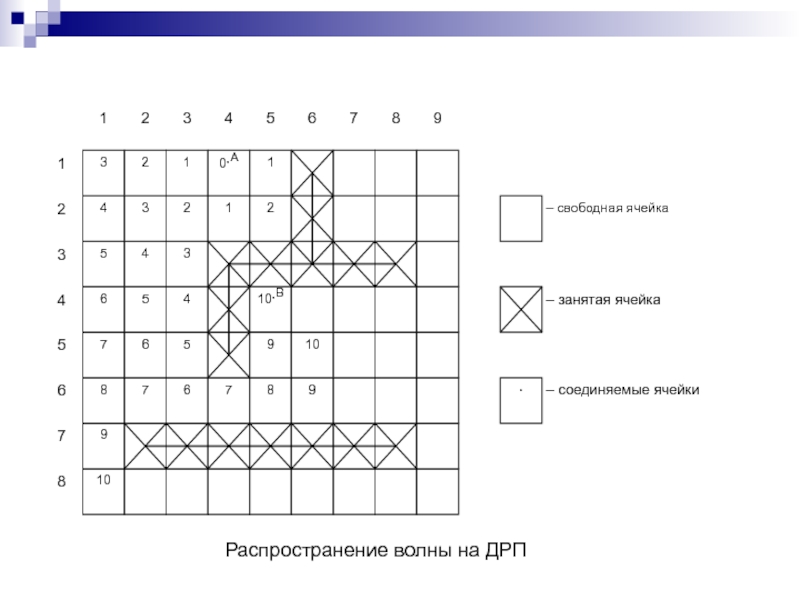
Слайд 238Волновой алгоритм Ли
Веса ячеек часто оцениваются по формуле:
где Pk
и Pk-1 - веса ячеек
k-го и (k-1)-го фронтов;
весовая
функция, являющаяся
показателем качества проведения пути
Слайд 241Лекция 25
Модифицированные волновые алгоритмы.
Лучевые алгоритмы трассировки
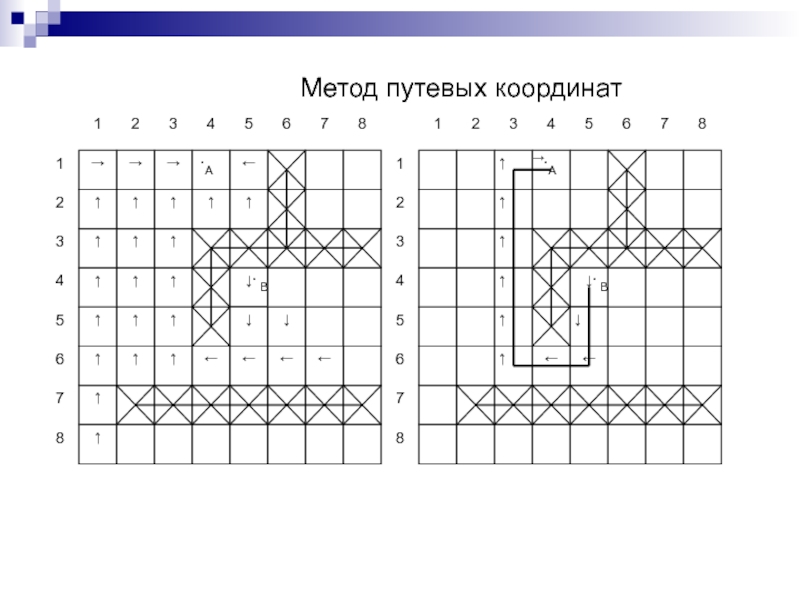
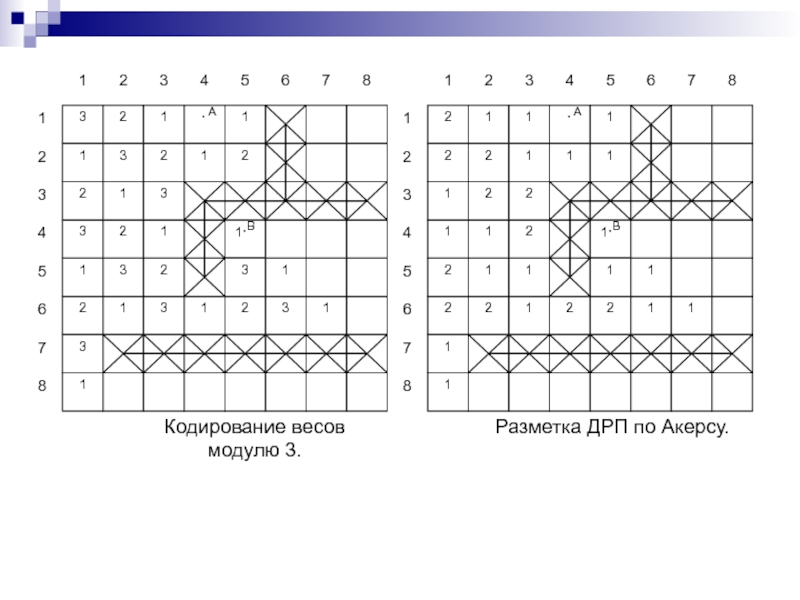
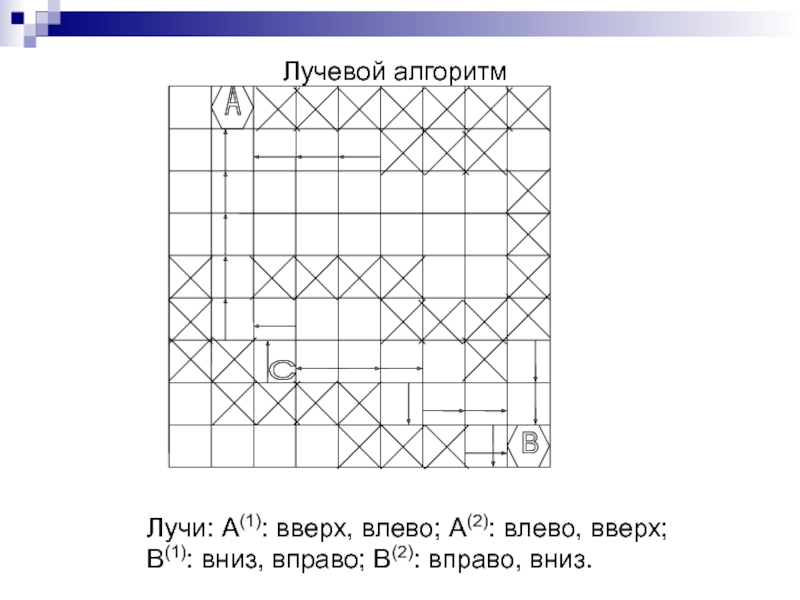
Слайд 244Лучевой алгоритм
Лучи: A(1): вверх, влево; A(2): влево, вверх;
B(1): вниз,
вправо; B(2): вправо, вниз.

























![Слайды Станкевич 2009.ppt Интерполяция данныхНа отрезке [a, b] заданы n + 1 точка xi = х0, х1, . . ., хn, которые называются Интерполяция данныхНа отрезке [a, b] заданы n + 1 точка xi = х0, х1, . . ., хn, которые называются узлами интерполяции, и значения некоторой функции](/img/thumbs/ebc2c33137de0a888a8895de933d5584-800x.jpg)





![Слайды Станкевич 2009.ppt Погрешность полиномиальной интерполяцииПредположим, что во всех точках х∈[a, b] функция f(x) имеет Погрешность полиномиальной интерполяцииПредположим, что во всех точках х∈[a, b] функция f(x) имеет (n+1) непрерывную производную.Тогда абсолютная ошибка интерполяции](/img/thumbs/a08559fe96380c777728ddff6fd10729-800x.jpg)
![Слайды Станкевич 2009.ppt Пример. Пусть требуется составить таблицу функции y=ln x на отрезке [1,10]. Пример. Пусть требуется составить таблицу функции y=ln x на отрезке [1,10]. Какой величины должен быть шаг h,](/img/thumbs/82dff3b6d585a8879c984e6623cc529d-800x.jpg)


























![Слайды Станкевич 2009.ppt Метод бисекцииПусть [a,b] - отрезок локализации. Предположим, что функция f(x) непрерывна Метод бисекцииПусть [a,b] - отрезок локализации. Предположим, что функция f(x) непрерывна на [a,b] и на концах принимает](/img/thumbs/ee8ec2e60f1de2f8e62a1cb51166e48f-800x.jpg)
![Слайды Станкевич 2009.ppt Шаг метода бисекцииПусть на k-ом шаге найден отрезок [ak,bk] такой, что f(ak)· f(bk) Шаг метода бисекцииПусть на k-ом шаге найден отрезок [ak,bk] такой, что f(ak)· f(bk)](/img/thumbs/b7f3ff4babac1fce7905c73217b5d6b7-800x.jpg)








![Слайды Станкевич 2009.ppt Численное интегрированиеЗадача численного интегрирования состоит в нахожденииприближенного значения интеграла:В качестве приближенного Численное интегрированиеЗадача численного интегрирования состоит в нахожденииприближенного значения интеграла:В качестве приближенного значения интеграла L[f] рассмотрим следующее: где](/img/thumbs/daac60122fb630af0a0d7f88a1298f0a-800x.jpg)
![Слайды Станкевич 2009.ppt Формула прямоугольников.Заменим на отрезке [xi-1, xi] функцию y=f(x) полиномом нулевой степениξi Формула прямоугольников.Заменим на отрезке [xi-1, xi] функцию y=f(x) полиномом нулевой степениξi = (xi+xi-1 ) /2,Для случая учета](/img/thumbs/aa6714c1e76c2687d0c1382a13958868-800x.jpg)
































![Слайды Станкевич 2009.ppt С математической точки зрения численное решение на отрезке [a, b] задачи С математической точки зрения численное решение на отрезке [a, b] задачи Коши для дифференциального уравнения первого порядкаy'](/img/thumbs/2f598321d8b9c68b6dff6ed15073a9a2-800x.jpg)























































![Слайды Станкевич 2009.ppt Метод ветвей и границНа основании полученного решения составляются дополнительные к исходной Метод ветвей и границНа основании полученного решения составляются дополнительные к исходной задаче ограниченияи где [xj] - целая](/img/thumbs/a2f57e4ac148c52c306b75e64ebb8c64-800x.jpg)

![Слайды Станкевич 2009.ppt Метод золотого сечения. Предварительный этап. Выбрать допустимую конечную длину интервала неопределенности Метод золотого сечения. Предварительный этап. Выбрать допустимую конечную длину интервала неопределенности l>0. Пусть [a1,b1] - начальный интервал](/img/thumbs/8f142b6870092e52b3b1683eac0caefb-800x.jpg)



![Слайды Станкевич 2009.ppt Пример. Найти минимум целевой функции градиентным методом с постоянным шагомF(X)=(x1-2)2+( x1-2x2)2Выбираем Пример. Найти минимум целевой функции градиентным методом с постоянным шагомF(X)=(x1-2)2+( x1-2x2)2Выбираем шаг λk=0,05. Начальная точка X1=[0;3]T](/img/thumbs/42ded7388144404dd0037c3f155bfcd0-800x.jpg)
![Слайды Станкевич 2009.ppt Метод наискорейшего спуска F(Xk+1)=F(Xk-λkSk)=min F(λk) λk>0Sk=∇F(X); Пример. minF(x1,x2)=2x12 + 4x23 – 3∇F(X)=[ Метод наискорейшего спуска F(Xk+1)=F(Xk-λkSk)=min F(λk) λk>0Sk=∇F(X); Пример. minF(x1,x2)=2x12 + 4x23 – 3∇F(X)=[ 4x1; 12x22]. Пусть точка Xk=[2,0;1,0], тогда](/img/thumbs/2511fd56a1bba94e31853b70c67a0cea-800x.jpg)