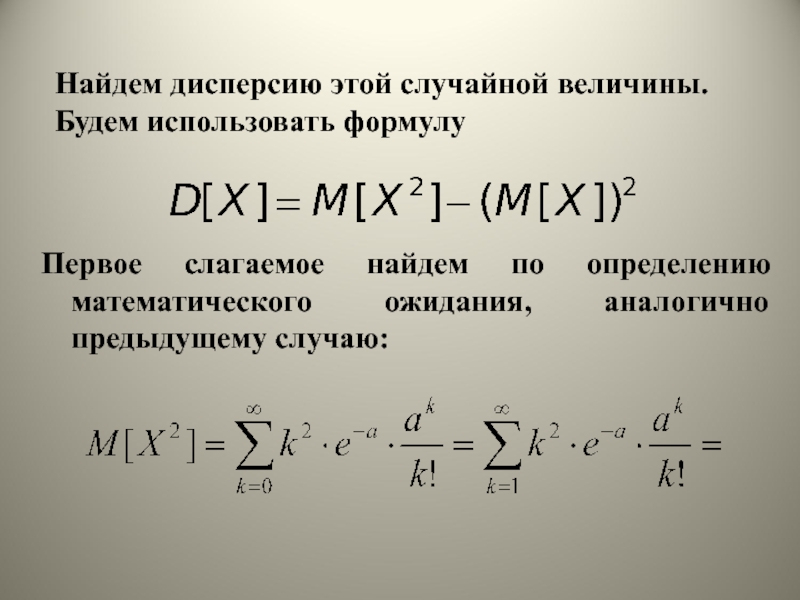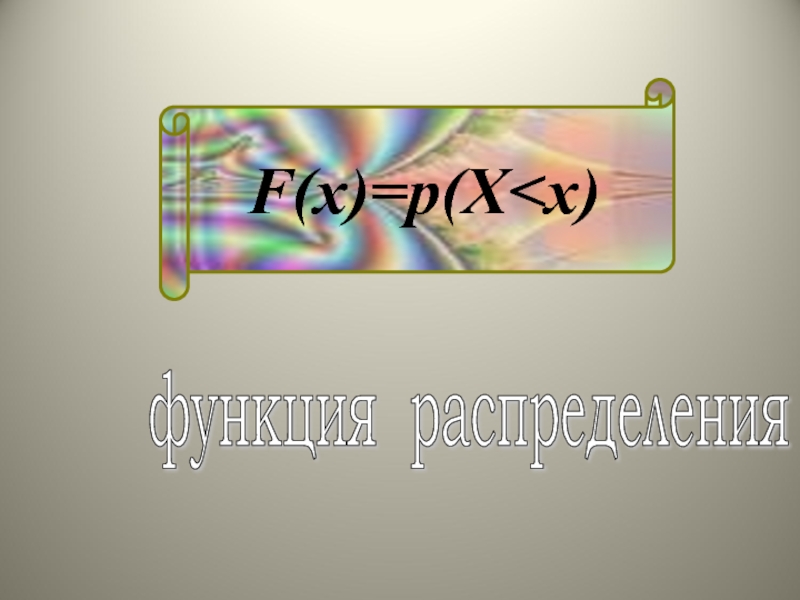Слайд 1Лекция
Тема: Случайные величины и их законы распределения
Учебные вопросы:
Понятие случайной величины.
Распределение случайной величины.
Математическое ожидание. Дисперсия, стандартное отклонение.
Некоторые распределения дискретной случайной
величины.
Функция распределения дискретной случайной величины.
Слайд 2Случайная величина
Случайной величиной называется переменная величина, значения которой зависят от
случая. Примеры случайных величин: число попаданий в мишень при данном
числе выстрелов; число очков, выпадающее при бросании игральной кости. Обозначаем X, а ее значения x.
Дискретная
Случайная величина, возможные значения которой можно перенумеровать. При этом число значений может быть конечным или
бесконечным
Непрерывная
Случайная величина, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины – бесконечно
Слайд 3Дискретная случайная величина
Дискретная случайная величина принимает конечное или счетное количество
значений. Счетное количество может быть бесконечным, но, тем не менее,
может быть подсчитано при помощи определенной процедуры.
ПРИМЕР: Счетными являются, например, целые числа.
Число новорожденных
0
2
1
3
4
5
6
Слайд 4Непрерывная случайная величина
Непрерывная случайная величина, в противоположность дискретной, принимает бесконечное
количество значений из определенного непрерывного множества на числовой прямой. Множество
значений непрерывной случайной величины несчетно.
ПРИМЕР: Срок службы лампочки.
0
6
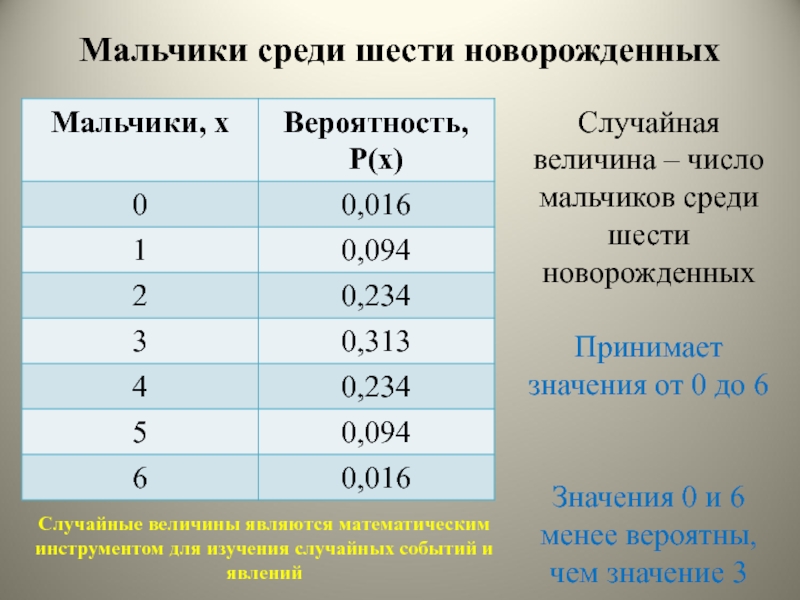
Слайд 5Мальчики среди шести новорожденных
Случайная величина – число
мальчиков среди шести новорожденных
Принимает
значения от 0 до 6
Значения 0 и 6 менее вероятны,
чем
значение 3
Случайные величины являются математическим инструментом для изучения случайных событий и явлений
Слайд 6Распределение дискретной случайной величины
Для характеристики случайной величины нужно знать совокупность
возможных значений этой величины, а также вероятности, с которыми эти
значения могут появиться. Эти данные образуют закон распределения случай-
ной величины. Закон распределения дискретной случайной величины X может быть задан в виде графика, формулы или таблицы, первая строка которой содержит возможные значения xi, а вторая – вероятности pi:
Таблица задает закон распределения случайной
величины
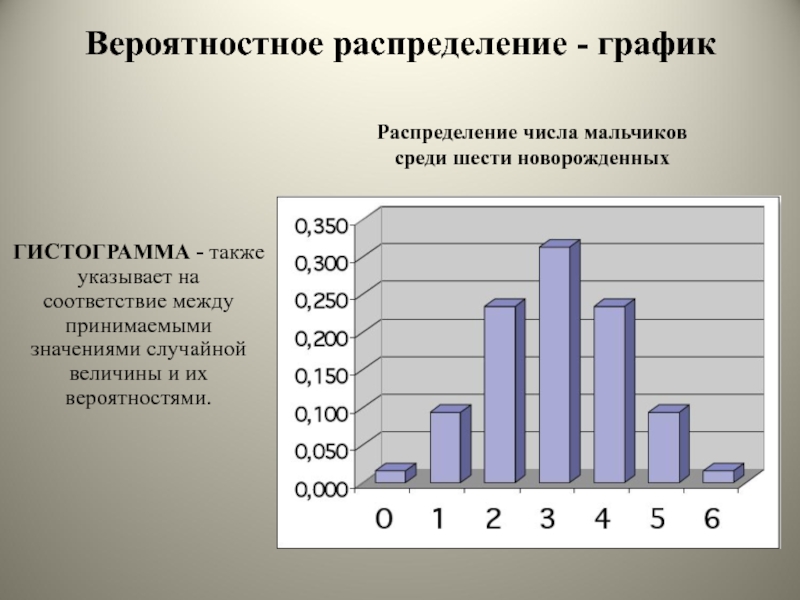
Слайд 7Вероятностное распределение - график
Распределение числа мальчиков среди шести новорожденных
ГИСТОГРАММА -
также
указывает на
соответствие между
принимаемыми
значениями случайной
величины и их
вероятностями.
Слайд 8Вероятностное распределение - формула
Вероятностное распределение случайной величины может быть задано
аналитически – формулой
Пример. Формула для нахождения вероятности k мальчиков среди
6 новорожденных:
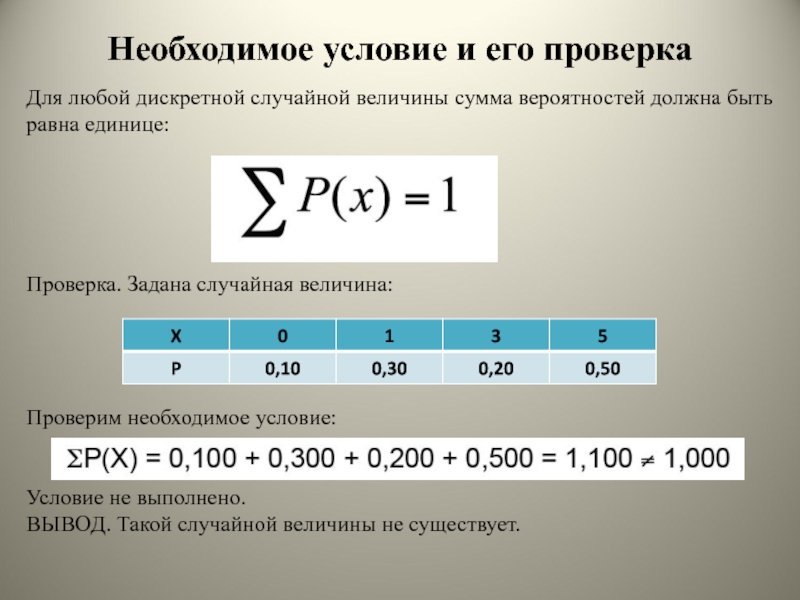
Слайд 9Необходимое условие и его проверка
Для любой дискретной случайной величины сумма
вероятностей должна быть равна единице:
Проверка. Задана случайная величина:
Проверим необходимое
условие:
Условие не выполнено.
ВЫВОД. Такой случайной величины не существует.
Слайд 12Математическое ожидание
Математическим ожиданием дискретной случайной величины называется сумма произведений всех
ее возможных значений на их вероятности
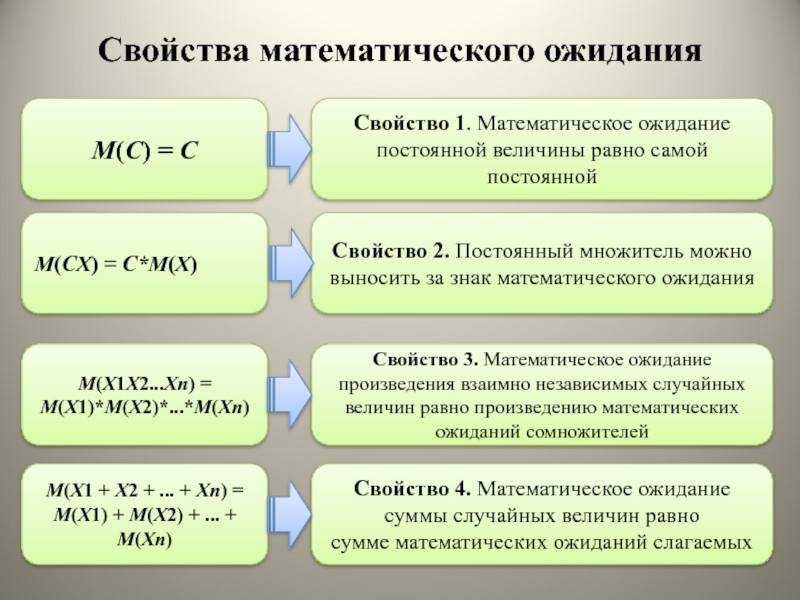
Слайд 13Свойства математического ожидания
M(C) = C
Свойство 1. Математическое ожидание постоянной величины
равно самой постоянной
M(CX) = C*M(X)
Свойство 2. Постоянный множитель можно выносить
за знак математического ожидания
M(X1 + X2 + ... + Xn) = M(X1) + M(X2) + ... + M(Xn)
Свойство 4. Математическое ожидание суммы случайных величин равно
сумме математических ожиданий слагаемых
M(X1X2...Xn) = M(X1)*M(X2)*...*M(Xn)
Свойство 3. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей
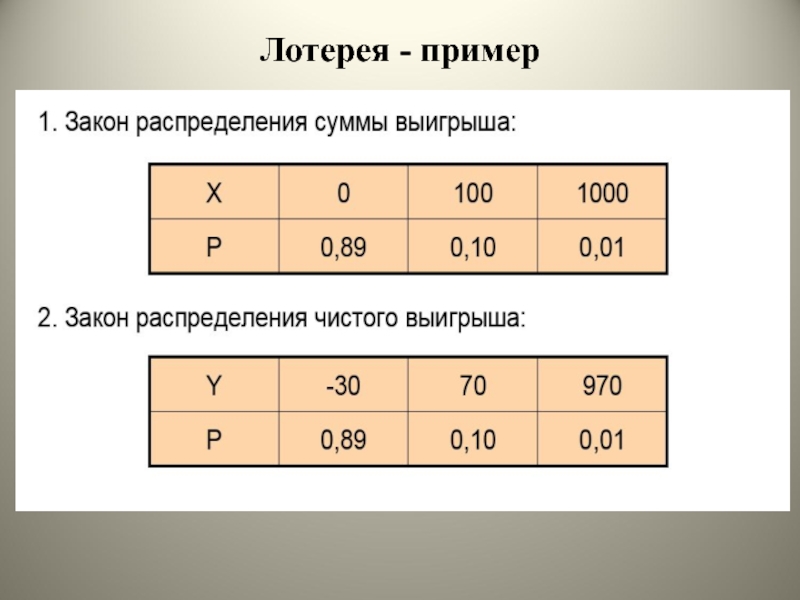
Слайд 14Математическое ожидание выигрыша
Слайд 15Математическое ожидание выигрыша
Слайд 16Интерпретация
Такую лотерею можно считать несправедливой, поскольку в ней
предусмотрен выигрыш организатора.
Если
математическое ожидание равно -10, это означает, что в
среднем каждый участник
проигрывает -10 руб.
Если бы математическое ожидание было равно нулю, то выигрыши одних участников брались бы из проигрышей других участников.
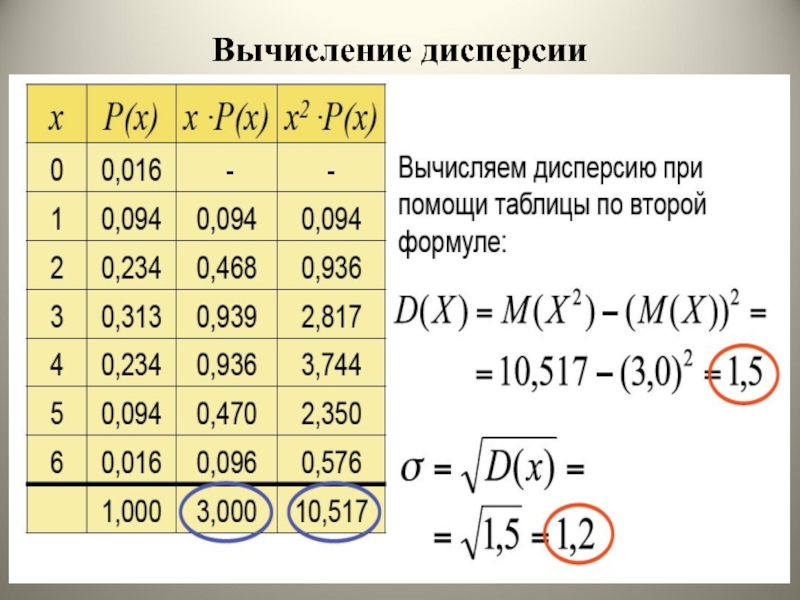
Слайд 17Дисперсия
Дисперсией случайной величины X называется математическое ожидание квадрата отклонения случайной
величины от ее математического ожидания:
D(X) = M([X – M(X)]2).
Дисперсию удобно
вычислять по формуле
D(X) = M(X2) – [M(X)]2.
Слайд 18Свойства дисперсии
D(C) = 0
Свойство 1. Дисперсия постоянной равна нулю
D(CX) =
C2*D(X)
Свойство 2. Постоянный множитель можно выносить за знак дисперсии,
предварительно возведя
в квадрат
D(X1 + X2 + ... + Xn) = D(X1) + D(X2) + ... + D(Xn)
Свойство 3. Дисперсия суммы независимых случайных величин равна сумме
дисперсий слагаемых
Слайд 20Вычисление дисперсии чистого выигрыша
Слайд 21Вычисление стандартного отклонения
Слайд 23Некоторые законы распределения дискретных случайных величин
Биномиальное распределение
Геометрическое распределение
Распределение
Пуассона
Биномиальное распределение
Слайд 24
где q=1-p.
Случайная величина Х называется распределенной
по биномиальному закону с
параметрами
n,p >0, если Х принимает значения: 0,1,2,…n
и вероятность
того, что случайная величина
примет значение X=m находится
по формуле Бернулли:
Биномиальное распределение
Слайд 25Случайную величину Х, распределенную по биномиальному закону, можно трактовать следующим
образом:
Рассмотрим событие А, которое происходит в опыте с вероятностью р
и не происходит с вероятностью q=1-p. Производится серия из n опытов в одинаковых условиях и независимо друг от друга. Случайная величина Х - сколько раз событие А произошло в данной серии опытов.
Слайд 26Составить ряд распределения величины, распределенной по биномиальному закону с параметрами
n=4, р=1/3.
Пример применения биномиального распределения
Слайд 27Производится серия из n=4 опытов. Случайная величина Х - число
опытов, в которых может произойти событие А, может принимать значения
0, 1, 2, 3, 4.
Соответствующие вероятности находятся по формуле Бернулли при n=4, p=1/3, q=1-1/3=2/3.
Вероятность того, что событие А не произойдет ни в одном опыте (m=0):
Решение примера
Слайд 28Вероятность того, что событие А произойдет
в одном опыте
(m=1):
Аналогично находим вероятности того, что это событие произойдет в двух
(m=2), в трех (m=3) и в четырех (m=4) опытах:
Слайд 29Можно убедиться, что суммарная вероятность действительно равна 1.
Таким образом,
ряд распределения случайной величины Х будет выглядеть так:
Слайд 30Найдем математическое ожидание случайной величины, распределенной по биномиальному закону.
Х -
число опытов в серии из n, в которых произошло событие
А.
Введем для каждого i=1,2…n случайную величину Zi .
Пусть Zi принимает всего два значения: 1 - если событие А произойдет в i-ом опыте и 0 - если событие А не произойдет в i-ом опыте.
Тогда событие Х выразится через сумму событий Zi :
Х= Z1 +Z2 +…+Zn
Слайд 31Тогда математическое ожидание случайной величины Х:
M[X]=M[Z1]+M[Z2]+…+M[Zn]
Найдем математическое ожидание Zi
Ряд распределения
Zi имеет вид:
Тогда M[Zi ]=p и M[X]=np.
Слайд 32Найдем дисперсию случайной величины Zi
Так как случайные величины Zi независимы,
то
Таким образом, для случайной величины,
распределенной по биномиальному закону,
Слайд 34Некоторые законы распределения дискретных случайных величин
Биномиальное распределение
Геометрическое распределение
Распределение
Пуассона
Геометрическое распределение
Слайд 35где q=1-p.
Случайная величина Х называется распределенной
по закону геометрической
прогрессии
с параметром р>0, если она может
принимать значения 1,2,3…,k,…
и вероятность
того, что Х примет значение, равное k,
находится по формуле:
Геометрическое распределение
Слайд 36Рассмотрим событие А, которое происходит в опыте с вероятностью р.
Проводится серия опытов в одинаковых условиях и независимо друг от
друга до тех пор, пока не случится событие А.
Число опытов и будет случайной величиной Х, распределенной по закону геометрической прогрессии.
Данное распределение можно трактовать следующим образом.
Слайд 37Можно показать, что математическое ожидание и дисперсия такой случайной величины
будут определяться выражениями:
Слайд 38В автосалоне покупатели выбирают
машины. Как правило, первые несколько
автомобилей
отвергаются, пока покупатель
не найдет подходящий. Найти ряд распределения
случайной
величины - числа отвергнутых
автомобилей, если вероятность того,
что покупателю понравится машина равна 1/5.
Пример применения геометрического распределения
Слайд 39Аналогично найдем, что машина будет куплена со второго и третьего
раза:
р=1/5, q=1-1/5=4/5
Тогда вероятность, что клиент купит машину с первого
раза будет
Решение примера
Слайд 40Тогда ряд распределения этой случайной величины будет иметь вид:
Тогда в
общем, вероятность того, что машина будет куплена с k -го
раза будет:
Слайд 42Некоторые законы распределения дискретных случайных величин
Биномиальное распределение
Геометрическое распределение
Распределение
Пуассона
Распределение Пуассона
Слайд 43
Случайная величина Х называется распределенной
по закону Пуассона с параметром
a>0,
если она может принимать значения
0, 1, 2,…,k,… и
вероятность того, что она
примет значение Х=k находится по формуле:
Распределение Пуассона
Слайд 44Найдем математическое ожидание и дисперсию случайной величины, распределенной по закону
Пуассона.
Распишем математическое ожидание по определению:
Первый член этой суммы равен нулю,
поэтому суммирование можно начать с k=1:
Слайд 45Вынесем a за знак суммы и переобозначим n-1=m:
Полученная сумма представляет
собой разложение в ряд функции ea:
Тогда:
Таким образом, параметр a имеет
смысл математического ожидания.
Слайд 46Найдем дисперсию этой случайной величины.
Будем использовать формулу
Первое слагаемое
найдем по определению математического ожидания, аналогично предыдущему случаю:
Слайд 47Вынесем a за знак суммы и сократим одно k:
Переобозначим k-1=m:
Разобьем
на две суммы:
Слайд 48Сумму в первом слагаемом мы уже считали при нахождении математического
ожидания. Она равна a.
Теперь находим саму дисперсию:
Таким образом, и
дисперсия случайной величины, распределенной по закону Пуассона, тоже равна параметру a.
Сумма во втором слагаемом снова представляет
разложение экспоненты в ряд.
Слайд 49При работе ЭВМ время от времени возникают
сбои. Среднее число
сбоев за сутки равно 1.5.
Считая, что число сбоев на
любом участке
времени распределено по закону Пуассона,
найти вероятности событий:
А - за 2 суток не будет ни одного сбоя;
В - в течение суток произойдет хотя бы один
сбой;
С - за неделю произойдет не менее трех сбоев.
Пример применения геометрического распределения
Слайд 50Чтобы воспользоваться распределением Пуассона нужно определить параметр a.
Так как
он равен математическому ожиданию этой величины, то он имеет смысл
среднего числа сбоев, произошедших за данный промежуток времени.
Среднее число сбоев за двое суток равно
1.
Решение примера
Слайд 51 Так как находится вероятность того, что за 2 суток
не произойдет ни одного сбоя, то k=0. Тогда искомая вероятность
будет равна:
2.
Чтобы найти вероятность того, что за сутки произойдет хотя бы один сбой, нужно перейти к вероятности противоположного события: за сутки не произойдет ни одного сбоя.
Слайд 52Вероятность этого события снова находим по формуле Пуассона при a=1.5
и k=0:
Тогда искомая вероятность будет:
Слайд 53Найдем вероятность того, что за неделю произойдет не менее 3
сбоев.
Противоположное событие: за неделю произойдет не более двух сбоев.
Это значит, произойдет 0, 1 или 2 сбоя.
Соответствующие вероятности находятся при k=0, k=1, k=2 и a=10.5.
Тогда:
3.
Слайд 55
Биномиальное распределение и распределение Пуассона связаны: распределение Пуассона является предельным
для биномиального.
Если случайная величина Х распределена по
биномиальному закону,
и число опытов
n - велико, а вероятность события в
каждом опыте р мала, то биномиальное
распределение можно приближенно заменить
пуассоновским при a=np:
Слайд 56По цели производится 50 независимых
выстрелов. Вероятность попадания в цель
при одном выстреле равна 0.04.
Используя предельное свойство
биномиального распределения,
найти
вероятность того, что в цель попадет
один снаряд.
Пример применения распределения Пуассона
Слайд 57Найдем параметр a распределения Пуассона:
Событие А - попадание при одном
выстреле.
Вероятность р(А)=0.04. Всего производится серия таких выстрелов: n=50.
Так
как р достаточно мало, а n - велико, биномиальное распределение приближенно можно заменить распределением Пуассона.
Решение примера
Слайд 58Тогда вероятность р1,50 того, что из 50-ти выстрелов будет одно
попадание по формуле Пуассона будет:
Слайд 59Функция распределения - самая универсальная характеристика случайной величины. Она может
быть определена как для дискретных, так и для непрерывных случайных
величин.
Введем новую характеристику случайных величин - функцию распределения и рассмотрим ее свойства.
Рассмотрим вероятность того, что СВ Х примет значение, меньшее, чем х, т.е. Р(Х<х),
Функция распределения случайной величины
Слайд 611
Функция распределения является неубывающей функцией своего аргумента, т.е. если
Свойства функции
распределения
Слайд 622
На минус бесконечности функция
распределения равна нулю:
Слайд 633
На плюс бесконечности функция
распределения равна единице:
Слайд 64
Проиллюстрируем эти свойства с помощью геометрической интерпретации.
Рассмотрим случайную величину
Х как случайную точку на оси х, которая в результате
опыта может принять то или иное положение.
Тогда функция распределения есть вероятность того, что эта случайная точка Х окажется левее точки х.
Слайд 65
Если неограниченно перемещать точку х влево по оси абсцисс (устремлять
х к минус бесконечности), то тогда попадание точки Х еще
левее становится невозможным событием, вероятность которого равна нулю.
Будем увеличивать х, т.е. перемещать точку х вправо.
При этом, вероятность того, что случайная точка Х попадет левее точки х не может уменьшится.
Поэтому функция распределения с возрастанием аргумента убывать не может.
Слайд 66
Аналогично, перемещая х вправо до бесконечности, получаем, что попадание точки
Х вправо от х становится достоверным событием, вероятность которого равна
1.
График функции распределения F(x) представляет собой график неубывающей функции, значения которой находятся в пределах от 0 до 1, причем в отдельных точках функция может иметь разрывы.
Слайд 67
где неравенство под знаком суммы означает, что суммирование ведется по
всем значениям хi которые меньше х.
Если задана дискретная случайная величина,
то по ее ряду распределения можно построить функцию распределения.
Слайд 68
Рассмотрим вероятность того, что случайная величина примет значение в пределах
от α до β:
Пусть событие А заключается в том, что
случайная величина Х примет значение, меньшее β: Х< β,
Событие В заключается в том, что Х< α
Событие С состоит в попадании случайной величины Х в интервал от α до β. Тогда искомая вероятность будет вероятностью события С:
Слайд 69
Тогда А=В+С.
По теореме о сложении вероятностей имеем:
Используя определение функции распределения
F(x):
Слайд 70
ВЕРОЯТНОСТЬ ПОПАДАНИЯ СВ НА ЗАДАННЫЙ ИНТЕРВАЛ
Слайд 71Производится серия из 4 опытов, в каждом
из которых может
появится событие А с
вероятностью 0.3. Случайная величина
Х –
число появлений события А
в опытах. Построить функцию
распределения случайной величины Х.
Пример
Слайд 72Случайная величина Х может принять 5 значений:
0, 1, 2,
3, 4.
Чтобы построить ее ряд распределения, найдем вероятности каждого
из этих значений по формуле Бернулли при р=0.3 и q=1-0.3=0.7 :
Решение примера
Слайд 73Тогда ряд распределения случайной величины будет выглядеть следующим образом:
Построим функцию
распределения этой случайной величины.
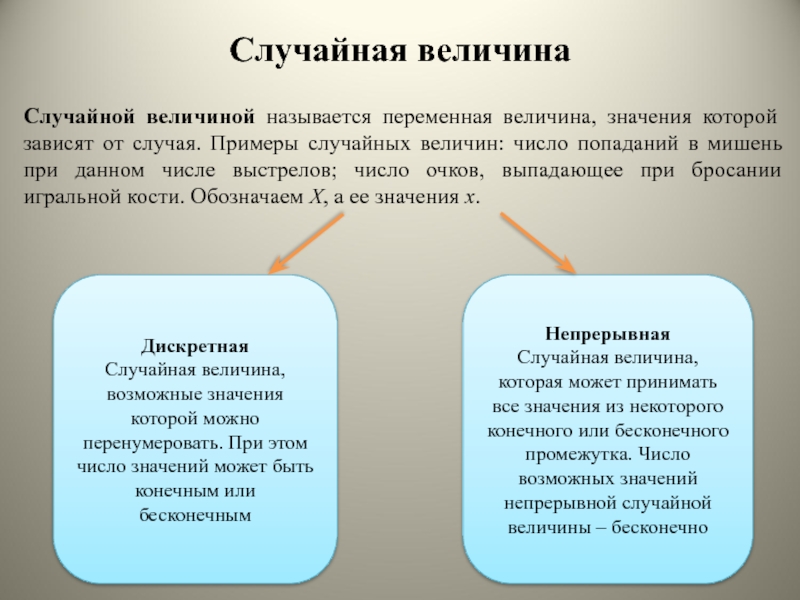
Слайд 74Так как случайная величина Х дискретна, то функция распределения будет
меняться скачкообразно, причем величина скачка (разрыва) будет равна вероятности данного
значения.
Найдем функцию распределения на каждом из промежутков Х :
1
2
3
Слайд 754
5
6
По найденным значениям строим функцию распределения.






















![Случайная величина и законы распределения Тогда математическое ожидание случайной величины Х:M[X]=M[Z1]+M[Z2]+…+M[Zn]Найдем математическое ожидание ZiРяд распределения Zi Тогда математическое ожидание случайной величины Х:M[X]=M[Z1]+M[Z2]+…+M[Zn]Найдем математическое ожидание ZiРяд распределения Zi имеет вид:Тогда M[Zi ]=p и M[X]=np.](/img/thumbs/d5c71f066f44fa885ffe6e5cf6bb168a-800x.jpg)