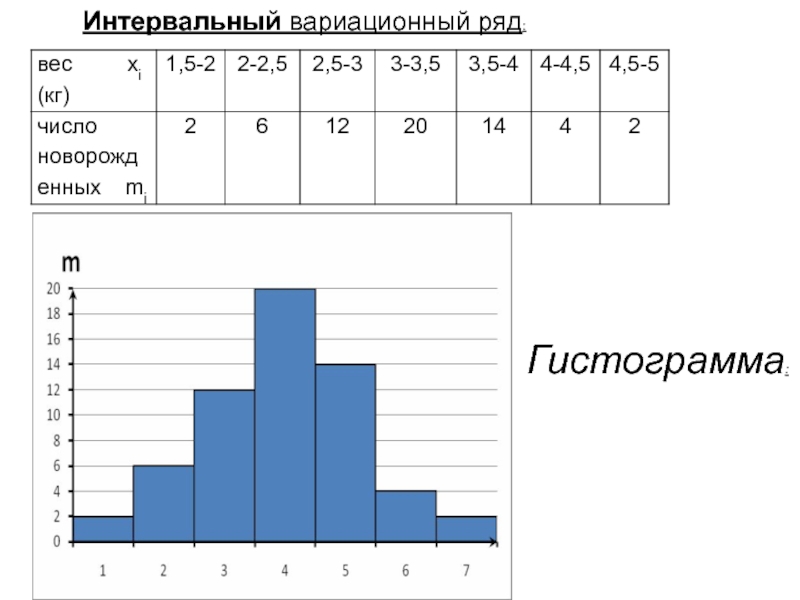
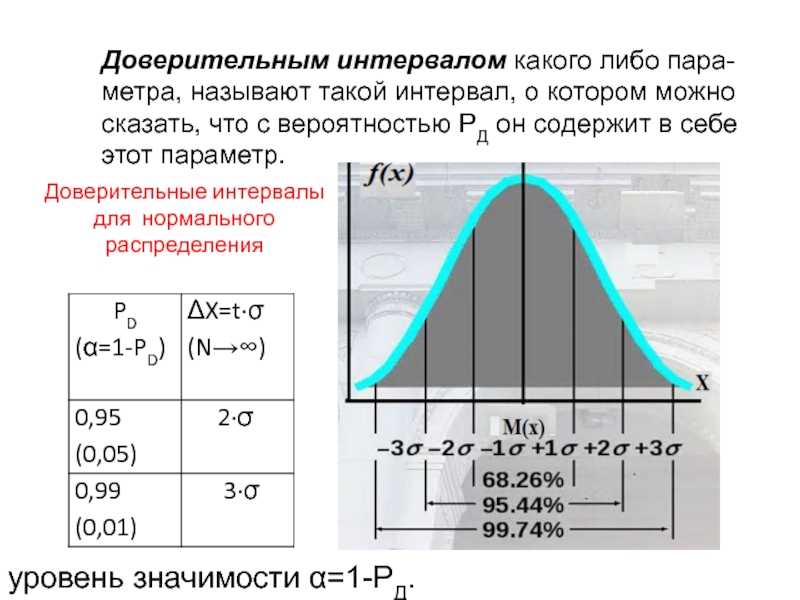
в зависимости от случайных обстоятельств.
.Дискретная случайная величина (точечная) принимает отдельные
числовые значения (кубик: 1,2,3,4,5,6)Непрерывная случайная величина принимает любые значения из
некоторого интервала
(рост студентов).


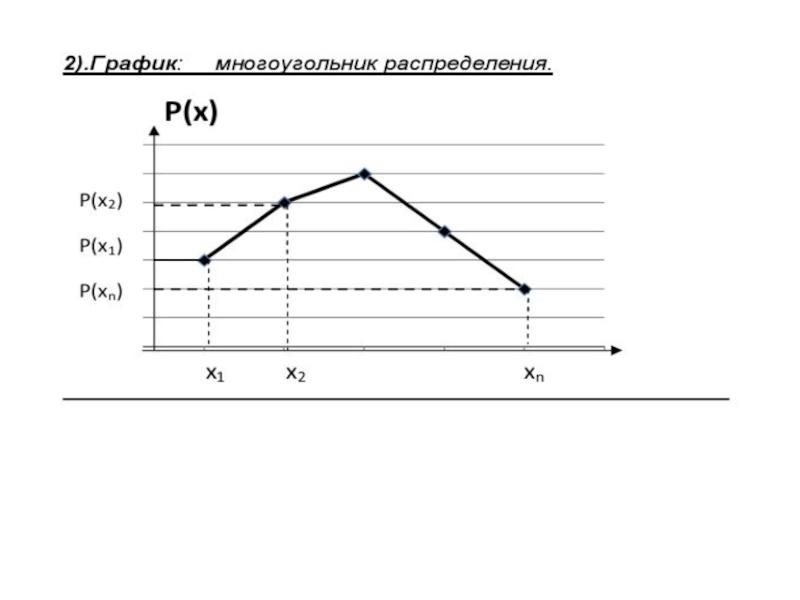




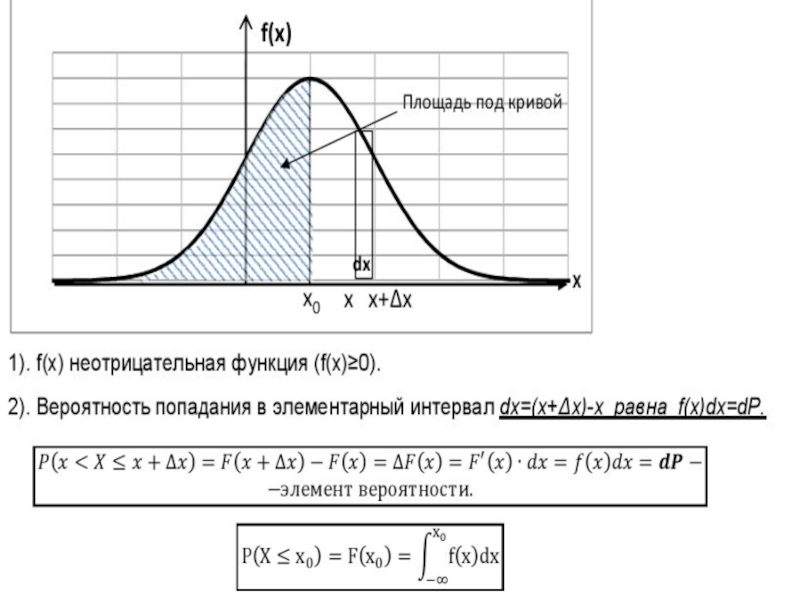










![Случайная величина Основные законы распределения непрерывной случайной величины1.Равномерное или прямоугольное распределение.Случайная величина называется Основные законы распределения непрерывной случайной величины1.Равномерное или прямоугольное распределение.Случайная величина называется равномерно распределённой на интервале [c,d], если](/img/thumbs/6a5866ff433573eb1b89474103cff929-800x.jpg)

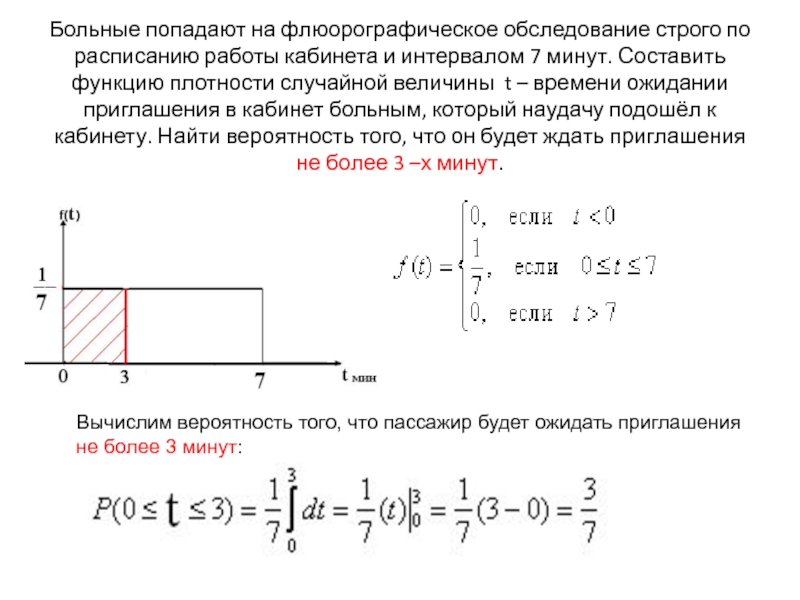
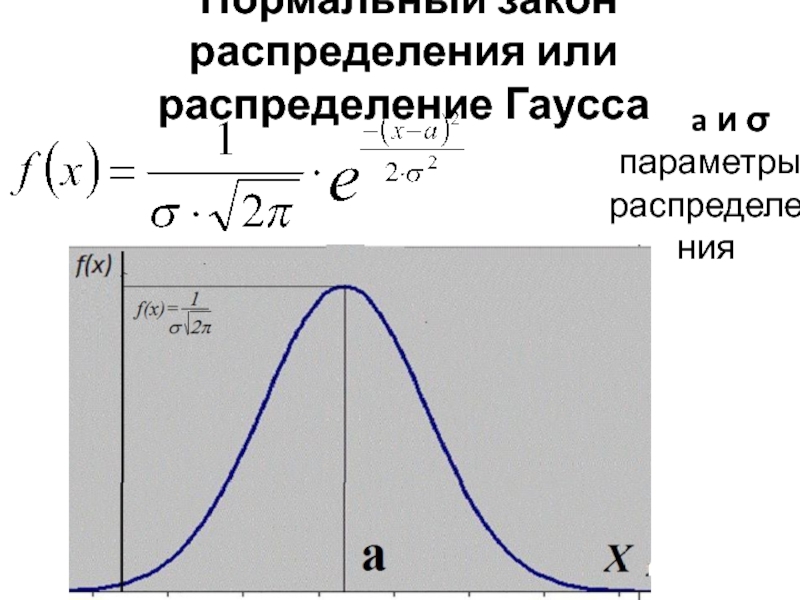
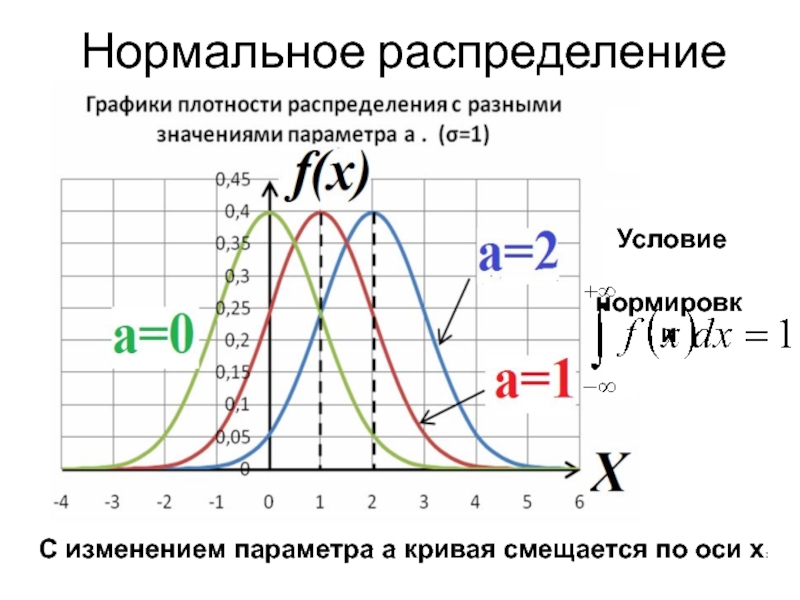



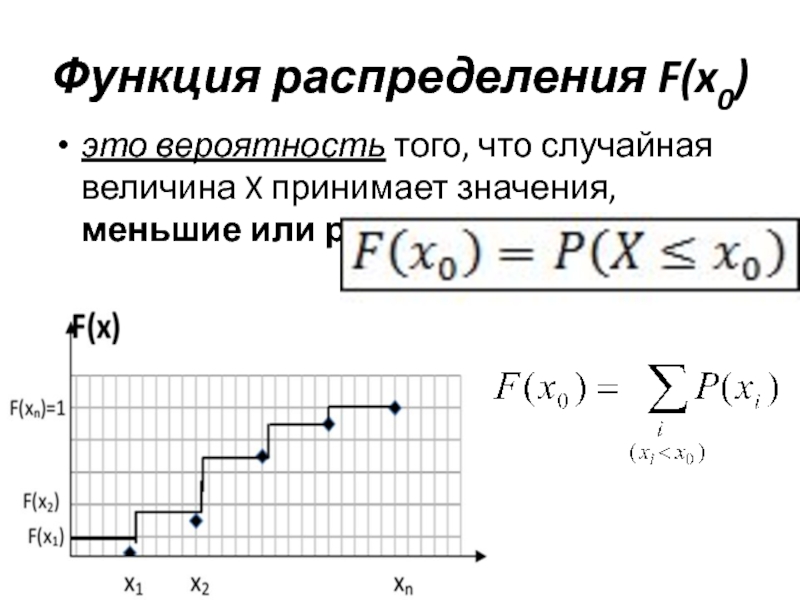
![Случайная величина Вероятность попадания значений случайной величины в интервал [a.b] Вероятность попадания значений случайной величины в интервал [a.b]](/img/thumbs/6b8410239b5ab51d9da16b101cc47454-800x.jpg)