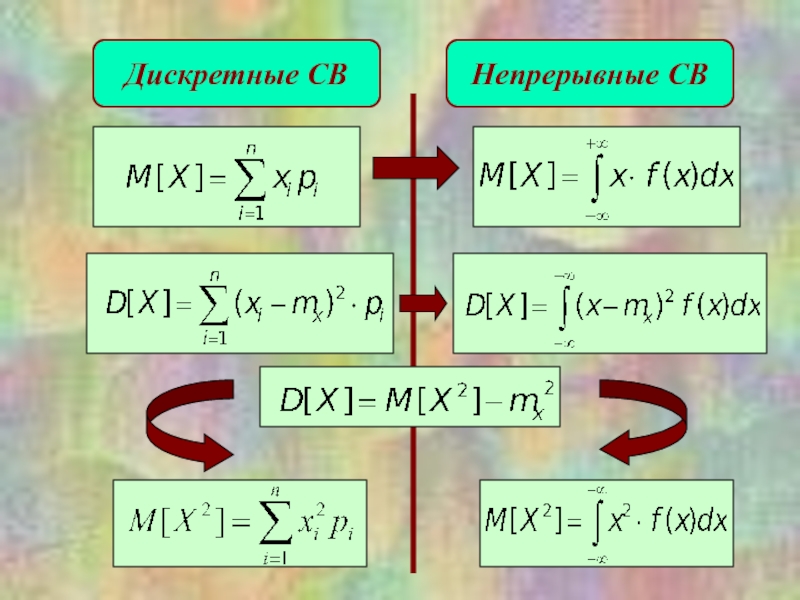
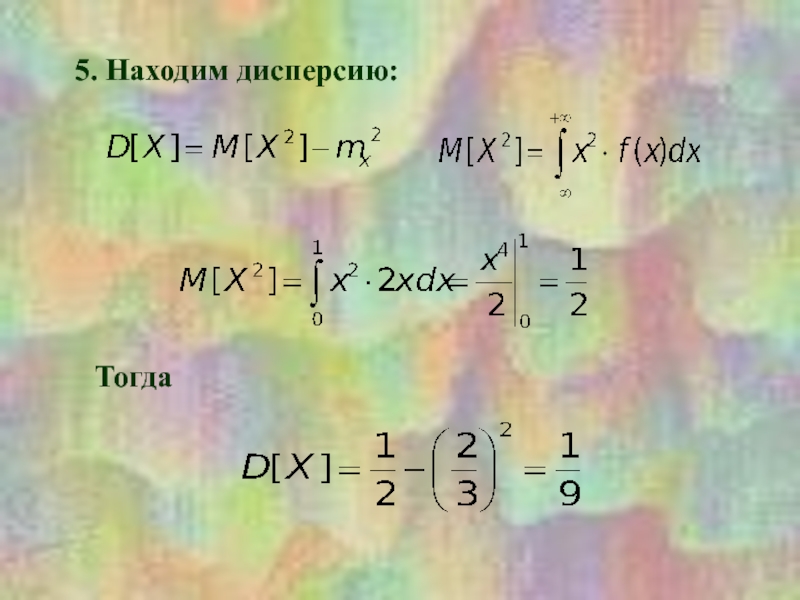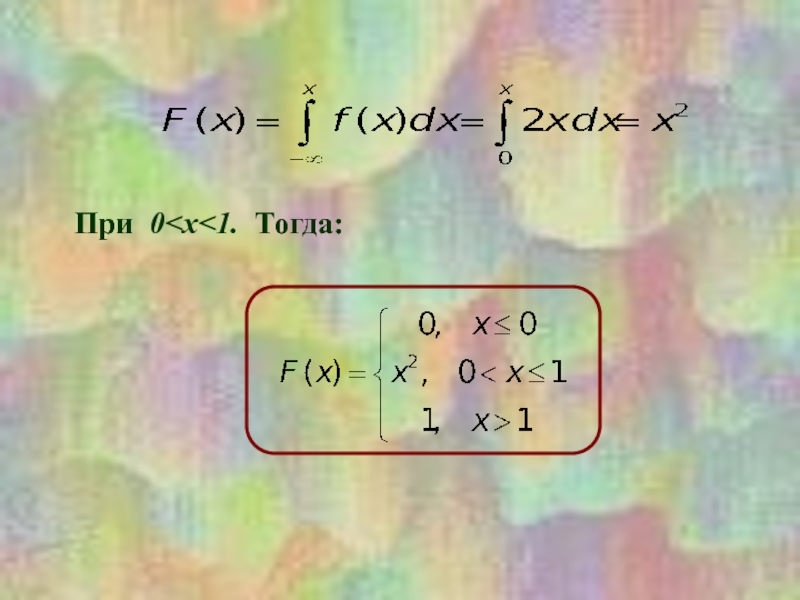TheSlide.ru

Смысл математического ожидания и дисперсии остается таким же, как и в случае

Содержание

1. Смысл математического ожидания и дисперсии остается таким же, как и в случае
2. Дискретные СВНепрерывные СВ
3. Функция распределения непрерывной случайной величины задана
4. 1. Так как функция распределения F(x) непрерывна,
5. 3. Вычисление вероятности попадания на заданный участок
6. 2 способ. Используем формулу нахождения вероятности через плотность вероятности:4. Находим математическое ожидание:
7. 5. Находим дисперсию:Тогда
8. Случайная величина Х подчиняется закону распределенияНайти величину a и функцию распределения.ПРИМЕР.
9. РЕШЕНИЕ.2. Функция распределения находится путем интегрирования плотности
10. При 0
11. Скачать презентанцию

Дискретные СВНепрерывные СВ

Главная
Разное
Смысл математического ожидания и дисперсии остается таким же, как и в случае

Слайды и текст этой презентации

Слайд 1Смысл математического ожидания и дисперсии остается таким же, как и

в случае дискретных случайных величин. Меняется вид формул для их

нахождения путем замены:

19. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
И ДИСПЕРСИЯ НЕПРЕРЫВНОЙ
СЛУЧАЙНОЙ ВЕЛИЧИНЫ

Тогда получаем формулы для расчета математического ожидания и дисперсии непрерывной случайной величины:

Смысл математического ожидания и дисперсии остается таким же, как и в случае дискретных случайных величин. Меняется вид

Слайд 2Дискретные СВ
Непрерывные СВ

Дискретные СВНепрерывные СВ

Слайд 3 Функция распределения непрерывной
случайной величины задана выражением:
Найти величину a,

плотность вероятности,
вероятность попадания на участок (0.25-0.5),
математическое ожидание и

дисперсию .

ПРИМЕР.

Функция распределения непрерывной случайной величины задана выражением:Найти величину a, плотность вероятности, вероятность попадания на участок (0.25-0.5),

Слайд 41. Так как функция распределения F(x) непрерывна, то при х=1

ax2=1, следовательно, a=1.
2. Плотность вероятности находится, как производная от функции

распределения:

РЕШЕНИЕ.

1. Так как функция распределения F(x) непрерывна, то при х=1 ax2=1, следовательно, a=1.2. Плотность вероятности находится, как

Слайд 53. Вычисление вероятности попадания на заданный участок может быть произведено

двумя способами: с помощью функции распределения и с помощью плотности

вероятности.
1 способ.
Используем формулу нахождения вероятности через функцию распределения:

3. Вычисление вероятности попадания на заданный участок может быть произведено двумя способами: с помощью функции распределения и

Слайд 62 способ.
Используем формулу нахождения вероятности через плотность вероятности:
4. Находим

математическое ожидание:

2 способ. Используем формулу нахождения вероятности через плотность вероятности:4. Находим математическое ожидание:

Слайд 75. Находим дисперсию:
Тогда

5. Находим дисперсию:Тогда

Слайд 8Случайная величина Х подчиняется
закону распределения
Найти величину a и функцию

распределения.
ПРИМЕР.

Случайная величина Х подчиняется закону распределенияНайти величину a и функцию распределения.ПРИМЕР.

Слайд 9РЕШЕНИЕ.
2. Функция распределения находится путем интегрирования плотности вероятности:
1. Для

нахождения параметра a используем свойство плотности распределения:

РЕШЕНИЕ.2. Функция распределения находится путем интегрирования плотности вероятности: 1. Для нахождения параметра a используем свойство плотности распределения:

Слайд 10При 0

При 0

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей