Software and Computing

of logical functions optimization
Simple digital devices
Technical implementation of logical devices
Assistant

professor: Poletaev Alexander

IRKUTSK NATIONAL RESEARCH TECHNICAL UNIVERSITY

principles of reasoning (thinking) concerned with relationships between given conditions

which allows us to make conclusions based on premises and assumptions.
Gottfried Leibniz suggested term «Mathematical logic» as a subfield of mathematics exploring the applications of formal logic to mathematics. But this new area did not attracted any attention of scientists. Not many people knew about mathematical logic until the middle of the XIX-th century.
Algebra of logic became an object of a great interest thanks to a self-taught English mathematician George Boole. It appeared that the logical system created by Boole can be perfectly used for mathematical formalization of switching processes in electrical circuits.

George Boole

Gottfried Leibniz

electronics, and it is provided for in all modern programming

languages. It is also used in set theory and statistics.
In algebra of logic logical statements, functions, and laws are used.
Algebra of logic (or Boolean algebra) is the branch of algebra which studies statements from a point of view of logical values and their logical operations.
A logical statement is a meaningful declarative sentence that can be either false or true. For example, the statement «Number 10 is even» is true, but the statement «Tel Aviv is the capital of Israel» is false.
Questions or imperatives do not make statements: "Who are you?", "Run!". As well as sentences of opinion or taste: “She wears a nice dress", "Broccoli is delicious".

George Boole

Gottfried Leibniz

(simple) or compound (a combination of
several simple statements).
Compound

expressions include two or more simple statements which are connected via logical connectives (operations). For example, the compound expression

«Number 10 can be divided by 2 and it cannot be divided by 5»

consists of two simple statements («Number 10 can be divided by 2» which is true, «Number 10 cannot be divided by 5» which is false), and there is the logical connective «AND» between them. So, logically the whole expression is false. But the statement «Number 10 can be divided by 2 and it cannot be divided by 3» is true.

or false depending on the combination of logical values of

simple statements.

In order to address to logical statements they are assigned to be logical variables (A, B, x, y, ….), i.e. each simple statement is considered to be a variable with assigned name.
If logical variable is true then its value is logical 1, otherwise it has logical 0 value. Each logical connective is considered to be a logical operations and has a unique name and notation. Logical operations are also characterized by the truth table describing the result for all possible combinations of logical variable values.
In digital devices logical operations are executed in logical gates (elementary electronic circuit).

the ANSI ('American'), and the IEC ('European', or also Russian

'GOST')

& B
Rule: the statement А & В is true only

when А and В are both true.
# Example. «Number 10 can be divided by 2 and it cannot be divided by 5» is conjunction where A = «Number 10 can be divided by 2 » и B = «Number 10 cannot be divided by 5». The first one is true but the second one is false. Thus, the whole expression is false in general (check via the Venn diagram).



AND logic gate

Truth Table

IEC

ANSI

∧

Diode AND gate:

Logic gate notation:

A

Venn diagram of A ∧ B

A+B
Rule: the expression А ∨ В is false when simple

statements А and В are both false. If even one of them is true then their disjunction is also true.
# Example. The expression «An application for the scholarship can be done via electronic copies or this can be done using hard copies» is true as you can apply for the scholarship using any of these forms of application.


OR logic gate

Truth Table

IEC

ANSI

OR

OR

Diode OR gate

Venn diagram of A ∨ B

А→В is false only when А is true and В

is false.
# Example 1. «If a student gets ‘good’ and ‘excellent’ marks for exams he will get scholarship».
The expression is false only when a student passes exams without bad mark scholarship is not given. For other cases it is true. Even when a student gets bad marks it is possible to have a social scholarship (or some other ones).
# Example 2. «If it is raining then the asphalt at the streets is wet». When it is raining (true) but the asphalt is somehow dry (false) the whole situation becomes false.
# Example 3. «When it is rainy people carry umbrellas». In general you will see a lot of people with umbrellas during rainy days. But what if it is shiny? It covers from sun.
IMPLY gate

Truth table

IEC

ANSI

Note. Do not mix up the implication (→) and the logical consequence (⇒). The logical consequence A ⇒ B means that in all cases when A is true, B is consequently true.

Venn diagram of А→В

!

В , А XOR В
Rule: the expression А ⊕

В is true only when the values of A and B do not coincide.
# Example. The expression «This summer I am going either to Prague or to Paris» means that I am going to visit Prague or Paris but not both capitals (case when both statements are true). But at the same time it is not reasonable to stay at home because I have already spent money and time on the necessary paperwork (getting passport, Schengen Visa, vacation arrangements at work and so on).
The XOR operation is commonly used in cryptography, error-correcting encoding, in many digital devices, in telecommunication systems, computer networks for data integrity checking, etc.)
XOR gate

Truth Table

IEC

ANSI

Note. XOR is also can be treated as modular arithmetic operation. Modular arithmetic is related to finding remaining of a division like 10 mod 4 ≡ 2.

For the binary operation XOR it is respective to
А ⊕ В = (A + B) mod 2

!

Venn diagram of А ⊕ В

~ B
Rule: a statement A↔B is true if and only

if values of A and И coincide.
# Example 1. «The triangle is rectangular if and only if it has 90 degrees angle». This compound expression is true only for two cases: 1) when we claim that the triangle is rectangular (1) and one of its angles is 90 degrees (1); 2) The triangle is not rectangular (0) is not right and it has no right angles (0).
# Example 2. «Two lines are parallel if they are not crossed». Try to do here the same reasoning.
XNOR gate

Truth Table

IEC

ANSI

Venn diagram of А ↔ В

metal–oxide–semiconductor field-effect transistor
Venn diagram of A ↓ B
IEC
ANSI

NAND gate (diode-transistor logics):
NAND cells in flash memory devices (SSD,

USB Flash drive)

MOSFET
transistors

If one of the transistors is closed the bit line is at high voltage level state (“1”)

(…);
Negation ¬;
Conjunction &;
Disjunction ∨, Exclusive OR ⊕;
Implication →;
Equivalence ↔.

Node
Crossing of

wires

This circuit can be replaced with the single logic gate →

the same result for the same input values then they

are considered to be equal.
Logic optimization is the process of finding an equivalent representation of the specified logic circuit under one or more specified constraints (limits). Generally the circuit is constrained to minimum chip area meeting a prespecified delay.
Optimization gives lots of advantages:
Logical circuits become smaller. Each chip can contain more logical devices;
The less logic gates are used the less if total delay. Optimization increases response speed so the device works faster.
The device with less number of logical gates is more reliable. Minimization decreases possibility of breakdown of one of them.
The optimized logical circuits are cheaper.
There are different ways for optimization:
Method of equivalent transforms (Boolean algebra laws);
Veitch charts method;
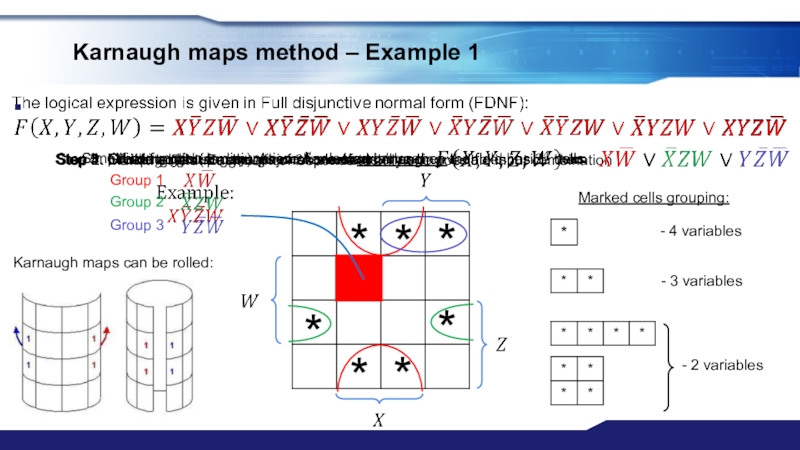
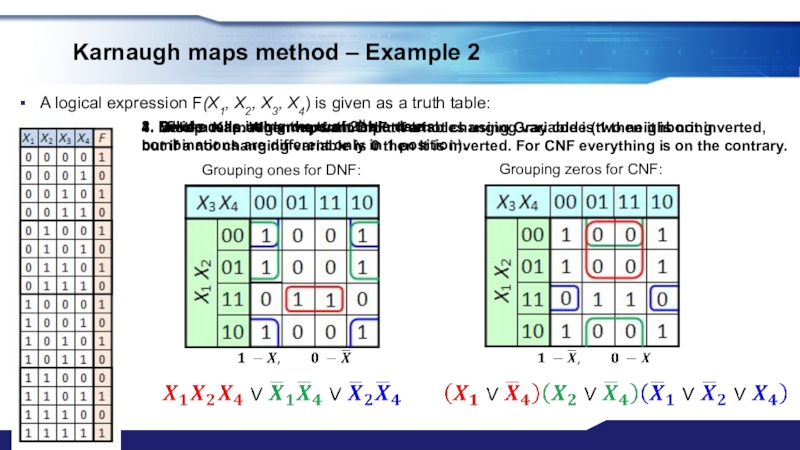
Method of Karnaugh maps;
Quine algorithm;
Quine – McCluskey algorithm.

Pulse delay in logical gates

Commutativity (commutative laws):
– for disjunction: A ∨ B = B

∨ A;
– for conjunction: A ∧ B = B ∧ A;
3) Associativity (associative laws):
– for disjunction: (A ∨ B) ∨ C = A ∨ (B ∨ C);
– for conjunction: (A ∧ B) ∧ C = A ∧ (B ∧ C);
4) Distributivity (Distributive laws):
– for disjunction: (A ∨ B) & C = (A & C) ∨ (B & C);
– for conjunction: (A & B) ∨ C = (A ∨ C) & (B ∨ C);
5) De Morgan's laws:
– for disjunction: ¬ (A ∨ B) = ¬A & ¬B;
– for conjunction: ¬ (A & B) = ¬A ∨ ¬B;
6) Idempotence laws:
– for disjunction: A ∨ A = A;
– for conjunction: A ∧ A = A;

7) Identity laws:
– for disjunction: A ∨ 0 = A;
– for conjunction: A ∧ 1= A;
8) Annihilation laws
– for disjunction: A ∨ 1 = 1;
– for conjunction: A ∧ 0= 0;
9) Complementation laws:
– for disjunction: A ∨ ¬A = 1;
– for conjunction: A & ¬A= 0;
10) Absorption laws:
– for disjunction: A ∨ (A & B) = A;
– for conjunction: A & (A ∨ B) = A;
11) Elimination rule for implication:
A → B = ¬A ∨ B;
12) Elimination rule for equivalence :
A ↔ B = (A → B) ∧ (B → A).

& ¬A) ∨ (A & ¬B).
1. According to the De

Morgan’s law:
¬ (B & ¬A) ∨ (A & ¬B) = ¬B ∨ ¬(¬A) ∨ (A & ¬B).
2. Using the double negation law we can rewrite it as:
¬B ∨ ¬(¬A) ∨ (A & ¬B) = ¬B ∨ A ∨ (A & ¬B).
3. According to commutative and absorption laws:
¬B ∨ A ∨ (A & ¬B) = A ∨ ¬B ∨ (A & ¬B) = A ∨ ¬B.
4. Elimination rule for implication:
A ∨ ¬B = B → A.
Finally, we proved that the given expression can be replaced with implication:
¬ (B & ¬A) ∨ (A & ¬B) = B → A.

# Task. Optimize the logical function ¬ (A ∨ B) ∧ (A & ¬B).

field. Each cell corresponds to only one possible input combination
Step

3. Fill the table using the given expression items

Step 5. Grouping: groups are conjunctions of not changing variables inside them

Karnaugh maps method – Example 1

*

*

*

*

*

*

*

Karnaugh maps can be rolled:

- 4 variables

- 3 variables

- 2 variables

Marked cells grouping:

Group 1

Group 2

Group 3

Karnaugh map from input variables using Gray code (two neighboring

combinations are different only in 1 position).

4. Group cells. When we want DNF: if a not changing variable is 1 then it is not inverted, but if a not changing variable is 0 then it is inverted. For CNF everything is on the contrary.

2. Fill the map using the truth table data

Karnaugh maps method – Example 2

A logical expression F(X1, X2, X3, X4) is given as a truth table:

Grouping ones for DNF:

Grouping zeros for CNF:

memory cells (a latch, a flip-flop)
Asynchronous latches switch their states

immediately at the moment of their input signal changes.
SR latch is a digital device with separate (independent) setting of logical 1 and logical 0 states. It has two information inputs: S (set) and R (reset). 
1 at the S input switches SR latch to Q = 1 state, 1 at the R input switches to Q = 0 state.

1

0

0

1

0

0

0

0

1

D means an input for information (data input), and the

С inputs is for clock pulses (synchronization input).
1 at the C input makes recording data from the D input.
When there is 0 at the C input the latch keeps the previous state (data storing mode).
D latch is a circuit which delays input pulses for a one clock cycle.

transistors latch (flip-flop)

a chip with the logical gate NOR with 3 inputs

that the inner structure of the PLD integrated circuit can

be changed programmatically. It implements logical operations at the hardware level. Some types of PLD are programmed only for one time, some of them enable multiple reconfiguration.

a so-called Macrocell matrix which contain a certain set of

logical gates and devices (D latches, multiplexers, AND gates, OR gates, inverters, etc.).
Macrocell blocks are connected via programmable cross-point arrays.

CPLD general structure:

Logic array