Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сопромат+литература
Содержание
- 1. Сопромат+литература
- 2. Сопротивление материалов – наука о прочности
- 3. Литература1. Ицкович Г.М. Сопротивление материалов. 2. Феодосьев
- 4. Задачи сопротивления материаловПервая задача - расчет элементов
- 5. Задачи сопротивления материаловВторая задача - расчет элементов
- 6. Задачи сопротивления материаловТретья задача - расчет элементов конструкций на устойчивость
- 7. Классификация силВнешние силы: активные (нагрузки) и реактивные
- 8. Классификация силПо характеру изменения во времени различают:
- 9. Связи и их реакции Опора шарнирно-подвижная -
- 10. Связи и их реакцииОпора шарнирно неподвижная (цилиндрический шарнир)
- 11. Опора защемляющая (жесткая заделка, консоль)
- 12. Формы элементов конструкций:Брус - тело, два измерения
- 13. Примеры брусьев различной формы
- 14. Формы элементов конструкций:Оболочка (пластина) - тело, одно измерение которого мало по сравнению с двумя другими
- 15. Массив тело, все три измерения которого -
- 16. ГИПОТЕЗЫ И ДОПУЩЕНИЯ,ПРИНЯТЫЕ В СОПРОТИВЛЕНИИ МАТЕРИАЛОВ
- 17. Материал однороден, т. е. свойства любых
- 18. 2. Тело рассматривается как сплошная
- 19. Материал изотропен, т.е. физико-механические свойства его по
- 20. В известных пределах нагружения материал обладает идеальной упругостью, т.е. после снятия нагрузки деформации полностью исчезают
- 21. 5. Перемещения точек упругого тела в известных
- 22. Роберт Гук 1635–1703
- 23. 6. Гипотеза Бернулли о плоских сечениях –
- 24. 7. Принцип Сен-Венана – в сечениях, достаточно
- 25. Адемар Жан-Клод Барре де СЕН-ВЕНАН(1797 - 1886)
- 26. Слайд 26
- 27. 8. Принцип независимости действия сил (принцип
- 28. 9. Принцип начальных размеров (гипотеза о малости
- 29. Внутренние силовые факторы
- 30. Метод сечений - определение внутренних усилий путем составления уравнений равновесия любой отсеченной части тела
- 31. Слайд 31
- 32. Слайд 32
- 33. Слайд 33
- 34. Слайд 34
- 35. Внутренние силовые факторы – проекции главного вектора
- 36. Напряжения Напряжение механическое полное – мера интенсивности
- 37. Огюстен Луи Коши 1789 - 1857
- 38. Слайд 38
- 39. Слайд 39
- 40. Растяжение (сжатие) – вид деформации, при котором
- 41. РАСТЯЖЕНИЕ возникает, если противоположно направленные силы приложены
- 42. Напряжения в поперечных сечениях брусаПри
- 43. Деформации при растяжении и сжатии Закон Гука
- 44. Современное определение модуля Юнга было дано в 1826
- 45. Томас Юнг (Янг)(1773-1829) английский физик, механик, врач, астроном и востоковед, один из создателей волновой теории света
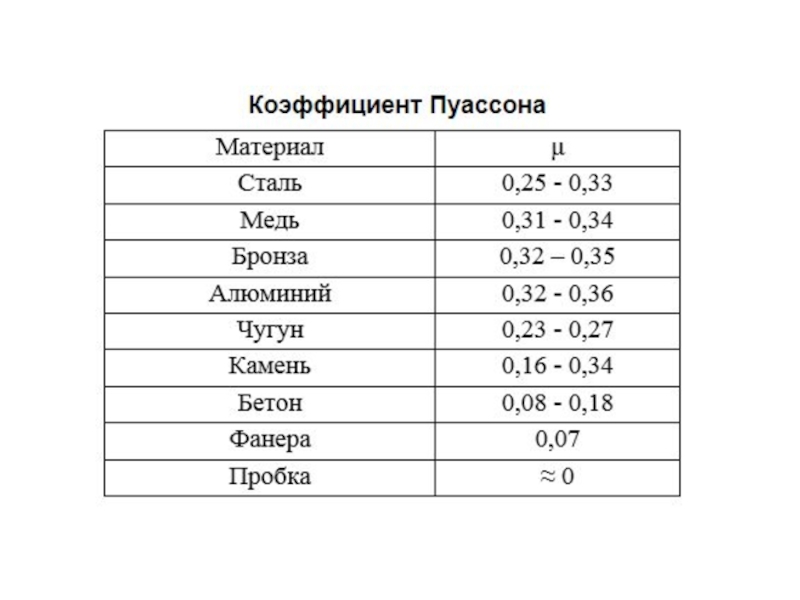
- 46. Коэффициент Пуассона
- 47. Симеон Дени ПУАССОН(1781-1840)
- 48. Как показывает опыт, при растяжении бруска длина
- 49. Слайд 49
- 50. Слайд 50
- 51. Слайд 51
- 52. Деформации стержня при растяжении-сжатии
- 53. Слайд 53
- 54. Слайд 54
- 55. Слайд 55
- 56. Энергия деформации при растяжении
- 57. Теорема Клапейрона«Работа силы, статически приложенной к линейно-деформируемой
- 58. Суммируя по всей длине стержня, определяемДля всей системы
- 59. Для стержня (участка стержня) постоянного поперечного сечения
- 60. Бенуа Поль ЭмильКЛАПЕЙРОН(1799-1864)
- 61. Механические испытания материалов Стандартные образцы для испытаний
- 62. Учебная испытательная машина МИ-40КУ:1 – станина; 2
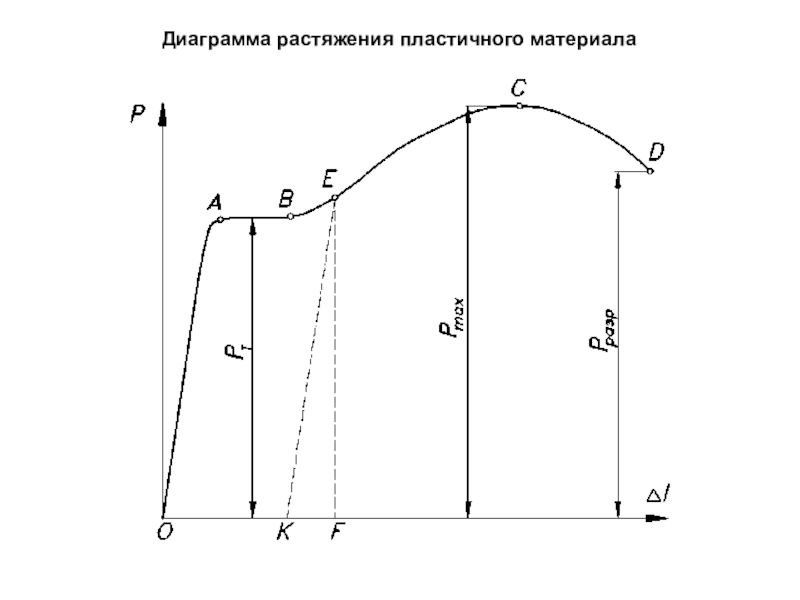
- 63. Диаграмма растяжения пластичного материала
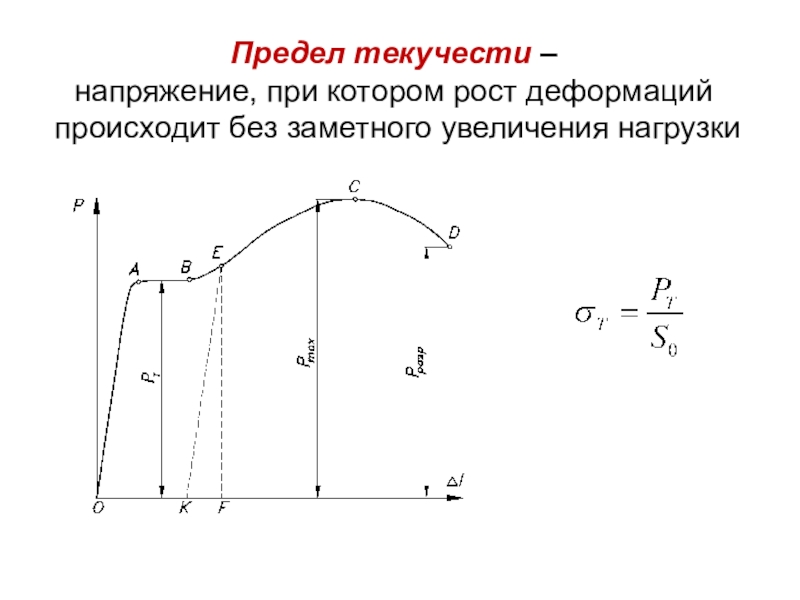
- 64. Предел текучести – напряжение, при котором рост деформаций происходит без заметного увеличения нагрузки
- 65. Временное сопротивление в или предел прочности материала
- 66. Истинное напряжениев момент разрыва (в точке D):
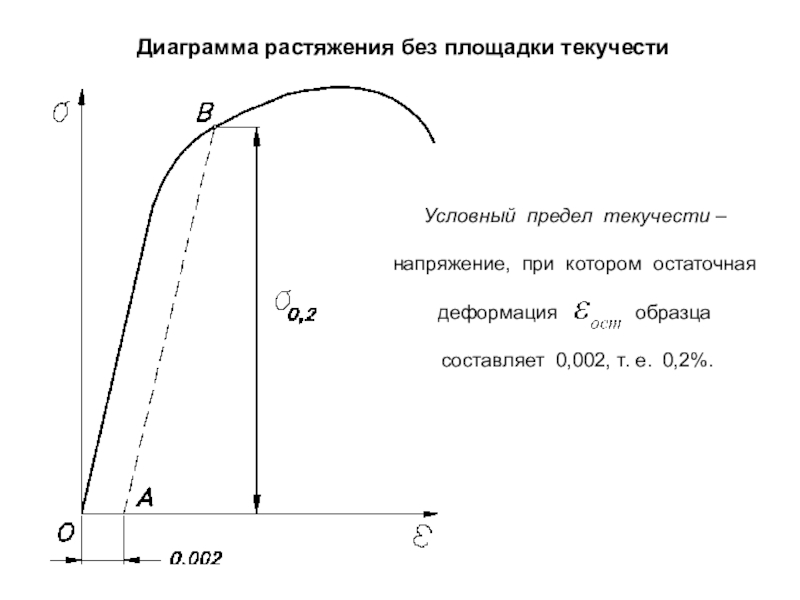
- 67. Диаграмма растяжения без площадки текучести Условный предел
- 68. Скачать презентанцию
Сопротивление материалов – наука о прочности и деформируемости элементов (деталей) сооружений и машин
Слайды и текст этой презентации
Слайд 2Сопротивление материалов – наука о прочности и деформируемости элементов (деталей)
сооружений
и
машин
Слайд 3Литература
1. Ицкович Г.М. Сопротивление материалов.
2. Феодосьев В.И. Сопротивление материалов.
3. Петрухин Г.Г. Сопротивление материалов. Контрольные задания. Руководство к
решению задач. - Новогорск: АГЗ, 1998. 4. Закатов М.М., Курбатский М.И., Монтвила С.П. Руководство к лабораторным работам по дисциплине «Механика». Часть I. – Химки: АГЗ МЧС России, 2009, 68 с.
5. Курбатский М.И. Механика. Энциклопедический словарь. Часть I. Теоретическая механика и сопротивление материалов. Учебное пособие
Слайд 4Задачи сопротивления материалов
Первая задача - расчет элементов конструкций на прочность.
Прочность
- способность детали
сопротивляться разрушению или возникновению пластических деформаций под действием
приложенных к ней нагрузокСлайд 5Задачи сопротивления материалов
Вторая задача - расчет элементов конструкций на жесткость
Жесткость
- способность материала или элемента конструкции воспринимать нагрузку
без существенного изменения геометрических размеровСлайд 7Классификация сил
Внешние силы: активные (нагрузки) и реактивные (реакции связей).
Объемные силы
– силы, действующие на каждый бесконечно малый элемент объема. К
ним относятся силы тяжести и силы инерции, возникающие при ускоренном движении.Поверхностные силы - нагрузки, передающиеся от одних элементов конструкции к другим.
Делятся на сосредоточенные и распределенные.
Нагрузки, распределенные по некоторой поверхности, характеризуются давлением, т. е. отношением силы, действующей на элемент поверхности нормально к ней, к площади данного элемента. Выражаются в паскалях.
Распределенная по длине нагрузка характеризуется интенсивностью, обозначаемой обычно q. Выражается в единицах силы, отнесенных к единицам длины: Н/м.
Слайд 8Классификация сил
По характеру изменения во времени различают:
- статические нагрузки,
нарастающие медленно и плавно от нуля до своего конечного значения;
-
повторные нагрузки, многократно изменяющиеся во времени по тому или иному закону;- нагрузки малой продолжительности, прикладываемые к конструкции сразу или даже с начальной скоростью в момент контакта (динамические или ударные).
Слайд 9Связи и их реакции
Опора шарнирно-подвижная - опора, позволяющая точке
тела, которая связана с опорой, перемещаться без трения вдоль какой-либо
поверхности. Реакция подвижной опоры направляется по нормали к поверхности, вдоль которой может перемещаться опора.Слайд 12Формы элементов конструкций:
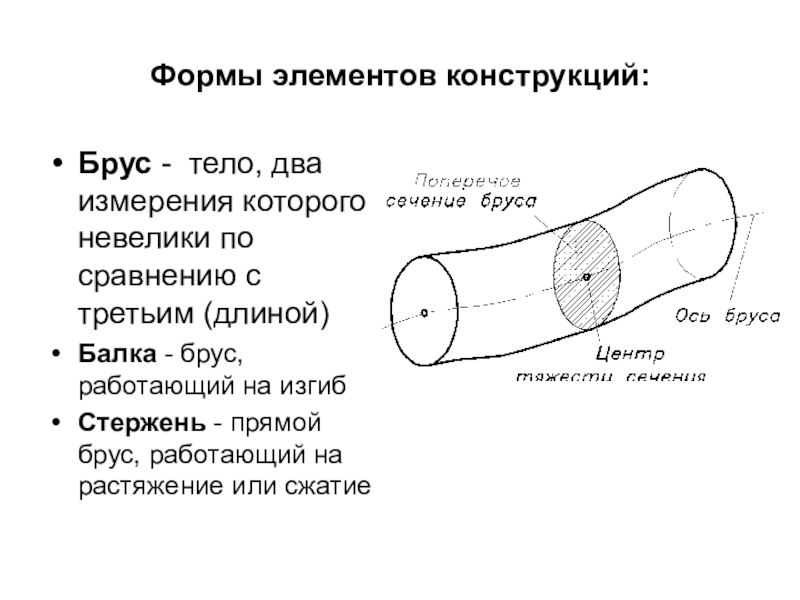
Брус - тело, два измерения которого невелики по
сравнению с третьим (длиной)
Балка - брус, работающий на изгиб
Стержень - прямой брус, работающий на растяжение или сжатие
Слайд 14Формы элементов конструкций:
Оболочка (пластина) - тело, одно измерение которого мало
по сравнению с двумя другими
Слайд 15Массив
тело, все три измерения которого - величины одного порядка
(строительный блок, шарик или ролик подшипника качения и т.д.)
Слайд 17Материал однороден,
т. е. свойства любых сколь угодно
малых его частиц совершенно тождественны.
Это допущение достаточно обосновано для
металлокристаллических материалов, например, для стали,и менее обосновано
для материалов
типа чугуна
Слайд 182. Тело рассматривается как сплошная среда,
т.е. материал
полностью заполняет весь объем тела без каких-либо пустот.
Представление
о теле как о сплошной среде дает возможность применять
методы анализа бесконечно малых величин
(дифференциальное и интегральное исчисления)
Слайд 19Материал изотропен,
т.е. физико-механические свойства его по всем направлениям одинаковы.
Материалы, не обладающие указанным свойством, называют анизотропными.
Слайд 20
В известных пределах нагружения материал обладает идеальной упругостью,
т.е. после
снятия нагрузки деформации полностью исчезают
Слайд 215. Перемещения точек упругого тела
в известных пределах нагружения
прямо
пропорциональны силам, вызывающим эти перемещения.
«Ut tensio, sic vis» -
«какова деформация, такова сила» Роберт Гук
Слайд 236. Гипотеза Бернулли о плоских сечениях –
поперечные сечения,
плоские и
нормальные к оси стержня
до приложения к нему нагрузки,
остаются
плоскими и нормальными к его оси в деформированном состоянии;при изгибе сечения поворачиваются, не искривляясь
Слайд 247. Принцип Сен-Венана –
в сечениях, достаточно удаленных от
мест приложения
нагрузки,
деформация тела
не зависит
от конкретного способа нагружения
и
определяется только статическим эквивалентом нагрузки
Слайд 27 8. Принцип независимости действия сил
(принцип суперпозиции)-
результат воздействия нескольких внешних
факторов
равен сумме результатов воздействия каждого из них, прикладываемого в
отдельности,и не зависит от последовательности их приложения
Слайд 289. Принцип начальных размеров (гипотеза о малости деформаций) –
деформации
в точках тела настолько малы по сравнению с размерами деформируемого
тела, что не оказывают существенного влияния навзаимное расположение нагрузок, приложенных к телу.
Допущение применяют при составлении
уравнений статики,
считая тело абсолютно твердым
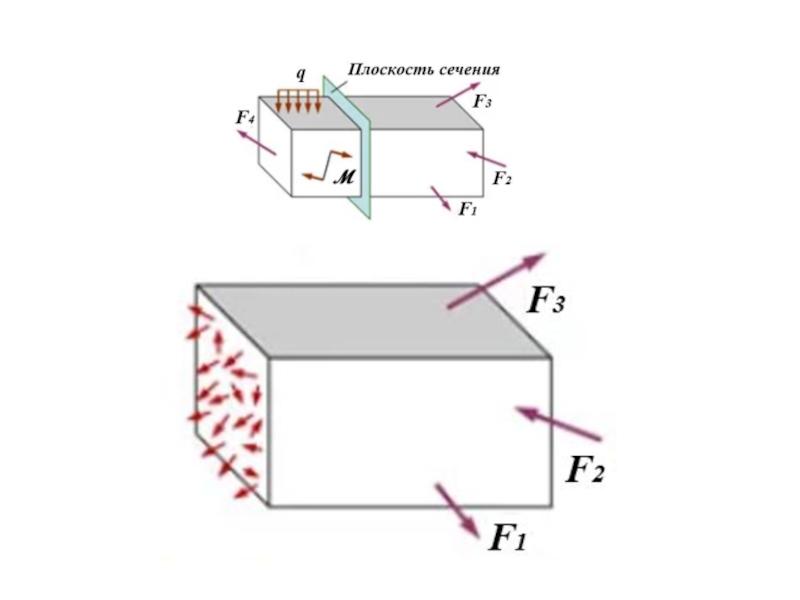
Слайд 30Метод сечений - определение внутренних усилий путем составления уравнений равновесия
любой отсеченной части тела
Слайд 35Внутренние силовые факторы – проекции главного вектора и главного момента
внутренних сил на оси координат, привязанные к центру тяжести сечения
Слайд 36Напряжения
Напряжение механическое полное – мера интенсивности распределения внутренних сил.
Для любой точки А упругого тела равно:
Слайд 40Растяжение (сжатие) –
вид деформации, при котором из шести внутренних
силовых факторов не равно нулю одно – продольное усилие N
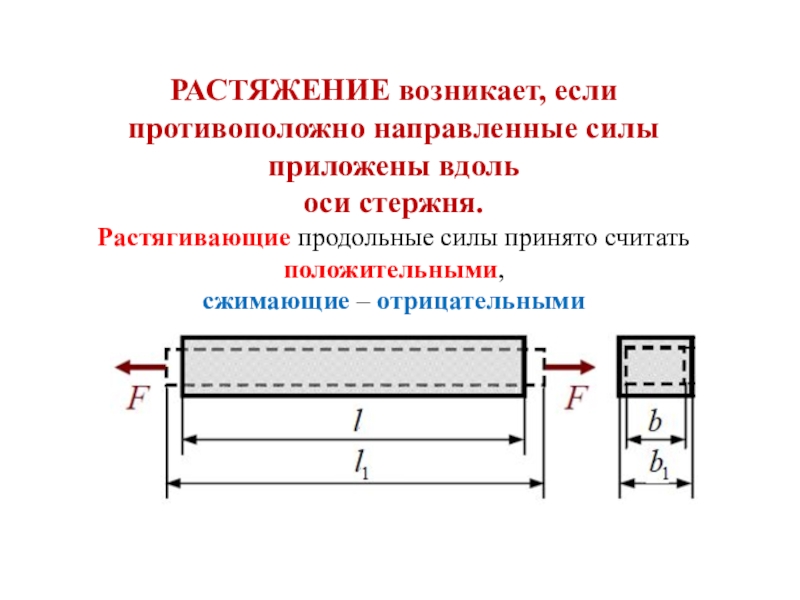
Слайд 41РАСТЯЖЕНИЕ возникает, если противоположно направленные силы приложены вдоль
оси стержня.
Растягивающие
продольные силы принято считать положительными,
сжимающие – отрицательными
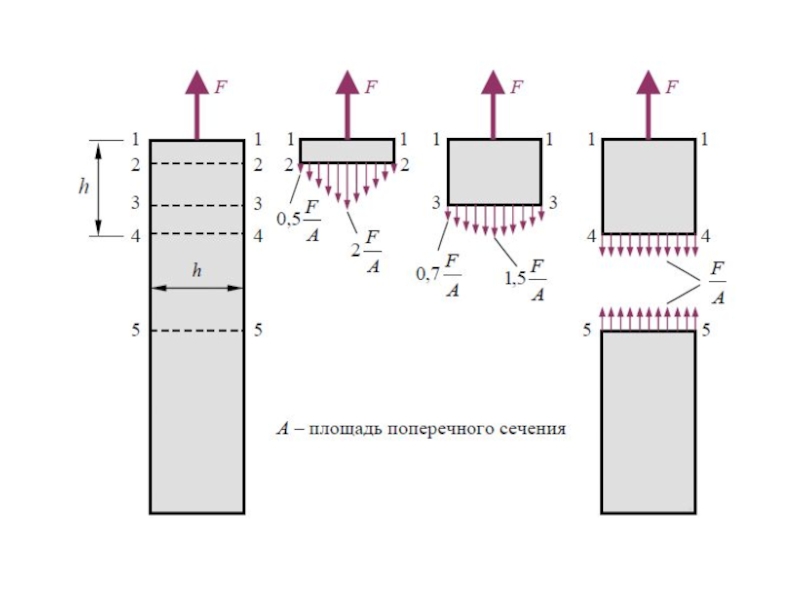
Слайд 42Напряжения в поперечных сечениях бруса
При растяжении (сжатии) бруса
в его поперечных сечениях возникают только нормальные напряжения.
Равнодействующая соответствующих
элементарных сил - продольная сила N - может быть найдена с помощью метода сечений. Для того чтоб иметь возможность определить нормальные напряжения при известном значении продольной силы, необходимо установить закон их распределения по поперечному сечению бруса.
Эта задача решается на основе гипотезы плоских сечений (гипотезы Я. Бернулли), которая гласит: сечения бруса, плоские и нормальные к его оси до деформации, остаются плоскими и нормальными к оси и при деформации.
Слайд 44Современное определение модуля Юнга
было дано в 1826 г.
за три
года до смерти Юнга
французским инженером Навье
Слайд 45Томас Юнг (Янг)
(1773-1829)
английский физик,
механик, врач,
астроном и востоковед, один из создателей волновой теории света
Слайд 48Как показывает опыт, при растяжении бруска длина его увеличивается на
величину Δl, ширина же уменьшается на величину
Относительная продольная
деформация равна относительная поперечная деформация равна
Слайд 57Теорема Клапейрона
«Работа силы, статически приложенной к линейно-деформируемой системе, равна половине
произведения конечного значения силы на конечное значение соответствующего перемещения»
Слайд 59Для стержня (участка стержня)
постоянного поперечного сечения
при условии,
что
продольная сила по длине стержня
не изменяется:
Слайд 61Механические испытания материалов
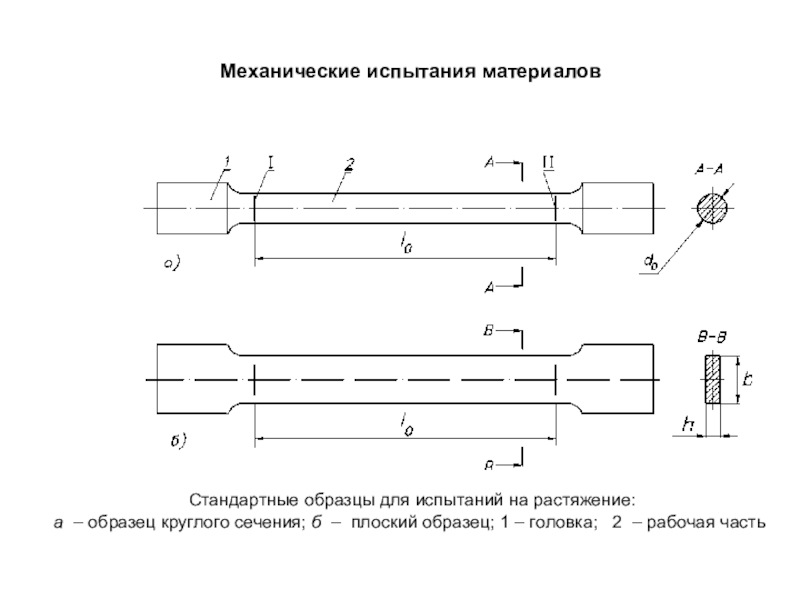
Стандартные образцы для испытаний на растяжение:
а –
образец круглого сечения; б – плоский образец; 1 – головка;
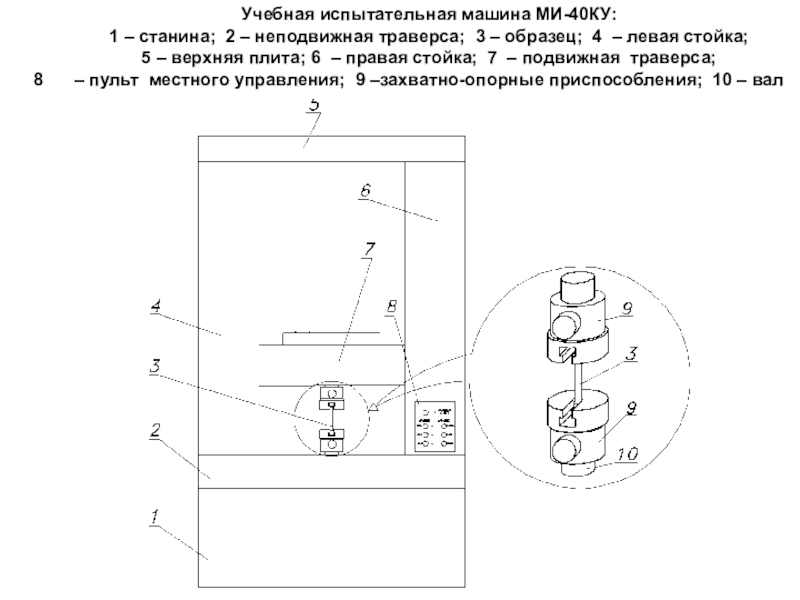
2 – рабочая частьСлайд 62Учебная испытательная машина МИ-40КУ:
1 – станина; 2 – неподвижная траверса;
3 – образец; 4 – левая стойка;
5 – верхняя
плита; 6 – правая стойка; 7 – подвижная траверса; – пульт местного управления; 9 –захватно-опорные приспособления; 10 – вал
Слайд 64Предел текучести –
напряжение, при котором рост деформаций
происходит без
заметного увеличения нагрузки
Слайд 65Временное сопротивление в
или предел прочности материала –
отношение максимальной
силы, которую способен выдержать образец,
к его начальной площади поперечного
сечения Слайд 67Диаграмма растяжения без площадки текучести
Условный предел текучести –
напряжение,
при котором остаточная
деформация
образца составляет 0,002, т. е. 0,2%.