Слайд 1Составляющие сопротивления
движению судов
Слайд 3Далее рассматриваем только однокорпусные
водоизмещающие суда в режиме плавания…
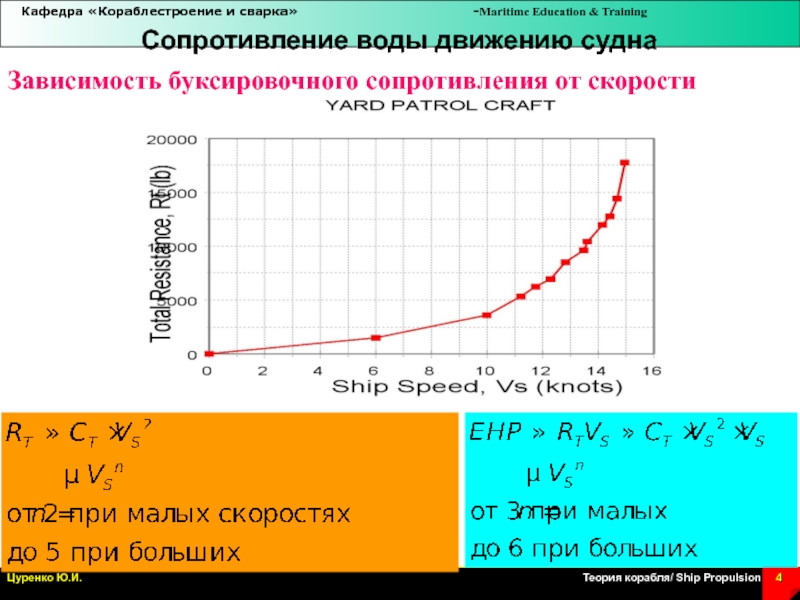
Слайд 4Зависимость буксировочного сопротивления от скорости
Сопротивление воды движению судна
Слайд 5Буксировочное сопротивление, обозначаемое R, размерная величина
RT = Буксировочное сопротивление есть
сумма составляющих
RT = RAA + RW + RV
RAA = Сопротивление
надводной части корпуса, надстроек и т.п.
RW = Волновое сопротивление (потери на волнообразование)
- функция отношения длины к ширине, водоизмещения, формы обводов, числа Фруда (соотношения длины и скорости)
RV = Вязкостное сопротивление (сопротивление сил трения в воде)
- Функция вязкости воды, скорости, площади и формы смоченной поверхности
Вязкостное сопротивление
Волновое сопротивление
Сопротивление воздуха
(Данное деление принято для водоизмещающих судов на тихой воде)
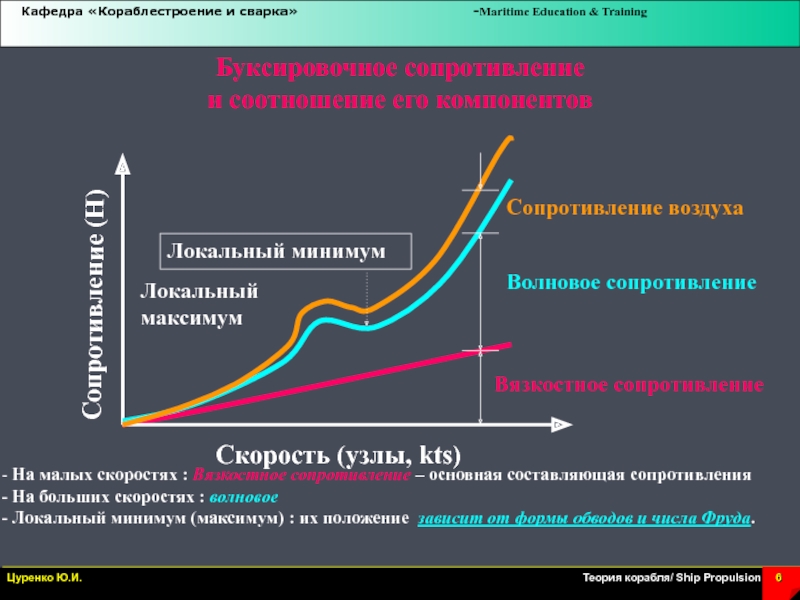
Слайд 6Буксировочное сопротивление
и соотношение его компонентов
Вязкостное сопротивление
Сопротивление воздуха
Волновое сопротивление
Скорость (узлы,
kts)
Сопротивление (Н)
На малых скоростях : Вязкостное сопротивление – основная
составляющая сопротивления
На больших скоростях : волновое
Локальный минимум (максимум) : их положение зависит от формы обводов и числа Фруда.
Локальный
максимум
Локальный минимум
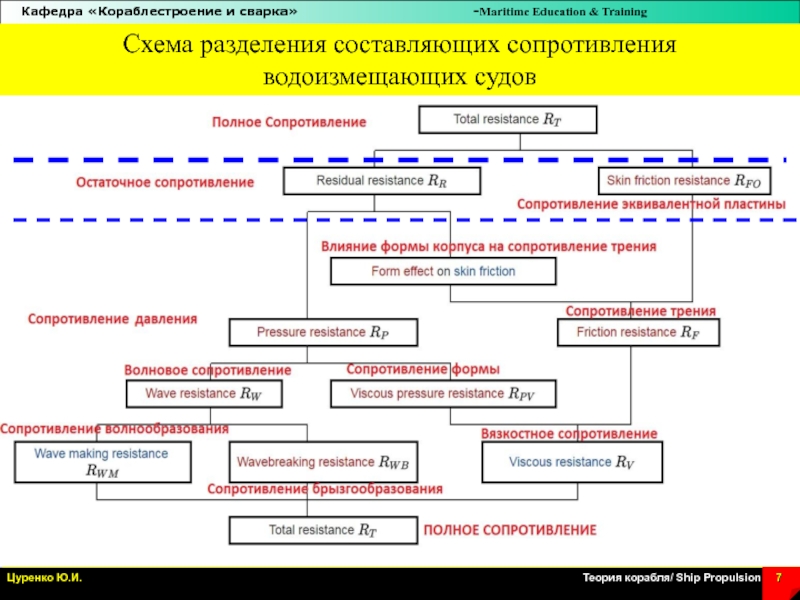
Слайд 7Схема разделения составляющих сопротивления
водоизмещающих судов
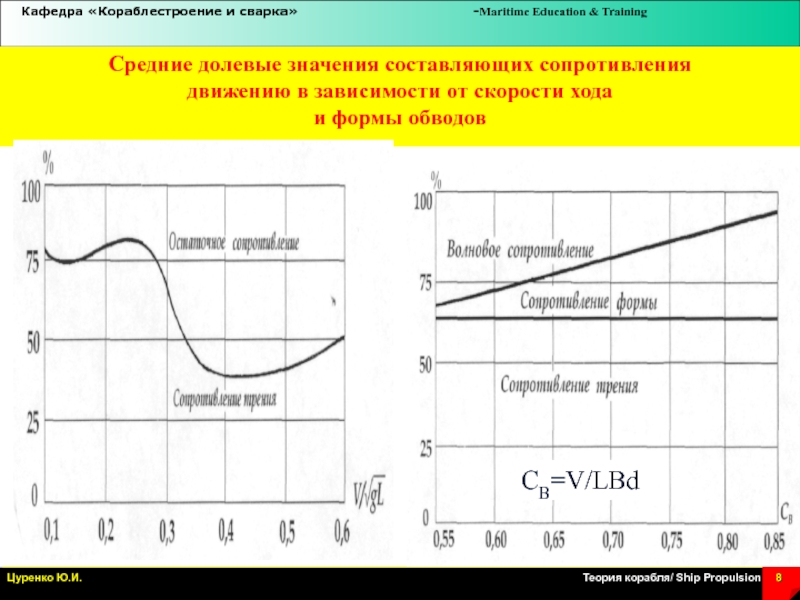
Слайд 8Средние долевые значения составляющих сопротивления
движению в зависимости от скорости хода
и
формы обводов
CB=V/LBd
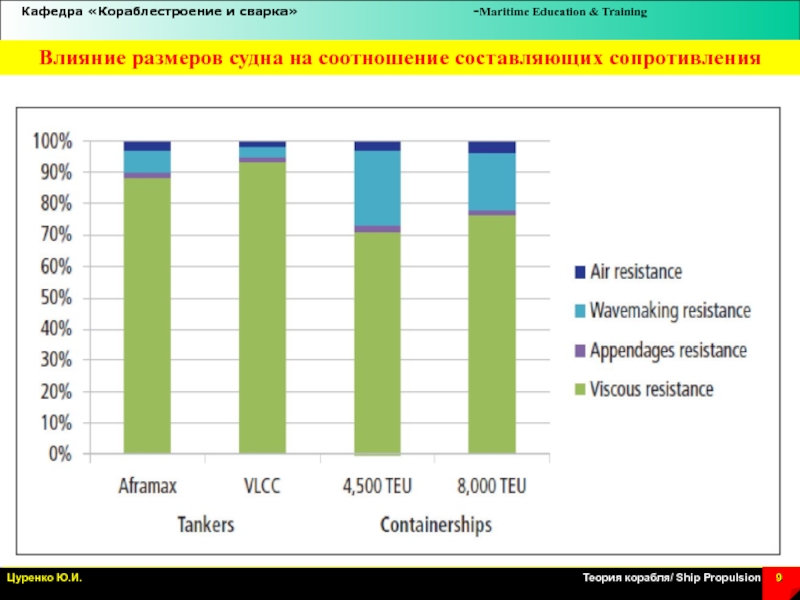
Слайд 9Влияние размеров судна на соотношение составляющих сопротивления
Слайд 111871 год – Вильям Фруд (Торквей, Англия) построил первый бассейн с
тележкой, а в 1873 году он разработал метод пересчёта сопротивления с модели
на натуру, пользуясь законом гравитационного подобия, идея которого принадлежит Реху (1844).
Фруд впервые предложил научный метод пересчёта на натуру результатов измерений, полученных на моделях в бассейне. Метод Фруда является одним из самых замечательных по своей практичности. Для выделения сопротивления трения Фруд высказал идею об эквивалентных досках. Проводятся буксировочные испытания тонких досок, площадь которых равна площади смоченной поверхности корпуса судна, а потом их сопротивление вычитается из полного сопротивления судна. Таким путём получается остаточное сопротивление, которое пересчитывается на натуру по закону подобия Фруда. Кроме того, Фруд получил критерий подобия гравитационных сил модели и судна, который называется числом Фруда. Экспериментальная теория Фруда до сих пор сохраняет своё преимущественное значение, потому что приближения теории всё ещё менее точны, чем эксперименты.
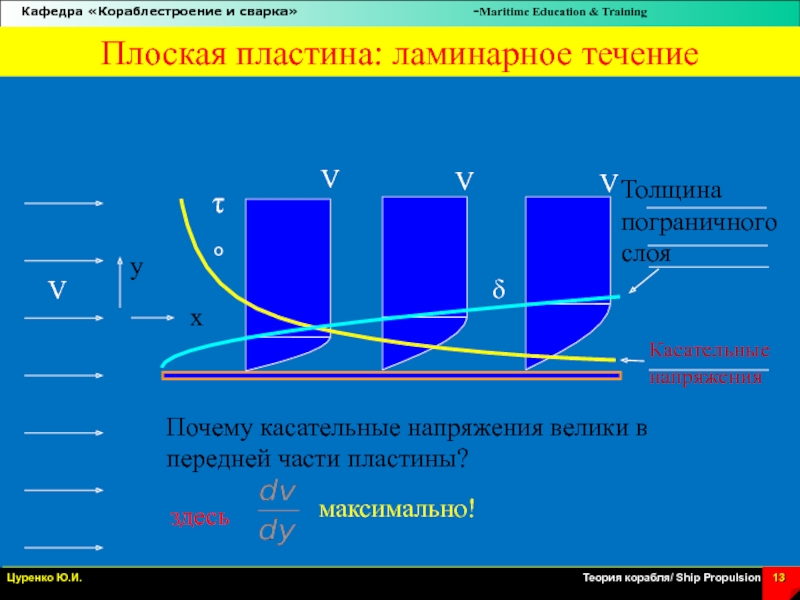
Слайд 13Плоская пластина: ламинарное течение
x
y
d
Почему касательные напряжения велики в передней части
пластины?
Толщина пограничного слоя
Касательные напряжения
максимально!
to
здесь
Слайд 14Плоская пластина (ламинарное течение):
касательные напряжения и сила трения
Толщина пограничного слоя
прямо пропорциональна корню квадратному oт расстояния до входящей кромки!
По одной
стороне пластины!
Предполагаем подобие безразмерных эпюр скоростей в пограничном слое
Интегрируем вдоль пластины
Слайд 15Плоская пластина (ламинарное течение):
коэффициент силы трения
Анализ зависимости
Слайд 16Переход ламинарного пограничного слоя в турбулентный
Пограничный слой становится турбулентным при
числах Рейнольдса порядка 500,000 (Х по длине пластины)
В этом месте
пластины толщина пограничного слоя
становится критически большой!
Red = 3500
=
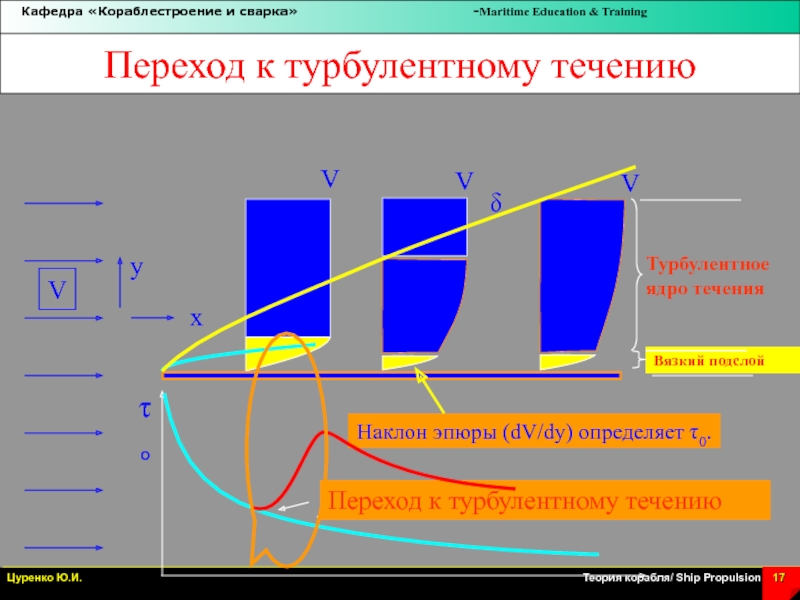
Слайд 17Переход к турбулентному течению
x
y
V
d
to
V
Турбулентное
ядро течения
Вязкий подслой
Наклон эпюры (dV/dy) определяет
t0.
Переход к турбулентному течению
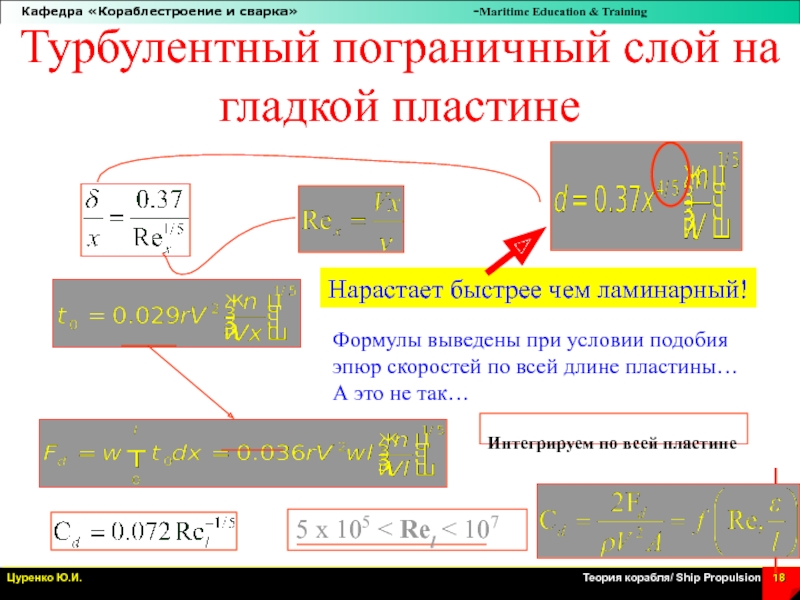
Слайд 18Турбулентный пограничный слой на гладкой пластине
Интегрируем по всей пластине
5 x
105 < Rel < 107
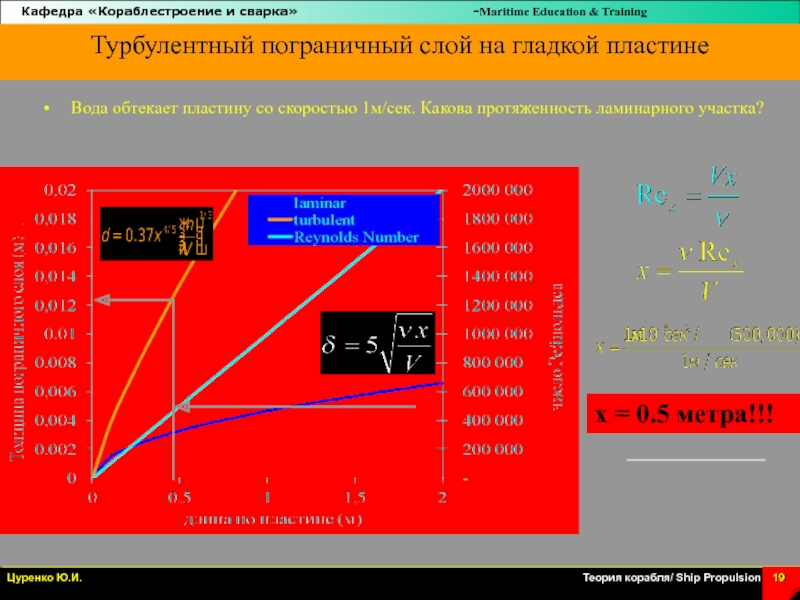
Слайд 19Турбулентный пограничный слой на гладкой пластине
Вода обтекает пластину со скоростью
1м/сек. Какова протяженность ламинарного участка?
x = 0.5 метра!!!
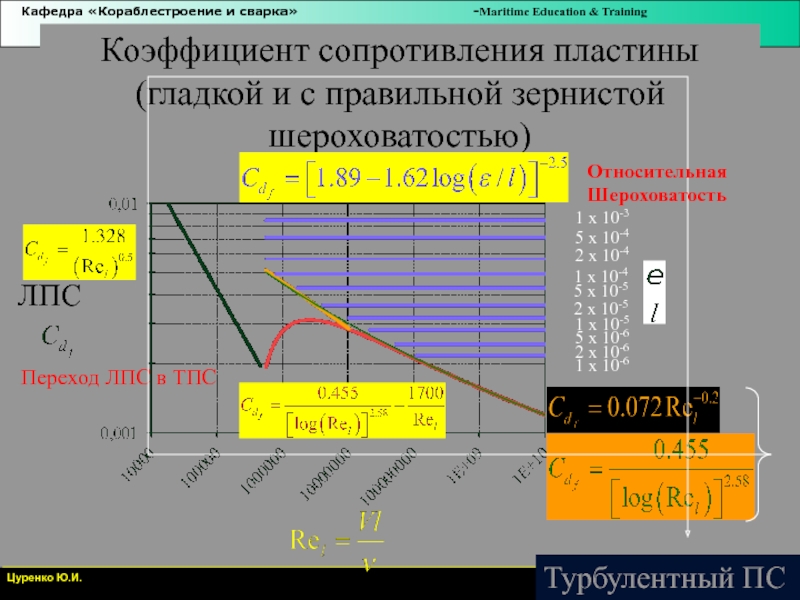
Слайд 20Коэффициент сопротивления пластины (гладкой и с правильной зернистой шероховатостью)
ЛПС
Переход ЛПС
в ТПС
Относительная Шероховатость
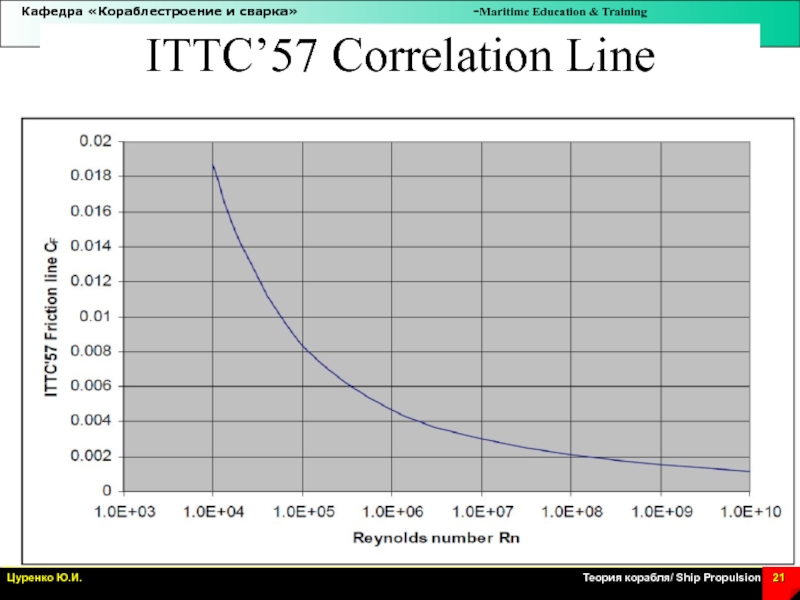
Слайд 21ITTC’57 Correlation Line
1.0E+03
1.0E+04
1.0E+05
1.0E+06 1.0E+07
Reynolds number Rn
1.0E+08
1.0E+09
1.0E+10
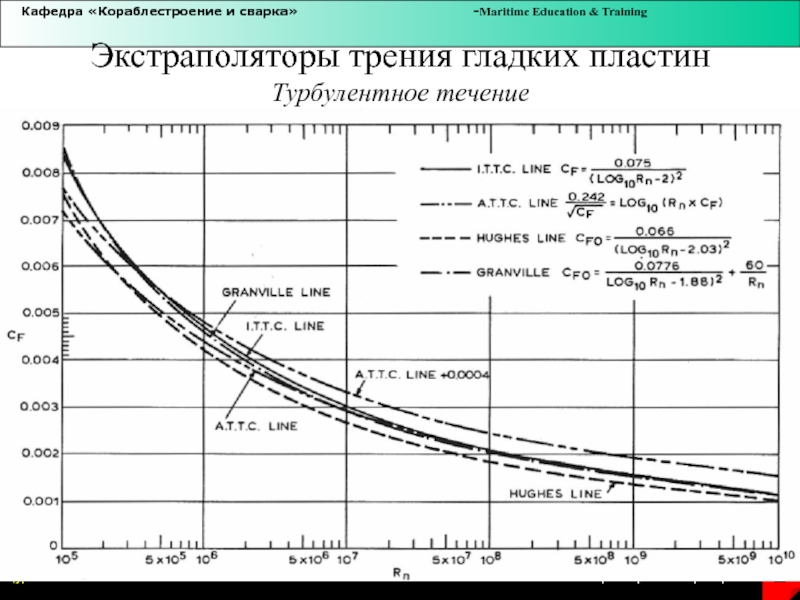
Слайд 22Экстраполяторы трения гладких пластин
Турбулентное течение
Слайд 23Влияние шероховатости на сопротивление трения
Технологическая шероховатость, обусловленная окраской, и эксплуатационная
шероховатость, вызванная разрушением краски, коррозией корпуса и его
обрастанием, представляют
собой случайные, сугубо нерегулярные процессы,
которые анализируются в форме профилограмм или по результатам измерений.
Эти процессы исследованы на опытных установках и судах и обработан
статистическими методами.
Технологическая шероховатость обшивки корпуса характеризуется высотой микронеровностей свежевыкрашенной поверхности, то есть равномерным распределением по поверхности микровыступов и микровпадин. К технологической шероховатости следует отнести сварные швы. Шероховатость свежеокрашенных поверхностей изменяется от 100 до 350 мкм. В результате испытаний судов установлено, что каждые 10 мкм шероховатости свежеокрашенного корпуса свыше 165 мкм увеличивают сопротивление корпуса или потребную мощность судна для достижения заданной скорости на 1%. При шероховатости более 230 мкм ее увеличение на каждые 10 мкм требует увеличения мощности на 0,5 %.
Коррозия и разрушение краски снижают скорость хода судов, увеличивают потребную мощность, повышают расход топлива. В среднем разрушение краски и коррозия приводят к уменьшению скорости хода на 10-25%.

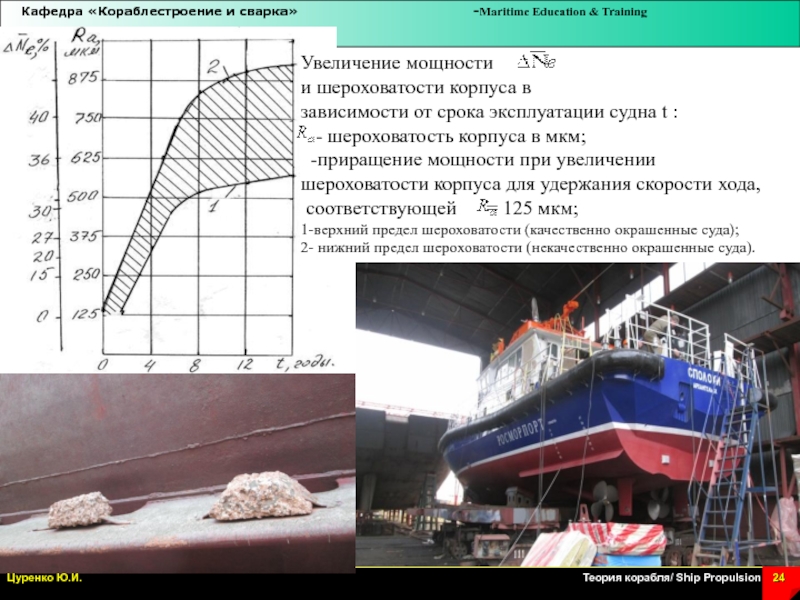
Слайд 24Увеличение мощности
и шероховатости корпуса в
зависимости от срока эксплуатации
судна t :
- шероховатость корпуса в мкм;
-приращение мощности при увеличении
шероховатости корпуса для удержания скорости хода,
соответствующей = 125 мкм;
1-верхний предел шероховатости (качественно окрашенные суда);
2- нижний предел шероховатости (некачественно окрашенные суда).
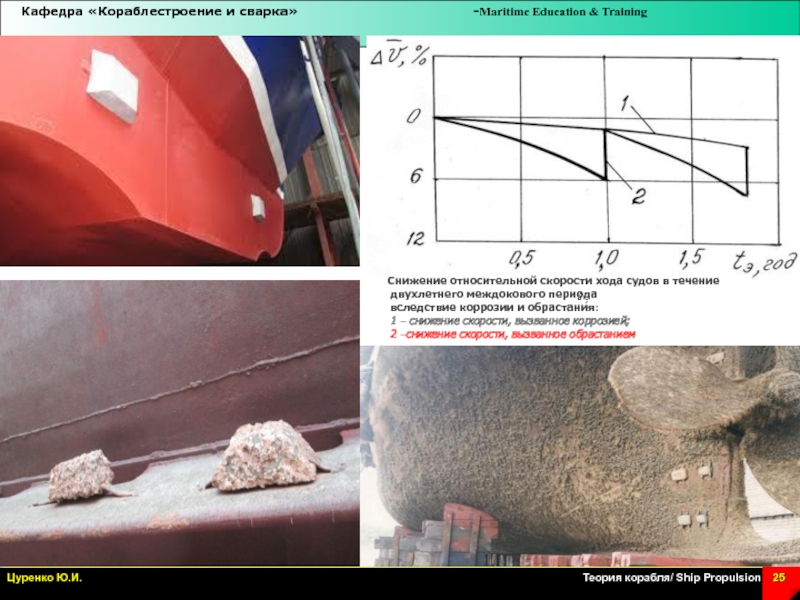
Слайд 25Снижение относительной скорости хода судов в течение
двухлетнего междокового периода
вследствие
коррозии и обрастания:
1 – снижение скорости, вызванное коррозией;
2 –снижение скорости, вызванное обрастанием
Слайд 26Пропульсивные качества судов ухудшаются с увеличением их возраста. Это объясняется
необратимым процессом увеличения шероховатости обшивки корпуса вследствие некачественной подготовки корпуса
перед окраской при очередных докованиях и вследствие усиления коррозии обшивки со сроком службы судна. Подводные очистки и очередные докования не восстанавливают полностью ходовых качеств судна.
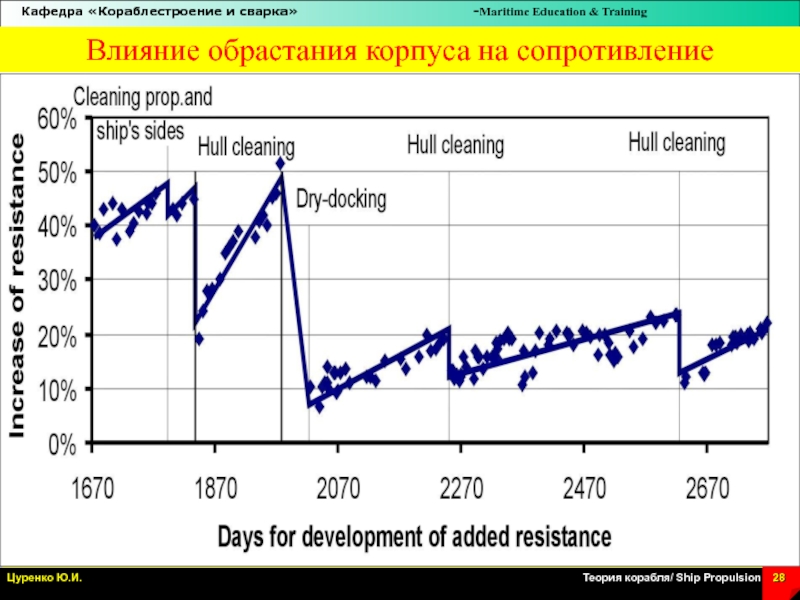
Слайд 28Влияние обрастания корпуса на сопротивление
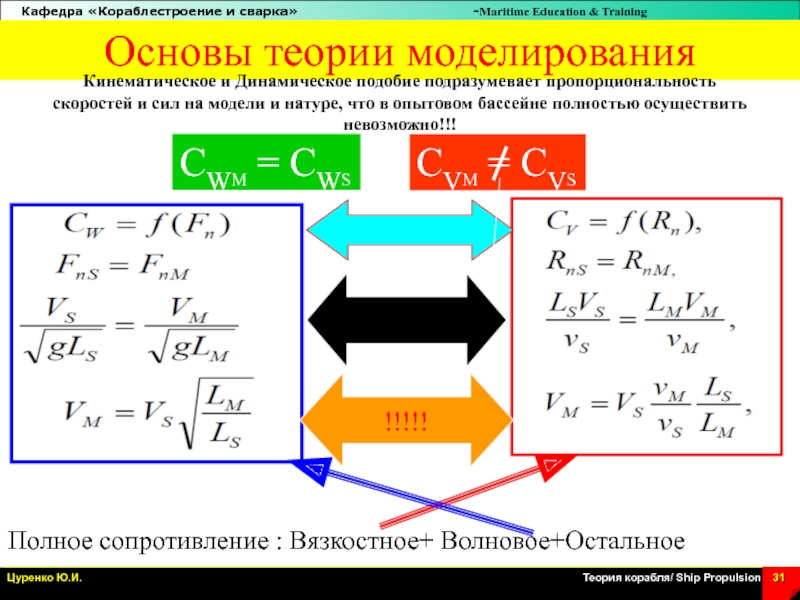
Слайд 31Основы теории моделирования
Кинематическое и Динамическое подобие подразумевает пропорциональность
скоростей и
сил на модели и натуре, что в опытовом бассейне полностью
осуществить невозможно!!!
Полное сопротивление : Вязкостное+ Волновое+Oстальное
!!!!!
Слайд 32Основы теории моделирования
В опытовом бассейне правильно моделируются только
волновые процессы,
а влияние вязкости приходится
учитывать приближенными методами
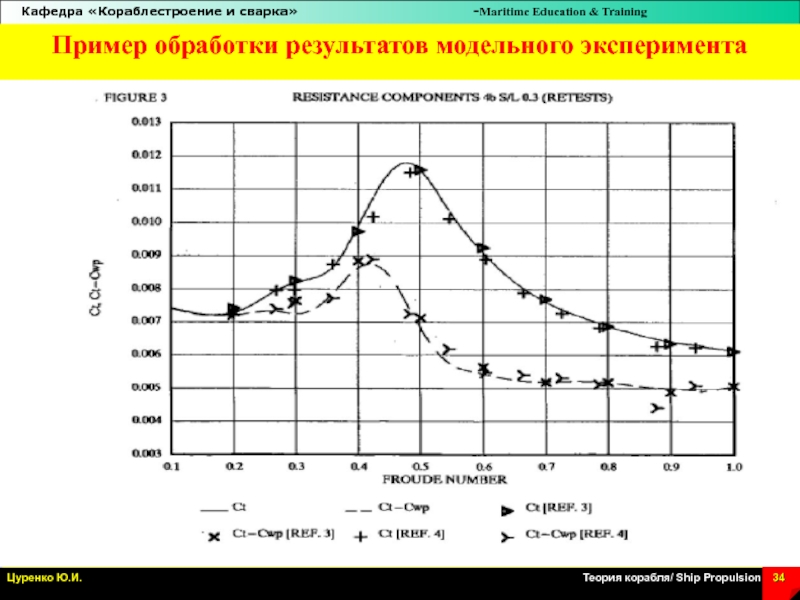
Слайд 34Пример обработки результатов модельного эксперимента
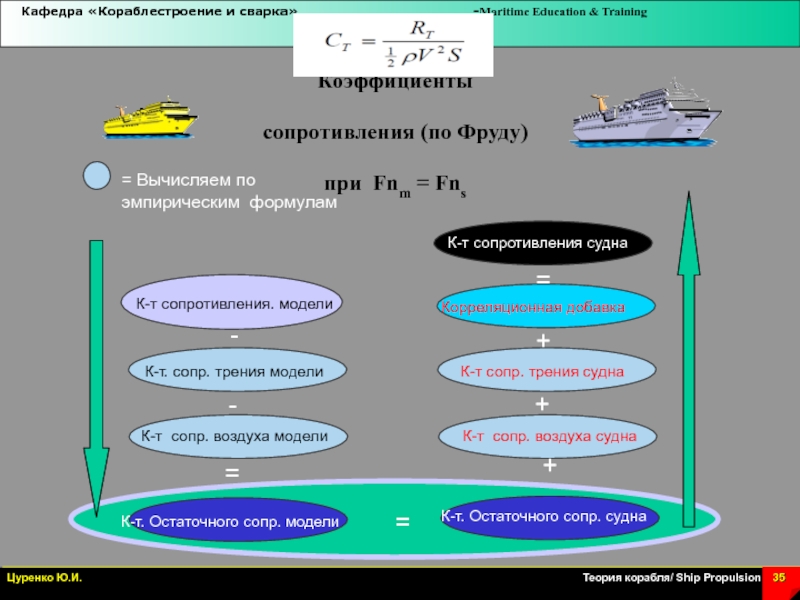
Слайд 35Коэффициенты сопротивления (по Фруду) при Fnm = Fns
К-т. сопр. трения
модели
К-т сопр. воздуха модели
К-т сопротивления. модели
-
К-т. Остаточного сопр. модели
=
=
-
Корреляционная добавка
К-т
сопр. трения судна
К-т сопр. воздуха судна
+
К-т. Остаточного сопр. судна
=
+
К-т сопротивления судна
+
= Вычисляем по эмпирическим формулам
Слайд 36 Объёмный удлинённый корпус судна при обтекании
водой создаёт систему избыточного скоростного давления, когда на большей части
длины оно отрицательное. В результате формируется тормозящий турбулентный пограничный слой и значительно растёт сопротивление трения (в носу, где избыточное давление положительное, обтекание ламинарное). Если же длину корпуса уменьшать, то существенно растёт сопротивление формы в результате неизбежного образования срывов потока и крупных вихрей, а также из-за образования вихревого следа.
Сопротивление формы
Слайд 37От положения точки отрыва пограничного слоя, т.е. места начала зарождения
вихрей, зависит величина вихревого сопротивления. Так, при тупых кормовых образованиях
тела точка отрыва приближается к миделю, область пониженного давления в кормовой части
становится шире, и, следовательно, сопротивление формы больше, чем в случае острых образований. Интенсивность образования вихревой системы обуславливает величину сопротивления формы. Это значит, что для уменьшения вихревого сопротивления тел необходимо либо вовсе устранить отрыв пограничного слоя , либо точку отрыва пограничного слоя по возможности сдвинуть к самой задней кромке тела, например, в судостроении для соблюдения этого положения еще в процессе проектирования выбирают определенные соотношения главных размерений и обводов судна, т.е. задают отношение L:B > 6 и длину кормового заострения
Обтекание корпусов кораблей
с разными формообразованиями
Для хорошо обтекаемых форм корпусов применяем гипотезу
аффинности составляющих вязкостного сопротивления
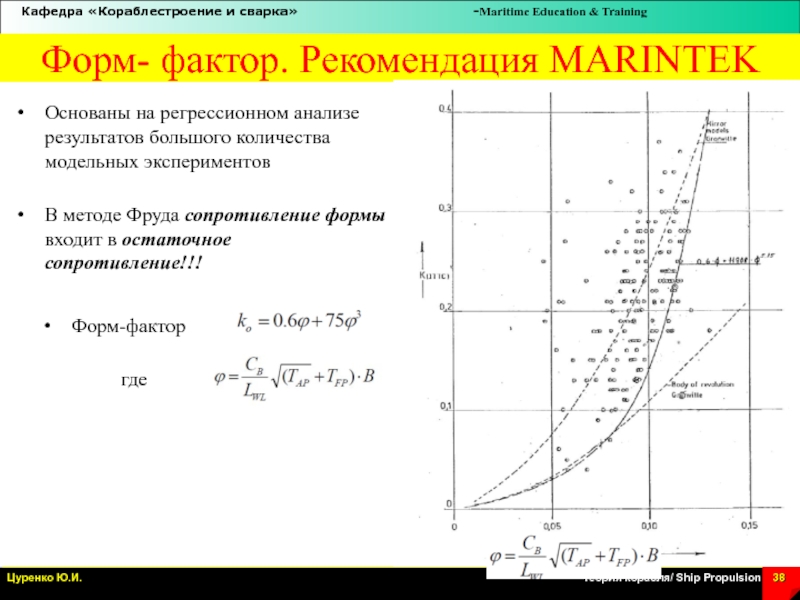
Слайд 38Форм- фактор. Рекомендация MARINTEK
Основаны на регрессионном анализе результатов большого
количества модельных экспериментов
В методе Фруда сопротивление формы входит в
остаточное сопротивление!!!
Форм-фактор
где
Слайд 39Коэффициенты сопротивления
(современная методика) при Fnm = Fns
Transom stern drag
Air
resistance
Определяем в модельном эксперименте
CRm CTm (1 ko )CFm
CAAm CBDm CRs
Residual resistance model
Residual resistance ship
=
CTs CRm (CFs CF )(1 ko ) CA CAAs CBDs
Measured model resistance
Viscous resistance
Full scale resistance
Viscous resistance
Air resistance
Вычисляем для натурного судна
Correlation coef
Transom stern drag
Слайд 40Вычисляемые коэффициенты сопротивления
Коэффициент сопротивления модели
Коэффициент сопротивления воздуха
Коэффициент сопротивления транца
Сопротивление выступающих
частей
Слайд 41Вычисляемые коэффициенты сопротивления
Вязкостное сопротивление
Сопротивление трения
Форм-фактор
Надбавка на шероховатость
(log R
2)2
0.075
C
n
F
(ITTC’57)
Слайд 42Корреляционный коэффициент CA
Вводится для компенсации систематических ошибок в принятом методе
пересчета результатов с модели на натуру
Изменяется в пределах (-0.15E-03
CA -0.3E-03) для водоизмещающих судов. Величина его также зависит от формы кормовой оконечности и выступающих частей.
В опытовых бассейнах к определению корреляционной надбавки («масштабного эффекта») подходят с особой тщательностью!
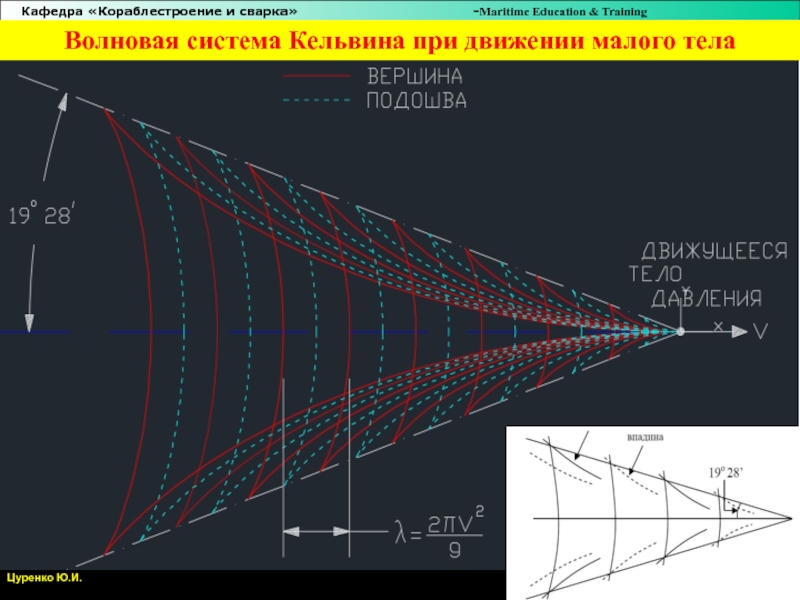
Слайд 43Волновое сопротивление
Лорд Кельвин в период 1887-1904 выполнил наблюдения характерных структур
волновой системы, включающей поперечные и расходящиеся волны, ограниченные
лучами под углом
19 градусов и 28 минут от диаметральной плоскости.
Слайд 45Волновая система Кельвина при движении малого тела
Слайд 46Волновая система Кельвина при движении малого тела
Слайд 47Распределение гидродинамических давлений вдоль корпуса движущегося судна неравномерно и характеризуется
повышением в оконечностях и понижением в районе миделя. Вследствие этого
форма поверхности воды искажается: там, где давление в потоке выше атмосферного, образуется бугор, а где оно ниже атмосферного - образуется впадина. Выведенные из положения равновесия частицы жидкости под действием сил тяжести и сил инерции стремятся вернуться в свое первоначальное положение. Это приводит к возникновению колебательного движения воды, внешним проявлением которого являются так называемые корабельные волны, образующиеся на спокойной поверхности воды.
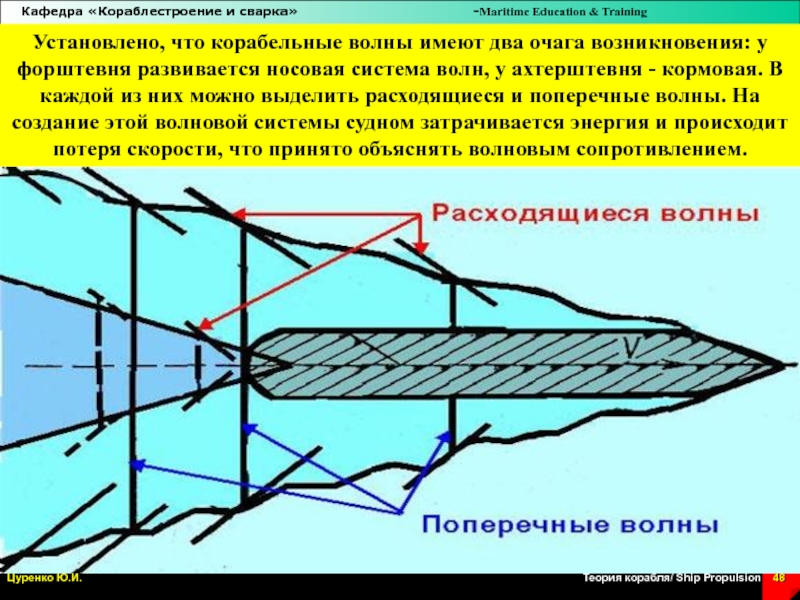
Слайд 48Установлено, что корабельные волны имеют два очага возникновения: у форштевня
развивается носовая система волн, у ахтерштевня - кормовая. В каждой
из них можно выделить расходящиеся и поперечные волны. На создание этой волновой системы судном затрачивается энергия и происходит потеря скорости, что принято объяснять волновым сопротивлением.
Слайд 49Пока скорость корабля неизменна, волны движутся вместе с ним, не
меняя ни величины, ни расположения. Если корабль идет малым ходом,
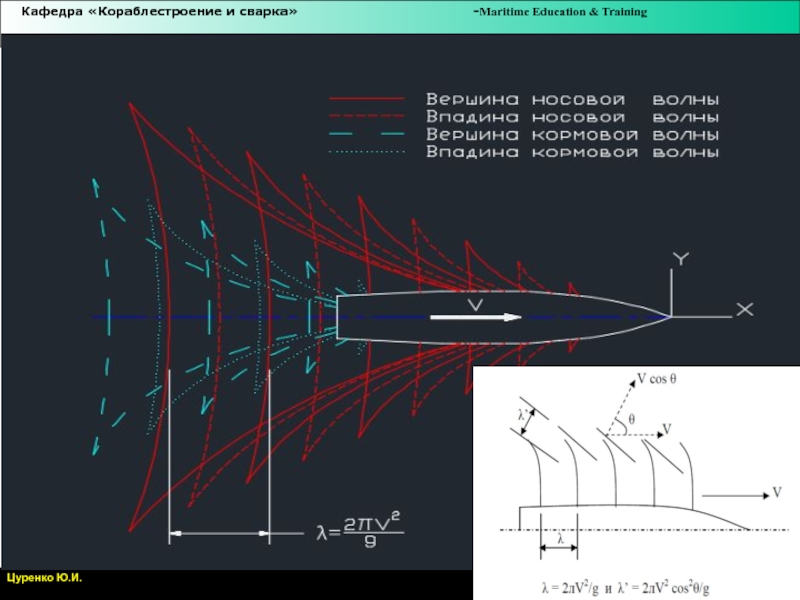
хорошо заметны расходящиеся волны, представляющие собой короткие валы, приблизительно параллельные друг другу, которые зарождаются в носовой и кормовой частях корабля. С увеличением скорости корабль сопровождают поперечные волны, располагающиеся между расходящимися, перпендикулярно к направлению курса, которые также зарождаются в носовой и кормовой частях корабля. На месте первой расходящейся волны в носовой части появляется бугор, который затем превращается в первую поперечную волну носовой системы волн.
Эта волна начинается гребнем, а первая поперечная волна кормовой системы волн — впадиной. Длина гребня у каждой последующей поперечной волны обеих систем больше, чем у предыдущей, а высота меньше. При значительном развитии поперечных волн расходящиеся теряют рельефность, а у быстроходных кораблей вообще становятся малозаметными.
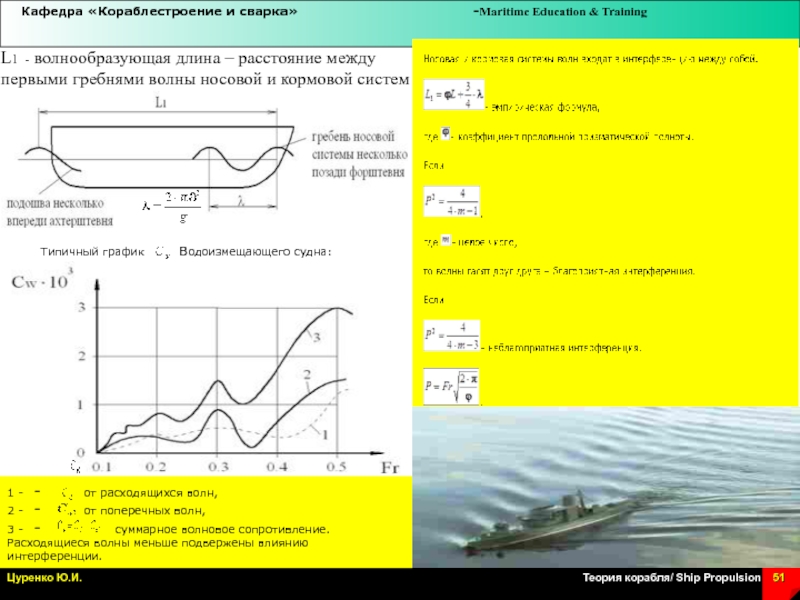
Слайд 51L1 - волнообразующая длина – расстояние между первыми гребнями волны
носовой и кормовой систем
Типичный график
водоизмещающего судна:
1 - - от расходящихся волн,
2 - - от поперечных волн,
3 - - суммарное волновое сопротивление.
Расходящиеся волны меньше подвержены влиянию интерференции.
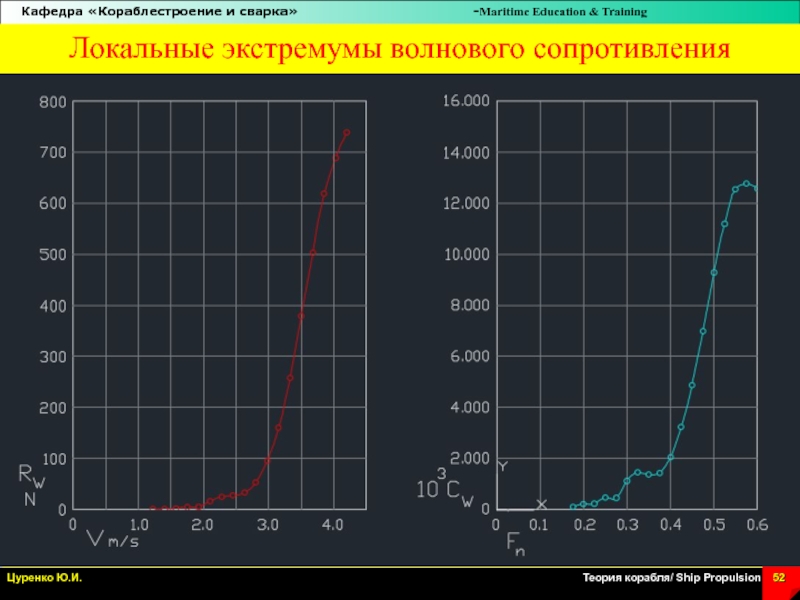
Слайд 52Локальные экстремумы волнового сопротивления
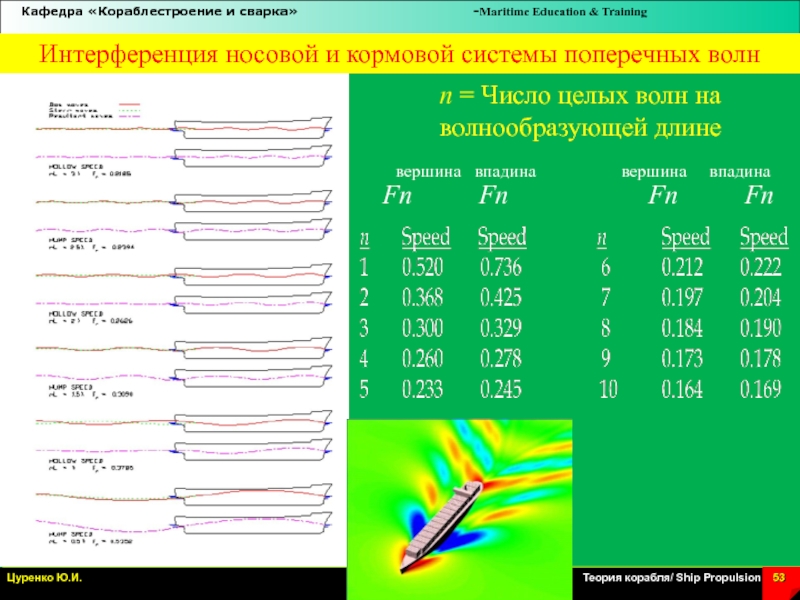
Слайд 53Интерференция носовой и кормовой системы поперечных волн
n = Число целых
волн на волнообразующей длине
вершина впадина
вершина впадина Fn Fn Fn Fn
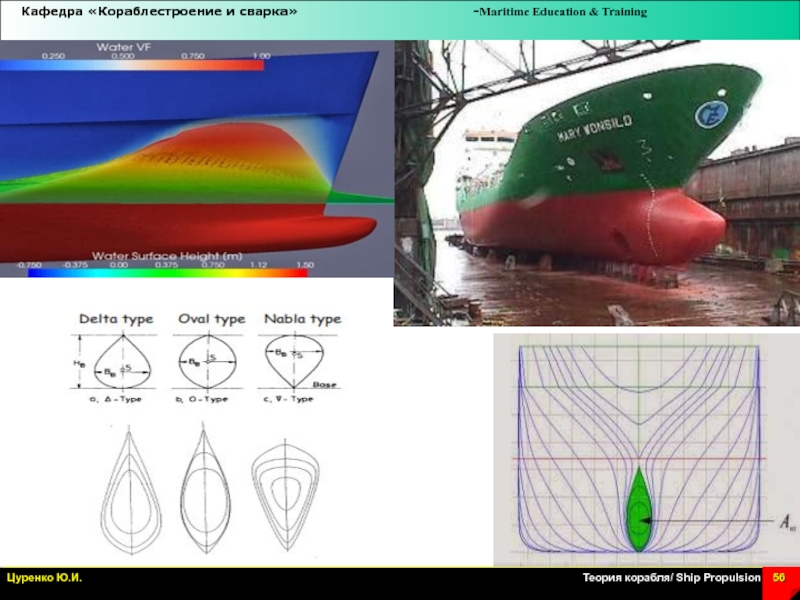
Слайд 54Носовой бульб
Носовой бульб при движении судна создает собственные волны,
которые интерферируют с поперечными волнами судна. В случае,
если такая
интерференция будет благоприятной (гребни одних волн
совпадают с подошвами других), то поверхность воды может
сглаживаться, тем самым происходит уменьшение сопротивления
воды движению судна. Здесь следует отметить, что длина
поперечной волны пропорциональна квадрату скорости судна,
поэтому при движении с разными скоростями интерференция может
быть не только благоприятной, но и неблагоприятной (когда гребни
одних волн совпадают с гребнями других), что вызывает увеличение
волн и тем самым увеличение сопротивления воды движению судна.
Слайд 55Геометрические характеристики бульба
Геометрические характеристики бульба: Lн.б – расстояние от
носового перпендикуляра судна до передней точки бульба;
н.б
– угол подъёма нижней кромки бульба над основной плоскостью судна, замеренный в районе носового перпендикуляра;
Нн.бп – высота передней точки бульба от основной плоскости;
Нн.б – наибольшая высота шпангоута наибольшей площади бульба;
Вн.б – наибольшая ширина бульба
Слайд 58Сопротивление выступающих частей
Выступающими частями судна считаются рули, кронштейны и выкружки
гребных валов, рудерпост, скуловые кили и т.д. Выступающие части создают
добавочное сопротивление Rapp которое определяется вязкостными составляющими. Если выступающие части рационально спроектированы и правильно расположены относительно корпуса, то их сопротивление вызывается силами трения. При нарушении этих требований резко возрастает сопротивление формы. Величина Rapp определяется экспериментально, путем сравнительных буксировочных испытаний модели судна с выступающими частями и без них в опытовых бассейнах.
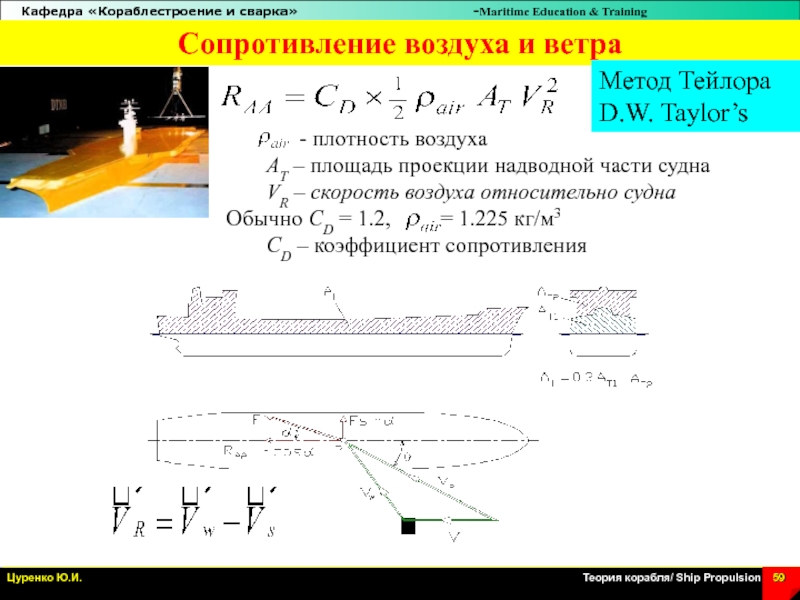
Слайд 59Сопротивление воздуха и ветра
- плотность воздуха
AT –
площадь проекции надводной части судна
VR – скорость воздуха относительно судна
Обычно
CD = 1.2, = 1.225 кг/м3
CD – коэффициент сопротивления
Метод Тейлора
D.W. Taylor’s
Слайд 60Воздушное сопротивление движению судна можно найти, испытывая модель надводной части судна
в аэродинамической трубе или стенде.
Модель судна помещают в рабочее
пространство и обдувают потоком воздуха, скорость которого может быть задана и измерена.
Сопротивление модели измеряют с помощью аэродинамических весов.
Сопротивление воздуха и ветра
Слайд 61Метод Хагеса (слегка модифицированный метод Тейлора) определяет компоненты RAA :
Сила
ветра:
VR = скорость воздуха относительно судна
= угол
результирующей с ДП
AL = площадь проекции надв. части на ДП
AT = площадь проекции надв. части на МШ
= угол силы ветра с ДП
Сопротивление воздуха и ветра
Метод Хагеса
Hughes method
Слайд 62Нельзя объять необъятное…
За пределами курса остались разделы, которые студент может
одолеть самостоятельно:
Сопротивление вырезов и отверстий
Сопротивление на волнении
Сопротивление в сплошном и
битом льду
Сопротивление на мелководье и в каналах
Сопротивление буксируемых объектов
Сопротивленин неводоизмещающих судов
Афоризм Козьмы Пруткова, из собрания мыслей и афоризмов «Плоды раздумья» (1854) , афоризм под номером 160 «Опять скажу: никто не обнимет необъятного!»