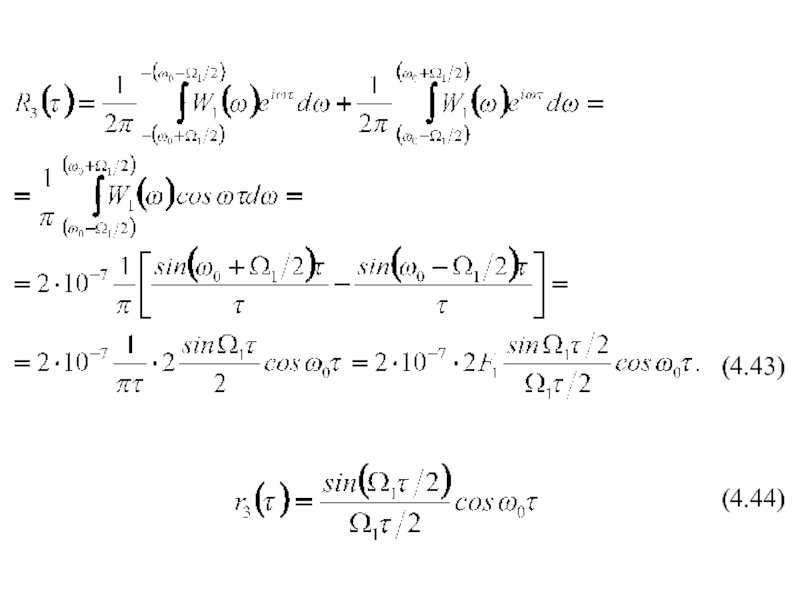среднюю мощность, приходящуюся на 1 Гц при заданной частоте ω.
Размерность функции W(ω), являющейся отношением мощности к
полосе частот, есть
(4.31)
(4.32)