Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
СПОСОБЫ ПРЕДСТАВЛЕНИЯ БУЛЕВЫХ ФУНКЦИЙ
Содержание
- 1. СПОСОБЫ ПРЕДСТАВЛЕНИЯ БУЛЕВЫХ ФУНКЦИЙ
- 2. Цель лекции – изучить способы представления булевых
- 3. Литература Горбатов В.А. Основы дискретной математики. М.:
- 4. ТерминыКлючевые слова: числовое, аналитическое, кубическое, схемотехническое представления
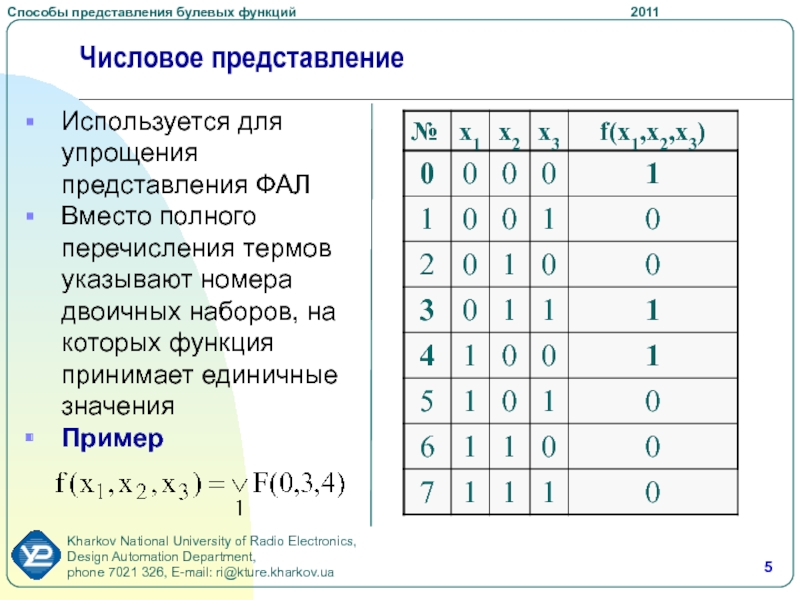
- 5. Числовое представлениеИспользуется для упрощения представления ФАЛВместо полного
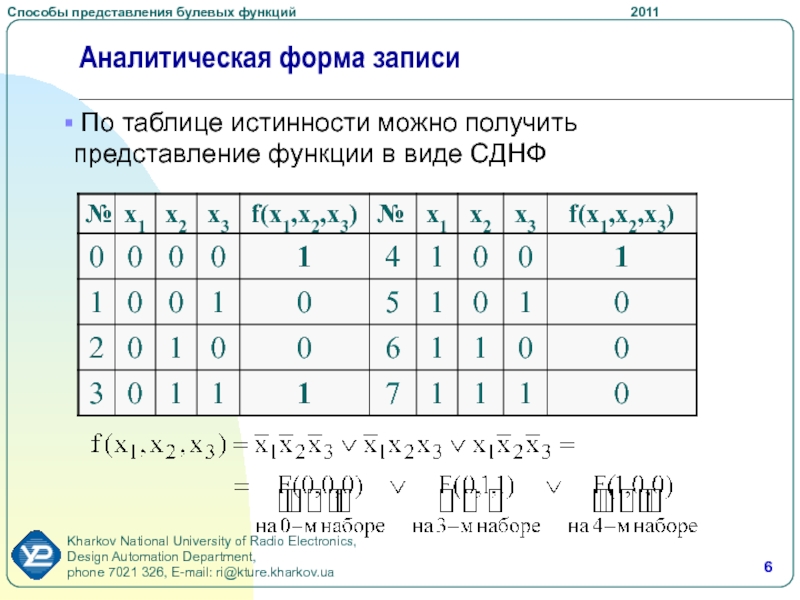
- 6. Аналитическая форма записи По таблице истинности можно получить представление функции в виде СДНФ
- 7. Геометрическое представление ФАЛИспользуется для интерпретации преобразований над логическими функциямиФАЛ от двух переменных изображают на плоскости
- 8. Геометрическое представление булевых функций от трех переменных.
- 9. Геометрическое представление булевых функций от трех переменных.
- 10. Пример геометрического представления ФАЛ Точками отмечаются вершины, в которых функция принимает единичное значение
- 11. Time-Out
- 12. Правила склеивания для функций от трех переменных
- 13. Кубическое представление ФАЛ Терм максимального ранга называется
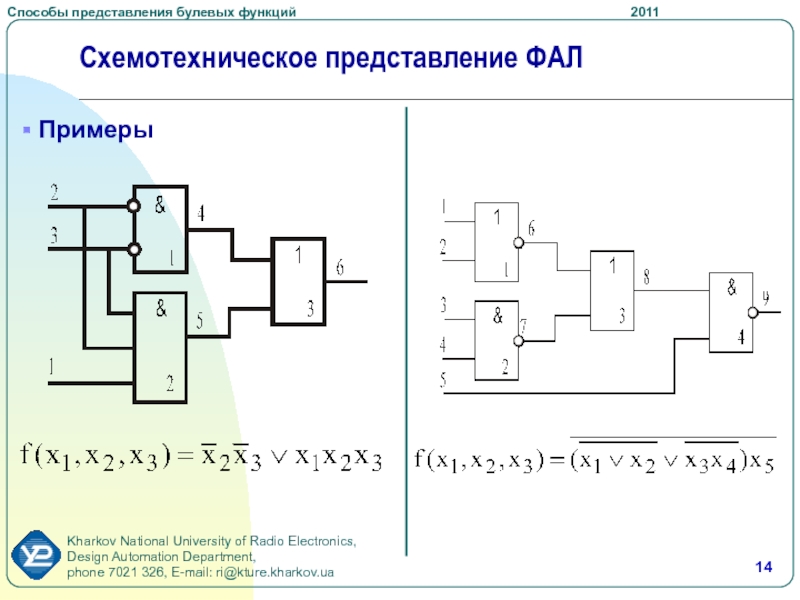
- 14. Схемотехническое представление ФАЛ Примеры
- 15. ВыводыДля описания одной и той же булевой
- 16. Тест-вопросы. 11.Какие из кубов представляют точку: а) 0-куб; б)
- 17. Тест-вопросы. 27. Какой элемент реализует функцию логического
- 18. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1СПОСОБЫ ПРЕДСТАВЛЕНИЯ БУЛЕВЫХ ФУНКЦИЙ
ЛЕКЦИЯ 10
В.И. ХАХАНОВ
Факультет компьютерной инженерии и
управления, кафедра АПВТ, ХНУРЭ
Слайд 2Цель лекции – изучить способы представления булевых функций для описания
цифровых проектов
Содержание:
Числовое представление булевых функций
Аналитическая форма записи
ФАЛГеометрическая интерпретация булевых функций
Кубическое представление
Схемотехническое представление
Тема: Способы представления булевых функций
Слайд 3Литература
Горбатов В.А. Основы дискретной математики. М.: Высш. шк., 1986.
32-61с.
Савельев А.Я. Прикладная теория цифровых автоматов. М.: Высш. шк.,
1987. 272 с.Беннеттс Р.Д. Проектирование тестопригодных логических схем: Пер. с англ. М.: Радио и связь. 1990. 176 с.
Бондаренко М.Ф., Кривуля Г.Ф., Рябцев В.Г., Фрадков С.А., Хаханов В.И. Проектирование и диагностика компьютерных систем и сетей. К.: НМЦ ВО. 2000. 306 с.
Богомолов А.М., Сперанский Д.В. Аналитические методы в задачах контроля и анализа дискретных устройств. Саратов: Изд-во Саратовкого ун-та, 1986. 240с.
Хаханов В.И. Техническая диагностика элементов и узлов персональных компьюторов. К.: ИСМО, 1997. 308 с.
Хаханов В.І., Хаханова І.В., Кулак Е.М., Чумаченко С.В. Методичні вказівки до практичних занять з курсу “Дискретна математика”. Харків, ХНУРЕ. 2001. С.31-35.
Новиков Ф.А. Дискретная математика для программистов. С.-П., 2001. С. 263-268.
Слайд 4Термины
Ключевые слова:
числовое,
аналитическое,
кубическое,
схемотехническое представления булевых функций
Базовые
понятия:
булева переменная,
булева функция,
двоичная система счисления,
закон склеиванияСлайд 5Числовое представление
Используется для упрощения представления ФАЛ
Вместо полного перечисления термов указывают
номера двоичных наборов, на которых функция принимает единичные значения
Пример
Слайд 6Аналитическая форма записи
По таблице истинности можно получить представление функции
в виде СДНФ
Слайд 7Геометрическое представление ФАЛ
Используется для интерпретации преобразований над логическими функциями
ФАЛ от
двух переменных изображают на плоскости
Слайд 8Геометрическое представление булевых функций от трех переменных. 1
Для функции
трех переменных геометрическое представление выполняют в виде куба
Вершины обозначаются:
десятичными цифрамидвоичными цифрами
произвольными переменными
Ребра куба поглощают вершины
Грани куба поглощают ребра
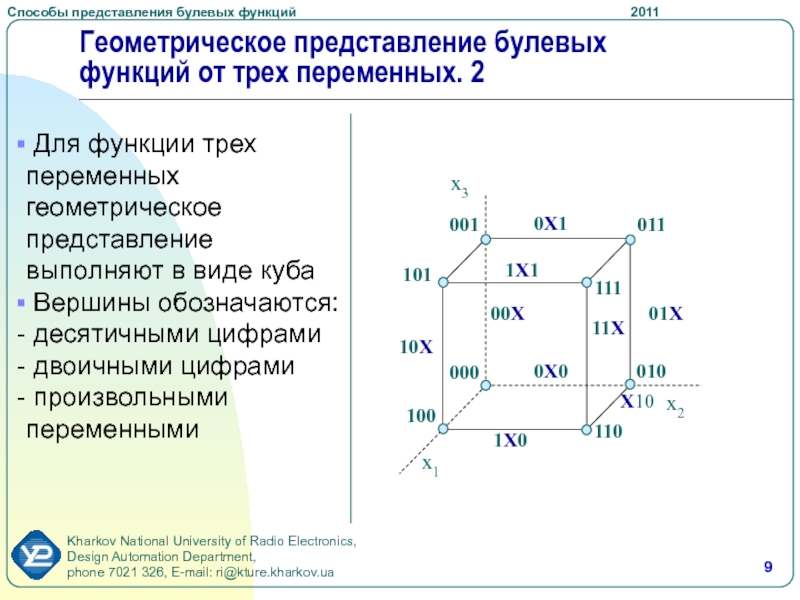
Слайд 9Геометрическое представление булевых функций от трех переменных. 2
Для функции
трех переменных геометрическое представление выполняют в виде куба
Вершины обозначаются:
десятичными цифрамидвоичными цифрами
произвольными переменными
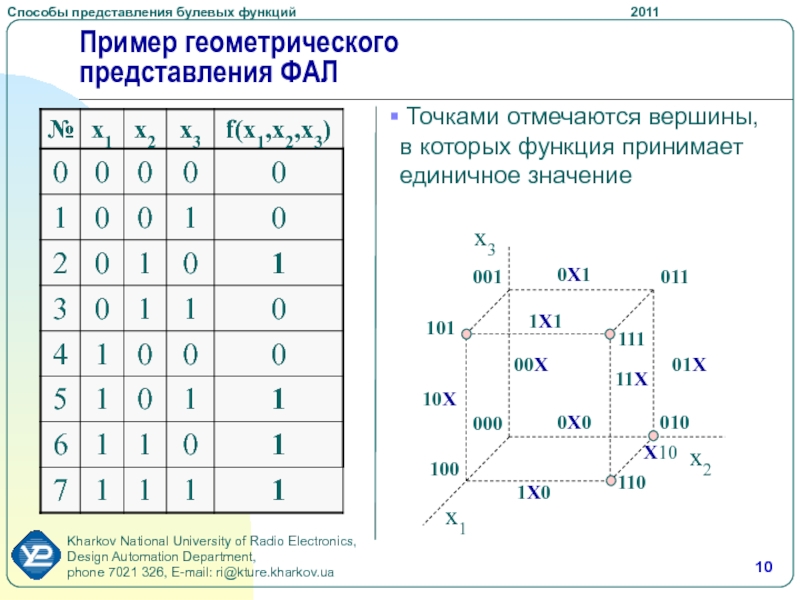
Слайд 10Пример геометрического представления ФАЛ
Точками отмечаются вершины, в которых функция
принимает единичное значение
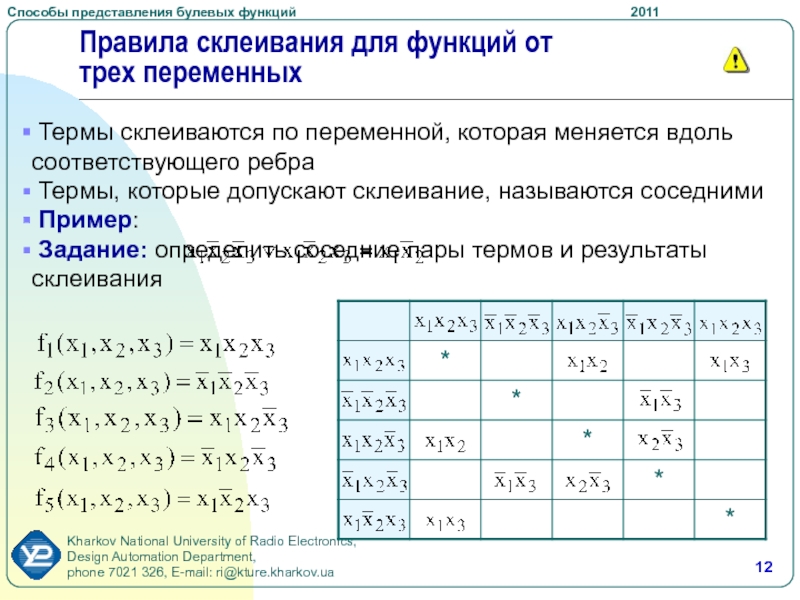
Слайд 12Правила склеивания для функций от трех переменных
Термы склеиваются по
переменной, которая меняется вдоль соответствующего ребра
Термы, которые допускают склеивание,
называются соседними Пример:
Задание: определить соседние пары термов и результаты склеивания
Слайд 13Кубическое представление ФАЛ
Терм максимального ранга называется 0-кубом или точкой
Склеивание 0-кубов = отрезок (1-куб)
Склеивание отрезков = грань (2-куб)
Склеивание граней = кубПример
Слайд 15Выводы
Для описания одной и той же булевой функции используются различные
способы ее представления
Способы представления ФАЛ зависят от решаемых задач
Числовое представление
используется для упрощения формы записи ФАЛ и основывается на десятичных эквивалентах двоичных наборовВ геометрическом смысле каждый двоичный набор может рассматриваться как n-мерный двоичный вектор, определяющий точку n-мерного пространства. Множество наборов, на которых определена функция, представляется в виде вершин n-мерного куба
Кубическое представление используется при минимизации булевых функций, в частности, в методе Квайна-Мак-Класки
Слайд 16Тест-вопросы. 1
1.Какие из кубов представляют точку:
а) 0-куб; б) 1-куб;
в) 2-куб; г) любой.
2.Какие
из кубов задают отрезок:
а) 0-куб; б) 1-куб;
в) 2-куб; г) любой.
3.Какие из кубов
представляют плоскость:а) 0-куб; б) 1-куб;
в) 2-куб; г) любой.
4. Указать куб, который геометрически можно интерпретировать как плоскость:
а) Х00; б) 0ХХ;
в) 101; г) любой.
5. Указать куб, который геометрически можно интерпретировать как отрезок:
а) Х0Х; б) 01Х;
в) 101; г) любой.
6. Указать куб, который геометрически можно интерпретировать как точку:
а) 100; б) 0ХХ;
в) 10Х; г) любой.
Слайд 17Тест-вопросы. 2
7. Какой элемент реализует функцию логического сложения:
а) б) в) г)
8. Какой элемент
реализует функцию логического умножения:
а) б) в) г)
9. Какой элемент реализует функцию сложения по
модулю 2:а) б) в) г)