Слайд 1Способы представления дисперсионного соотношения
Последний вопрос – как представить дисперсионное соотношение?
1.
аналитическое выражение, хотя бы приближенное; удобно для рутинных расчетов, но
редко дает наглядное представление;
2. табличный, удобен для повседневного пользования, но громоздок и не нагляден;
3. графический, отличается наглядностью, но обладает малой точностью.
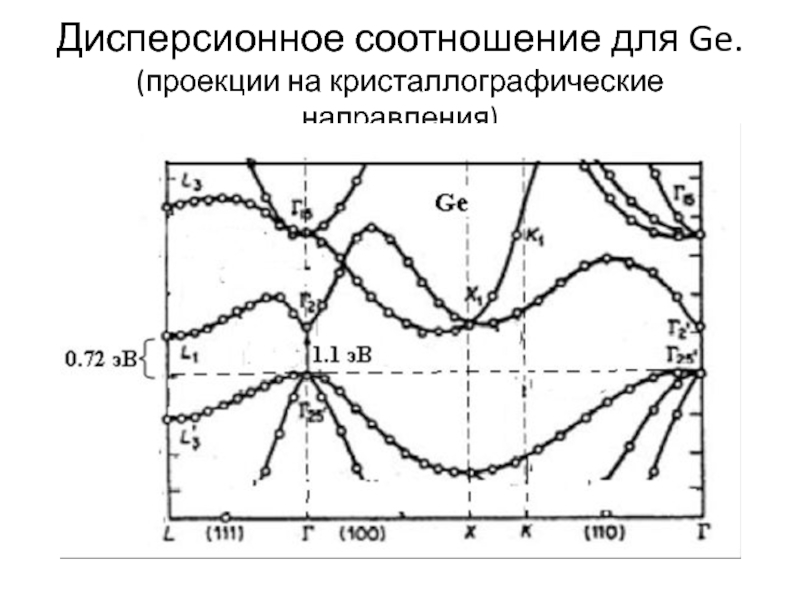
Слайд 2Дисперсионное соотношение для Ge.
(проекции на кристаллографические направления)
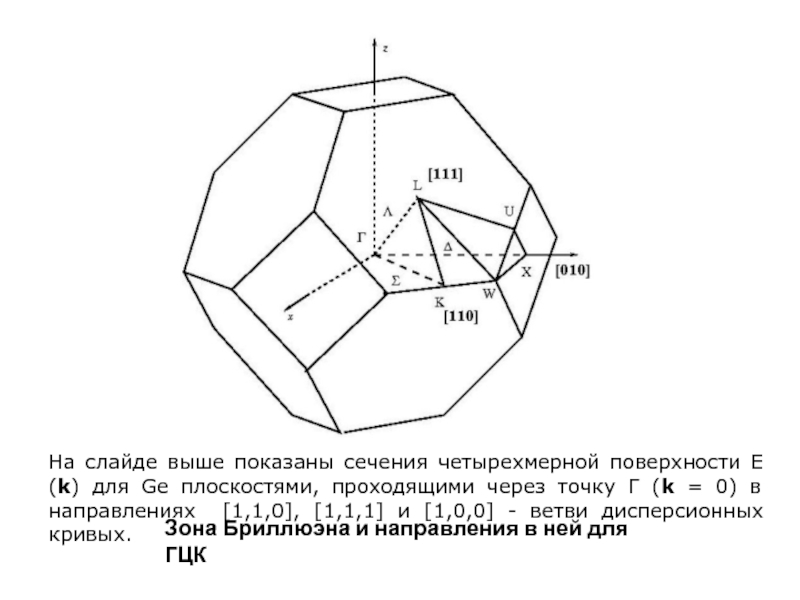
Слайд 3Зона Бриллюэна и направления в ней для ГЦК
На слайде выше
показаны сечения четырехмерной поверхности Е(k) для Ge плоскостями, проходящими через
точку Г (k = 0) в направлениях [1,1,0], [1,1,1] и [1,0,0] - ветви дисперсионных кривых.
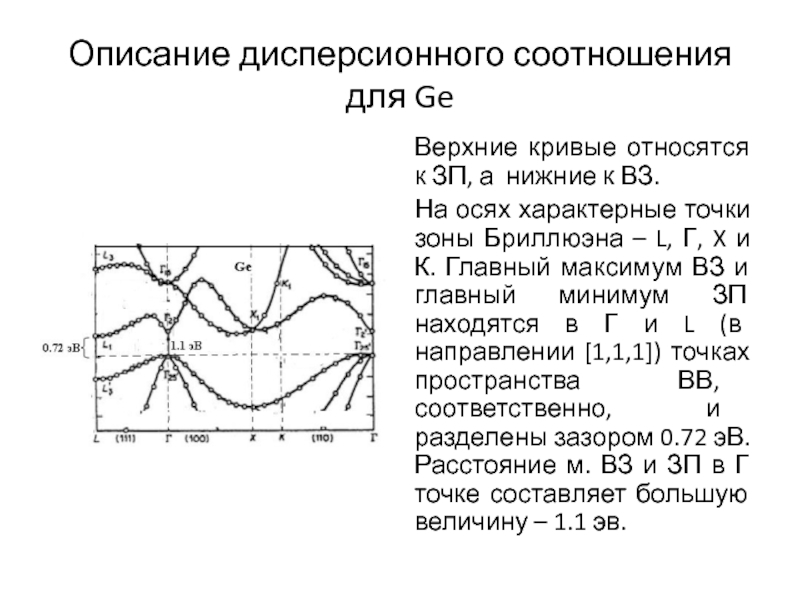
Слайд 4Описание дисперсионного соотношения
для Ge
Верхние кривые относятся к ЗП, а
нижние к ВЗ.
На осях характерные точки зоны Бриллюэна –
L, , X и К. Главный максимум ВЗ и главный минимум ЗП находятся в и L (в направлении [1,1,1]) точках пространства ВВ, соответственно, и разделены зазором 0.72 эВ. Расстояние м. ВЗ и ЗП в точке составляет большую величину – 1.1 эв.
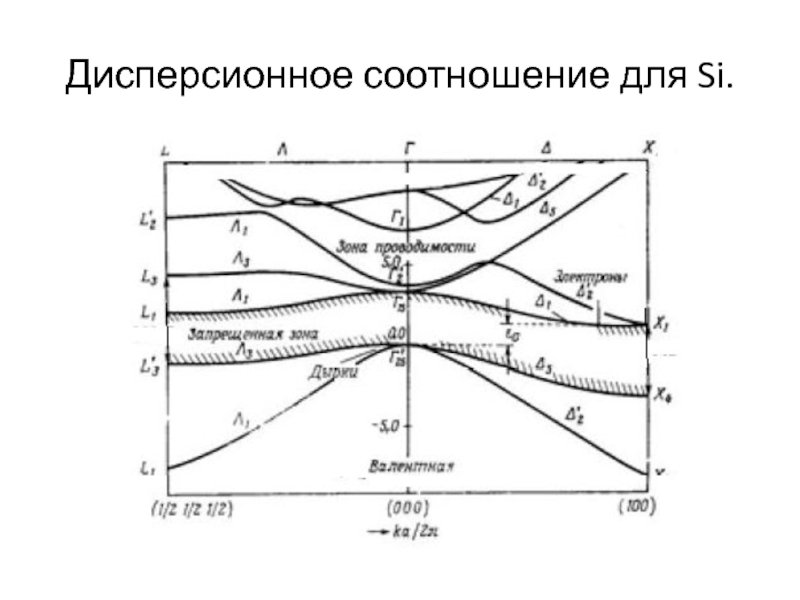
Слайд 5Дисперсионное соотношение для Si.
Слайд 6Иэоэнергетические эллипсоиды.
Другой графический способ годится только для окрестностей экстремальных точек
зависимостей E(k), где изоэнергетические пов-ти близки к эллипсоидам. Они и
изображаются в аксонометрической проекции в пространстве ВВ. Такой способ менее информативен, но более нагляден.
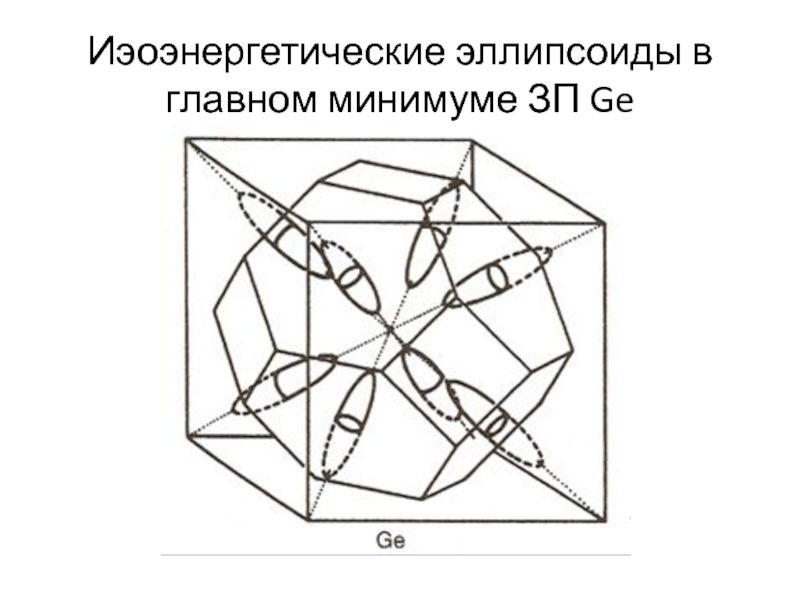
Слайд 7Иэоэнергетические эллипсоиды в главном минимуме ЗП Ge
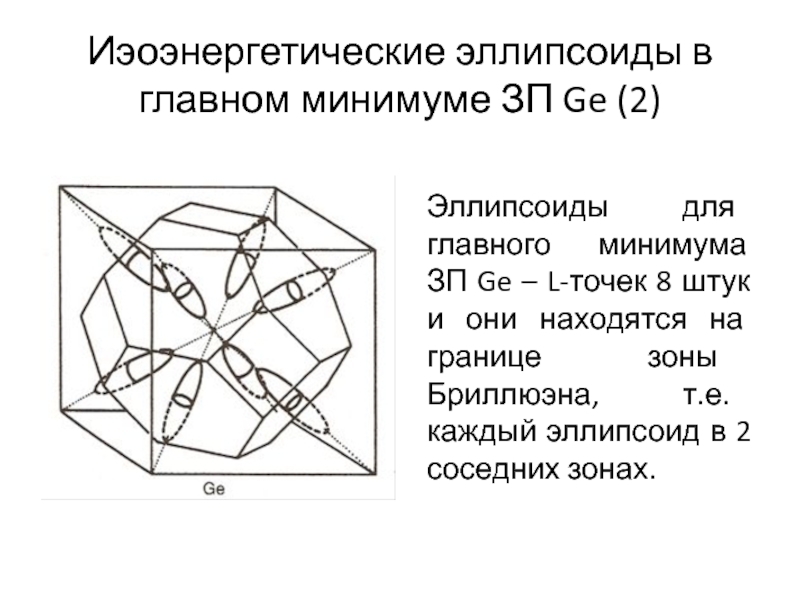
Слайд 8Иэоэнергетические эллипсоиды в главном минимуме ЗП Ge (2)
Эллипсоиды для главного
минимума ЗП Ge – L-точек 8 штук и они находятся
на границе зоны Бриллюэна, т.е. каждый эллипсоид в 2 соседних зонах.
Слайд 9Иэоэнергетические эллипсоиды в главном минимуме ЗП Si
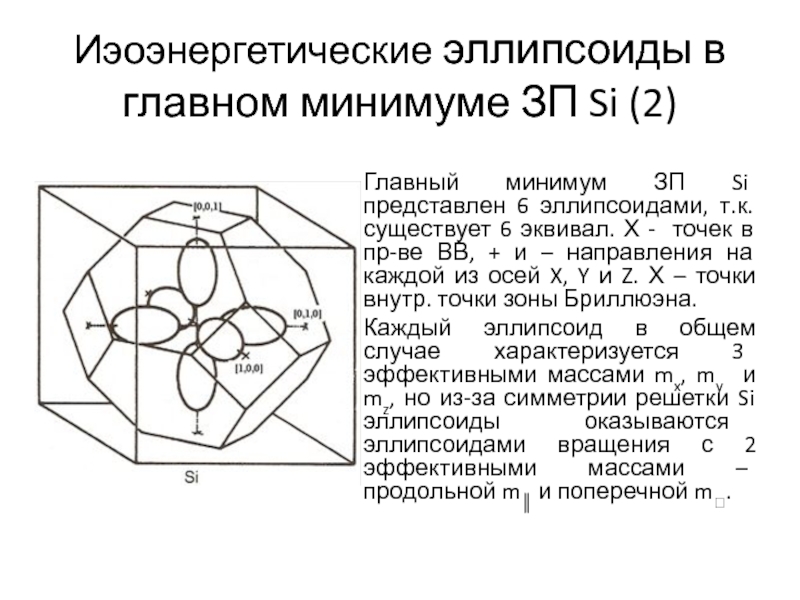
Слайд 10Иэоэнергетические эллипсоиды в главном минимуме ЗП Si (2)
Главный минимум ЗП
Si представлен 6 эллипсоидами, т.к. существует 6 эквивал. Х -
точек в пр-ве ВВ, + и – направления на каждой из осей X, Y и Z. Х – точки внутр. точки зоны Бриллюэна.
Каждый эллипсоид в общем случае характеризуется 3 эффективными массами mx, my и mz, но из-за симметрии решетки Si эллипсоиды оказываются эллипсоидами вращения с 2 эффективными массами – продольной m║ и поперечной m.
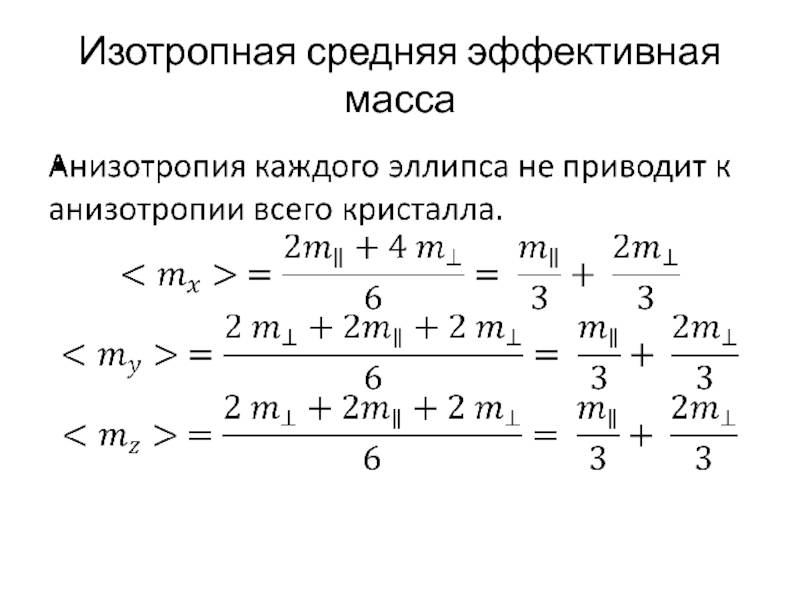
Слайд 11Изотропная средняя эффективная масса
Слайд 13Эффективные массы
в ед. массы электрона
Зона пров. Вал. зона
Eg, эВ m║ m m║ m
Ge 0.72 1.58(L) 0.08 (L) 0.34(Г) 0.04 (Г)
Si 1.11 0.98 () 0.19 () 0.50 (Г) 0.17 (Г)
GaAs 1.41 0.04 (Г) 0.5 (Г) 0.12 (Г)
InSb 0.18 0.01 (Г) 0.3 (Г) 0.02 (Г)
InAs 0.36 0.026 (Г) 0.82 (Г) 0.025 (Г)
GaP 2.24 0.13 (L) 0.56 (Г) 0. 2 (Г)