Слайд 1СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИСТЕМ УПРАВЛЕНИЯ
Виды статических характеристик.
Режим работы систем,
в котором управляемая и все промежуточные величины не изменяются во
времени, называется статическим (установившимся) и описывается уравнениями зависимости выходного состояния объекта управления от постоянных (независимых от времени) значений управляющих воздействий u и любых других дестабилизирующих факторов f.
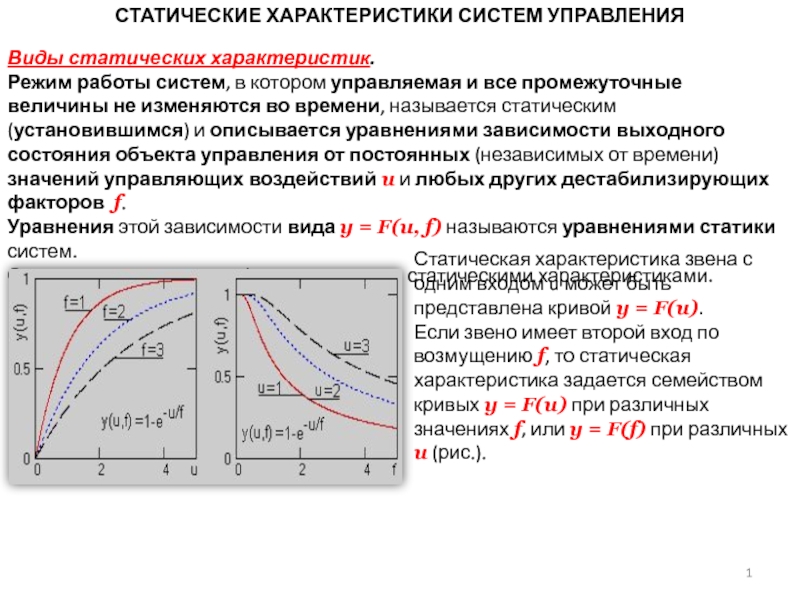
Уравнения этой зависимости вида y = F(u, f) называются уравнениями статики систем.
Соответствующие им графики называются статическими характеристиками.
Статическая характеристика звена с одним входом u может быть представлена кривой y = F(u).
Если звено имеет второй вход по возмущению f, то статическая характеристика задается семейством кривых y = F(u) при различных значениях f, или y = F(f) при различных u (рис.).
Слайд 2Примером функционального звена системы регулирования уровня воды в баке может
быть обычный рычаг с поплавком.
Уравнение статики для него имеет
вид y = K u. Функцией звена является усиление (или ослабление) входного сигнала в K раз.
Коэффициент K = y/u, равный отношению выходной величины к входной, называется коэффициентом усиления звена.
Если входная и выходная величины имеют разную природу, его называют коэффициентом передачи.
Звенья с линейными статическими характеристиками называются линейными.
Статические характеристики реальных звеньев систем, как правило, нелинейные.
Для них характерна зависимость коэффициента передачи от величины входного сигнала:
K= Dy/ Du ≠ const,
которая может быть выражена какой-либо математической зависимостью, задаваться таблично или графически.
Если все звенья системы линейные, то система имеет линейную статическую характеристику.
Если хотя бы одно звено нелинейное, то система нелинейная.
Виды статических характеристик (продолжение).
Слайд 3Статическое и астатическое регулирование.
Если на управляемый процесс действует возмущение
(дестабилизирующий фактор) f, то значение имеет статическая характеристика системы в
форме y = F(f) при y0 = const.
Возможны два характерных вида этих характеристик (рис.). В соответствии с тем, какая из двух характеристик свойственна данной системе, различают статическое и астатическое регулирование.
Рассмотрим систему регулирования уровня воды в баке. Возмущающим фактором системы является поток Q воды из бака.
Пусть при Q = 0 имеем y = y0, сигнал рассогласования по заданному уровню воды e = 0.
Звено управления Р системы (регулятор) настраивается так, чтобы вода при этом в бак не поступала.
При Q ≠ 0, уровень воды понижается (e ≠ 0), поплавок опускается и открывает заслонку, в бак начинает поступать вода.
Новое состояние равновесия достигается при равенстве входящего и выходящего потоков воды.
Следовательно, при Q ≠ 0 заслонка должна быть обязательно открыта, что возможно только при каком-то новом уровне воды y1, при котором e = К (y0-y1) ≠ 0. Причем, чем больше Q, тем при больших значениях e устанавливается новое равновесное состояние. Статическая характеристика системы имеет характерный наклон (рис. б).

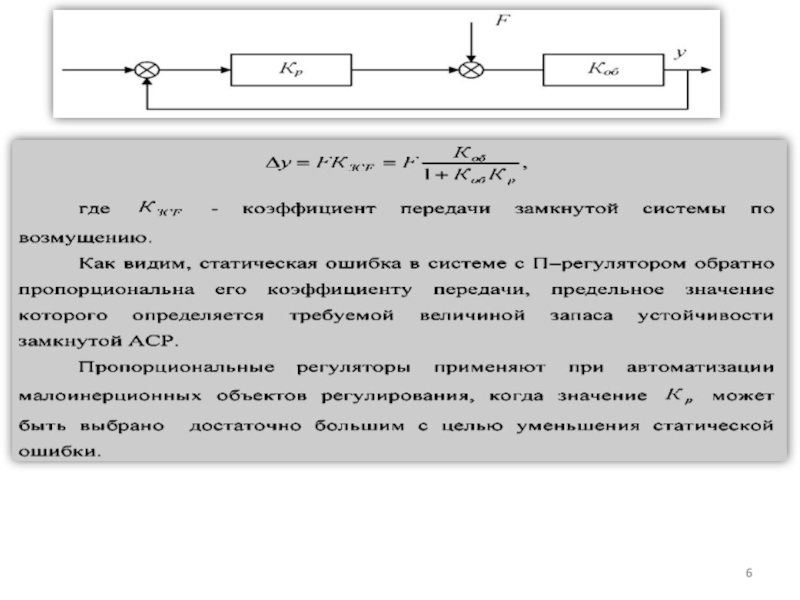
Слайд 4Статические регуляторы работают при обязательном отклонении e регулируемой величины y
от требуемого значения у0. Это отклонение тем больше, чем больше
возмущение f, и называется статической ошибкой регулятора.
Чем больше коэффициент передачи К регулятора, тем на большую величину будет открываться заслонка при одних и тех же значениях e, обеспечивая большую величину потока Q, при этом статическая характеристика системы пойдет более полого. Поэтому для уменьшения статической ошибки надо увеличивать коэффициент передачи регулятора.
Этот параметр регулирования получил название статизма d и равен тангенсу угла a наклона статической характеристики, построенной в относительных единицах:
d = tg(a) = (Dy/yн) / (Df/fн),
где yн, fн - точка номинального режима системы.
При достаточно больших значениях К имеем d 1/K.
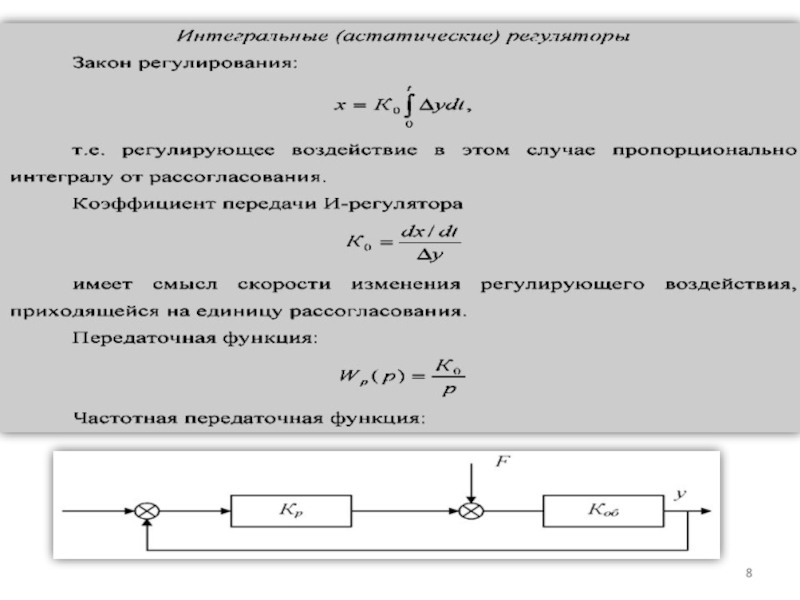
Слайд 7Астатический регулятор применяется, если статическая ошибка регулирования недопустима и регулируемая
величина должна поддерживать постоянное требуемое значение независимо от величины возмущающего
фактора.
Статическая характеристика астатической системы не имеет наклона.
Для того чтобы получить астатическое регулирование, необходимо в регулятор включить астатическое звено.
Астатическое звено отличается тем, что каждому значению входной величины может соответствовать множество значений выходной величины.
Так, для регулирования уровня воды в астатическом режиме может быть применен импульсный двигатель.
Если уровень воды понизится, то появившееся значение e > 0 включит импульсный двигатель и он начнет открывать заслонку до тех пор, пока значение e не станет равным нулю (по определенному порогу).
При поднятии уровня воды значение e сменит знак, и запустит двигатель в противоположную сторону, опуская заслонку.
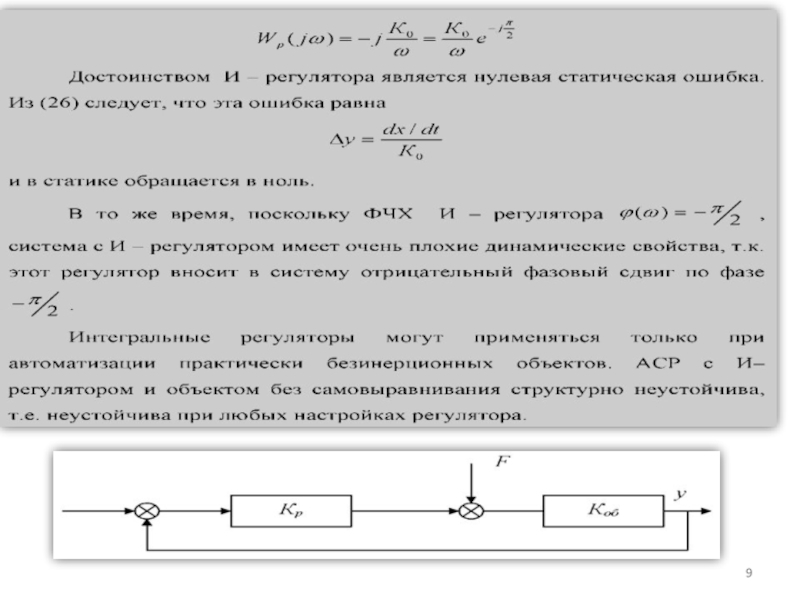
Астатические регуляторы не имеют статической ошибки, но они инерционны, сложны конструктивно и более дороги.
Обеспечение требуемой статической точности регулирования является первой основной задачей при расчете элементов системы управления.

Слайд 10ДИНАМИЧЕСКИЙ РЕЖИМ СИСТЕМ
Обычно на управляемый процесс действуют различные возмущения, отклоняющие
управляемый параметр от заданной величины.
Установившийся режим является не более
чем частным случаем состояния системы на определенных временных интервалах ее работы.
Процесс установления требуемого значения управляемой величины называется регулированием, и, ввиду инерционности звеньев регулирования, развивается во времени.
Динамическим называется режим работы системы, при котором входная и выходная величины системы изменяются во времени.
Как правило, динамический режим возникает в результате перехода системы от одного установившегося состояния к другому, и поэтому его часто называют переходным режимом, а процесс перехода от одного установившегося состояния к другому - переходным процессом.
Типичный пример переходных процессов для статических и астатических систем приведен на рис.
Динамический режим, характеризующийся протеканием в ней определенных переходных процессов, является основным режимом работы систем.
Зависимость выходной величины от изменяющейся во времени входной величины называют динамической характеристикой системы.

Слайд 11Все динамические характеристики можно разделить на две группы.
К первой
группе относятся зависимости выходной величины системы от времени, если входная
величина изменяется по типовому закону (импульсный, линейный и т.п.). Это так называемые временные характеристики.
Вторую группу динамических характеристик составляют частотные характеристики.
К ним относятся зависимости выходной величины или ее параметров от частоты входной величины, изменяющейся по гармоническому закону.
Переходные процессы в системе.
Зависимость выходной величины системы от времени, если входная величина изменилась на единый скачок, называют переходной характеристикой.
Допустим, система находится в установившемся режиме, и имеет значение выходной величины y = y0.
Пусть в момент t = 0 на объект воздействовал какой-либо управляющий или возмущающий фактор x(t), отклонив значение регулируемой величины от номинальной.
Через некоторое время регулятор вернет систему к первоначальному состоянию (с учетом статистической ошибки).
Если этот переходной процесс происходит по апериодическому временному закону, то процесс регулирования называется апериодическим.
При резких возмущениях в системах возможен колебательный затухающий процесс, а в неустойчивых системах - возникновение незатухающих колебаний и расходящийся колебательный процесс.
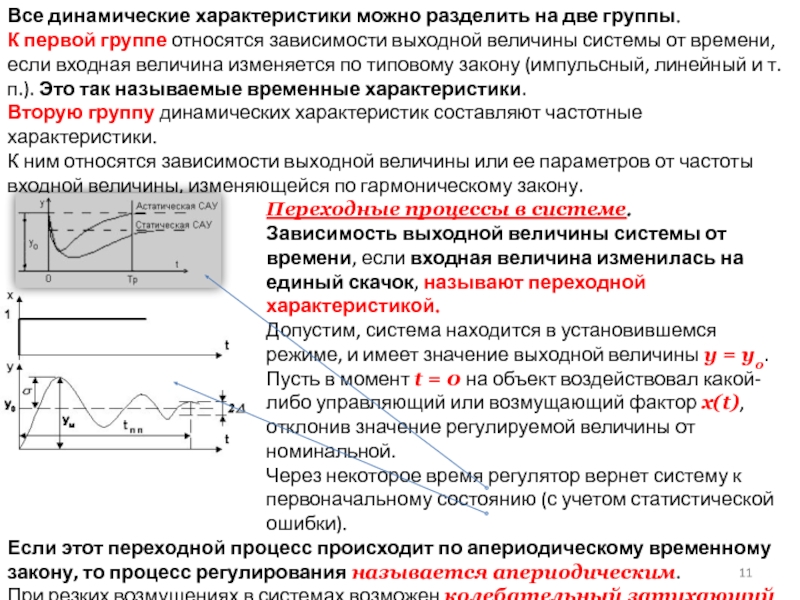
Слайд 12Таким образом, переходная характеристика - это реакция элемента системы на
ступенчатое изменение входной величины, как правило, единичное x(t) = 1(t).
Под входной величиной понимается любой из управляющих или возмущающих воздействий, в многомерных или многоканальных системах – одно из воздействий.
Переходная характеристика может быть задана таблично, графически или аналитически в виде системы уравнений {x = 1(t), y = F(t)}.
Оценки переходных характеристик производятся с помощью следующих показателей:
∎ Характер временной зависимости. По характеру зависимости переходные характеристики делятся на монотонные и колебательные. Переходная характеристика считается монотонной, если она имеет не более одного экстремума. В противном случае переходную характеристику относят к колебательной (немонотонной).
∎ Время переходного процесса – это время, в течение которого выходная величина после начала изменения входной достигает нового установившегося значения. Теоретически это время стремиться к бесконечности, поэтому за время переходного процесса принимают время, за которое выходная величина достигает нового установившегося значения с заданной степенью точности tпп, обычно порядка 3-5% от нового установившегося значения.
Нетрудно заметить, что степень точности D соответствует статической ошибке регулирования.

Слайд 13∎ Динамическая ошибка - это разность между действительным значением выходной
величины yi в данный момент (ti) и её новым установившемся значением y0,
т.е
Dy(t) = y(t) – y0.
Динамическая ошибка представляет собой функцию времени. Максимальную положительную относительную ошибку за время переходного процесса называют выбросом. Выброс определяется формулой:
s = (yм – y0) / y0
∎ Колебательность - количество полных колебаний за время переходного процесса. Колебательность может характеризоваться частотой или периодом колебаний выходной величины.
Импульсная характеристика является другой не менее распространенной временной характеристикой системы.
Её называют импульсной переходной характеристикой или функцией веса и обозначают h(t). Это зависимость выходной величины системы от времени, если входная величина изменилась на единичный идеальный импульс.
Для получения импульсной характеристики используют импульсы прямоугольной формы.
Такой импульс аналитически определяется выражениями:
A(t) = 0, 0 > t >t;
A(t) = a, 0 ≤ t ≤ t ;
A(t) dt = a t .
Слайд 14Произведение at часто называют величиной импульса. Если величина импульса равна
единице, то импульс называют единичным. Если t → 0, то
импульс называет идеальным. Он является теоретической дельта –функцией d(t) с бесконечной амплитудой в точке t=0 и площадью, равной 1.
Импульсная характеристика - это реакция системы на идеальное единичное импульсное изменение входной величины.
Она может быть задана аналитически в виде системы уравнений {x = d(t), y = F(t)}.
Так как идеальный импульс представляет собой производную скачка, d(t) = d [1(t)] / dt, то импульсная характеристика есть производная переходной характеристики системы.
Оценка импульсной характеристики производится теми же показателями, что и переходной.
Пример характеристики приведен на рис.
Слайд 15УРАВНЕНИЯ СОСТОЯНИЯ СИСТЕМ УПРАВЛЕНИЯ
Динамические системы, в которых предполагается, что прохождение
возмущения от входа к выходу в ОУ происходит мгновенно, описываются
обыкновенными дифференциальными уравнениями и называются системами с сосредоточенными параметрами.
Например:
система управления двигателем,
химическим реактором,
самолетом и т.п.
Динамические системы, в которых предполагают, что время прохождения возмущения конечно, описываются дифференциальными уравнениями в частных производных и называются системами с распределенными параметрами.
Например:
прохождение воды в трубопроводе,
распространение тепла в реакторе,
регулирование температуры в нефтепроводе и т.п.
Слайд 16Нормальное уравнение состояния.
Уравнением состояния системы называют равенство, связывающее входные
и выходные величины, изменяющиеся во времени, и справедливое для любого
момента времени.
Известно, что любую величину, изменяющуюся во времени можно представить в виде дифференциального уравнения. Представим в этом виде управляющий сигнал на входе системы:
Соответственно, уравнение сигнала на выходе элемента:
В каждый текущий момент времени система находится в состоянии определенного равновесия между входом и выходом: Y(t) = K U(t), или
Это уравнение называют нормальным уравнением состояния системы. В более общем виде оно записывается в следующей форме :
или с приведением к нормализованной форме
Сопоставлением получаем значения коэффициента усиления K = bm/an, и постоянных времени Ti = an-i/an, tj = bm-j/bm. Коэффициент передачи и постоянные времени однозначно характеризуют свойства системы, в большинстве случаев являются постоянными величинами и называются параметрами системы.
Слайд 17Полное уравнение системы.
Полное поведение системы или любого ее звена
в зависимости от всех воздействующих факторов описывается уравнением временной динамики
y(t) = F(u,f,t).
Как правило, это система дифференциальных уравнений.
Поэтому основным методом исследования систем является метод решения дифференциальных уравнений.
Порядок дифференциальных уравнений может быть довольно высоким, и определенной зависимостью могут быть связаны как входные и выходные величины u(t), f(t), y(t), так и скорости их изменения, ускорения и т.д.
Поэтому уравнение временного состояния системы в общем виде можно записать так:
F(y, y', y'',..., y(n) , u, u', u'',..., u(m) , f, f ', f '',..., f(k)) = 0.
Существует два способа получения дифференциальных уравнений объекта:
Способ применения известных законов (закон Ома, законы механики и т.д.). Способ применим в случаях, когда объект управления простой и система невысокого порядка, или когда объект сложный, но можно воспользоваться законами статистики.
Эвристический способ. Используются уравнения, основанные на опыте работы с предыдущими объектами, экспертные оценки, мнение специалистов. Такое описание называют феноменологическим, т.е. описанием объекта по основным чертам его внешнего поведения, без глубокого формального (математического, физического и т.п.) проникновения в сущность его функционирования.
Для полученной модели должны быть исследованы:
1. Адекватность модели поведению реального объекта;
2. Границы адекватности по пределам изменения параметров и переменных модели.

Слайд 18Линеаризация уравнения динамики.
В общем случае уравнение динамики оказывается нелинейным.
В целях упрощения решений нелинейные уравнения заменяют линейными, которые приблизительно
(с определенной точностью) описывают динамические процессы в системе.
В основе линеаризации нелинейных уравнений лежит допущение:
в нормально функционирующей системе отклонения регулируемой величины и переменных процесса от стационарных (установившихся) значений представляют собой достаточно малые величины. Это положение, как правило, всегда действительно для замкнутых систем.
В пределах малых отклонений нелинейные зависимости между величинами, входящими в уравнение динамики, могут быть приближенно представлены отрезками прямых линий.
Например, нелинейная статическая характеристика звена на участке АВ (рис.) может быть представлена отрезком касательной А"В" в точке номинального режима. Начало координат переносится в точку О', и в уравнениях записываются не абсолютные значения величин y, u, f, а их отклонения от номинальных значений: Dy = y-ун, Du = u-uн, Df = f-fн. Это позволяет получить нулевые начальные условия, если считать, что при t ≤ 0 система находилась в номинальном режиме.

Слайд 19Если допустить, что система находится в номинальной рабочей точке U0'
= uн, У0’ = yн, то ее состояние в установившемся
режиме опишется уравнением статики: Y0’ = K X0’. При выходе из установившегося состояния координаты системы получат приращения и станут равными
U = U0’+DU, Y = Y0’+DY,
а поскольку производные от постоянных величин равны нулю
(di(X0’+DX)/dti = di(DX)/dti),
то уравнение такого состояния будет иметь вид
Для переноса в уравнении начала координат в рабочую точку вычтем из него уравнение статики. В результате получим:
.
Это уравнение обычно называют уравнением состояния системы в приращениях от рабочей точки.
Слайд 20Аналогично можно выполнить и линеаризацию функции нескольких переменных. Для примера
возьмем характерный вариант уравнения динамики систем с ограниченным количеством производных:
F(y,y',y",u,u') = f.
Здесь производные по времени u',y',y" также являются переменными.
В точке, близкой к номинальному режиму: f = fн+Df и F = Fн+DF.
Разложим функцию F в ряд Тейлора в окрестности точки номинального режима и, отбрасывая члены ряда высоких порядков малости, получим:
В номинальном режиме имеем частное решение Fн = fн, а все частные производные функции F в точке O' представляют собой некоторые постоянные коэффициенты, или переменные во времени, если функция F содержит переменную t в явном виде.
Заменяя значения частных производных соответствующими коэффициентами и переходя от приращений переменных к их производным, получаем:
A0 y'' + A1 y' + A2 y = B0 u' + B1 u + f.
В данном уравнении используются не абсолютные значения величин y, u, f и их производных по времени, а отклонения этих величин от номинальных значений (уравнение в отклонениях).
Слайд 21В общем случае частные производные представляют собой:
либо постоянные матрицы
зависимости от внешних воздействий f, значения которых могут быть существенно
нелинейными,
либо матрицы, зависящие только от времени, и полученное уравнение есть
либо система линейных дифференциальных уравнений с постоянными коэффициентами относительно отклонений y и u,
либо система с переменными коэффициентами, которые и решаются относительно выходной величины.
Порядок системы уравнений равен n по порядку производной при y.
Для дифференциального уравнения произвольного порядка:
A0 y(n) + A1 y(n-1) + ... + An-1 y' + An y = B0 u(m) + ... + Bm-1 u' + Bm u + f.
К частным производным линеаризованной системы можно применить принцип суперпозиции:
реакция системы на несколько одновременно действующих входных воздействий равна сумме реакций на каждое воздействие в отдельности.
Это позволяет звено с двумя входами u и f разложить на два звена, каждое из которых имеет один вход и один выход. Поэтому в дальнейшем ограничимся изучением поведения систем и звеньев с одним входом, уравнение динамики которых имеет вид:
a0 y(n) + a1 y(n-1) + ... + an-1 y' + an y = b0 u(m) + ... + bm-1 u' + bm u.
где n ≥ m, так как при n < m системы технически нереализуемы.
Это уравнение описывает систему в динамическом режиме лишь приближенно с той точностью, которую обеспечивает линеаризация.

Слайд 22Передаточная функция.
В теории управления часто используют символическую операторную форму
записи дифференциальных уравнений.
При этом вводится понятие алгебраизированного оператора дифференцирования
p = d/dt
так, что,
dy/dt = py,
а
pn = dn /dtn.
Это лишь другое сокращенное обозначение операции дифференцирования. Соответственно, операция интегрирования записывается как 1/p.
В операторной форме исходное дифференциальное уравнение записывается как алгебраическое:
a0p(n)y+a1p(n-1)y+...+any = (a0p(n)+a1p(n-1)+...+ an)y = (b0p(m)+...+bm-1p+bm)u.
Не надо путать эту форму записи с операционным исчислением.
Здесь используются непосредственно функции y(t), u(t) (оригиналы), а не их изображения Y(p), U(p), получаемые из оригиналов преобразованием Лапласа.
При нулевых начальных условиях с точностью до обозначений записи действительно похожи, и некоторые правила операционного исчисления применимы к операторной форме записи уравнений динамики.
Так, оператор р можно выносить за скобки и можно рассматривать в качестве сомножителя, но без права перестановки: py ≠ yp.
Условно можно считать оператор р алгебраической величиной.

Слайд 23Уравнение динамики в операторной форме:
Дифференциальный оператор W(p) называют передаточной функцией.
Она определяет зависимость отношения выходной величины звена к входной во
времени: W(p) = y(p)/u(p), т.е. динамический коэффициент усиления.
Передаточные функции в операторной форме также представляют собой сокращенную символическую запись дифференциальных уравнений.
В установившемся режиме d/dt = 0, p = 0, и передаточная функция превращается в коэффициент передачи звена K = bm /an.
Знаменатель передаточной функции D(p) = a0pn+a1pn-1+a2pn -2+...+an называют характеристическим полиномом.
Его корни, при которых знаменатель D(p) обращается в ноль, а W(p) стремится к бесконечности, называются полюсами передаточной функцией.
Числитель K(p) = b0pm+b1pm-1+...+bm называют операторным коэффициентом передачи.
Его корни, при K(p) = 0 и W(p) = 0, называются нулями передаточной функции.
Слайд 24Звено системы с известной передаточной функцией называют динамическим звеном.
Под
динамическим звеном понимают устройство любого физического вида и конструктивного оформления,
описываемое определенным дифференциальным уравнением.
На схемах динамическое звено изображают прямоугольником, внутри которого записывается выражение передаточной функции.
Для звена с двумя входами и одним выходом (рис.) должны быть записаны передаточные функции по каждому из входов.
Передаточная функция является основной характеристикой звена, из которой можно получить все остальные характеристики.
Она определяется только параметрами системы и не зависит от входных и выходных величин.
Например, одним из динамических звеньев является интегратор.
Его передаточная функция Wи(p) = 1/p.
Схема системы, составленная из динамических звеньев, называется структурной.
Слайд 25Элементарные динамические звенья.
Динамика большинства функциональных элементов систем независимо от
исполнения может быть описана одинаковыми по форме дифференциальными уравнениями не
более второго порядка. Такие элементы называют элементарными динамическими звеньями. Элементарные динамические звенья имеют один вход и один выход, а передаточная функция элементарного звена задается отношением двух полиномов:
Wэ(p) = (b0p2 + b1p + b2) / (a0p2 + a1p + a2).
Известно также, что любой полином произвольного порядка можно разложить на простые сомножители:
D(p) = a0p(n) + a1p(n-1) +...+an = a0 (p-p1) (p-p2)...(p-pn),
где p1, p2, ... , pn - корни полинома D(p). Аналогично:
K(p) = b0p(m)+...+ bm-1p+bm = b0 (p-p~1) (p-p~2)...(p-p~m),
где p~1, p~2, ... , p~m - нули полинома K(p). Отсюда:
Корни любого полинома могут быть либо вещественными, либо комплексными попарно сопряженными. Пара комплексно сопряженных корней соответствует полиному второй степени. Передаточную функцию линеаризованной системы можно представить как произведение передаточных функций элементарных звеньев:
W = K W1 W2 W3 … ,
где К=b0/a0 – множитель, которым может регулироваться общая чувствительность системы к управляющим или дестабилизирующим воздействиям.

Слайд 26Каждому такому звену в системе, как правило, соответствует отдельный узел.
Зная свойства отдельных звеньев можно судить о динамике системы в
целом.
Классификация звеньев производится по виду их дифференциальных уравнений и соответствующих передаточных функций, независимо от исполнения (механические, гидравлические, электрические и пр.).
Передаточные функции типовых звеньев, из которых синтезируются системы, обычно имеют числитель или знаменатель, равный единице.
СТРУКТУРНЫЕ СХЕМЫ СИСТЕМ УПРАВЛЕНИЯ
Преобразования структурных схем.
Структурная схема системы в простейшем случае строится из элементарных динамических звеньев. Несколько элементарных звеньев могут быть заменены одним звеном со сложной передаточной функцией. Для этого существуют правила эквивалентного преобразования структурных схем.
Последовательное соединение (рис. 2.5.1) - выходная величина предшествующего звена подается на вход последующего.
При этом можно записать:
y1 = W1 y0; y2 = W2 y1; ... ; yn = Wn yn-1,
yn = W1 W2 ...Wn y0 = Wэкв y0.
Wэкв = Wi.
Передаточные функции последовательно соединенных звеньев перемножаются.

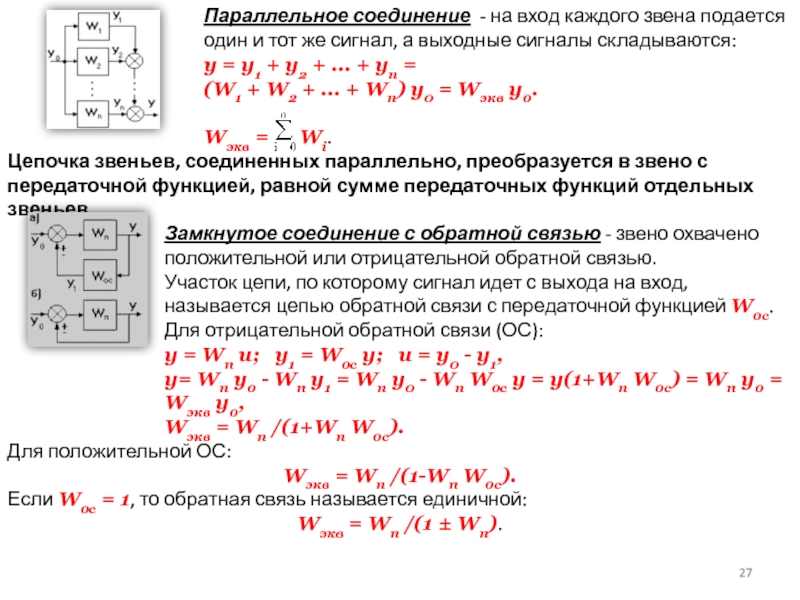
Слайд 27Параллельное соединение - на вход каждого звена подается один и
тот же сигнал, а выходные сигналы складываются:
y = y1 +
y2 + ... + yn =
(W1 + W2 + ... + Wn) y0 = Wэкв y0.
Wэкв = Wi.
Цепочка звеньев, соединенных параллельно, преобразуется в звено с передаточной функцией, равной сумме передаточных функций отдельных звеньев.
Замкнутое соединение с обратной связью - звено охвачено положительной или отрицательной обратной связью.
Участок цепи, по которому сигнал идет с выхода на вход, называется цепью обратной связи с передаточной функцией Wос.
Для отрицательной обратной связи (ОС):
y = Wп u; y1 = Wос y; u = y0 - y1,
y= Wп y0 - Wп y1 = Wп y0 - Wп Woc y = y(1+Wп Woc) = Wп y0 = Wэкв y0,
Wэкв = Wп /(1+Wп Wос).
Для положительной ОС:
Wэкв = Wп /(1-Wп Wос).
Если Woc = 1, то обратная связь называется единичной:
Wэкв = Wп /(1 ± Wп).
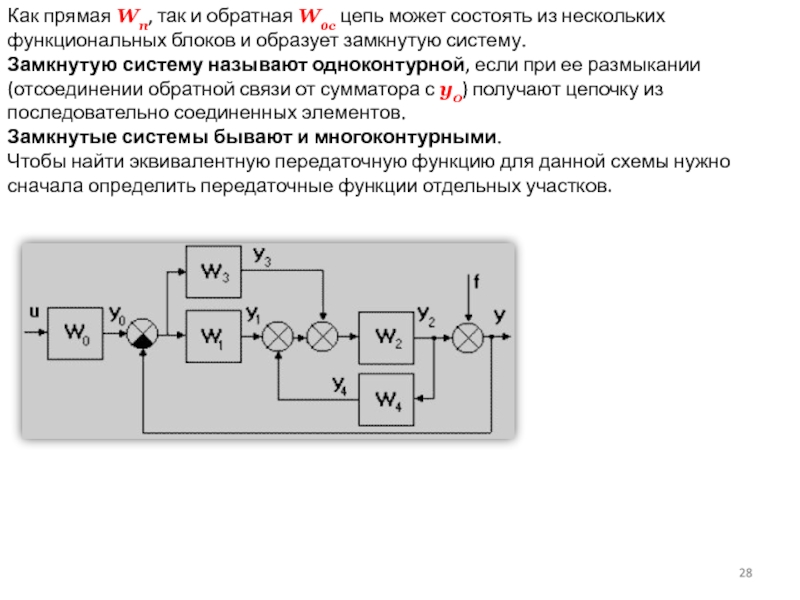
Слайд 28Как прямая Wп, так и обратная Wос цепь может состоять
из нескольких функциональных блоков и образует замкнутую систему.
Замкнутую систему
называют одноконтурной, если при ее размыкании (отсоединении обратной связи от сумматора с y0) получают цепочку из последовательно соединенных элементов.
Замкнутые системы бывают и многоконтурными.
Чтобы найти эквивалентную передаточную функцию для данной схемы нужно сначала определить передаточные функции отдельных участков.
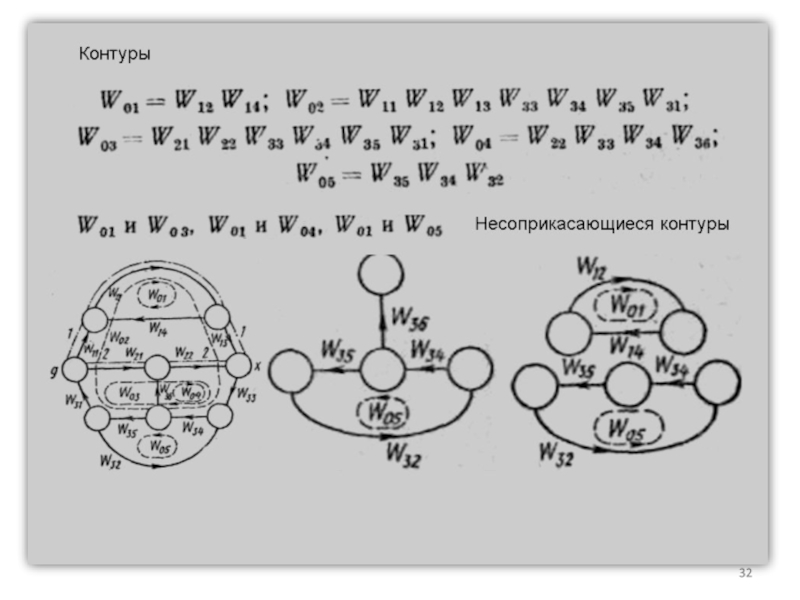
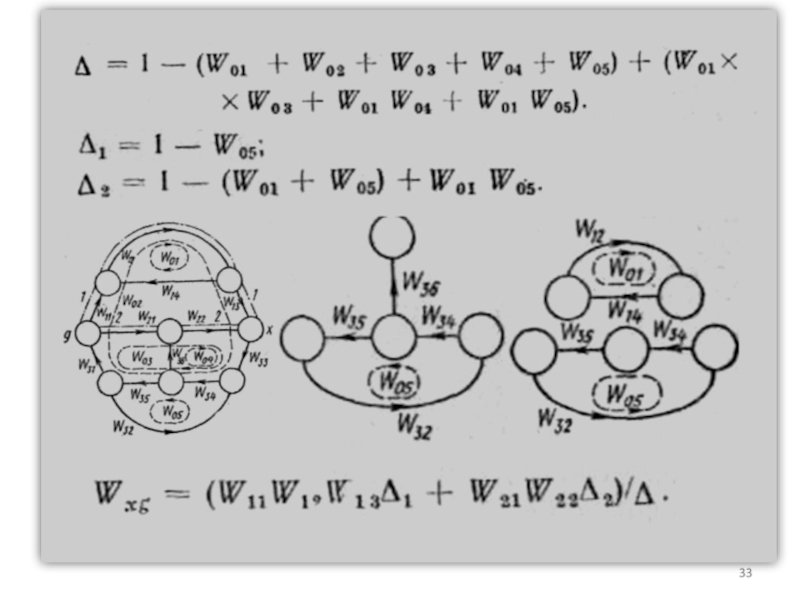
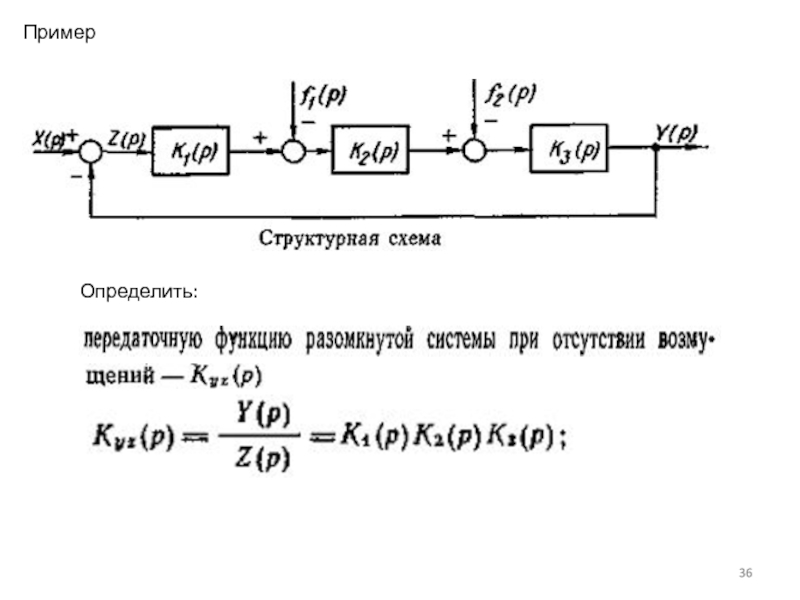
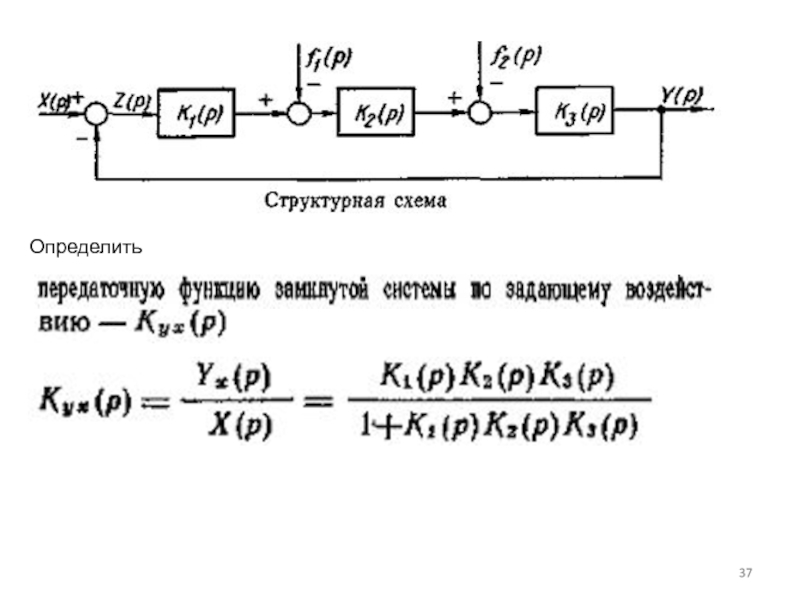
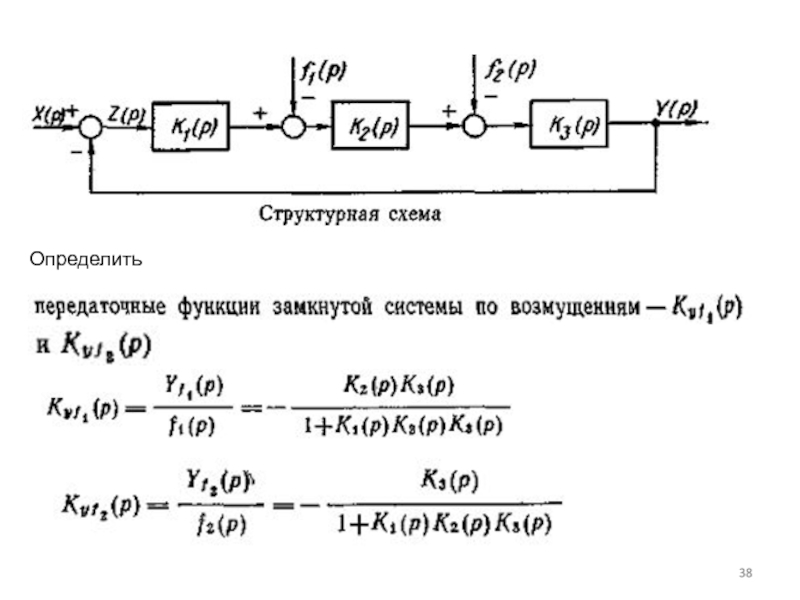
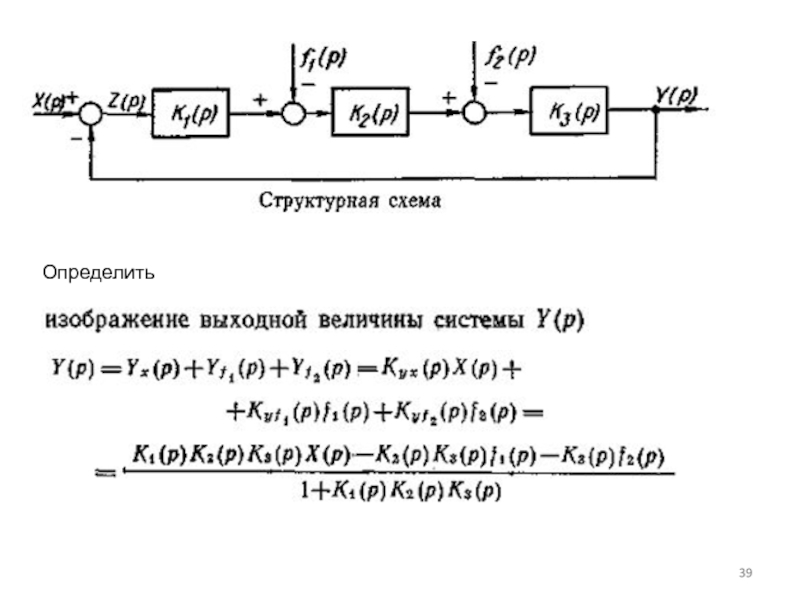
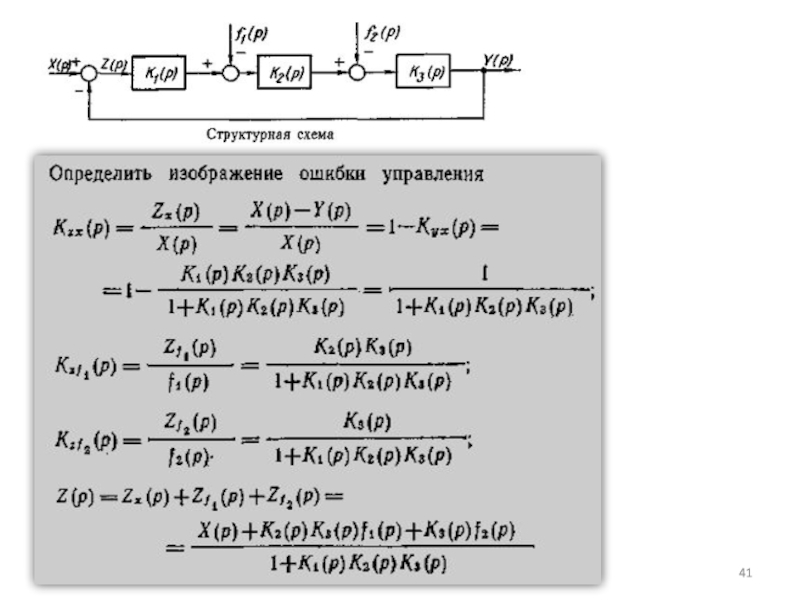
Слайд 34Определение передаточных функций разомкнутых и замкнутых систем