Слайд 1Статические массивы
Понятие
Заполнение значениями;
Вычисления;
Поиск;
Вычислительная сложность алгоритмов;
Сортировка.
Слайд 2Статические массивы
1. Понятие
Массивы – формальное объединение нескольких однотипных объектов (чисел,
символов, строк и т.п.), рассматриваемое как единое целое.
var
a: array
[1..10] of real;
b: array[0..50] of integer;
c: array[-3..4] of boolean;
Объявление массива
b[17] := 123;
c[-2] := a[1]>a[2];
for k := 1 to 10 do a[k] := 0;
Обращение к элементу массива
Слайд 3Статические массивы
Статические массивы
var
a: array[1..3] of array[–2..2] of array[1..5] of
real;
var
a: array[1..3, –2..2, 1..5] of real;
или более компактная запись
Многомерные
массивы
Слайд 4Статические массивы
Статические массивы
var
a, b: Vector;
или
a, b: array[1..5]
of real;
...
a := b;
Можно передать все элементы одного массива другому
массиву
var
a: array[1..5] of real;
b: array[1..5] of real;
...
a := b; {Здесь возникнет ошибка несоответствия типов}
Слайд 5Статические массивы
Статические массивы
var
a, b: array[1..5] of real;
eq: boolean;
i: integer;
...
eq := true;
for i := 1 to 5 do
if a[i]<>b[i] then eq := false;
if eq then ...
Над массивами не определены операторы отношения
Слайд 6Статические массивы
Понятие
Заполнение значениями;
Вычисления;
Поиск;
Вычислительная сложность алгоритмов;
Сортировка.
Слайд 7Генератор случайного числа:
Random(maxValue: integer): integer;
Возвращает случайное целое в
диапазоне от 0 до maxValue-1
Random(a,b: integer): integer;
Возвращает случайное
целое в диапазоне от a до b
Random: real;
Возвращает случайное вещественное в диапазоне [0..1)
Пример: заполнить массив вещественными числами из отрезка [5;10]
2. Заполнение значениями
2. Заполнение значениями
Слайд 8const
N = 10;
var
m : array [1..N] of real;
// массив
i : integer;
// счетчик цикла
begin
// заполнение массива значениями
for i := 1 to N do
m[i] := random(50+1)/10 + 5;
// вывод значений на экран
for i := 1 to N do
writeln('m[',i:2,'] =',m[i]:4:1);
end.
Вариант 1 (используя Random(maxValue: integer): integer)
m[ 1] = 9.1
m[ 2] = 9.9
m[ 3] = 6.0
m[ 4] = 5.7
m[ 5] = 7.3
m[ 6] = 5.0
m[ 7] = 9.0
m[ 8] = 9.4
m[ 9] = 5.9
m[10] = 7.0
2. Заполнение значениями
Статические массивы
Слайд 9const
N = 10;
var
m : array [1..N] of real;
// массив
i : integer;
// счетчик цикла
begin
// заполнение массива значениями
for i := 1 to N do
m[i] := random(50,100)/10;
// вывод значений на экран
for i := 1 to N do
writeln('m[',i:2,'] =',m[i]:4:1);
end.
Вариант 2 (используя Random(a,b: integer): integer)
m[ 1] = 7.2
m[ 2] = 6.4
m[ 3] = 5.0
m[ 4] = 5.0
m[ 5] = 6.2
m[ 6] = 5.9
m[ 7] = 8.5
m[ 8] = 7.9
m[ 9] = 7.1
m[10] = 9.5
2. Заполнение значениями
Статические массивы
Слайд 10const
N = 10;
var
m : array [1..N] of real;
// массив
i : integer;
// счетчик цикла
begin
// заполнение массива значениями
for i := 1 to N do
m[i] := random*5 + 5;
// вывод значений на экран
for i := 1 to N do
writeln('m[',i:2,'] =',m[i]:4:1);
end.
Вариант 3 (используя Random: real)
m[ 1] = 6.0
m[ 2] = 5.9
m[ 3] = 5.5
m[ 4] = 6.1
m[ 5] = 7.7
m[ 6] = 9.3
m[ 7] = 9.6
m[ 8] = 9.0
m[ 9] = 7.4
m[10] = 5.2
2. Заполнение значениями
Статические массивы
Слайд 11Замечания по примеру:
в данном случае можно было использовать только
один цикл, в нем формировать и выводить на экран значения.
В общем случае на операции формирования, обработки и вывода требуется свой цикл;
в вариантах 1 и 2 результат вещественный с точностью до десятых, в 3 – 11-12 значимых.
2. Заполнение значениями
2. Заполнение значениями
Слайд 12Пример: заполнение двумерного массива
2. Заполнение значениями
2. Заполнение значениями
const
Nr = 2; Nc = 4;
var
a, b
: array [1..Nr,1..Nc] of integer;
i,j : integer;
begin
writeln('После объявления массива a');
for i := 1 to Nr do
begin
for j := 1 to Nc do write (a[i,j]:3);
writeln;
end;
for i := 1 to Nr do
for j := 1 to Nc do a[i,j] := random(11);
Слайд 13 2. Заполнение значениями
2. Заполнение значениями
writeln('После заполнения массива a');
for
i := 1 to Nr do
begin
for j
:= 1 to Nc do write (a[i,j]:3);
writeln;
end;
b := a;
writeln('Содержимое массива b');
for i := 1 to Nr do
begin
for j := 1 to Nc do write (b[i,j]:3);
writeln;
end;
end.
После объявления массива a
0 0 0 0
0 0 0 0
После заполнения массива a
0 9 1 4
2 7 5 5
Содержимое массива b
0 9 1 4
2 7 5 5
Слайд 14Статические массивы
Понятие
Заполнение значениями;
Вычисления;
Поиск;
Вычислительная сложность алгоритмов;
Сортировка.
Слайд 15Задача вычисления:
среднее арифметическое;
среднее геометрическое;
аппроксимация;
интерполяция;
и другие
математические вычисления
3. Вычисления
3. Вычисления
Слайд 16Аппроксимация – приближенное описание сложной функции более простыми
3. Вычисления
3.
Вычисления
Слайд 17Интерполяция - нахождения промежуточных значений величины по имеющемуся дискретному набору
известных значений
3. Вычисления
3. Вычисления
Слайд 183. Вычисления
3. Вычисления
Алгоритм решения:
Задать значения функции в виде точек
(массив аргументов, массив значений)
Задать точку, для которой вычисляется значение функции.
Найти
в массиве аргументов ближайший к заданной точке.
Вычисление коэффициентов полинома первого порядка (y=kx+b)
Вычисление значения функции в заданной точке.
Пример: вычислить значение функции в точке заданной таблично
Слайд 193. Вычисления
2. Вычисления
const
N = 5;
var
mx : array
[1..N] of real; // массив аргументов
my : array
[1..N] of real; // массив значений
x,y : real; // точка, для которой вычисляется
k,b : real; // коэффициенты полинома
i : integer; // счетчик цикла
findPoint: boolean; // маркер поиска точки
Слайд 203. Вычисления
2. Вычисления
begin
writeln('Задайте функцию в виде таблицы');
for
i := 1 to N do
begin
write('Точка ',i,' (x,y) ');
read(mx[i], my[i]);
end;
write('Введите значение аргумента, для которого необходимо вычислить значение функции, x=');
readln(x);
Слайд 213. Вычисления
3. Вычисления
//поиск ближайшего аргумента
i := 1; findPoint
:= false;
while not findPoint do // поиск ближайшего
аргумента
begin
if (x >= mx[i]) and (x < mx[i+1]) then
begin // ближайший аргумент найден
findPoint := true;
k := (my[i+1] - my[i])/(mx[i+1] - mx[i]);
b := my[i] - k*mx[i];
y := k*x+b;
writeln('Значение функции в точке x=',x,' равно y=',y:0:2);
end;
if i = N-1 then // точки кончились
findPoint := true;
else
i := i + 1;
end;
end.
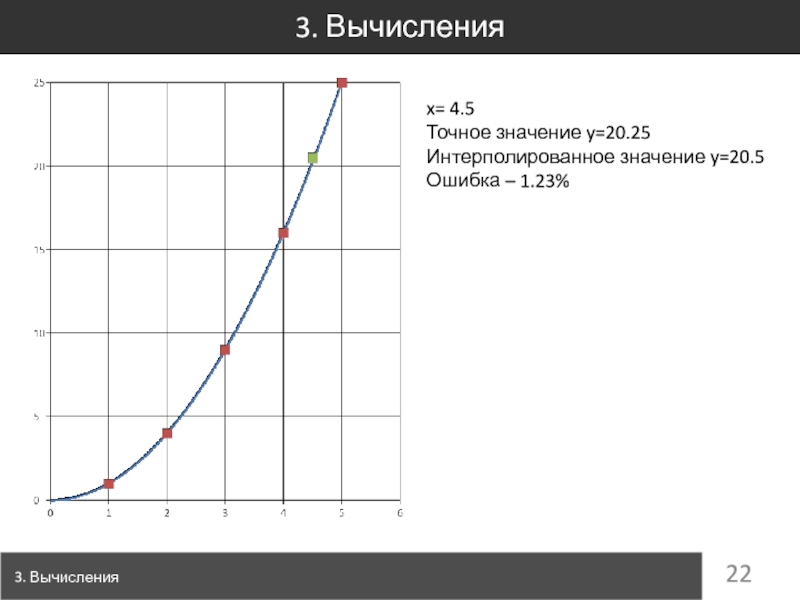
Слайд 223. Вычисления
3. Вычисления
x= 4.5
Точное значение y=20.25
Интерполированное значение y=20.5
Ошибка –
1.23%
Слайд 23Статические массивы
Понятие
Заполнение значениями;
Вычисления;
Поиск;
Вычислительная сложность алгоритмов;
Сортировка.
Слайд 244. Поиск
4. Поиск
поиск min/max
поиск по заданному условию
поиск цепочек
Слайд 254. Поиск
4. Поиск
Алгоритм решения:
Заполнить массив случайными числами
Поиск подряд идущих
четных элементов
Определение самой длинной из них
Пример: Найти и вывести самую
длинную цепочку четных элементов массива
Слайд 264. Поиск
4. Поиск
const
N = 20;
var
m : array
[1..N] of integer;
i : integer;
c, l :
integer; //позиции и длина текущей цепочки
cm, lm : integer; //позиции и длина самой длинной цепочки
flag1, flag2 : boolean; // флаги цепочки
begin
for i := 1 to N do
begin //заполним и распечатаем массив
m[i] := random(10 + 1);
write(m[i],' ');
end; П
Writeln;
Слайд 274. Поиск
3. Поиск
// зададим начальные значения для текущий
//
позиций цепочки и их макс знач.
c := 0; l
:= 0;
cm := 0; lm := 0;
flag1 := false; flag2 := false;
for i := 2 to N do
begin
flag2 := (m[i-1] mod 2=0) and (m[i] mod 2=0); // два соседних элемента четные
if flag2 then
begin
if not flag1 then begin c := i-1; l := 2; end //два подряд четных, а пред - нет
else l := i - c + 1; //больше двух подряд четных
if l > lm // длина текущей цепочки больше предыдущей
then cm := c; lm := l;
end
else
begin
// сброс параметров текущей цепи в нуль
l := 0; c := 0;
end;
flag1 := flag2;
writeln(c,'-',l,'|',cm,'-',lm);
end;
Слайд 28Статические массивы
3. Поиск
if cm 0 then
for i := cm to cm+lm-1 do write(m[i],' ')
else writeln('Цепочек нет')
end.
Слайд 294. Поиск
3. Поиск
Алгоритм решения:
Заполнить массивы координатами точек
Задать координаты заданной
точки
Обойти все исходные точки, определить расстояние до каждой их них
Запомнить
минимальное расстояние
Пример: Найти точку на плоскости, ближайшую заданной
Слайд 304. Поиск
3. Поиск
const
N = 5; //кол-во точек
на плоскости
var
px,py : array [1..N] of real; // координаты
исходных точек
x,y : real;
i, imin : integer;
L, Lmin : real; //текущее и минимальное расстояние
begin
writeln('Исходные точки');
for i := 1 to N do // заполняем координаты точек
begin
px[i] := 5 - 10*random;
py[i] := 5 - 10*random;
writeln('(',px[i]:5:2,',',py[i]:5:2,')');
end;
writeln('Введите координаты точек');
write('x=');readln(x);
write('y=');readln(y);
Слайд 314. Поиск
3. Поиск
Lmin := sqrt(sqr(x-px[1]) + sqr(y-py[1]));
imin := 1;
writeln('Точка #1 расстояние ',Lmin:5:2);
for i :=
2 to N do
begin
L := sqrt(sqr(x-px[i]) + sqr(y-py[i]));
if Lmin > L then begin Lmin := L; imin := i; end;
writeln('Точка #',i,' расстояние ',L:5:2);
end;
writeln('Ближайшая точка #',imin,' расстояние ',Lmin:5:2);
end.
Слайд 324. Поиск
3. Поиск
(-4.07,-0.33)
( 1.92, 2.72)
(-3.72, 4.01)
(-4.19,-4.36)
(-1.67, 2.33)
Введите координаты точек
x=0
y=0
Точка
#1 расстояние 4.08
Точка #2 расстояние 3.33
Точка #3 расстояние 5.47
Точка #4
расстояние 6.05
Точка #5 расстояние 2.87
Наиближайшая точка #5 расстояние 2.87
Слайд 334. Поиск
Понятие
Заполнение значениями;
Вычисления;
Поиск;
Вычислительная сложность алгоритмов;
Сортировка.
Слайд 345. Вычислительная сложность
5. Вычислительная сложность алгоритма
Вычислительная сложность алгоритма —
это оценка количества операций, требуемых для достижения результата, в зависимости
от количества обрабатываемых элементов.
O(…) – вычислительная сложность «О-большое», значит не хуже чем …
Примеры:
O(1) – операция взятия значения по индексу
O(n) – поиск в массиве конкретного значения методом последовательного перебора
O(logN) – бинарный поиск
O(N^2) – поиск пары самых близко расположенных точек на плоскости
O(2^N), O(N!) – unreal
Слайд 355. Вычислительная сложность
5. Вычислительная сложность алгоритма
Слайд 365. Вычислительная сложность
5. Вычислительная сложность алгоритма
Время вычисления при млн.
операций в секунду
Слайд 375. Вычислительная сложность
5. Вычислительная сложность алгоритма
Какова верхняя оценка O
алгоритма поиска минимального числа?
начало; поиск минимального элемента массива array из
N элементов
min := array[1]
для i от 2 до N выполнять:
если array[i] < min
min := array[i]
конец; вернуть min
N – 1 операция присваивания счетчику цикла i нового значения;
N – 1 операция сравнения счетчика со значением N;
N – 1 операция сравнения элемента массива со значением min;
от 1 до N операций присваивания значения переменной min.
O(f(N)) = O(N-1+N-1+N-1+N +1) = O(4N-2) = O(N)
Слайд 385. Вычислительная сложность
5. Вычислительная сложность алгоритма
Обработка массива размером N=108
Слайд 39Статические массивы
Понятие
Заполнение значениями;
Вычисления;
Поиск;
Вычислительная сложность алгоритмов;
Сортировка.
Слайд 40Задача сортировки:
для заданной последовательности
a1, a2, …, an
найти перестановку её элементов
в таком порядке
a'1,a'2, … ,a'n,
что при заданной функции f справедливо
отношение:
f(a'1) f(a'2) … f(a'n)
f(x) – функция упорядочивания, её значение называется ключом
Типы сортировки:
внутренний (все элементы находятся в памяти машины);
внешний (часть в памяти, часть на внешних носителях);
устойчивая сортировка (не меняет относительный порядок сортируемых элементов, имеющих одинаковые ключи)
Основные характеристики:
время;
дополнительный объем памяти (без привлечения, с привлечением, необходимо копировать массив).
6. Сортировка
6. Сортировка
Слайд 41Сортировка простыми обменами (пузырьком)
564 41 165 815 685 764 827
41 564 165 685 815 764 827
41 165 564
685 764 815 827
41 165 564 685 764 815 827
41 165 564 685 764 815 827
41 165 564 685 764 815 827
41 165 564 685 764 815 827
6. Сортировка
5. Сортировка
Слайд 426. Сортировка
5. Сортировка
const
N = 10;
var
arr:
array[1..N] of integer;
i, j, k: integer;
begin
write ('Исходный массив: ');
for i := 1 to N do begin
arr[i] := random(101);
write (arr[i]:4);
end;
writeln; writeln;
for i := 1 to N-1 do
for j := 1 to N-i do
if arr[j] > arr[j+1] then begin
k := arr[j];
arr[j] := arr[j+1];
arr[j+1] := k
end;
write ('Отсортированный массив: ');
for i := 1 to N do write (arr[i]:4);
writeln;
end.
Слайд 43Сортировка выбором
1) поиск номера минимального значения в текущем списке;
2) обмен
этого значения со значением первой не отсортированной позиции 3) сортируется
хвост списка, исключив из рассмотрения уже отсортированные элементы
195 700 949 274 444 108 698
108 700 949 274 444 195 698
108 195 949 274 444 700 698
108 195 274 949 444 700 698
108 195 274 444 949 700 698
108 195 274 444 698 700 949
108 195 274 444 698 700 949
6. Сортировка
5. Сортировка
Слайд 44Сортировка вставками
10 3 335 33 355 217 536
3 10
335 33 355 217 536
3 10 335 33 355
217 536
3 10 33 335 355 217 536
3 10 33 335 355 217 536
3 10 33 217 335 355 536
3 10 33 217 335 355 536
6. Сортировка
6. Сортировка
Слайд 45Другие методы:
шейкер-сортировка;
метод Шелла;
быстрая сортировка Хора;
быстрая сортировка
(quicksort);
и тд
6. Сортировка
5. Сортировка


![Статические массивы Статические массивыСтатические массивыvar a: array[1..3] of array[–2..2] of array[1..5] of real;var Статические массивыСтатические массивыvar a: array[1..3] of array[–2..2] of array[1..5] of real;var a: array[1..3, –2..2, 1..5] of real;или](/img/thumbs/dd99950cd1e9902397332b1ac70f8cf7-800x.jpg)
![Статические массивы Статические массивыСтатические массивыvar a, b: Vector;или a, b: array[1..5] of real;...a Статические массивыСтатические массивыvar a, b: Vector;или a, b: array[1..5] of real;...a := b;Можно передать все элементы](/img/thumbs/5f53cbdfb9038b8559ba88b960eeb808-800x.jpg)
![Статические массивы Статические массивыСтатические массивыvar a, b: array[1..5] of real; eq: boolean; i: Статические массивыСтатические массивыvar a, b: array[1..5] of real; eq: boolean; i: integer;...eq := true;for i := 1](/img/thumbs/bddf8cfec42985b920612cce9d09bcb8-800x.jpg)


![Статические массивы const N = 10;var m : array [1..N] of real; // const N = 10;var m : array [1..N] of real; // массив i : integer;](/img/thumbs/59e82c7516ffc842bd2c1edb621736b8-800x.jpg)
![Статические массивы const N = 10;var m : array [1..N] of real; // const N = 10;var m : array [1..N] of real; // массив i : integer;](/img/thumbs/a4d681dcc7ae3b6e4518a37e67086d09-800x.jpg)
![Статические массивы const N = 10;var m : array [1..N] of real; // const N = 10;var m : array [1..N] of real; // массив i : integer;](/img/thumbs/f4448cdb18ca788893ce0191940e3047-800x.jpg)








![Статические массивы 3. Вычисления 2. Вычисленияconst N = 5;var mx : array [1..N] 3. Вычисления 2. Вычисленияconst N = 5;var mx : array [1..N] of real; // массив аргументов](/img/thumbs/eed9dc1db03884c71692b0869cb05837-800x.jpg)





![Статические массивы 4. Поиск 4. Поискconst N = 20;var m : array [1..N] 4. Поиск 4. Поискconst N = 20;var m : array [1..N] of integer; i : integer;](/img/thumbs/d038fb5454af8f0fcfbd422ced2aaf4b-800x.jpg)

![Статические массивы Статические массивы 3. Поискif cm 0 then for i := Статические массивы 3. Поискif cm 0 then for i := cm to cm+lm-1 do write(m[i],'](/img/thumbs/d1f6a9576418c85077ac68c0ae44b2bd-800x.jpg)

![Статические массивы 4. Поиск 3. Поискconst N = 5; //кол-во точек на плоскостиvar 4. Поиск 3. Поискconst N = 5; //кол-во точек на плоскостиvar px,py : array [1..N] of](/img/thumbs/7784477b3e148af1f2530e0db2fa450d-800x.jpg)
![Статические массивы 4. Поиск 3. Поиск Lmin := sqrt(sqr(x-px[1]) + sqr(y-py[1])); imin := 4. Поиск 3. Поиск Lmin := sqrt(sqr(x-px[1]) + sqr(y-py[1])); imin := 1; writeln('Точка #1 расстояние ',Lmin:5:2);](/img/thumbs/e4a3efccffde0d4d322190f83bc1b8d7-800x.jpg)










![Статические массивы 6. Сортировка 5. Сортировкаconst N = 10;var arr: array[1..N] of integer; 6. Сортировка 5. Сортировкаconst N = 10;var arr: array[1..N] of integer; i, j, k:](/img/thumbs/45c3a351347bd36a99885cffba8052f2-800x.jpg)