величины, а значения этих пара-метров, измеренные в конкретных опытах —
как реализации случайных величинСлучайные величины бывают дискретными и непрерывными
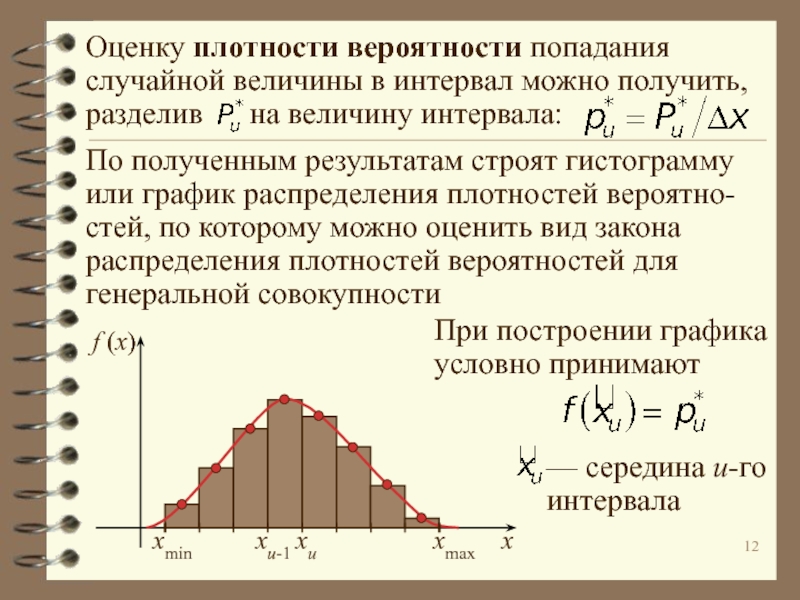
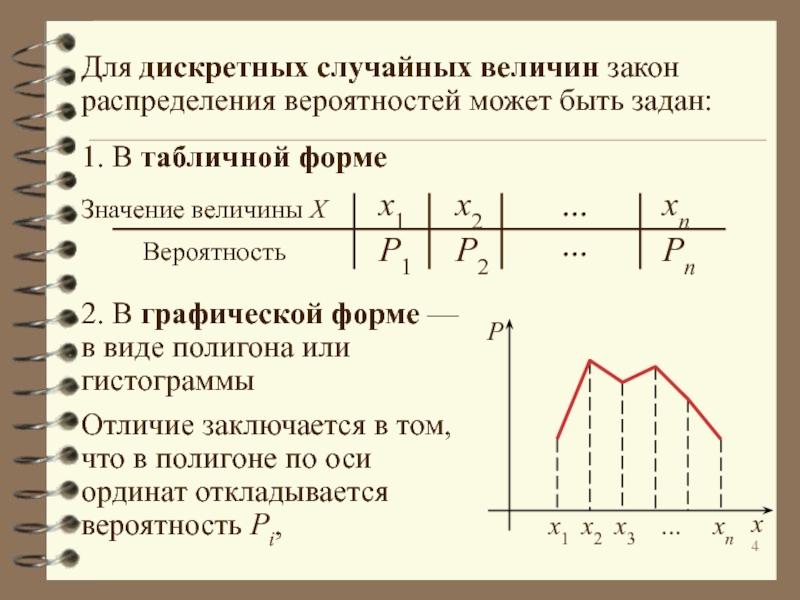
Дискретные величины способны принимать лишь ограниченное число значений, известных заранее, например количество успешных опытов или каких-либо объектов, выражаемое целым числом, лежащем в заданном интервале.
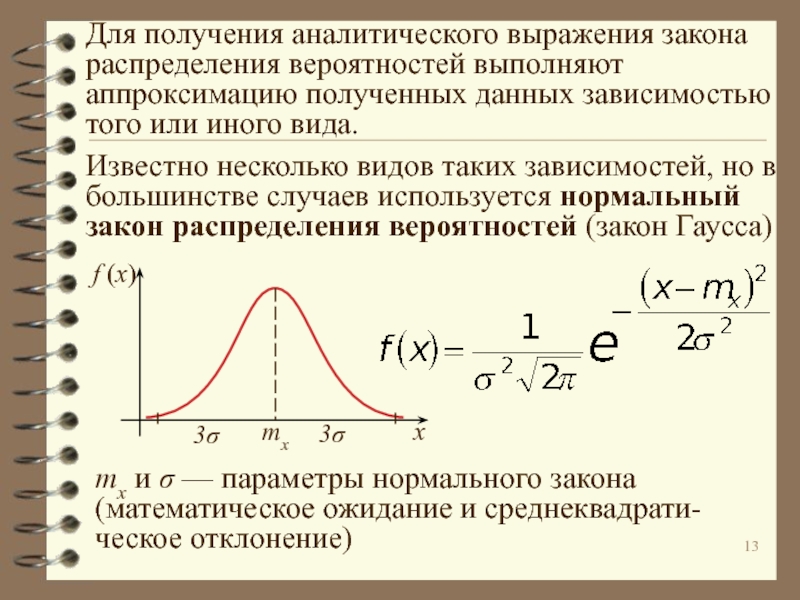
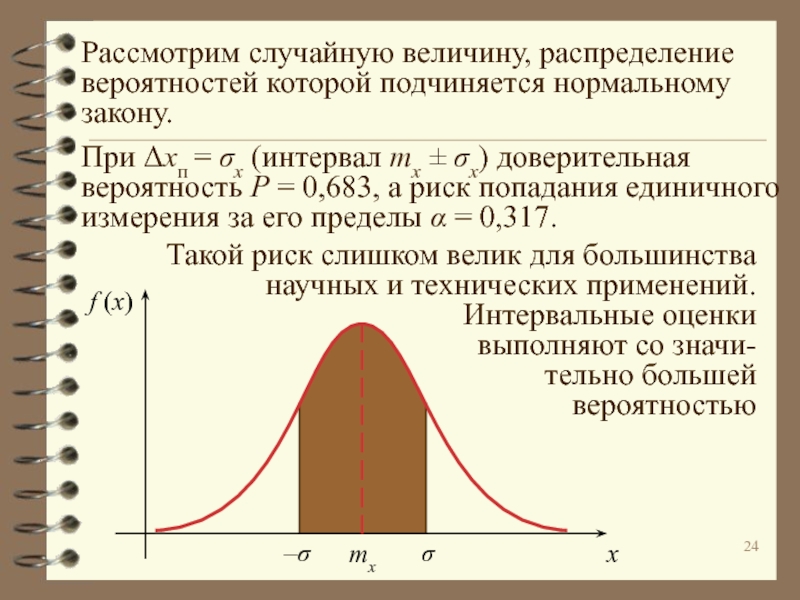
Непрерывные величины могут принимать любое значение в некотором интервале



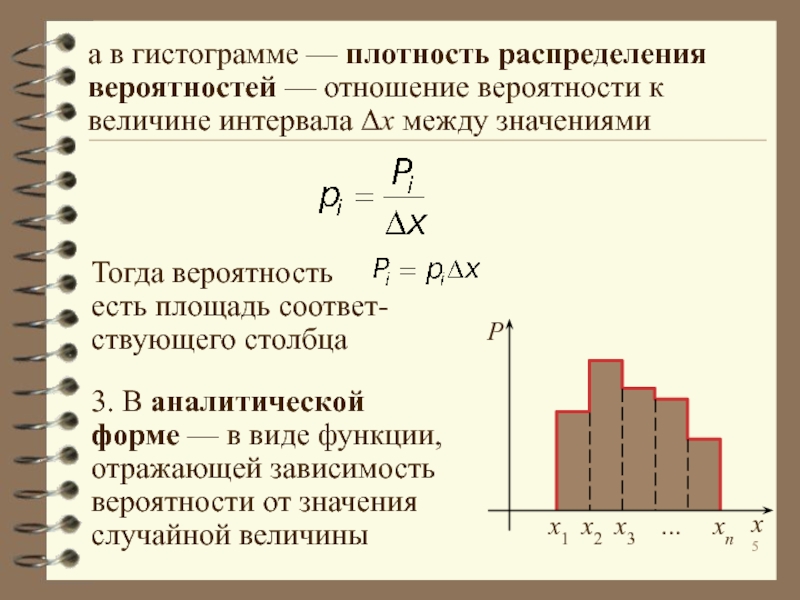
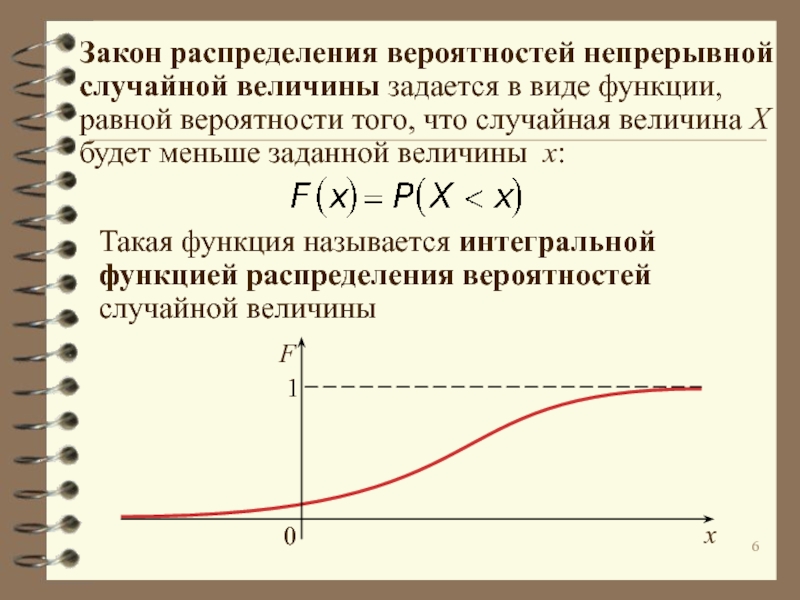
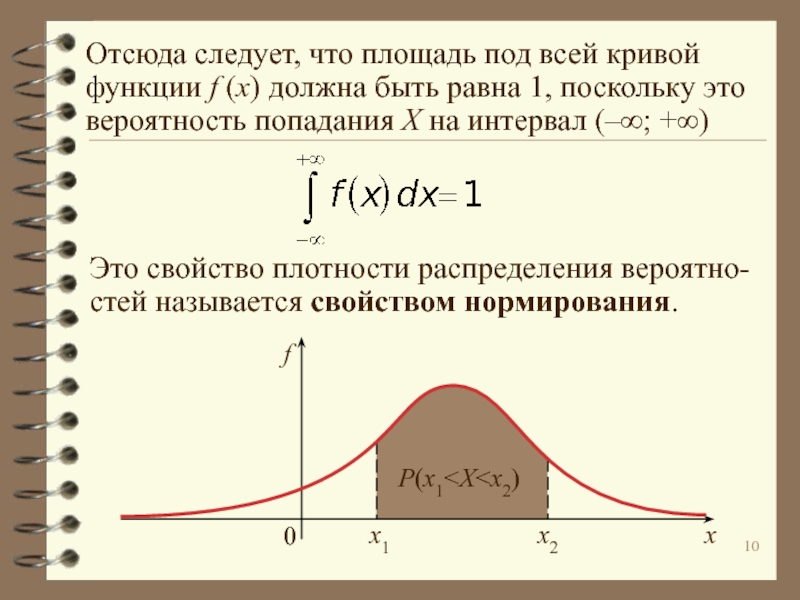
![Статистическая обработка экспериментальных данных Интегральная функция распределения вероятностей позволяет определить вероятность попадания значения случайной величины Интегральная функция распределения вероятностей позволяет определить вероятность попадания значения случайной величины на некоторый интервал [x1; x2]:Эта функция неубывающая;](/img/thumbs/eeb1e6b036dcbaea0d801477437b0b56-800x.jpg)
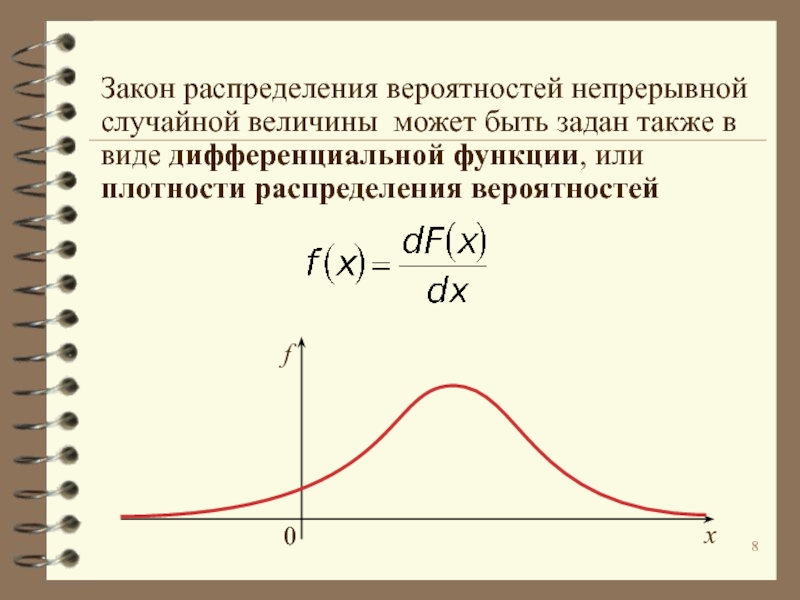
![Статистическая обработка экспериментальных данных Вероятность попадания значения случайной величины на интервал [x1; x2] равна площади фигуры Вероятность попадания значения случайной величины на интервал [x1; x2] равна площади фигуры под графиком функции f(x) на этом](/img/thumbs/32a251eca34bacb7ee1b31b8c28ba05c-800x.jpg)