Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Статистическая теория погрешностей измерения
Содержание
- 1. Статистическая теория погрешностей измерения
- 2. СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯЛекция 2. Статистическая теория
- 3. План лекции1 Классификация погрешностей2 Методы описания случайных
- 4. План лекции10 Определение доверительного значения погрешности результата
- 5. Погрешности измеренийПри любой степени совершенства измерительной аппаратуры,
- 6. Погрешности измеренийАбсолютная погрешность измерений:Относительная погрешность измерений:С учетом
- 7. Классификация погрешностей1. По слагаемым измеренияпогрешность преобразования;погрешность меры;погрешность
- 8. Классификация погрешностей2. По источнику возникновения погрешностиметодическая –
- 9. Классификация погрешностей3. По условиям проведения измеренийосновная погрешность
- 10. Классификация погрешностей4. По способу выражения погрешностиабсолютная погрешность
- 11. Классификация погрешностейКласс точностиКласс точности измерительного прибора –
- 12. Классификация погрешностей5. По способу взаимодействия со значением
- 13. Классификация погрешностей5. По способу взаимодействия со значением
- 14. Классификация погрешностей5. По способу взаимодействия со значением
- 15. Классификация погрешностей6. По характеру поведения измеряемой величиныстатическая
- 16. Классификация погрешностей6. По характеру поведения измеряемой величиныИсходя
- 17. Классификация погрешностей7. По закономерности проявленияСистематическая – погрешность,
- 18. Законы распределенияНаиболее полной характеристикой случайной погрешности измерения
- 19. Законы распределения1. Нормальный закон распределенияДля нормального закона
- 20. Законы распределения1. Нормальный закон распределенияНормированная случайная величина:МЕТОДЫ ОПИСАНИЯ СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯСТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
- 21. Законы распределения1. Нормальный закон распределенияИнтегралы вероятностей:Теорема Ляпунова:Закон
- 22. Законы распределения2. Равномерный закон распределенияМЕТОДЫ ОПИСАНИЯ СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯСТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
- 23. Априорно неизвестный временной интервалЗакон распределения погрешности несинхронизированного
- 24. Априорно неизвестный временной интервал Синхронизированное
- 25. Фиксированный временной интервалЗАКОН РАСПРЕДЕЛЕНИЯ ПОГРЕШНОСТИ НЕСИНХРОНИЗИРОВАННОГО КВАНТОВАНИЯ ФИКСИРОВАННОГО ВРЕМЕННОГО ИНТЕРВАЛАСТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
- 26. Фиксированный временной интервалЗАКОН РАСПРЕДЕЛЕНИЯ ПОГРЕШНОСТИ НЕСИНХРОНИЗИРОВАННОГО КВАНТОВАНИЯ ФИКСИРОВАННОГО ВРЕМЕННОГО ИНТЕРВАЛАСТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
- 27. Доверительное значение погрешностиДоверительное значение погрешности соответствует половине
- 28. Доверительное значение погрешностиДля экспоненциальных законов распределения:где ε
- 29. Доверительное значение погрешностиВсе три зависимости пересекаются в
- 30. Показатели точности измеренийОбозначение погрешности в соответствии с
- 31. Показатели точности измеренийСтандартные распределения, рекомендации:Равномерный закон распределенияУсеченный
- 32. Погрешности косвенных измеренийПри косвенном измерении результаты, полученные
- 33. Погрешности косвенных измеренийгде Rxy – корреляционный момент погрешностей Δx и Δy.ПОГРЕШНОСТИ КОСВЕННЫХ ИЗМЕРЕНИЙСТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
- 34. Погрешности косвенных измеренийгде f(x,y) – совместная плотность
- 35. Погрешности косвенных измеренийПри работе с системой нескольких
- 36. Погрешности косвенных измеренийСреднеквадратическая погрешность результата косвенного измерения
- 37. Требования, предъявляемые к статистическим оценкамОценки истинного значения
- 38. Методы повышения эффективности оценокВ зависимости от полноты
- 39. Методы повышения эффективности оценокМетод наименьших квадратов (МНК)Суть
- 40. Методы повышения эффективности оценокМетод максимума функции правдоподобияФункцией
- 41. Определение доверительного значения погрешностиДоверительное значение погрешности оценки
- 42. Обработка неравноточных измеренийНеравноточными называются измерения, выполненные при
- 43. Обработка неравноточных измеренийЭффективность оценки обеспечивается минимизацией дисперсии:ОБРАБОТКА НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙСТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
- 44. Обработка неравноточных измеренийВеса результатов измерений должны быть
- 45. Обработка неравноточных измеренийВ случае равноточных измерений:Выражение для
- 46. Определение законов распределения по результатам многократных измеренийВыражение
- 47. Определение законов распределения по результатам многократных измеренийСтатистический
- 48. Определение законов распределения по результатам многократных измеренийГистограмма
- 49. Определение законов распределения по результатам многократных измеренийИз-за
- 50. Определение законов распределения по результатам многократных измеренийВ
- 51. Критерий ПирсонаСогласованность теоретического и статистического распределений проверяют
- 52. Критерий ПирсонаРаспределение χ2 зависит от параметра r,
- 53. Критерий ПирсонаТребование совпадения теоретической и статистической дисперсии:Распределение
- 54. Критерий КолмогороваВ качестве меры расхождения теоретического и
- 55. Критерий КолмогороваА.Н. Колмогоров доказал, что какова бы
- 56. Обнаружение промаховПромахом называется грубое искажение результатов измеренийПричинами
- 57. Обнаружение промаховРешение:По результатам x1,x2,…,xn находят оценку истинного
- 58. Обнаружение промаховОпределяют максимально допустимое отклонение результатов измерений
- 59. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Федеральное государственное образовательное учреждение
высшего профессионального образования
Сибирский
федеральный университет
Слайд 2СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Лекция 2. Статистическая теория погрешностей измерения
Институт инженерной
физики и радиоэлектроники
Направление 210200.62 Радиотехника
К.т.н., доцент кафедры РТ Алешечкин
Андрей МихайловичМетрология и радиоизмерения
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Федеральное государственное образовательное учреждение
высшего профессионального образования
Сибирский федеральный университет
Кафедра «Радиотехника»
Слайд 3План лекции
1 Классификация погрешностей
2 Методы описания случайных погрешностей измерения
3
Закон распределения погрешности несинхронизированного квантования априорно неизвестного временного интервала
4 Закон
распределения погрешности несинхронизированного квантования фиксированного временного интервала5 Доверительное значение погрешности
6 Показатели точности измерений, рекомендованные ГОСТ 8.011-72
7 Погрешности косвенных измерений
8 Цели статистической обработки результатов многократных измерений. Требования, предъявляемые к статистическим оценкам
9 Методы повышения эффективности оценок
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 4План лекции
10 Определение доверительного значения погрешности результата измерения
11 Обработка неравноточных
измерений
12 Определение законов распределения по результатам многократных измерений
13 Критерий Пирсона
14
Критерий Колмогорова15 Обнаружение промахов
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 5Погрешности измерений
При любой степени совершенства измерительной аппаратуры, при любой тщательности
погрешности выполнения, результат измерения всегда будет отличаться от истинного значения
измеряемой величины. При любых измерениях неизбежны погрешности.Физическая величина – свойство, общее в качественном отношении для многих физических объектов, но в количественном отношении – индивидуальное для каждого объекта.
Результат измерения с учетом погрешности измерений:
где Aизм – измеренное значение; A0 – истинное значение физической величины; ΔA – погрешность измерения.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 6Погрешности измерений
Абсолютная погрешность измерений:
Относительная погрешность измерений:
С учетом погрешности, результат измерения
записывается следующим образом:
256 мВ ± 0.3 мВ
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ
ИЗМЕРЕНИЯ
Слайд 7Классификация погрешностей
1. По слагаемым измерения
погрешность преобразования;
погрешность меры;
погрешность сравнения;
погрешность фиксации.
Для цифровых
приборов погрешность сравнения есть погрешность квантования, погрешность фиксации равна нулю
КЛАССИФИКАЦИЯ
ПОГРЕШНОСТЕЙСТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 8Классификация погрешностей
2. По источнику возникновения погрешности
методическая – погрешность метода измерения,
используемых формул и других упрощающих допущений;
аппаратурная (инструментальная) – данная погрешность
зависит от вида схемы и типов применяемых элементов;внешняя – от внешних условий эксплуатации прибора;
субъективная (личностная) – данная погрешность обусловлена личностными качествами оператора, т.е. разные операторы могут получить разные результаты измерений; все зависит от опыта, тщательности выполнения измерений и т.д.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 9Классификация погрешностей
3. По условиям проведения измерений
основная погрешность – погрешность средства
измерений, используемого в нормальных условиях эксплуатации;
дополнительная погрешность – погрешность средства
измерений, эксплуатируемого в условиях, отличающихся от нормальных.Условия проведения измерений: температура окружающей среды, давление, влажность, напряжение питающей сети.
В соответствии с ГОСТ 9763-67 нормальными считаются следующие условия:
температура: 20°C ± 5% – рабочие средства измерений, 20°С ± 10% – образцовые СИ;
влажность: 65% ± 15% при t = 200 С;
атмосферное давление: 750 мм рт. ст;
сеть: частота – 50 Гц, напряжение – 220 В ± 2%.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 10Классификация погрешностей
4. По способу выражения погрешности
абсолютная погрешность – погрешность определяемая
из выражения:
где Aизм – измеренное значение; A0 – истинное значение
физической величины; ΔA – погрешность измерения.относительная погрешность (обычно выражают в процентах):
приведенная погрешность средства измерений – отношение абсолютной погрешности к длине шкалы измерительного прибора, выражается, как правило, в процентах:
где L – длина шкалы измерительного прибора, ΔAmax - максимальное значение абсолютной основной погрешности измерительного прибора.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 11Классификация погрешностей
Класс точности
Класс точности измерительного прибора – обобщенная характеристика его
точности, но не непосредственный ее показатель. Класс точности измерительного прибора
δк.п. численно равен наибольшей допустимой приведенной основной погрешности, выраженной в процентах, δк.п.=δLA max .Значения классов точности измерительных приборов присваивают из ряда, составленного из следующих предпочтительных чисел:
где n = 1; 0; –1; –2; …
Значение максимальной абсолютной основной погрешности измерительного прибора можно вычислить по его классу точности:
При работе с многопредельными измерительными приборами необходимо проводить измерения вблизи конечного деления шкалы прибора, поскольку в этом случае относительная погрешность будет меньше.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 12Классификация погрешностей
5. По способу взаимодействия со значением измеряемой величины
Аддитивная погрешность
– это погрешность нуля прибора, она не зависит от текущего
значения измеряемой величины. ΔA0=constКЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 13Классификация погрешностей
5. По способу взаимодействия со значением измеряемой величины
Мультипликативная погрешность
– зависит от значения измеряемой величины.
где ΔAM – абсолютная мультипликативная
погрешность пропорциональная измеряемой величине; δAm - относительное значение мультипликативной погрешности, не зависящее от значения измеряемой величины.КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 14Классификация погрешностей
5. По способу взаимодействия со значением измеряемой величины
При наличии
аддитивной и мультипликативной погрешностей:
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 15Классификация погрешностей
6. По характеру поведения измеряемой величины
статическая погрешность Δст;
динамическая погрешность
Δд;
погрешность в динамическом режиме ΔΣ.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Диодный детектор
с открытым входомЗависимость напряжения на входе и на выходе детектора при подаче на его вход скачка напряжения
Зависимость напряжения на входе и на выходе детектора при подаче на его вход скачка нарастающего напряжения.
Слайд 16Классификация погрешностей
6. По характеру поведения измеряемой величины
Исходя из теории случайных
процессов, динамическую погрешность можно исключить если обеспечить выполнение условия:
где τкор
- время корреляции входного измеряемого сигнала; τпр=RC- постоянная времени прибора.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 17Классификация погрешностей
7. По закономерности проявления
Систематическая – погрешность, постоянная по величине
и знаку. Систематическую погрешность можно заранее изучить и исключить ее
путем введения соответствующих поправок.Для исключения влияния систематических погрешностей также применяют поверку измерительных приборов.
Поверкой называется совокупность действий, производимых с целью оценки погрешностей средств измерений и установления их пригодности к применению.
Случайная – погрешность, величина и знак которой заранее не могут быть предсказаны.
Ряд измерений, в которых присутствует случайная погрешность имеет, например вид: 21.0, 21.1, 21.2, 21.1.
Промах – это грубое искажение результатов измерений. Промахи должны быть исключены из обработки. Для этого существуют критерии их обнаружения, например критерий Романовского.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 18Законы распределения
Наиболее полной характеристикой случайной погрешности измерения является закон ее
распределения. К законам распределения погрешностей относятся функция распределения погрешности F(Δ)
или плотность распределения:Погрешности измерения могут иметь различные законы распределения.
МЕТОДЫ ОПИСАНИЯ СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 19Законы распределения
1. Нормальный закон распределения
Для нормального закона распределения плотность вероятности
f(Δ) задается в виде выражения:
где m – математическое ожидание погрешности,
σ – среднеквадратическое отклонение погрешности , представляющее собой квадратный корень из дисперсии погрешности.Функция распределения (интегральная) для нормального закона определяется как:
МЕТОДЫ ОПИСАНИЯ СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 20Законы распределения
1. Нормальный закон распределения
Нормированная случайная величина:
МЕТОДЫ ОПИСАНИЯ СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ
ИЗМЕРЕНИЯ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 21Законы распределения
1. Нормальный закон распределения
Интегралы вероятностей:
Теорема Ляпунова:
Закон распределения суммы независимых
случайных величин при большом их числе и при малом вкладе
каждой из них в суммарный процесс стремится к нормальному тем ближе, чем более n стремится к бесконечности.МЕТОДЫ ОПИСАНИЯ СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 22Законы распределения
2. Равномерный закон распределения
МЕТОДЫ ОПИСАНИЯ СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ
ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 23Априорно неизвестный временной интервал
Закон распределения погрешности несинхронизированного квантования априорно неизвестного
временного интервала
Измеритель временных интервалов:
ОИ – опорный импульс; ИИ – интервальный
импульс; Т – RS-триггер; СС – схема совпадений; ГТИ – генератор тактовых импульсов; СЧ – счетчик; Инд – цифровой индикаторЗАКОН РАСПРЕДЕЛЕНИЯ ПОГРЕШНОСТИ НЕСИНХРОНИЗИРОВАННОГО КВАНТОВАНИЯ АПРИОРНО НЕИЗВЕСТНОГО ВРЕМЕННОГО ИНТЕРВАЛА
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 24Априорно неизвестный временной интервал
Синхронизированное квантование: Несинхронизированное
квантование:
Распределение Δtн, Δtк: Распределение Симпсона:
ЗАКОН РАСПРЕДЕЛЕНИЯ
ПОГРЕШНОСТИ НЕСИНХРОНИЗИРОВАННОГО КВАНТОВАНИЯ АПРИОРНО НЕИЗВЕСТНОГО ВРЕМЕННОГО ИНТЕРВАЛАСТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 25Фиксированный временной интервал
ЗАКОН РАСПРЕДЕЛЕНИЯ ПОГРЕШНОСТИ НЕСИНХРОНИЗИРОВАННОГО КВАНТОВАНИЯ ФИКСИРОВАННОГО ВРЕМЕННОГО ИНТЕРВАЛА
СТАТИСТИЧЕСКАЯ
ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
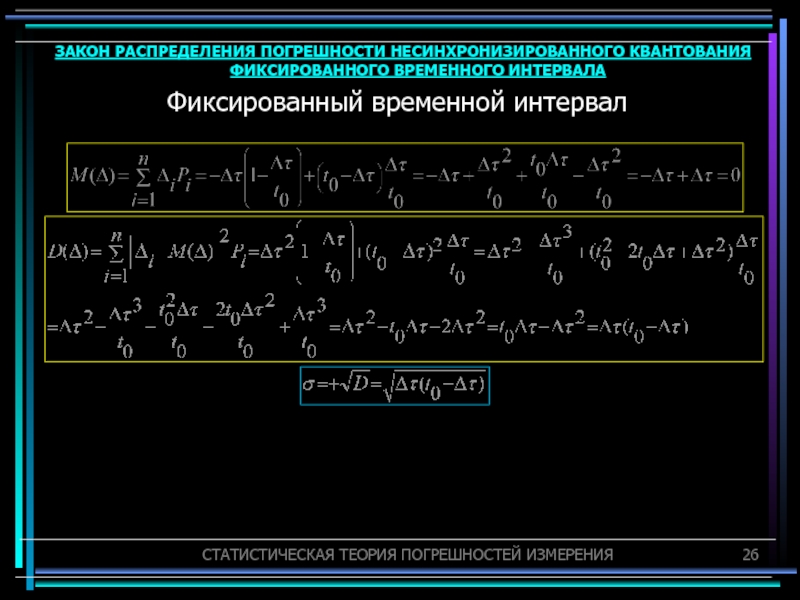
Слайд 26Фиксированный временной интервал
ЗАКОН РАСПРЕДЕЛЕНИЯ ПОГРЕШНОСТИ НЕСИНХРОНИЗИРОВАННОГО КВАНТОВАНИЯ ФИКСИРОВАННОГО ВРЕМЕННОГО ИНТЕРВАЛА
СТАТИСТИЧЕСКАЯ
ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 27Доверительное значение погрешности
Доверительное значение погрешности соответствует половине доверительного интервала при
заданной доверительной вероятности . Доверительное значение погрешности определяется на основе
решения следующего уравнения:где t – коэффициент, зависящий от вида закона распределения и значения доверительной вероятности.
ДОВЕРИТЕЛЬНОЕ ЗНАЧЕНИЕ ПОГРЕШНОСТИ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 28Доверительное значение погрешности
Для экспоненциальных законов распределения:
где ε –эксцесс распределения
Для уплощенных
законов распределения:
Для кругловершинных двумодальных законов распределения:
Для островершинных двумодальных законов распределения:
ДОВЕРИТЕЛЬНОЕ
ЗНАЧЕНИЕ ПОГРЕШНОСТИСТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
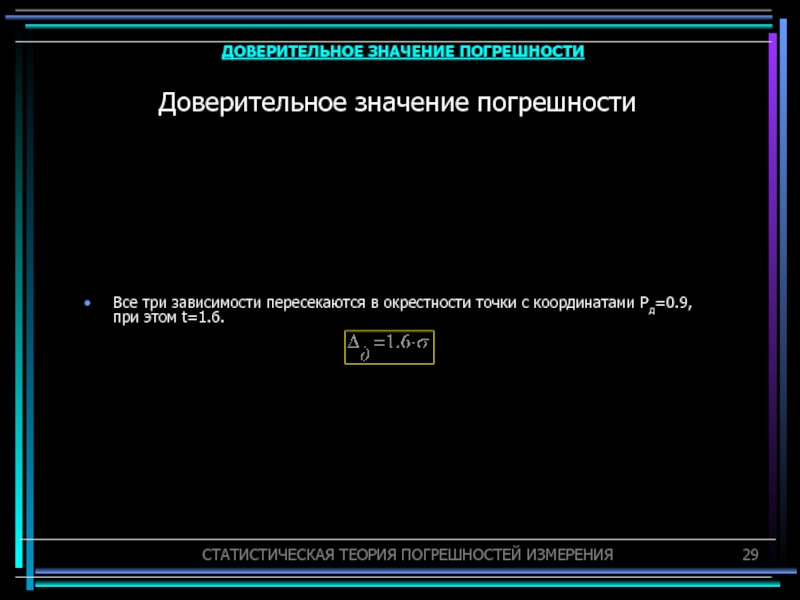
Слайд 29Доверительное значение погрешности
Все три зависимости пересекаются в окрестности точки с
координатами Pд=0.9, при этом t=1.6.
ДОВЕРИТЕЛЬНОЕ ЗНАЧЕНИЕ ПОГРЕШНОСТИ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 30Показатели точности измерений
Обозначение погрешности в соответствии с ГОСТ 8.011–72:
где Δ
– общая (суммарная) погрешность измерения, Δс – систематическая
составляющая погрешности измерения,
– случайная составляющая погрешности.В соответствии с ГОСТ, точность измерений выражается следующими способами:
Интервалом, в котором с установленной вероятностью находиться суммарная погрешность измерения.
Интервалом, в котором с установленной вероятность находиться систематическая составляющая погрешности измерения, стандартной аппроксимацией функции распределения случайной погрешности измерения и ее среднеквадратическим значением.
ПОКАЗАТЕЛИ ТОЧНОСТИ ИЗМЕРЕНИЙ, РЕКОМЕНДОВАННЫЕ ГОСТ 8.011-72
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 31Показатели точности измерений
Стандартные распределения, рекомендации:
Равномерный закон распределения
Усеченный нормальный
Усеченный релеевский
Островершинный и
плосковершинный закон распределения.
Стандартными аппроксимациями функций распределения статистической и случайной составляющих
погрешностей измерения и их средними квадратическими отклонениями.Функциями распределения систематической и случайной составляющих погрешности измерения.
ПОКАЗАТЕЛИ ТОЧНОСТИ ИЗМЕРЕНИЙ, РЕКОМЕНДОВАННЫЕ ГОСТ 8.011-72
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 32Погрешности косвенных измерений
При косвенном измерении результаты, полученные прямыми измерениями, являются
исходными данными для дальнейших вычислений. Наличие погрешности прямых измерений приводит
к тому, что окончательный результат, т.е. результат косвенного измерения, также имеет погрешность.Примером косвенных измерений является задача определения коэффициента передачи цепи.
Рассмотрим простейший случай, когда неизвестная величина является непрерывной и дифференцируемой функцией двух других величин x и y, определяемых результатами прямых измерений:
С учетом погрешностей, выражение может быть записано в виде:
Разложим функцию f(x,y) в ряд Тейлора в окрестностях точки Ax, Ay :
ПОГРЕШНОСТИ КОСВЕННЫХ ИЗМЕРЕНИЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 33Погрешности косвенных измерений
где Rxy – корреляционный момент погрешностей Δx и
Δy.
ПОГРЕШНОСТИ КОСВЕННЫХ ИЗМЕРЕНИЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 34Погрешности косвенных измерений
где f(x,y) – совместная плотность распределения случайных величин
x и y.
Коэффициент корреляции:
ПОГРЕШНОСТИ КОСВЕННЫХ ИЗМЕРЕНИЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 35Погрешности косвенных измерений
При работе с системой нескольких случайных величин, корреляционные
моменты связи записывают в виде корреляционной матрицы:
В случае, если величины
некоррелированы:ПОГРЕШНОСТИ КОСВЕННЫХ ИЗМЕРЕНИЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 36Погрешности косвенных измерений
Среднеквадратическая погрешность результата косвенного измерения определяется в соответствии
с выражением:
Если случайные величины некоррелированы:
В случае, когда результат косвенного измерения
является функцией n прямых измерений, получим:ПОГРЕШНОСТИ КОСВЕННЫХ ИЗМЕРЕНИЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 37Требования, предъявляемые к статистическим оценкам
Оценки истинного значения измеряемой величины и
ее погрешности является статистическими оценками.
Требования, предъявляемые к статистическим оценкам:
Состоятельность
Оценка некоторой
истинной величины называется состоятельной, если при увеличении числа измерений она стремится к истинному значению оцениваемой величины:Несмещенность
Оценка называется несмещенной, если ее математическое ожидание равно истинному значению оцениваемой величины
Эффективность
Оценка называется эффективной, если она обладает наименьшей дисперсией из всех возможных оценок
ЦЕЛИ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ РЕЗУЛЬТАТОВ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К СТАТИСТИЧЕСКИМ ОЦЕНКАМ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 38Методы повышения эффективности оценок
В зависимости от полноты имеющейся измерительной информации
и допустимой сложности алгоритмов оценивания используются следующие способы оптимизации оценок,
приведенные в порядке усложнения алгоритмов оценивая и увеличения полноты имеющейся информации:Наименьших квадратов.
Взвешенных наименьших квадратов. Необходимо знать дисперсии результатов измерений
Средний квадратический. Необходимо знать числовые характеристики системы случайных величин
Максимального правдоподобия. Необходимо знание законов распределения результатов измерений
Максимума апостериорной вероятности (Байесовский критерий). Необходимо знать совместные плотности распределения результатов измерений и оценок: , и априорную плотность распределения оценки
МЕТОДЫ ПОВЫШЕНИЯ ЭФФЕКТИВНОСТИ ОЦЕНОК
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 39Методы повышения эффективности оценок
Метод наименьших квадратов (МНК)
Суть МНК состоит в
минимизации суммы квадратов разностей результатов измерений и оценки:
При отсутствии априорных
данных об измеряемой величине, в качестве оценки истинного значения следует брать среднее арифметическое измеренных значенийМЕТОДЫ ПОВЫШЕНИЯ ЭФФЕКТИВНОСТИ ОЦЕНОК
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 40Методы повышения эффективности оценок
Метод максимума функции правдоподобия
Функцией правдоподобия оценки называется
условная плотность распределения:
Эффективная
оценка соответствует максимуму функции правдоподобияМЕТОДЫ ПОВЫШЕНИЯ ЭФФЕКТИВНОСТИ ОЦЕНОК
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 41Определение доверительного значения погрешности
Доверительное значение погрешности оценки истинного значения результата
измерения можно рассчитать по формуле:
где - статистическая оценка среднеквадратической
погрешности исходных данных; - оценка истинного значения измеряемой величины, найденная по n результатам измеренийПри нормальном законе распределения исходных данных доверительное значение погрешности оценки, полученной путем усреднения, находят с использованием распределения Стьюдента, которое имеет случайная величина:
доверительное значение погрешности оценки истинного значения находят с использованием соотношения:
ОПРЕДЕЛЕНИЕ ДОВЕРИТЕЛЬНОГО ЗНАЧЕНИЯ ПОГРЕШНОСТИ РЕЗУЛЬТАТА ИЗМЕРЕНИЯ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 42Обработка неравноточных измерений
Неравноточными называются измерения, выполненные при различных условиях.
Математические ожидание
результатов этих измерений одинаково, если они независимы и свободны от
систематических погрешностей:Среднеквадратические погрешности таких измерений различны:
Для оценки действительного значения измеряемой величины используют общее арифметическое среднее, также называемое как среднее взвешенное или весовое среднее, определяемое в соответствии в выражением:
где gi - вес i-го результата измерения
Значения весовых коэффициентов определяют так, чтобы оценка истинного значения была несмещенной:
ОБРАБОТКА НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 43Обработка неравноточных измерений
Эффективность оценки обеспечивается минимизацией дисперсии:
ОБРАБОТКА НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ
ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 44Обработка неравноточных измерений
Веса результатов измерений должны быть обратно пропорциональны дисперсиям
результатов соответствующих измерений:
ОБРАБОТКА НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 45Обработка неравноточных измерений
В случае равноточных измерений:
Выражение для нахождения среднего арифметического
является частным случаем общего арифметического среднего, используемого для оценки истинного
значения результатов неравноточных измерений.Учет с соответствующими весами всех результатов измерений, в том числе и грубых, приводит к уменьшению среднеквадратической погрешности оценки по сравнению с результатами наиболее точных измерений.
ОБРАБОТКА НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 46Определение законов распределения по результатам многократных измерений
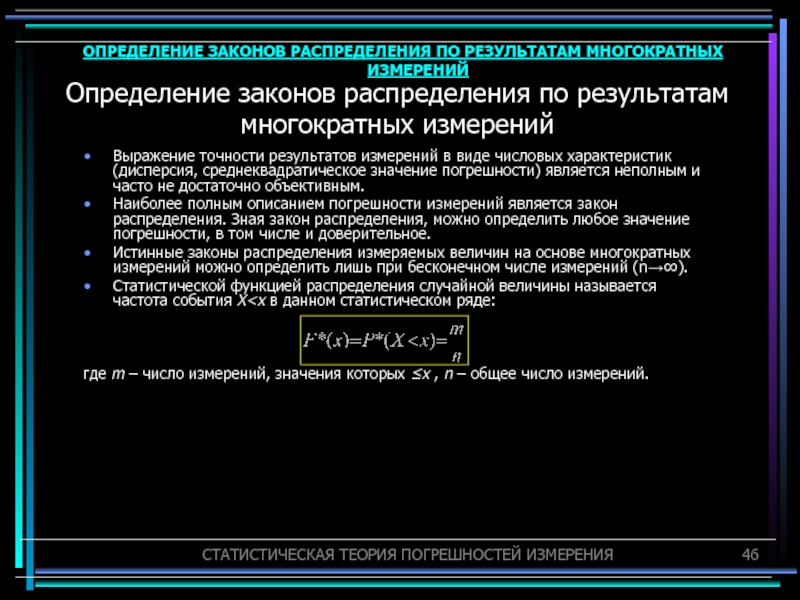
Выражение точности результатов измерений
в виде числовых характеристик (дисперсия, среднеквадратическое значение погрешности) является неполным
и часто не достаточно объективным.Наиболее полным описанием погрешности измерений является закон распределения. Зная закон распределения, можно определить любое значение погрешности, в том числе и доверительное.
Истинные законы распределения измеряемых величин на основе многократных измерений можно определить лишь при бесконечном числе измерений (n→∞).
Статистической функцией распределения случайной величины называется частота события X
где m – число измерений, значения которых ≤x , n – общее число измерений.
ОПРЕДЕЛЕНИЕ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ПО РЕЗУЛЬТАТАМ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 47Определение законов распределения по результатам многократных измерений
Статистический ряд строят в
следующей последовательности:
Результаты измерений располагают в порядке их возрастания, т.е. в
вариационный ряд.Полученный ряд делят на m разрядов, для каждого из которых находят частоту, соответствующую данному разряду.
Статистический ряд часто оформляют в виде графика, которой называется гистограммой:
Гистограмма строится таким образом, чтобы значения площади каждого из разрядов были равны значению статистической частоты каждого из разрядов
ОПРЕДЕЛЕНИЕ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ПО РЕЗУЛЬТАТАМ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 48Определение законов распределения по результатам многократных измерений
Гистограмма представляет собой статистический
аналог плотности распределения f(x).
Высота каждого из разрядов должна быть равна:
Используя
данные статистического ряда можно приближенно построить статистическую функцию распределения F*(x). В качестве точек для вычисления значений F*(x) удобно брать границы статистического ряда x1,x2,…,xm+1 .ОПРЕДЕЛЕНИЕ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ПО РЕЗУЛЬТАТАМ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 49Определение законов распределения по результатам многократных измерений
Из-за ограниченного набора измерений,
возникают отклонения теоретического распределения от статистического. Данные отклонения могут быть
вызваны следующим:Чисто случайные причины;
Неверно подобран закон распределения.
Для решения этой задачи существуют критерии согласия, позволяющие ответить на вопрос, правильно ли подобран закон распределения.
Для проверки согласия вводится некоторая величина U, характеризующую степень расхождения теоретического и статистического распределения.
Величина U может быть выбрана различными способами, например в качестве U можно взять сумму квадратов отклонений теоретических вероятностей Pi и соответствующих частот Pi*.
ОПРЕДЕЛЕНИЕ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ПО РЕЗУЛЬТАТАМ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 50Определение законов распределения по результатам многократных измерений
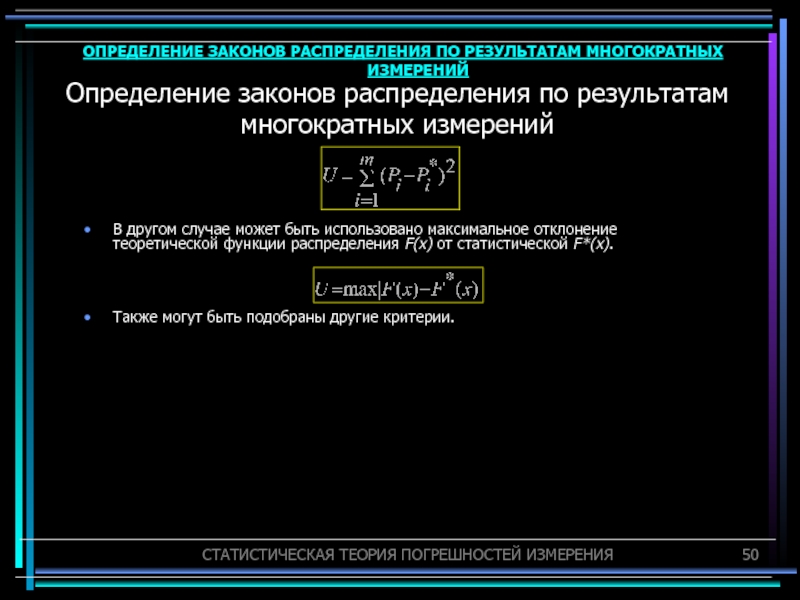
В другом случае может
быть использовано максимальное отклонение теоретической функции распределения F(x) от статистической
F*(x).Также могут быть подобраны другие критерии.
ОПРЕДЕЛЕНИЕ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ПО РЕЗУЛЬТАТАМ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 51Критерий Пирсона
Согласованность теоретического и статистического распределений проверяют по расхождению между
теоретическими вероятностями и частотами. Естественно выбрать в качестве меры расхождения
между теоретическими и систематическими распределениями сумму квадратов отклонений (Pi*-Pi), взятых с некоторыми весами Ci.Веса разрядов Ci, необходимо брать обратно пропорциональными вероятностям разрядов Pi.
К. Пирсон показал, что если выбрать , то при больших n закон распределения величины f(U) обладает весьма простыми свойствами:
Он практически не зависит от функции распределения F(x) и от числа опытов n;
Зависит только от числа разрядов m, а именно, при увеличении n закон распределения f(U) приближается к так называемому распределению χ2.
где m –число разрядов статистического ряда.
КРИТЕРИЙ ПИРСОНА
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 52Критерий Пирсона
Распределение χ2 зависит от параметра r, называемого числом степеней
свободы распределения. Число степеней свободы равно:
где m – число разрядов
статистического ряда, s – число наложенных связей.На распределение могут быть наложены следующие связи:
Сумма частот разрядов должна быть равна 1. Данное требование выполняется всегда.
Условие равенства математических ожиданий статистического ряда и теоретической функции распределения случайной величины:
где – cредина i–го разряда статистического ряда, mx - теоретическое значение математического ожидания.
КРИТЕРИЙ ПИРСОНА
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 53Критерий Пирсона
Требование совпадения теоретической и статистической дисперсии:
Распределение χ2 дает возможность
оценить степень согласования теоретического и статистического распределений.
Вероятность P, определенная по
таблице, есть вероятность того, что за счет чисто случайных причин мера расхождения теоретического и статистического распределений будет не меньше, чем фактически полученное в серии измерений значение χ2 . Если P<0.1, то результат измерений следует считать противоречащим гипотезе о том, что закон распределения величины x есть F(x).Если вероятность велика, то можно сказать, что с такой вероятностью закон распределения соответствует теоретическому.
КРИТЕРИЙ ПИРСОНА
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 54Критерий Колмогорова
В качестве меры расхождения теоретического и статистического распределений А.Н.
Колмогоров предположил максимальное значение модуля разности статистической функции распределения F*(x)
и соответствующей теоретической функции распределения F(x):Критерий Колмогорова своей простотой выгодно отличается от рассмотренного ранее критерия Пирсона χ2, поэтому его весьма охотно применяют на практике.
КРИТЕРИЙ КОЛМОГОРОВА
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 55Критерий Колмогорова
А.Н. Колмогоров доказал, что какова бы ни была F(x),
при неограниченном возрастании числа измерений n вероятность неравенства
стремится к пределу:Критерий Колмогорова можно использовать только в том случае, если гипотетическое распределение F(x) полностью известно заранее из каких-либо теоретических предпосылок, т.е. когда известен не только вид F(x), но и входящие в нее числовые параметры.
КРИТЕРИЙ КОЛМОГОРОВА
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 56Обнаружение промахов
Промахом называется грубое искажение результатов измерений
Причинами промахов могут быть
следующие:
неправильный отсчет по шкале измерительного прибора, происходящий из–за неверного учета
цепи малых делений шкалы;неправильная запись результата измерения;
ошибки при манипуляции с приборами или частями измерительной установки;
ошибки, вызванные сбоями аппаратуры, скачками, возникающими в питающей сети.
Для обнаружения промахов может быть использовано отбрасывание результатов, содержащих погрешности, превышающие значения 2σ,3σ,3.5σ.
Более строгий результат при определении промахов дает критерий Романовского.
Постановка задачи:
Проведено n+1 измерение случайной величины x: x1,x2,…,xn,xn+1. Значение xn+1 является подозрительным.
Необходимо определить, промах это или нет.
ОБНАРУЖЕНИЕ ПРОМАХОВ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
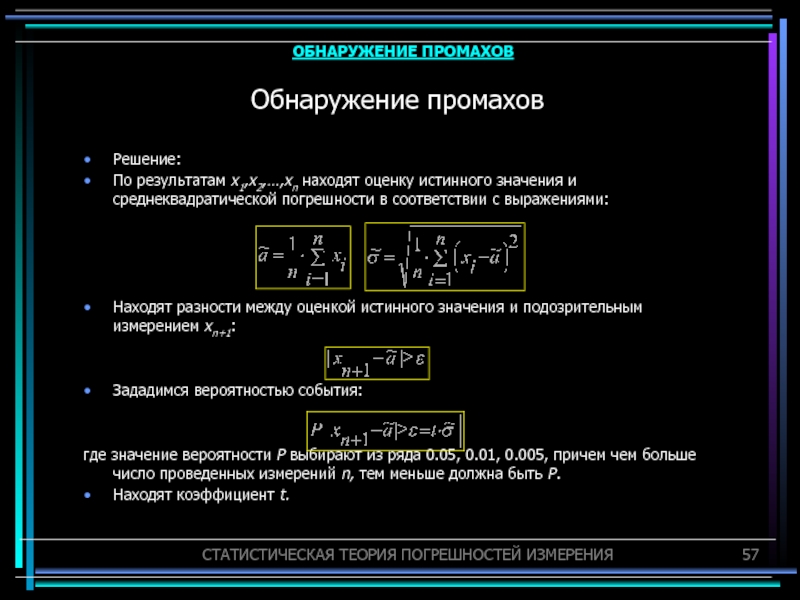
Слайд 57Обнаружение промахов
Решение:
По результатам x1,x2,…,xn находят оценку истинного значения и среднеквадратической
погрешности в соответствии с выражениями:
Находят разности между оценкой истинного значения
и подозрительным измерением xn+1:Зададимся вероятностью события:
где значение вероятности P выбирают из ряда 0.05, 0.01, 0.005, причем чем больше число проведенных измерений n, тем меньше должна быть P.
Находят коэффициент t.
ОБНАРУЖЕНИЕ ПРОМАХОВ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Слайд 58Обнаружение промахов
Определяют максимально допустимое отклонение результатов измерений от оценки истинного
значения:
Если:
то xn+1 является промахом;
если:
то xn+1 не является промахом и должно
быть оставлено в полученном ряде измерений.ОБНАРУЖЕНИЕ ПРОМАХОВ
СТАТИСТИЧЕСКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ