Статистические системы

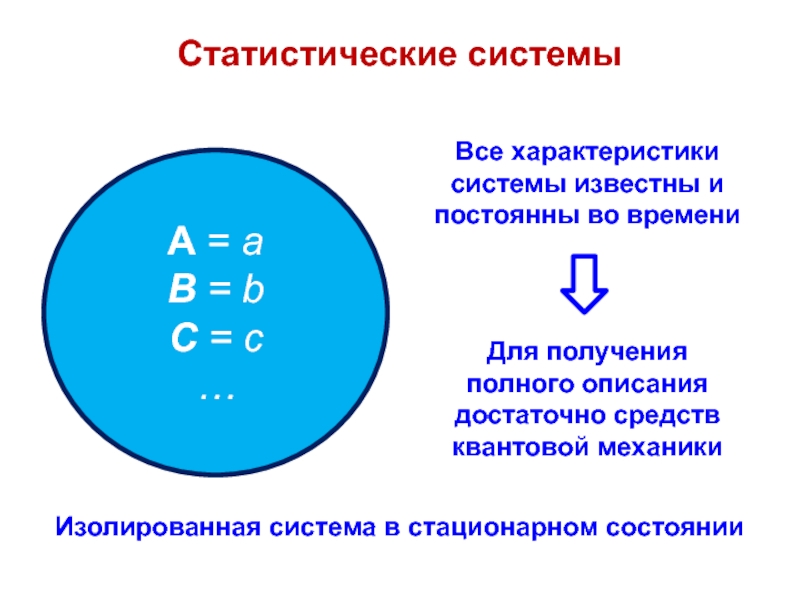
в стационарном состоянии
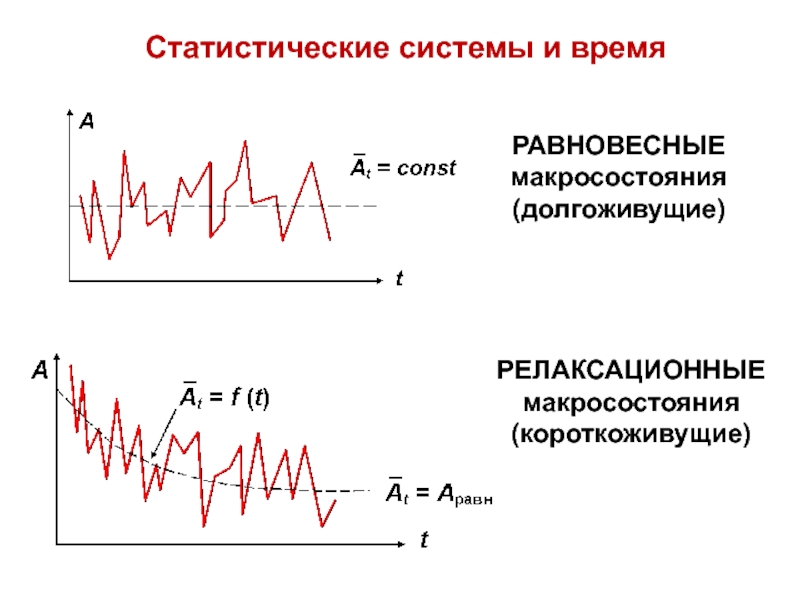
Все характеристики системы известны и постоянны во времени
Для

= ???
Такой вопрос является некорректным в рамках обычной механики, поскольку

Необходимо изменение методологии механики:

МИКРО-наблюдаемые

МАКРО-наблюдаемые

результатов измерения к СРЕДНИМ ПО ВРЕМЕНИ:
Аi → At

Ai = f ( Bi, Ci , …) ⎯→ At = f (Bt, Ct , …)

Вся логическая схема механицизма (состояния и уравнения состояния) сохраняется:

с последующим усреднением по большому временному интервалу
Использование модели статистического ансамбля

вероятности одинаковы
Aa = (1/6) (1 + 2 + 3 +

(число частиц) N = const
КАНОНИЧЕСКИЙ ансамбль (КА)
E ≠ const;

БОЛЬШОЙ КАНОНИЧЕСКИЙ ансамбль (БКА)
E ≠ const; N ≠ const

Рn = 1/Ω
где Ω — число допустимых состояний
Пример №

+ (SZ)2 + … + (SZ)10

–4 –3 –2 –1 0

Локальная проекция
(SZ )i /  = { –1/2 +1/2 }
P = { 1/2 1/2 }

+4) = 10

ЛОКАЛЬНЫХ состояний (различимых «изнутри»)
Ω = ∑ Ωi = 1024
Все локальные

Больцмана
Ωi → ln Ωi = σi
σi — статистическая энтропия i-го

Si = k ⋅ ln Ω i = k ⋅ σi

Числа доступных состояний ( Ωi ) для реальных систем чрезвычайно велики.
Поэтому для удобства вычислений пользуются их логарифмами (натуральными):

на то, что система находится в контакте с окружающей средой.

энтропии
Релаксация неравновесных систем

возрастанием энтропии; процессы с уменьшением энтропии могут протекать только вынужденно,

имеет статистического характера (не приводит к флуктуациям значений наблюдаемых) и

4ε, 5ε, 6ε, 7ε }
Допустимые состояния термостатированной системы
Каждое состояние может

∑е–Еi/θ
E — энергия
θ — статистическая температура
Q — статистическая сумма
θ

от калибровки шкалы энергии.
Вероятности Pi = е–Еi/θ/Q не

E = ∑ [ Ei ⋅ е–Еi/θ ] / Q

E = ∑ [ gi ⋅ Ei ⋅ е–Еi/θ ] / Q

Вычисление средних по ансамблю

(суммирование по состояниям)

(суммирование по энергетическим уровням, gi — статистический вес i-го уровня)

статистических сумм следует пользоваться специальной шкалой энергии — статистической

показывающей меру ее «статистичности» и степень влияния термостата на ее

свободная энергия F = – θ ln Q
внутренняя энергия U = θ2 (d ln Q / dθ)
энтропия σ = d (θ ln Q) / dθ

Q = Q1 ⋅ Q2 ⋅ … ⋅ Qn

"подстраиваться" под его температуру

ящик в контакте с электронным газом»

= (1/Z) ⋅ exp[–(E – μ1⋅N1 – μ2⋅N2 – …

Функция распределения БКА

Z — большая статистическая сумма (интеграл)

ХИМИЧЕСКИЙ ПОТЕНЦИАЛ
— средняя химическая энергия одной частицы хемостата

одном и том же объеме пространства, мешают друг другу

(частицы

О2 Не

О2 Не Не

О2 Не Не Не

( ΔΕхим < 0 )
Процесс обратим
Процесс необратим

μ = θ ln λ
P = (1/Z) ⋅ e–Е/θ

(q — теплота адсорбции)

η — доля занятой поверхности
η = f (T, p)

P1 = 1 – η

P2 = η

= 1/Z и P2

Большая статистическая сумма

Z = exp [– (E1 – μN1)/θ] + exp [– (E2 – μN2)/θ] =
= exp [– (0 – μ0)/θ] + exp [– (q – μ)/θ] =
= 1 + λ ⋅ exp (– q/θ)

где р = λ — давление газа,
b = exp(–q/θ) — адсорбционный коэффициент

Изотерма Лэнгмюра

равновесие: θсистемы = θтермостата

незаметным и мы можем пользоваться классической статистикой Больцмана – Гиббса

частиц-бозонов)
Ферми-Дирака (для частиц-фермионов)

энергии, и поэтому мы на их фоне не замечаем необычного

При низких температурах практически все частицы заселяют именно нижние уровни энергии, и поэтому их необычное поведение становится определяющим. Различие в поведении бозонов и фермионов становится макроскопическим (например, сверхтекучесть бозонных систем и др.).

Для атомов и молекул критическая температура составляет около 1-2 К
Для электронов — несколько тысяч кельвинов (статистическое поведение проявляется в плазме)