Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
STATISTICKÁ INDUKCE
Содержание
- 1. STATISTICKÁ INDUKCE
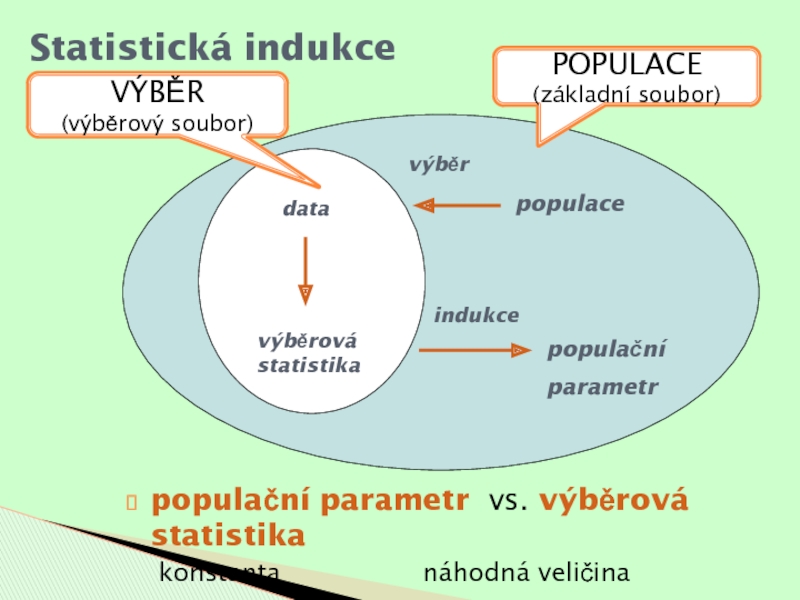
- 2. populacevýběrdatavýběrová statistikaindukcepopulačníparametrStatistická indukcePOPULACE (základní soubor)VÝBĚR (výběrový soubor)populační parametr vs. výběrová statistika konstanta náhodná veličina
- 3. Příkladpopulace: všichni studenti oboru PaA – kurzu
- 4. Statistické šetření – úplné (census)neúplnévýběrové(rychlejší, levnější)reprezentativnost výběruStatistické šetření
- 5. výběr na základě dobrovolnosti (anketa)výběr na základě
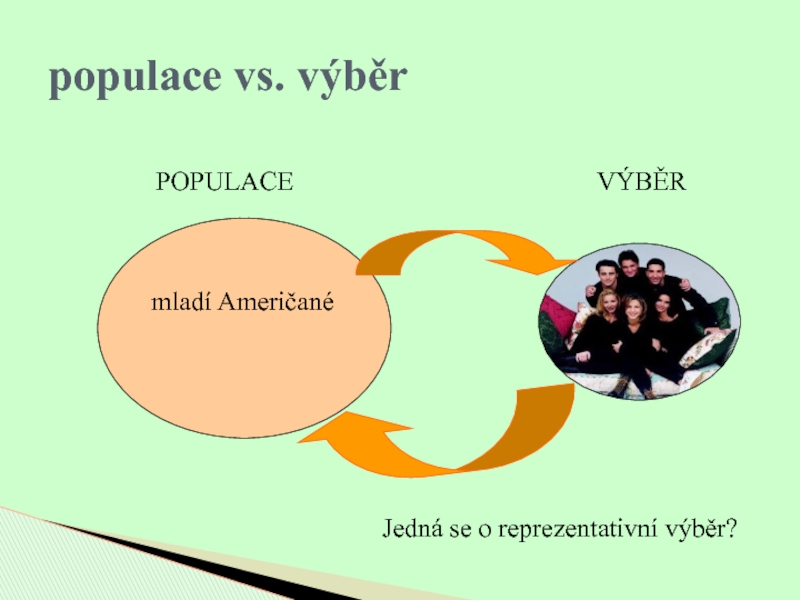
- 6. mladí AmeričanéPOPULACEVÝBĚRJedná se o reprezentativní výběr?populace vs. výběr
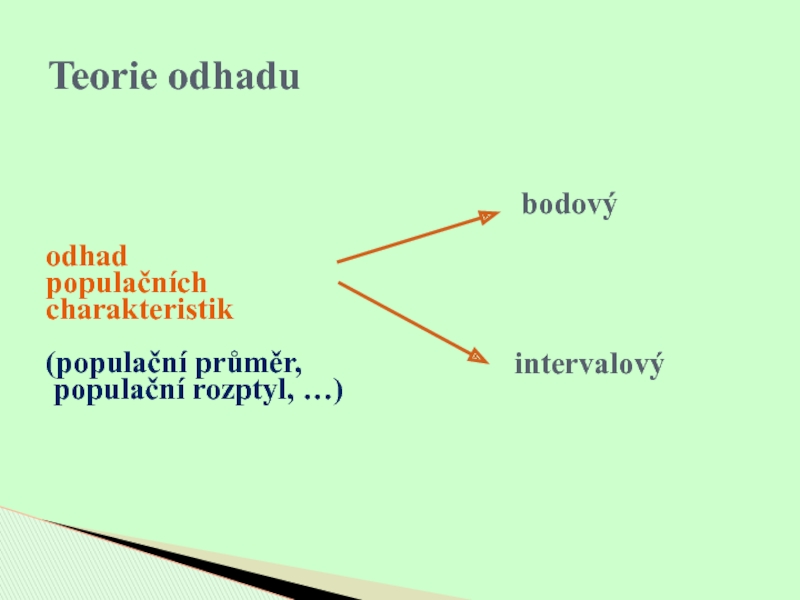
- 7. Teorie odhaduodhadpopulačních charakteristik(populační průměr, populační rozptyl, …)bodovýintervalový
- 8. Bodový odhadT bodový odhad populačního parametru θŽádoucí
- 9. rozptyl výběrového průměru σ2/nvýběrový průměr je nestranným
- 10. Bodový odhad populačního rozptylu a populační směrodatné
- 11. Značení
- 12. Intervalový odhadHodnotu populačního parametru Θ odhadneme číselným
- 13. Слайд 13
- 14. Jednostranné intervaly spolehlivostiP(- ∞ < Θ <
- 15. Interval spolehlivosti pro populační průměr μPředpoklad: výběr
- 16. uα…kritická hodnota normálního rozdělení pro hladinu významnosti
- 17. tα(f)…kritická hodnota Studentova t-rozdělení pro hladinu významnosti
- 18. Obyvatelé domků u frekventované silnice si stěžují
- 19. intervalový odhad 95% interval spolehlivosti pro μ Příklad
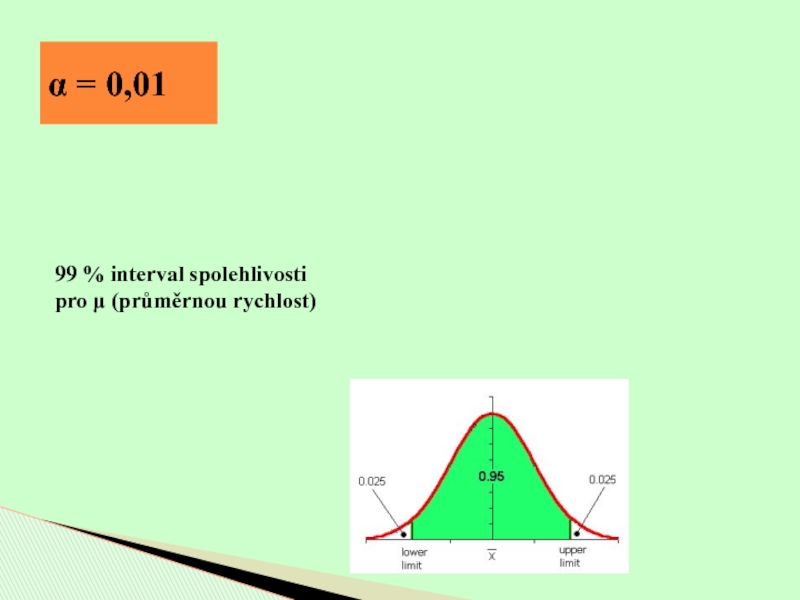
- 20. α = 0,0199 % interval spolehlivosti pro μ (průměrnou rychlost)
- 21. U kolika automobilů by musela být rychlost
- 22. Intervalový odhad rozptyluPředpoklad: výběr z populace s
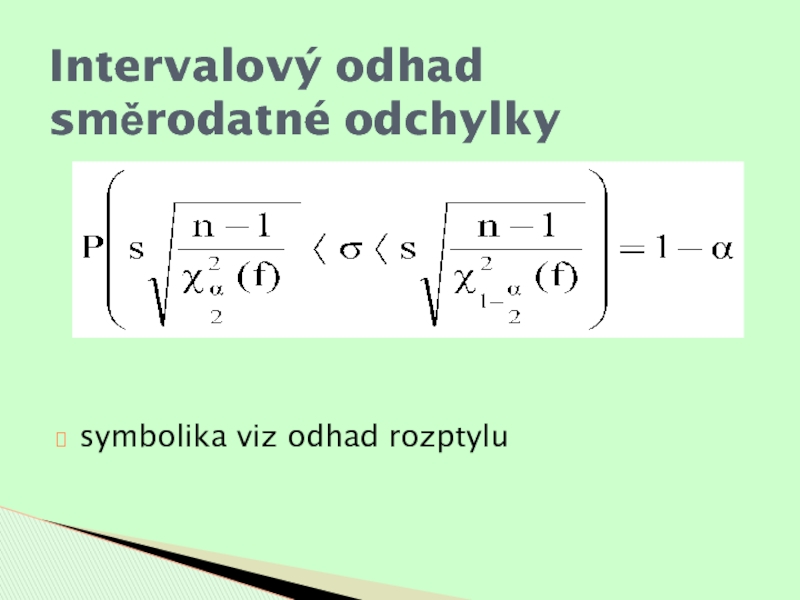
- 23. symbolika viz odhad rozptyluIntervalový odhad směrodatné odchylky
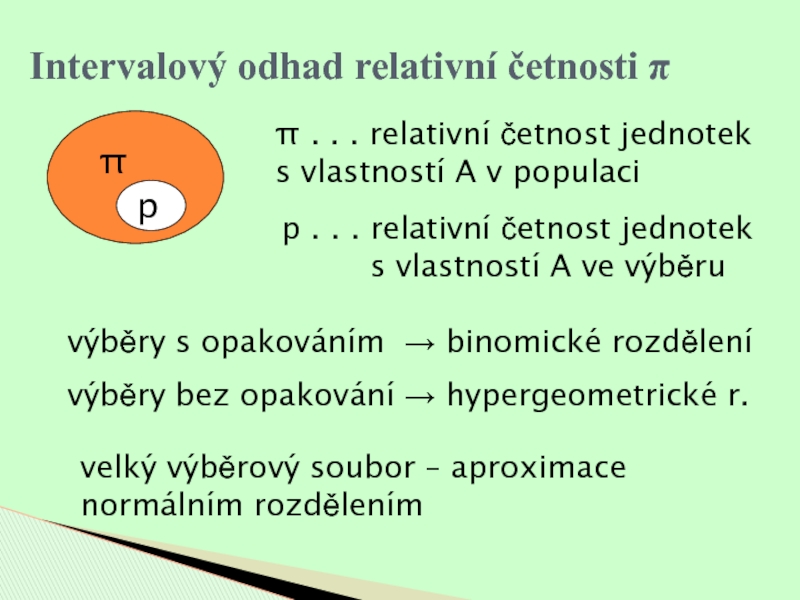
- 24. Intervalový odhad relativní četnosti ππ . .
- 25. Předpoklad: velký rozsah výběru interval spolehlivosti pro
- 26. PříkladV náhodném výběru 400 studentů je 88
- 27. Neparametrický odhad mediánucitlivost aritmetického průměru na vybočující
- 28. P(xk ≤ M ≤ xn-k+1) ≥ 1
- 29. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2populace
výběr
data
výběrová statistika
indukce
populační
parametr
Statistická indukce
POPULACE (základní soubor)
VÝBĚR
(výběrový soubor)
populační parametr vs. výběrová
statistika
Слайд 3Příklad
populace: všichni studenti oboru PaA – kurzu Statistika I
PaA, ZS 2013/2014
průměrný bodový zisk z prvního zápočtového testu pro všechny studenty byl 12,06 bodů
výběry
n1=30;
n2=26;
n3=50;
n4=22;
n5=28;
n6=25;
n7=35;
........
Výběrová charakteristika – náhodná veličina s určitou variabilitou!
Populační parametr – konstanta!
μ =12,06
Слайд 4Statistické šetření –
úplné (census)
neúplné
výběrové
(rychlejší, levnější)
reprezentativnost výběru
Statistické šetření
Слайд 5výběr na základě dobrovolnosti (anketa)
výběr na základě dostupnosti
kvótní výběr
náhodný výběr
prostý
náhodný výběr
každý
výběrový soubor o rozsahu n má stejnou ppst výběru(= každý prvek populace má stejnou ppst, že bude vybrán)
Způsoby výběru
Слайд 7Teorie odhadu
odhad
populačních
charakteristik
(populační průměr,
populační rozptyl, …)
bodový
intervalový
Слайд 8Bodový odhad
T bodový odhad populačního parametru θ
Žádoucí vlastnosti výběrové statistiky,
kterou použiji k odhadu
konzistentní – s rostoucím počtem pozorování
se odhad blíží k hodnotě populačního parametru s pravděpodobností 1nestranná – při opakovaných výběrech kolísá odhad tak, že v průměru se odhady z výběrů rovnají populační hodnotě, tj. střední hodnota výběrové statistiky se rovná odhadovanému populačnímu parametru, jde o nestranný odhad (E(T) = θ)
vydatná – rozptyl odhadů při opakovaných výběrech je malý
postačující – neexistuje další statistika, která by obsahovala o odhadované pop. charakteristice další informaci
Слайд 9rozptyl výběrového průměru σ2/n
výběrový průměr je nestranným odhadem populačního průměru
směrodatná
odchylka výběr. průměru σ/√n
směrodatná chyba výběrového průměru
ukazatel variability výběrových průměrů
Bodový
odhad průměruСлайд 10Bodový odhad populačního rozptylu a populační směrodatné odchylky
nestranným odhadem
populačního rozptylu je výběrový rozptyl
odhad populační směrodatné odchylky
je pouze
asymptoticky nestrannýs rostoucím rozsahem souboru se vychýlení zmenšuje
Слайд 12Intervalový odhad
Hodnotu populačního parametru Θ odhadneme číselným intervalem, který s
předem zvolenou pravděpodobností obsahuje odhadovaný populační parametr Θ .
1-α .
. . spolehlivost odhadu (koeficient spolehlivosti)α . . . hladina významnosti
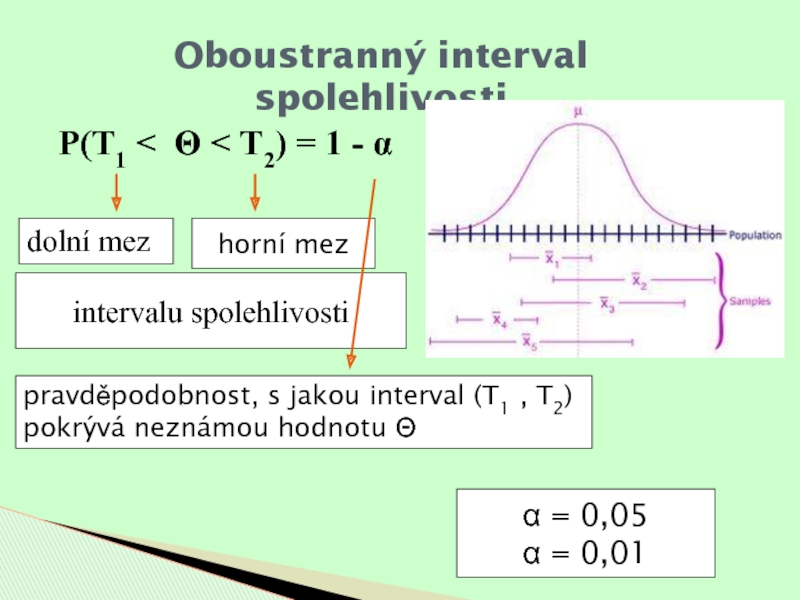
P(T1 < Θ < T2) = 1 - α
Слайд 13
P(T1 < Θ < T2) = 1 - α
dolní mez
horní
mez
intervalu spolehlivosti
pravděpodobnost, s jakou interval (T1 , T2) pokrývá neznámou
hodnotu ΘOboustranný interval spolehlivosti
α = 0,05
α = 0,01
Слайд 14Jednostranné intervaly spolehlivosti
P(- ∞ < Θ < T2) = 1
– α
pravostranný interval spolehlivosti
P(T1 < Θ < + ∞ )
= 1 – αlevostranný interval spolehlivosti
Слайд 15Interval spolehlivosti pro populační průměr μ
Předpoklad: výběr z velké populace
s normálním rozdělením N(μ,
σ2)Δ . . . přípustná chyba odhadu
oboustranný interval spolehlivosti
Слайд 16uα…kritická hodnota normálního rozdělení pro hladinu významnosti α
σ...populační směrodatná odchylka
n…rozsah
výběrového souboru
Odhad při známém populačním rozptylu σ2
Слайд 17tα(f)…kritická hodnota Studentova t-rozdělení pro hladinu významnosti α a f=n-1
st. vol.
s…výběrová směrodatná odchylka
n…rozsah výběrového souboru
Odhad při neznámém populačním
rozptylu σ2Слайд 18Obyvatelé domků u frekventované silnice si stěžují na vysokou rychlost
projíždějících automobilů. Pro 30 náhodně vybraných automobilů byla zjištěna rychlost
v km.Odhadněte pomocí bodového i intervalového odhadu (α = =0,05), jaká je průměrná rychlost projíždějících vozidel.
bodový odhad průměrné rychlosti
Příklad
Слайд 19
intervalový odhad
95% interval spolehlivosti pro μ
Příklad - pokračování
95 %
interval spolehlivosti pro μ:
(skutečnou průměrnou
rychlost)tento interval s 95 % pravděpodobností pokrývá neznámou hodnotu populačního průměru
Слайд 21U kolika automobilů by musela být rychlost měřena, aby bylo
možné na 5% hladině významnosti odhadnout populační průměr s maximální
přípustnou chybou 1 km?Příklad - pokračování
stanovení rozsahu výběru
Слайд 22Intervalový odhad rozptylu
Předpoklad: výběr z populace s normálním
rozdělením N(μ,
σ2), parametr μ je neznámý
kritické hodnoty χ2 rozdělení s
f
= n-1 stupni volnosti Слайд 24Intervalový odhad relativní četnosti π
π . . . relativní četnost
jednotek s vlastností A v populaci
π
p
p . . . relativní
četnost jednotek s vlastností A ve výběru
výběry s opakováním → binomické rozdělení
výběry bez opakování → hypergeometrické r.
velký výběrový soubor – aproximace normálním rozdělením
Слайд 25Předpoklad: velký rozsah výběru
interval spolehlivosti
pro populační relativní četnost π
p
. . . výběrová relativní četnost
uα . . . kritická
hodnota normálního rozdělení pro hladinu významnosti αСлайд 26Příklad
V náhodném výběru 400 studentů je 88 leváků. Zkonstruujte 95%
interval spolehlivosti pro podíl leváků v populaci.
Слайд 27Neparametrický odhad mediánu
citlivost aritmetického průměru na vybočující
hodnoty, důležité zvláště u malých souborů
medián – robustní charakteristika
polohy - výběrový medián
M – populační medián
Intervalový odhad populačního mediánu M
Předpoklad: spojitost znaku X
Слайд 28P(xk ≤ M ≤ xn-k+1) ≥ 1 - α
Příklad: u
skupiny 15 náhodně vybraných osob byl zjišťován čistý měsíční příjem
(v tis. Kč), sestrojte95% interval spolehlivosti pro populační medián.
15, 16, 19, 21, 21, 22, 23, 24, 25, 25, 26, 26, 27, 27, 28
data uspořádaná od min po max
podle rozsahu výběru n se nalezne takové přirozené číslo k , pro které