Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Стационарные задачи квантовой механики
Содержание
- 1. Стационарные задачи квантовой механики
- 2. Волновое уравнение Шредингера Макс Борн
- 3. Примеры операторов для одномерного движения частиц
- 4. Стационарные состояния
- 5. Свойства волновой функции
- 6. Свойства волновой функции (продолжение)
- 7. Частица в одномерной потенциальной яме с непроницаемыми стенкамиСтационарные задачи квантовой механики1
- 8. Слайд 8
- 9. Слайд 9
- 10. Движение частицы в области прямоугольной потенциальной ступеньки. .2
- 11. Квантовая частица способна проникать в область, запрещенную классической механикой.
- 12. Слайд 12
- 13. На рис.3 представлена зависимость плотности вероятности обнаружения частицы от координаты xдля отраженной и прошедшей волн.
- 14. Слайд 14
- 15. С точки зрения
- 16. Слайд 16
- 17. Прямоугольный потенциальный барьер. Туннельный эффект. 3
- 18. Слайд 18
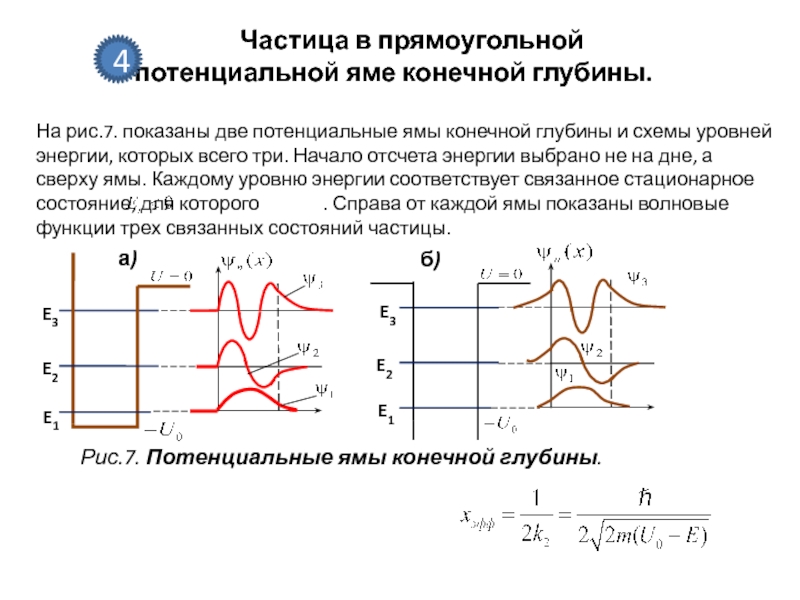
- 19. Частица в прямоугольной потенциальной яме конечной глубины. 4
- 20. Слайд 20
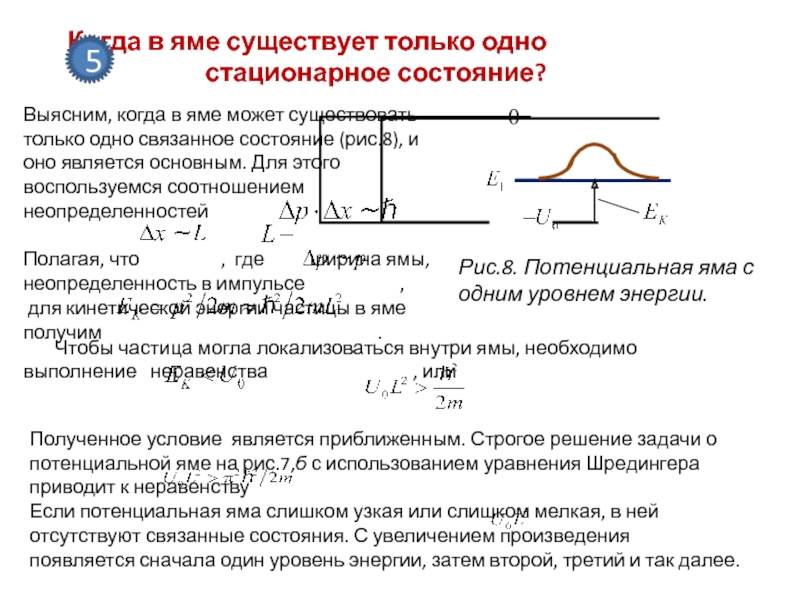
- 21. Когда в яме существует только одно стационарное состояние?5
- 22. Выводы: 6
- 23. Квантовый гармонический осциллятор.
- 24. Квантово-механическая задача о гармоническом осцилляторе сводится к
- 25. Слайд 25
- 26. Слайд 26
- 27. Из приведенного рассмотрения следует:
- 28. 4.
- 29. Слайд 29
- 30. Нулевые колебания
- 31. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Стационарные задачи квантовой механики
Стационарные квантовые состояния
Свойства
волновой функции
Одномерная
потенциальная яма
Прямоугольная
Слайд 2Волновое уравнение Шредингера
Макс Борн и другие
исследователи сформулировали постулат, утверждающий, что каждой физической величине соответствует математический
оператор, обладающий определенными свойствами.Соотношения между операторами имеет ту же структуру, что и соотношения между физическими величинами в классической механике.
Например, уравнение Шредингера можно записать в символическом (операторном)
виде как
Операторы физических величин.
(Операторы обозначены «шляпками»)
Слайд 3Примеры операторов для одномерного движения частиц
Под оператором
понимают математическое правило по которому одна функция
преобразуется в другую
(оператор дифференцирования, оператор умножения, и др.).В формулах оператор действует на функцию, стоящую справа от него.
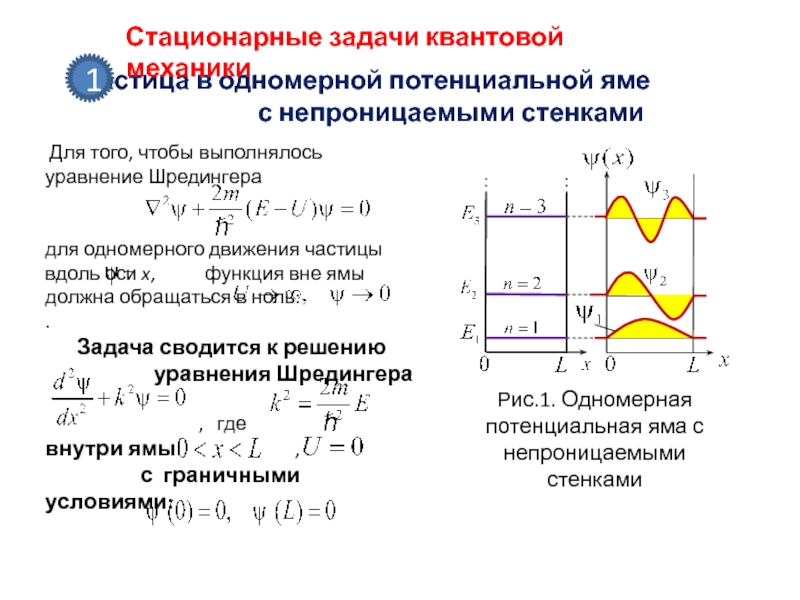
Слайд 7Частица в одномерной потенциальной яме с непроницаемыми стенками
Стационарные задачи квантовой
механики
1
Слайд 13На рис.3 представлена
зависимость плотности вероятности обнаружения частицы от координаты
x
для отраженной и прошедшей волн.
Слайд 15 С точки зрения классической механики ни
одна частица в этом случае не будет отражаться от скачка
потенциальной энергии в точке x = 0.Слайд 23
Квантовый гармонический осциллятор.
Гармонический осциллятор – это система,
способная совершать гармонические колебания. Малые колебания
вблизи положения равновесия можно считать гармоническими.Примером таких колебаний в квантовой механике являются колебания атомов в молекулах, твердых телах и т.д.
7
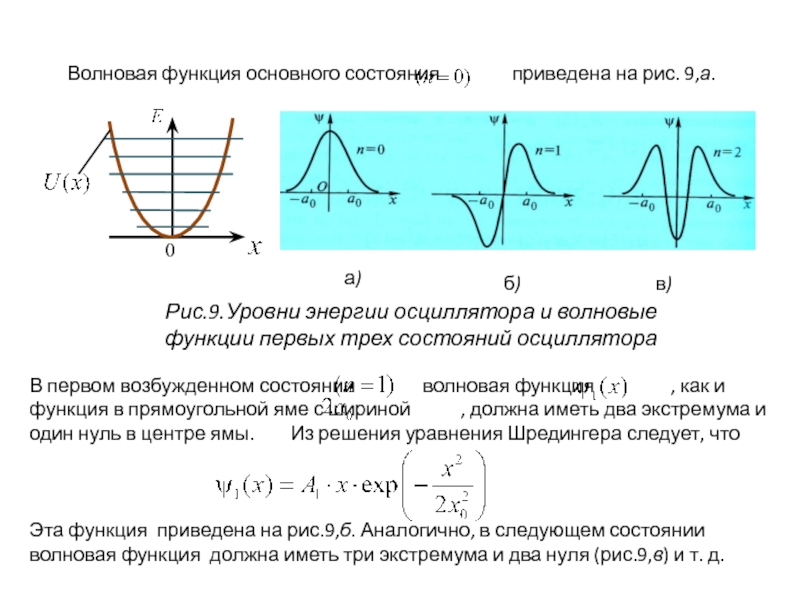
Слайд 24Квантово-механическая задача о гармоническом осцилляторе сводится к задаче о движении
частицы в параболической потенциальной яме и решению стационарного уравнения Шредингера
Слайд 28 4. Представим себе, что
между параллельными металлическими экранами, перпендикулярно им, образовалась электромагнитная стоячая волна.
В такой волне происходят колебания электрического и магнитного поля – это тоже осциллятор. Обобщенной координатой можно считать напряженность электрического поля в какой-либо точке.В качестве импульса должна быть величина, пропорциональная скорости изменения электрического поля. Такой величиной является магнитное поле. При выборе таких обобщенных величин энергия будет иметь такой же вид записи, как у осциллятора. К стоячей волне – осциллятору можно применить уже известные результаты квантования.
Слайд 30Нулевые колебания
В основном состоянии,
состоянии с минимальной энергией, происходят нулевые колебания. Можно найти вероятность
того или иного значения электрического или магнитного поля. Средний квадрат напряженности электрического и средний квадрат напряженности магнитного полей имеют неравные нулю значения, даже если в пространстве нет ни одной частицы и ни одного фотона электромагнитного поля. Фотоны возникают как возбужденные состояния этого поля. Существуют нулевые колебания в вакууме всех возможных физических полей в основном состоянии, колебания, состоящие в появлении и исчезновении электрон-позитронных, нуклон-антинуклонных и других пар. С этой точки зрения вакуум наполнен такими не родившимися, образующимися и исчезающими частицами. Они называются виртуальными частицами. Достаточно возбудить вакуум, сталкивая, например, два нуклона, виртуальные частицы могут превратиться в реальные – при столкновении рождаются новые частицы.
9