Структуры и алгоритмы обработки данных на ЭВМ Алгоритм Дейкстры

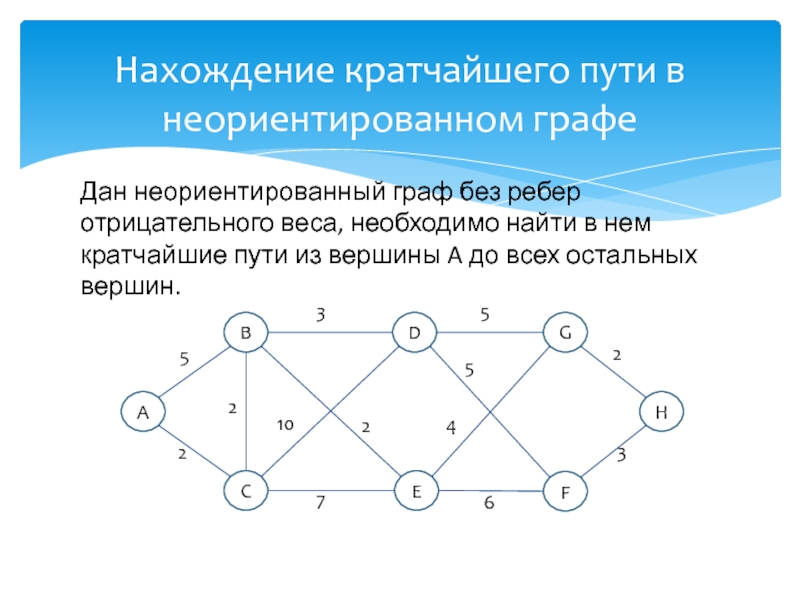
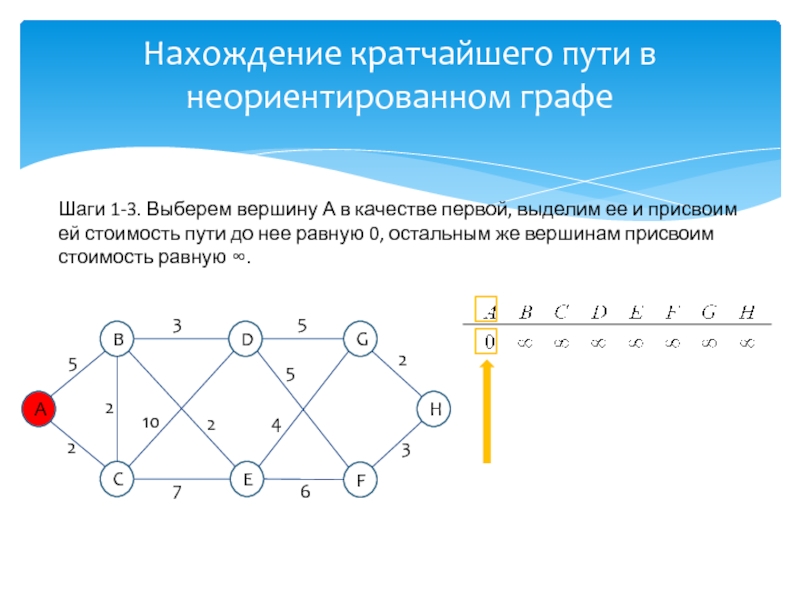
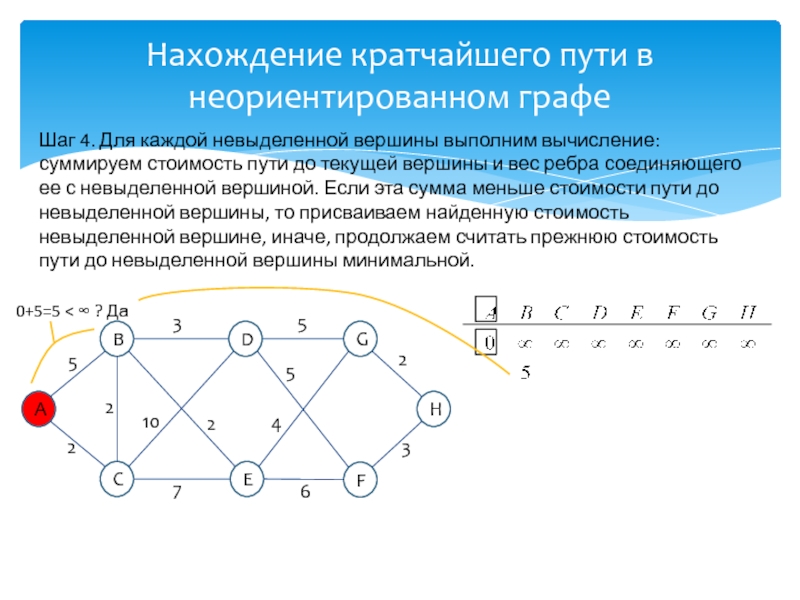
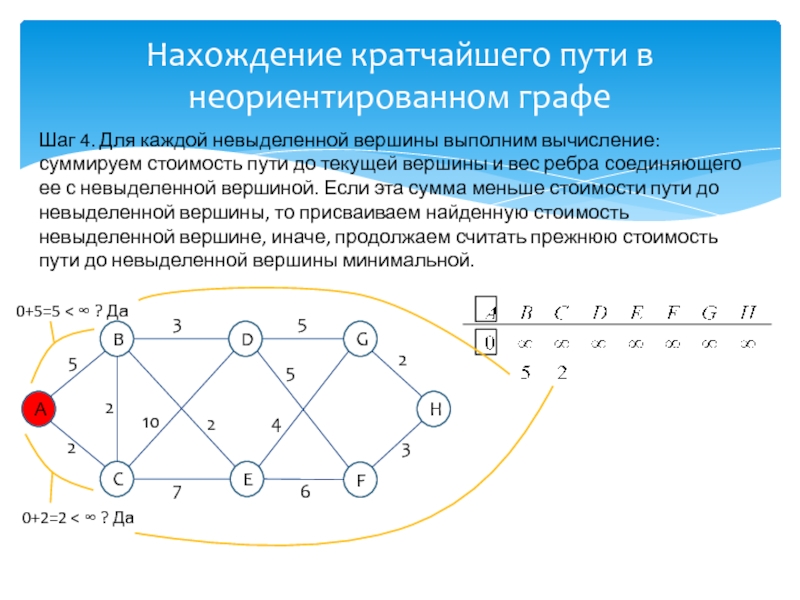
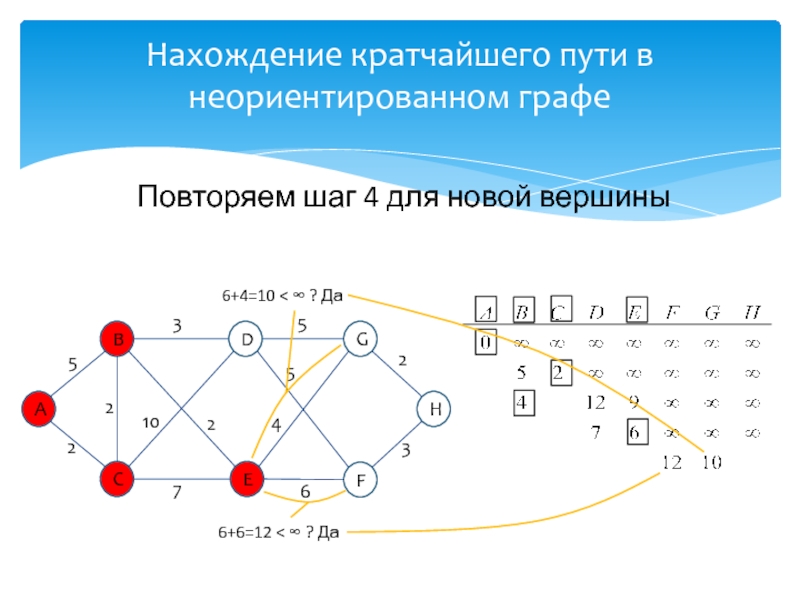
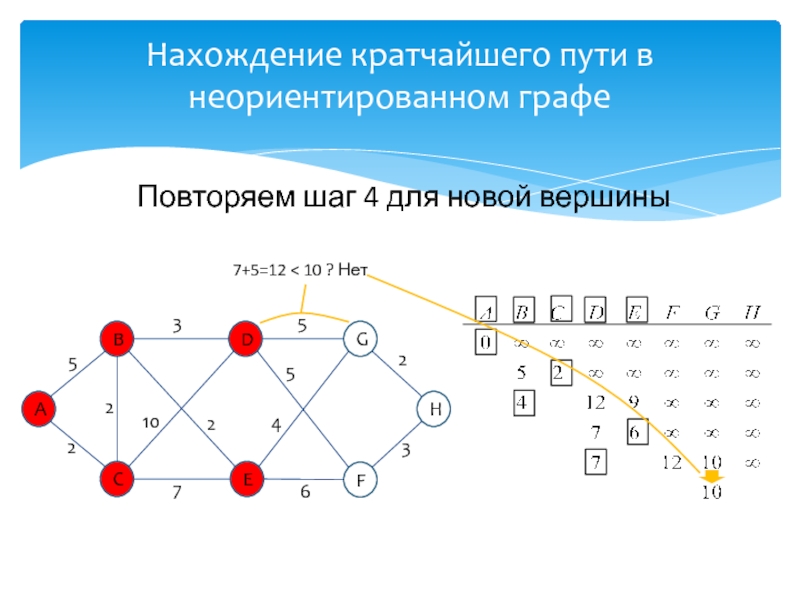
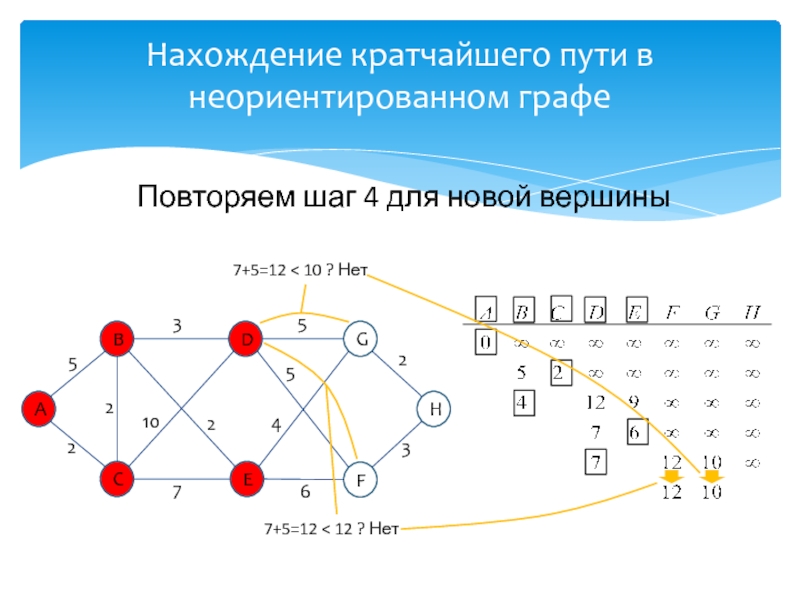
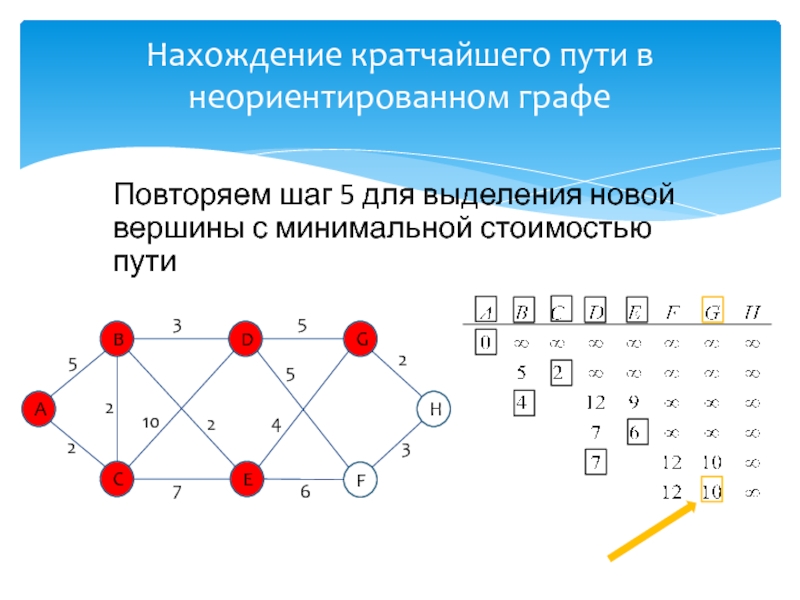
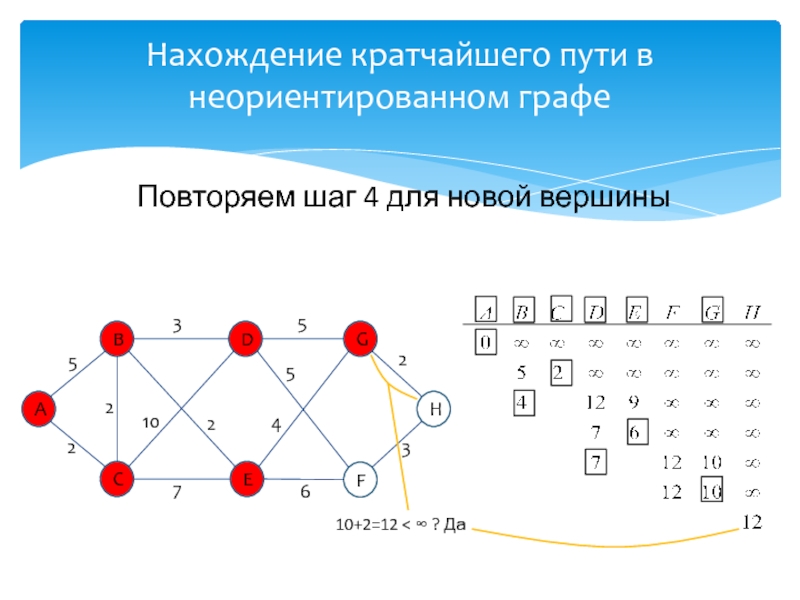
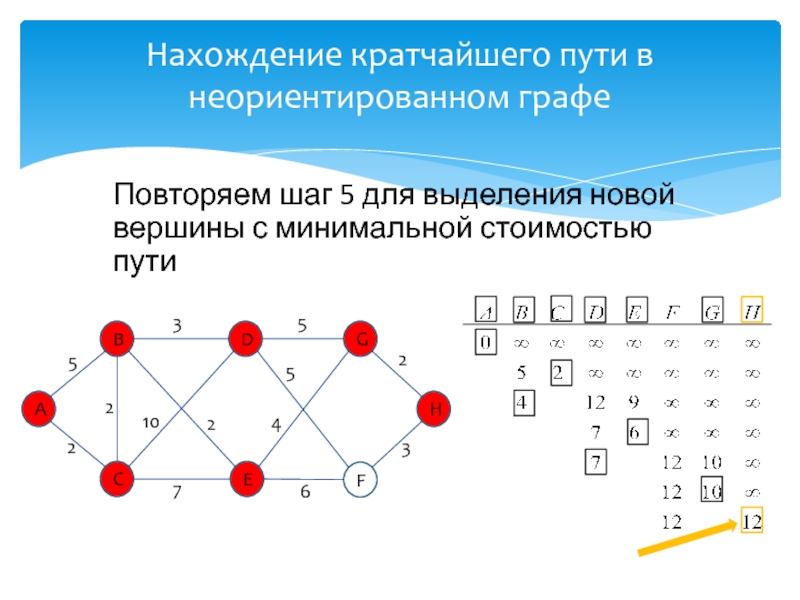
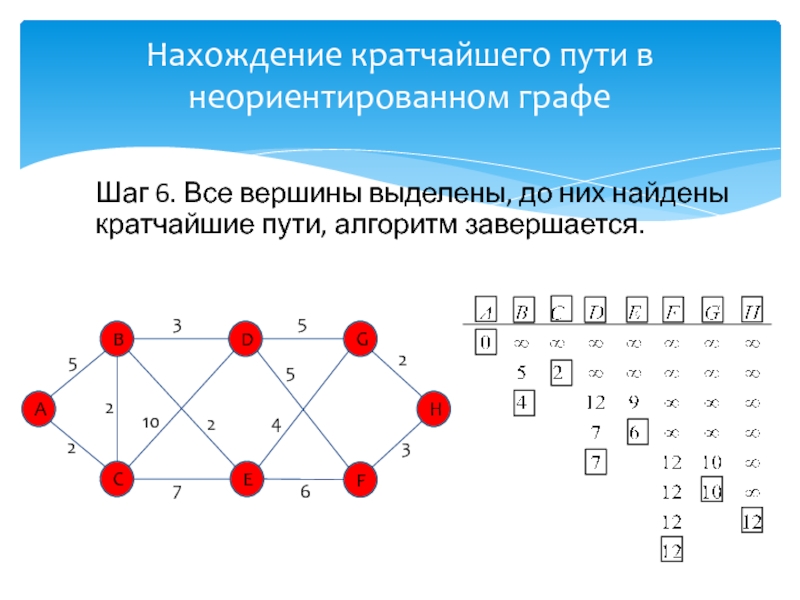
развитие информатики и информационных технологий, является одним из разработчиков концепции структурного программирования и других

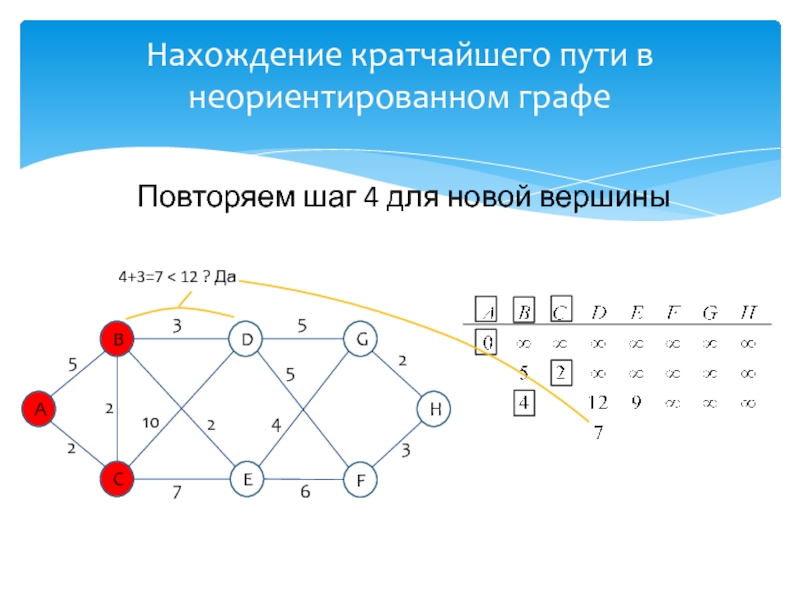
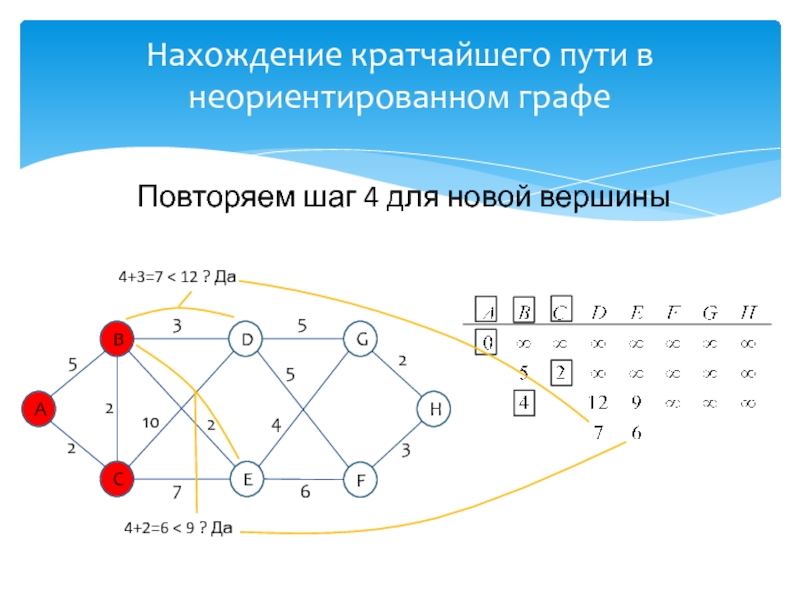
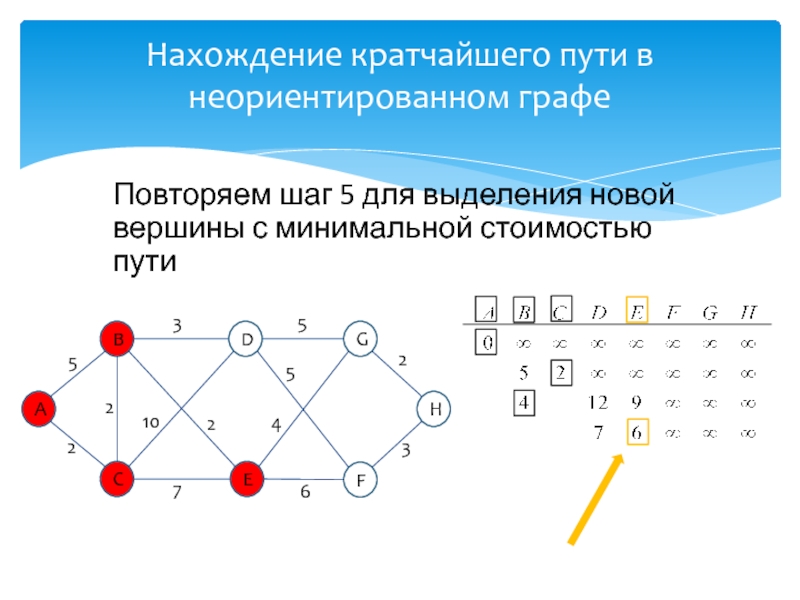
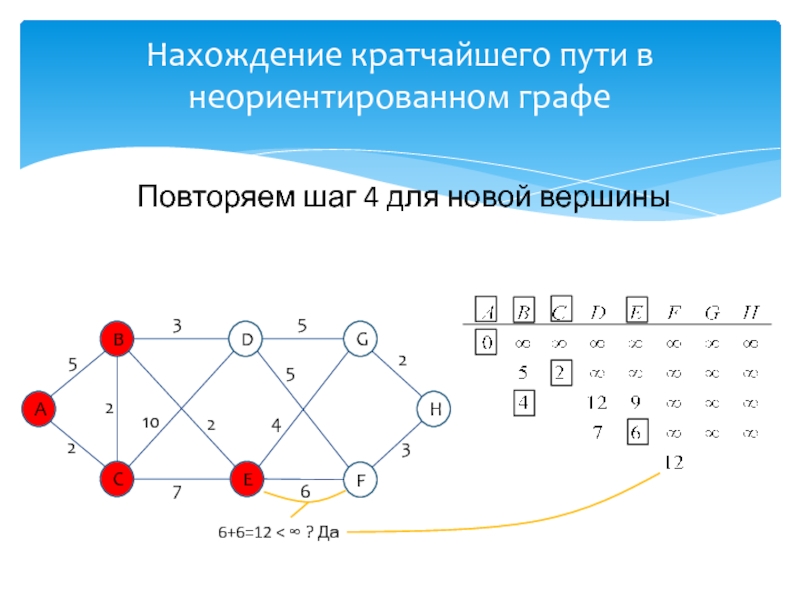
идей,  лауреат премии Тьюринга 1972г.
Известность Дейкстре принесли его работы в области применения математической логики при разработке компьютерных программ, идея применения «семафоров» для синхронизации процессов в многозадачных системах, а так же разработка алгоритма нахождения кратчайшего пути на взвешенном графе без ребер отрицательного веса.

Введение

кратчайшего пути в графе.

Задачи

остальным вершинам ∞;
Все вершины являются не выделенными;
Объявить первую вершину текущей;
Стоимости

путей до всех невыделенных вершин находятся след. образом: стоимость пути до невыделенной вершины есть минимальное число из стоимости старого пути до данной вершины, равное сумме стоимости пути до текущей вершины и веса ребра соединяющего текущую и невыделенную вершины.
Среди невыделенных вершин выбирается вершина с минимальной стоимостью пути до нее. Если такой вершины нет (стоимость путей до всех вершин равна ∞), то путь не существует и алгоритм завершается, иначе текущей вершиной становится найденная, и она же выделяется.
Если все вершины являются выделенными (до всех них найден кратчайший путь), то алгоритм завершается, иначе переход на шаг 4.

Последовательность шагов

отрицательного веса, необходимо найти в нем кратчайшие пути из вершины

A до всех остальных вершин.

А в качестве первой, выделим ее и присвоим ей стоимость

пути до нее равную 0, остальным же вершинам присвоим стоимость равную ∞.

невыделенной вершины выполним вычисление: суммируем стоимость пути до текущей вершины

и вес ребра соединяющего ее с невыделенной вершиной. Если эта сумма меньше стоимости пути до невыделенной вершины, то присваиваем найденную стоимость невыделенной вершине, иначе, продолжаем считать прежнюю стоимость пути до невыделенной вершины минимальной.

0+5=5 < ∞ ? Да

невыделенной вершины выполним вычисление: суммируем стоимость пути до текущей вершины

и вес ребра соединяющего ее с невыделенной вершиной. Если эта сумма меньше стоимости пути до невыделенной вершины, то присваиваем найденную стоимость невыделенной вершине, иначе, продолжаем считать прежнюю стоимость пути до невыделенной вершины минимальной.

0+5=5 < ∞ ? Да

0+2=2 < ∞ ? Да

вершин выбирается вершина с минимальной стоимостью пути до нее. Если

такой вершины нет (стоимость путей до всех вершин равна ∞), то путь не существует и алгоритм завершается, иначе текущей вершиной становится найденная, и она же выделяется

Да
Шаг 4. Для каждой невыделенной вершины выполним вычисление: суммируем стоимость

пути до текущей вершины и вес ребра соединяющего ее с невыделенной вершиной. Если эта сумма меньше стоимости пути до невыделенной вершины, то присваиваем найденную стоимость невыделенной вершине, иначе, продолжаем считать прежнюю стоимость пути до невыделенной вершины минимальной.

Да
Повторяем шаг 4 для новой вершины
2+10=12 < ∞ ? Да

Да
Повторяем шаг 4 для новой вершины
2+10=12 < ∞ ? Да
2+7=9

< ∞ ? Да

выделения новой вершины с минимальной стоимостью пути

новой вершины
4+3=7 < 12 ? Да

новой вершины
4+3=7 < 12 ? Да
4+2=6 < 9 ? Да

выделения новой вершины с минимальной стоимостью пути

новой вершины
6+6=12 < ∞ ? Да

новой вершины
6+6=12 < ∞ ? Да
6+4=10 < ∞ ? Да

выделения новой вершины с минимальной стоимостью пути

новой вершины
7+5=12 < 10 ? Нет

новой вершины
7+5=12 < 10 ? Нет
7+5=12 < 12 ? Нет

выделения новой вершины с минимальной стоимостью пути

новой вершины
10+2=12 < ∞ ? Да

выделения новой вершины с минимальной стоимостью пути

новой вершины
12+3=15 < 12 ? Нет

выделены, до них найдены кратчайшие пути, алгоритм завершается.

= 0;
A → B = 4;
A → C = 2;
A

→ D = 7;
A → E = 6;
A → F = 12;
A → G = 10;
A → H = 12;