Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сведения из теории сложности
Содержание
- 1. Сведения из теории сложности
- 2. Оценка стойкостикриптоанализ современных систем шифрования сводится к
- 3. Для существующих систем неизвестны наилучшие возможные
- 4. Теория сложности Простые алгоритмыАлгоритмы, требуемое число операций для
- 5. Теория сложностиСложные алгоритмыАлгоритмы, требуемое число операций для решения которых, зависит экспоненциально от размерности задачиT~abnEXPTIME задачи
- 6. Теория сложностиNP – задачи(Недетерминировано-полиномиальные)Это задачи для которыхрешение требует экспоненциального числа шаговПроверка решения требует полиномиального числа шагов
- 7. Задача о пути коммивояжераНахождение гамильтонова цикла на графе
- 8. NPC – задачиЕсли для какой-либо NPC задачи
- 9. Теория сложностиПодходы к оценки сложностиПри оценке сложности
- 10. Типы алгоритмов:«обычные» алгоритмы (дают точный правильный ответ).рандомизированные
- 11. Выбор задач для системыКриптосистемы строят так, чтобы
- 12. Оценка стойкостиПри оценки стойкости исходятиз наилучших известных
- 13. Методы защиты данныхПринцип шифрования:Блоковые шифры(Блочные)Потоковые шифры(Поточные)
- 14. Маскираторы аналоговых сообщенийЗащита аналоговой (обычно речевой) информации без преобразования в цифровую форму
- 15. Маскираторы аналоговых сообщенийПреобразование (перестановка частотных полос)fS(f)fS(f)
- 16. Маскираторы аналоговых сообщенийПреобразование (инверсия в полосе частот)fS(f)fS(f)
- 17. Маскираторы аналоговых сообщенийПреобразование задержка сигнала в полосе
- 18. Особенности маскираторовДостоинстваРаботают в реальном времениОтносительно простые и
- 19. Особенности маскираторовНедостаткиСильно падает качество сигнала:Особенно при слишком
- 20. Особенности маскираторовДля надежной защиты речевых сигналов их
- 21. Блоковые шифрыПри шифровании сообщение разбивается на части
- 22. Шеннон 1949г – основные принципы построения стойких
- 23. Блоковые шифры1010000100101010000010010100000110101110001111000011000001011101011110001010101111100101 Нелинейное преобразованиеШифр замены (зависит от ключа)2 ПеремешиваниеШифр перестановки3Многократное повторение
- 24. Шифр заменыЦель – обеспечить сложную взаимосвязь между
- 25. Шифр перестановкиЦель – устранить устойчивые сочетания символов
- 26. Многократное повторениеЦель – устранение недостатка каждого отдельного
- 27. Потоковые шифрыШифрование производится посимвольно. Ключ меняется от символа к символуE=M+K - шифрованиеM=E+K - расшифрование
- 28. Потоковый шифр KMEKEMОткрытый канал связиСекретный канал связиK
- 29. Потоковый шифрФормирование ключаФормирование из короткого секрета длинной
- 30. Потоковый шифрОсобенностиПростая реализация (дешевые)Высокая скоростьНе вносит задержек
- 31. Блоковые шифрыПримеры блоковых шифров и параметров (длина
- 32. Блоковые шифрыИспользуются для шифрования файлов на дисках и т.п., когда не критичны задержки …Потенциально надежнее потоковых
- 33. Блоковые шифрыЗащита от модификации1-й сеанс2-й сеансЗащита – при шифровании взаимосвязь блоковABE1E2E3E4ABE5E6E7E8XXE3
- 34. Потоковый шифрИспользуется для защиты данных в линиях
- 35. A5
- 36. Криптосистемы с открытым ключомКш = КрКш обозначим
- 37. Сравнение систем (см. рис): a) с открытым ключом б) традиционныеФормирование ключейРаспределение ключейШифрованиеПередача EРасшифрование
- 38. Упрощение распределения ключейЗащита от подмены
- 39. Вычисления по модулю1+1 mod 2 =02+3 mod
- 40. RSAКлючи шифрованияK – открытый ключ k – секретный ключN – модуль шифрованияШифрованиеE=MK mod NРасшифрованиеM=Ek mod N
- 41. Цифровая подписьОбычный документПодлинность:Физическая целостностьУникальные характеристики росписиСвязь
- 42. Цифровая подписьПрямой перевод (сканирование) подписанного документа в
- 43. Скачать презентанцию
Оценка стойкостикриптоанализ современных систем шифрования сводится к решению какой-либо сложной задачи.Проблема – определения конкретной сложности решения таких задач
Слайды и текст этой презентации
Слайд 2Оценка стойкости
криптоанализ современных систем шифрования сводится к решению какой-либо сложной
задачи.
Слайд 3
Для существующих систем неизвестны наилучшие возможные алгоритмы решения
Т.е. есть общеизвестные
методы решения, но неизвестно – нет ли более эффективных.
Более эффективных
систем никто не нашел, но никто и не доказал, что их не существуетОценка стойкости
Слайд 4Теория сложности
Простые алгоритмы
Алгоритмы, требуемое число операций для решения которых, зависит
полиномиально от размерности задачи
T~anb
Размерность задачи (n)
Количество неизвестных в системе
Длина
ключаСлайд 5Теория сложности
Сложные алгоритмы
Алгоритмы, требуемое число операций для решения которых, зависит
экспоненциально от размерности задачи
T~abn
EXPTIME задачи
Слайд 6Теория сложности
NP – задачи
(Недетерминировано-полиномиальные)
Это задачи для которых
решение требует экспоненциального числа
шагов
Проверка решения требует полиномиального числа шагов
Слайд 8NPC – задачи
Если для какой-либо NPC задачи будет найдено решения
полиномиальной сложности, это докажет, что простые решения существуют для всех
NP задачNPC
NP
Слайд 9Теория сложности
Подходы к оценки сложности
При оценке сложности в криптографии задачи
рассматриваются при наилучших параметрах для крипоаналитика
В теории сложности сложность определяется
в общем случае, т.е. по наихудших для решения условияхТ.е. Не все задачи из теории сложности напрямую подходят к криптографии.
Слайд 10Типы алгоритмов:
«обычные» алгоритмы (дают точный правильный ответ).
рандомизированные алгоритмы (случайные) –
дают правильный ответ с некоторой вероятностью.
При вероятности правильного
ответа близкой к 1, с практической точки зрения, рандомизированные алгоритмы не хуже обычных.Слайд 11Выбор задач для системы
Криптосистемы строят так, чтобы наилучший алгоритм криптоанализа
сводился к решению какой-либо NPC-задачи и не имел рандомизированного алгоритма
решенияСлайд 12Оценка стойкости
При оценки стойкости исходят
из наилучших известных алгоритмов решения;
из постоянного
развития быстродействия средств вычислительной техники.
Обычно при проектировании в параметры закладывается
значительный запас.Слайд 14Маскираторы аналоговых сообщений
Защита аналоговой (обычно речевой) информации без преобразования в
цифровую форму
Слайд 17Маскираторы аналоговых сообщений
Преобразование задержка сигнала в полосе частот
Комбинация перечисленных преобразований
Конкретный
вид преобразования определяется ключом, который можно менять для сеансов связи
Слайд 18Особенности маскираторов
Достоинства
Работают в реальном времени
Относительно простые и дешевые
(не требуется ЦАП
АЦП)
На слух преобразованный сигнал воспринимается как шум.
Слайд 19Особенности маскираторов
Недостатки
Сильно падает качество сигнала:
Особенно при слишком сложных преобразованиях и
при ретрансляции сигнала
Не обеспечивают надежной защиты речевого сигнала
При наличии соответствующего
оборудования сообщение вскрывается практически в реальном времени независимо от сложности преобразований из-за большой избыточности речевых сигналов.Слайд 20Особенности маскираторов
Для надежной защиты речевых сигналов их необходимо преобразовывать в
цифровое представление и шифровать.
Такое преобразование приводит к расширению спектра сигнала
– требует сжатияВокодеры
Современные методы сжатия речевых сигналов
Слайд 21Блоковые шифры
При шифровании сообщение разбивается на части (блоки) – каждый
блок преобразуется в блок криптограммы, по одинаковому правилу, определяемому ключом.
Ключ для всех блоков одинаков.Слайд 22Шеннон 1949г – основные принципы построения стойких блоковых шифров.
Идея в
чередовании шифров замены и шифров перестановки и их многократного применения
Например,
ключ может определять какой тип шифра на каком шаге используетсяСлайд 23Блоковые шифры
10100001001010100000100101000
00110101110001111000011000001
01110101111000101010111110010
1 Нелинейное преобразование
Шифр замены (зависит от ключа)
2 Перемешивание
Шифр перестановки
3
Многократное
повторение
Слайд 24Шифр замены
Цель – обеспечить сложную взаимосвязь между символами сообщения и
ключа
(распространить влияние каждого символа сообщения/ключа на все символы криптограммы)
001110101000010100010000101111100110
M:
111010011101010111100001110101011100
E:
1
101000101011001110001100011001101100
Слайд 25Шифр перестановки
Цель – устранить устойчивые сочетания символов в исходном сообщении.
Какие-то
сочетания встречаются чаще и могут при замене заменяться вместе, т.е.
без перестановки в криптограмме какие-то последовательности будут чаще других100010001 – будет чаще.
100010000 – будет реже
Слайд 26Многократное повторение
Цель – устранение недостатка каждого отдельного взятого шага шифрования
Неудачная
замена
(сложно выбрать правильную замену с учетом необходимости обратного преобразования)
Неполное устранение
устойчивых сочетаний при перемешиванииСлайд 27Потоковые шифры
Шифрование производится посимвольно. Ключ меняется от символа к символу
E=M+K
- шифрование
M=E+K - расшифрование
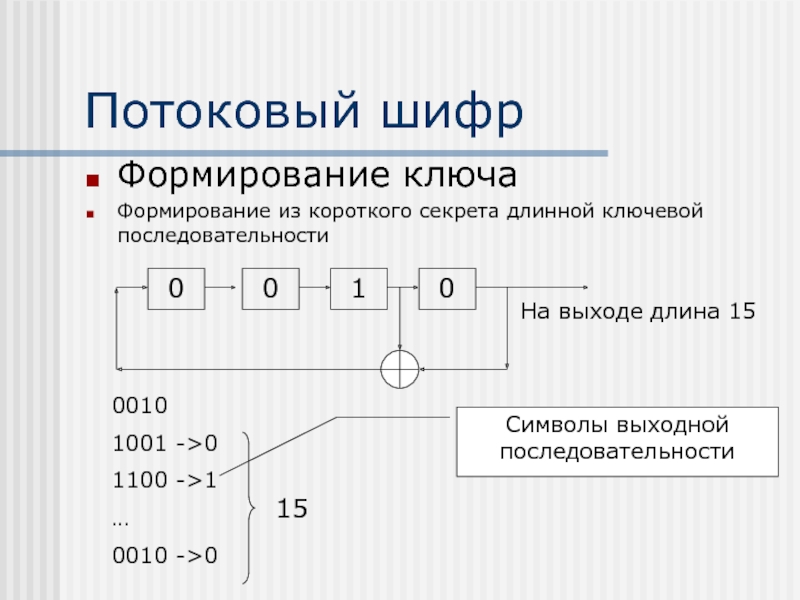
Слайд 29Потоковый шифр
Формирование ключа
Формирование из короткого секрета длинной ключевой последовательности
0
0
1
0
0010
1001 ->0
1100
->1
…
0010 ->0
15
Символы выходной последовательности
На выходе длина 15
Слайд 31Блоковые шифры
Примеры блоковых шифров и параметров (длина ключа; длина блока;
кол-во повторений)
DES (56; 64; 16)
ГОСТ 28147-89 (256; 64; 32)
AES (128,192,256;
128,192,256; ?)Слайд 32Блоковые шифры
Используются для шифрования файлов на дисках и т.п., когда
не критичны задержки …
Потенциально надежнее потоковых
Слайд 33Блоковые шифры
Защита от модификации
1-й сеанс
2-й сеанс
Защита – при шифровании взаимосвязь
блоков
A
B
E1
E2
E3
E4
A
B
E5
E6
E7
E8
X
X
E3
Слайд 34Потоковый шифр
Используется для защиты данных в линиях связи.
В системе GSM
(защита данных от абонента до базовой станции)
см. картинку
Слайд 36Криптосистемы с открытым ключом
Кш = Кр
Кш обозначим К
Кр обозначим k
Идея
– Зная один ключ K, другой ключ k чрезвычайно трудно
вычислитьK - открытый ключ (ключ шифрования)
k - секретный ключ (ключ расшифрования)
Секретные числа
1
k
K
2
3
Слайд 37Сравнение систем (см. рис):
a) с открытым ключом
б) традиционные
Формирование ключей
Распределение ключей
Шифрование
Передача
E
Расшифрование
Слайд 39Вычисления по модулю
1+1 mod 2 =0
2+3 mod 2 =1
13 mod
10 = 3
5*3 mod 6 = ?
111111111 mod 2=?
123-3 mod
100 =?123423*2344*12312235 mod 10=?
Слайд 40RSA
Ключи шифрования
K – открытый ключ
k – секретный ключ
N –
модуль шифрования
Шифрование
E=MK mod N
Расшифрование
M=Ek mod N
Слайд 41Цифровая подпись
Обычный документ
Подлинность:
Физическая целостность
Уникальные
характеристики росписи
Связь подписи и текста –
обеспечивает носитель сообщения (бумага и т.п.)
Договор №
Роплоплплопрло паолыпалыаоп ылао влапрвлопр
валпр лваопр Ываолп ваолпволаполва авп ап волплываопрл роволп ввп вао а вол вопваолп олвапрволпр п п волп о олп волп волапр фыр ап аапалраолр ыло прваолполва п ааа а воорл впрвап ыво воа ор
Роспись
Слайд 42Цифровая подпись
Прямой перевод (сканирование) подписанного документа в цифровое представление допускает
легкую подделку, так как теряется связь между документом и подписью.
Необходимо
связать подпись с документом:Es=fk(M) – создание подписи
(M Es) – хранение, передача подписанного документа
M=gK(Es) – Проверка подписи – совпадает ли левая часть с правой?
?