Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тақырып: Химиялық термодинамика 5В 072300-Техникалық физика мамандығына
Содержание
- 1. Тақырып: Химиялық термодинамика 5В 072300-Техникалық физика мамандығына
- 2. Ашық және жабық жүйелер және олардың теңдеулеріТермодинамиканың
- 3. Жабық жүйелерде характеристикалық функциялар екі тәуелсіз айнымалылардың
- 4. Әрбір компоненттің мөлшері өзгеруімен байланысты изобаралық потенциалдың
- 5. Химиялық потенциалдың мағынасын ашу үшін әрбір
- 6. Сипаттамалық функциялардың басқалары үшін де олардың толық
- 7. Бұл келтірілген теңдеулер химиялық термодинамикадағы негізгі теңдеулер.
- 8. Әуелде компоненттердің массалары тұрақты, ал күй параметрлері
- 9. Екі түрлі процестер қатарымен өткенде, яғни күй
- 10. Химиялық потенциалдың мәнін сипаттамалық функциялардың туындылары арқылы
- 11. Идеал және реал газдардың химиялық потенциалдарыГаздардың тепе
- 12. Сөйтіп, идеал газдардың химиялық потенциалын анықтайтын теңдеуден
- 13. Бұл теңдеудің оң жағындағы бірнеше мүше алынған
- 14. Скачать презентанцию
Ашық және жабық жүйелер және олардың теңдеулеріТермодинамиканың бірінші және екінші заңында біз жабық жүйелерді қарастырдық. Жабық жүйелер айналадағы ортамен тек энергия алмасу арқылы әрекеттеседі. Жабық жүйелермен қатар ашық жүйелер де болады.
Слайды и текст этой презентации
Слайд 1Ермекова Ж.К.
Еуразиялық ұлттық университеті
Асатана, Қазақстан
2014 жыл
Тақырып: Химиялық термодинамика
5В 072300-Техникалық
физика мамандығына арналған гр.ТФ-21
Слайд 2Ашық және жабық жүйелер және олардың теңдеулері
Термодинамиканың бірінші және екінші
заңында біз жабық жүйелерді қарастырдық. Жабық жүйелер айналадағы ортамен тек
энергия алмасу арқылы әрекеттеседі. Жабық жүйелермен қатар ашық жүйелер де болады. Ашық жүйелерде сыртқы ортамен энергия алмасумен қатар зат алмасу да жүзеге асады. Жүйе сыртқы ортамен зат алмасқанда ондағы заттардың мөлшері өзгеріп отырады.Слайд 3Жабық жүйелерде характеристикалық функциялар екі тәуелсіз айнымалылардың функциясы болса, мысалы,
G=f(P,T), ашық жүйеде бұл екуіне айнымалы n шама – жүйенің
құрамы қосылады. Сөйтіп, мысалы, Гиббс энергиясы үш параметрдің функциясыболады . Мұнда – жүйені құратын i-компоненттердің мөлшерлері (моль саны немесе массалары, немесе компоненттердің мөлшерін беретін басқа шамалар). Гиббс энергиясының өзінің жеке туындылары арқылы жазылатын толық дифференциалын алсақ:
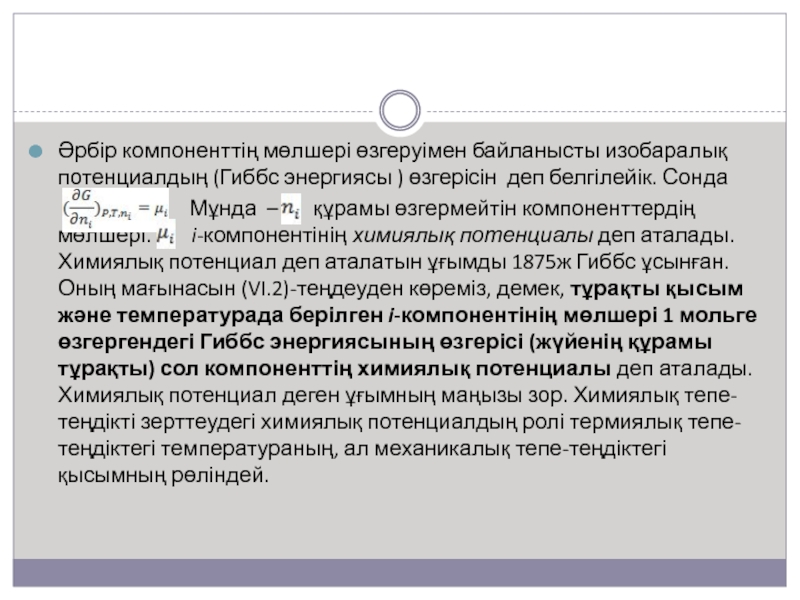
Слайд 4Әрбір компоненттің мөлшері өзгеруімен байланысты изобаралық потенциалдың (Гиббс энергиясы )
өзгерісін деп белгілейік. Сонда
Мұнда – құрамы өзгермейтін компоненттердің мөлшері. i-компонентінің химиялық потенциалы деп аталады. Химиялық потенциал деп аталатын ұғымды 1875ж Гиббс ұсынған. Оның мағынасын (VI.2)-теңдеуден көреміз, демек, тұрақты қысым және температурада берілген i-компонентінің мөлшері 1 мольге өзгергендегі Гиббс энергиясының өзгерісі (жүйенің құрамы тұрақты) сол компоненттің химиялық потенциалы деп аталады. Химиялық потенциал деген ұғымның маңызы зор. Химиялық тепе-теңдікті зерттеудегі химиялық потенциалдың ролі термиялық тепе-теңдіктегі температураның, ал механикалық тепе-теңдіктегі қысымның рөліндей.Слайд 5
Химиялық потенциалдың мағынасын ашу үшін әрбір энергия екі түрлі
параметрдің, яғни экстенсивтік (координата) және интенсивтік (потенциал) факторлардың көбейтіндісіне тең
болатынын еске түсірейік.Гиббс энергиясы
Толық дифференциалы:
Изобаралық потенциал – сипаттамалық функция, демек:
және (VI. 4)
(VI. 5) деп жазуға болады.
Жүйеде зат алмасу процестері өткенде химиялық потенциал интенсивтік фактор болады.
Слайд 6Сипаттамалық функциялардың басқалары үшін де олардың толық дифференциалдары ашық жүйелерде
(VI. 1) – теңдеуге ұқсас теңдеулермен өрнектеледі.
Мысалы, ішкі энергияны алсақ:
– барлық компоненттердің тұрақты болу белгісі. Жүйенің еркін энериясы Жүйенің энтальпиясы:
Бұлардың бәрі сипаттамалық функциялар екенін ескерсек, төмендегі теңдеулерді аламыз:
(VI. 9)
(VI. 9а)
(VI. 9б)
(VI. 9в)
Слайд 7Бұл келтірілген теңдеулер химиялық термодинамикадағы негізгі теңдеулер. Жалпы алғанда жүйеге
берілген жылу ішкі энергия өзгерісіне, ұлғаю жұмысына және басқа күштердің
жұмыс өндірілуіне жұмсалады. Мұндай күштерге химиялық процестердегі күштер де жатады. Жоғарыдағы берілген жаңа шама – химияялық потенциал осы химиялық күштің өлшемі ретінде алынады (- ), ал координата болып компоненттің массасы алынады. Сондахимиялық жұмыс деп саналады. Химиялық потенциал термодинамикалық потенциалдардың масса бойынша алынған туындылары. Осы туындылар теріс таңбамен алынғанда химиялық күштердің ролін атқаратынын және оларды массаның өзгерісіне көбейткенде химиялық жұмысты алуға болатынын дәлелдеуіміз керек.
Бұл жерде тағы да бір проблема пайда болады. Жүйенің күйін сипаттайтын параметрлер: қысым, көлем, температура, тығыздық, концентрация, т.б. Жалпы термодинамика осы күй параметрлерін өзгертетін процестерді қарастырады. Химиялық термодинамикада күй параметрлері өзгеруімен қатар жүйенің массасы және оның құрамы өзгереді. Бұларды өзгертетін процестер де жалпы термодинамиканың теңдеуіне бағынатынын дәлелдеуіміз керек.
Слайд 8Әуелде компоненттердің массалары тұрақты, ал күй параметрлері өзгеретін процестерді қарастырайық.
Мұндай жағдайа алынатын шамаларды бір штрихпен белгілесек, термодинамиканың негізгі теңдеуі
төмендегідей жазылады:(VI.10)
Бұнда – ұлғаю жұмысынан басқа жүйедегі өндірілетін жұмыстардың қосындысы;
– интенсивтік фактор (потенциал); – экстенсивтік фактор (координата). Жүйенің массасы және құрамы өзгеретін процестердегі шамаларды екі штрихпен белгілеп термодинамикалық потенциалдың өрнегін алсақ, мысалы, изобаралық потенциалдың өрнегі: Мұның дифференциалы (P = const, T = const):
(VI.11)
Жүйенің массасы, құрамы өзгергенде изобаралық потенциалдың өзгерісі былай да жазылады (P = const, T = const)
(VI. 12)
Бұл екі теңдеуді теңестірсек: (VI. 13)
Слайд 9Екі түрлі процестер қатарымен өткенде, яғни күй параметрлері өзгеруімен бірге
жүйенің массасы мен құрамы өзгерсе, жоғарыдағы шамалардың жалпы өзгерістері:
(VI. 10)-теңдеу мен (VI. 13)-теңдеуді қосқанда (VI. 14)
Бұл теңдеу жоғарыдағы айтылғандарды дәлелдейді. Сөйтіп, химиялық термодинамиканың теңдеуі (VI. 14)-теңдеу арқылы жазылады, химиялық потенциал теріс таңбамен алынғанда химиялық күштердің ролін атқарады. Энтропияның өзгерісі бұл теңдеуде екі бөліктен құралады: - бөлігі жүйеге берілген жылу арқылы өзгерісі болса, - жылу арқылы да және компоненттердің масса өзгерістері арқылы да өсетін энтропияның бөлігі. Көлемнің және ішкі энергияның өзгерістері осы айтылған сияқты жүйедегі басқа процестермен қосымша жүйенің құрамының өзнерістеріне байланысты.
(VI.9, VI.9a, VI.9б, VI.9в)-теңдеулерді Гиббстің негізгі теңдеулері деп атайды, бұл теңдеулер сипаттамалық функциялар мен олардың айнымалыларының арасындағы байланысты көрсетіп, К – компоненттен тұратын жүйеге толық термодинамикалық қасиеттерін көрсету үшін олардың кез келген біреуі жеткілікті
Слайд 10Химиялық потенциалдың мәнін сипаттамалық функциялардың туындылары арқылы табуға болады. Гиббстің
негізгі теңдеулері бір – біріне эквивалентті болғандықтан мына теңдік орындалады:
(VI. 15)Осы теңдеуден таза заттың химиялық потенциалын табуға болатыны түсінікті. Мысалы, изобаралық потенциалды алсақ заттың химиялық потенциалы осы заттың 1 моліне тиісті Гиббс энергиясының мөлшеріне тең екендігі айқын (a-заты үшін)
Өйткені, таза заттың мөлшері 1 мольге өзгергенде Гиббс энергиясының өзгеруі заттың бір молінің Гиббс энергиясына тең болады.
Тұрақты қысым мен тұрақты температурада (VI. 3) – теңдеудің оң жағындағы екі мүшесі нольге тең болғандықтан оны былайша жазуға болады:
(VI. 16)
Өздігінен өтетін қайтымсыз процестер үшін T = constжәне Р = const жағдайда , сондықтан (VI. 16)-теңдеу бойынша: (VI. 17)
Бұл өрнек ашық жүйелерде орындалады. Жүйенің тепе – теңдік күйінде теңсіздік теңдікке айналады: (VI. 17а)
Тұрақты қысым және тұрақты температурада ашық жүйеде тепе-теңдік орнағанда (VI. 17а) – теңдеу орындалады, яғни ашық жүйенің тепе-теңдік жағдайы компоненттердің химиялық потенциалдарымен анықталады.
Слайд 11Идеал және реал газдардың химиялық потенциалдары
Газдардың тепе – теңдік қасиеттерін
химиялық потенциал арқылы көрсетуге болады.
Тұрақты температурада (VI. 5) –
теңдеу былай жазылады: (VI. 18)Бір моль таза зат үшін болатындықтан: (VI. 19)
Мұны интегралдағанда: (VI. 19a)
Интегралды шешу үшін көлем мен қысым арасындағы байланысты білу қажет. Идеал газдар үшін , сонда 1 моль идеал газдың химиялық потенциалы (VI. 19a)-теңдеуден
Стандартты қысымда стандартты химиялық потенциалға тең, яғни (Р=1атм). Сонда 1 моль газ үшін стандартты жағдайда .
Қысым және дейін өзгергенде (VI. 20)
Льюис реал газдардың химиялық потенциалын анықтаудың жолын ұсынған. Ол үшін идеал газдарға қолданылатын теңдеулер пайдаланылады, бірақ ол теңдеулердегі қысымның орнына фигутивтік f алынады (ағылшын тілінде fugacity - ұшқыштық). Сонда (VI. 19) – теңдеуден:
Мұны интегралдағанда (VI. 21)
– интегралдау тұрақтысы.
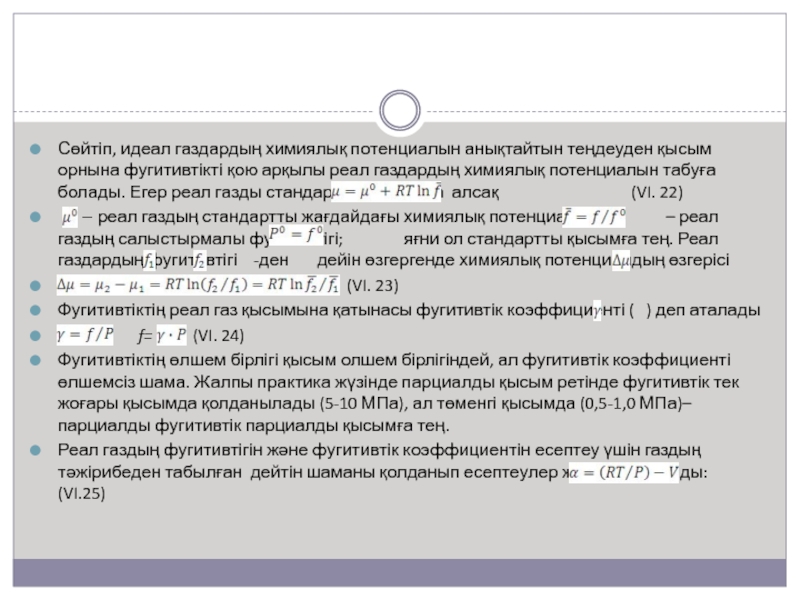
Слайд 12Сөйтіп, идеал газдардың химиялық потенциалын анықтайтын теңдеуден қысым орнына фугитивтікті
қою арқылы реал газдардың химиялық потенциалын табуға болады. Егер реал
газды стандартты жағдайда алсақ (VI. 22)– реал газдың стандартты жағдайдағы химиялық потенциалы; – реал газдың салыстырмалы фугитивтігі; яғни ол стандартты қысымға тең. Реал газдардың фугитивтігі -ден дейін өзгергенде химиялық потенциалдың өзгерісі
(VI. 23)
Фугитивтіктің реал газ қысымына қатынасы фугитивтік коэффициенті ( ) деп аталады
f= (VI. 24)
Фугитивтіктің өлшем бірлігі қысым олшем бірлігіндей, ал фугитивтік коэффициенті өлшемсіз шама. Жалпы практика жүзінде парциалды қысым ретінде фугитивтік тек жоғары қысымда қолданылады (5-10 МПа), ал төменгі қысымда (0,5-1,0 МПа)– парциалды фугитивтік парциалды қысымға тең.
Реал газдың фугитивтігін және фугитивтік коэффициентін есептеу үшін газдың тәжірибеден табылған дейтін шаманы қолданып есептеулер жүргізуге болады: (VI.25)
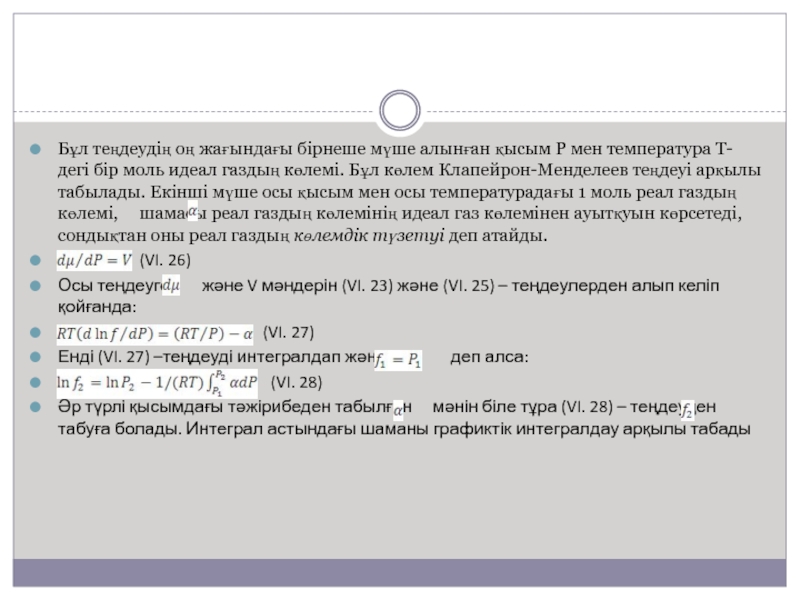
Слайд 13Бұл теңдеудің оң жағындағы бірнеше мүше алынған қысым Р мен
температура Т-дегі бір моль идеал газдың көлемі. Бұл көлем Клапейрон-Менделеев
теңдеуі арқылы табылады. Екінші мүше осы қысым мен осы температурадағы 1 моль реал газдың көлемі, шамасы реал газдың көлемінің идеал газ көлемінен ауытқуын көрсетеді, сондықтан оны реал газдың көлемдік түзетуі деп атайды.(VI. 26)
Осы теңдеуге және V мәндерін (VI. 23) және (VI. 25) – теңдеулерден алып келіп қойғанда:
(VI. 27)
Енді (VI. 27) –теңдеуді интегралдап және деп алса:
(VI. 28)
Әр түрлі қысымдағы тәжірибеден табылған мәнін біле тұра (VI. 28) – теңдеуден табуға болады. Интеграл астындағы шаманы графиктік интегралдау арқылы табады