Тема. 2. Элементы математической логики Высшее назначение математики - находить

Аристотеля.
Прошло два тысячелетия, прежде чем Г. Лейбниц предложил ввести

в логику математическую символику и использовать её для общих логических построений.
Эту идею последовательно реализовал в прошлом столетии Дж. Буль и тем самым заложил основы математической (символической логики).

Тема.2. Элементы математической логики Высшее назначение математики - находить порядок в хаосе, который нас окружает. Н.Винер

Законы булевой алгебры
2.5. Преобразование логических выражений
2.6. Парадоксы математической логики

мысль) является началом любой научной теории. Даже в Библии было

сказано, что "сначала было слово". Логика как наука о способах мышления, приводящих к истине, возникла в глубокой древности. Её основы были заложены древнегреческими философами Перменидом, Зеноном, Протагором, Сократом, сведения о которых дошли до нас благодаря Платону (427-347 гг. до н.э.). Им были также выявлены некоторые принципы и схемы рассуждений.

содержания
рассуждений и создал чистую систему
силлогизмов — правил вывода,

что привело
к возникновению теории логики. Правила
вывода позволяют преобразовывать исход-
ные утверждения подобно тому, как тождес-
твенные преобразования в математике дают возможность решать различные системы уравнений. Последующим шагом формализации логики является появление специальной символики для точной и
компактной записи утверждений и
определения операций над ними.
Идея перенесения тех методов,
которые обычно применяются в
математике, на логику постепенно
реализуется Б. Паскалем (1646-1716),

язык математической логики как логическое продолжение языка математики.

В отличие от объектов реального мира чисто лишены материальной сущности.

Из таких математических объектов можно строить объекты, процессы и явления реального мира. Получаемые при этом подобия называют математическими моделями. Компьютер "оживляет" эти подобия.
С появлением языка математической логики стало возможным составлять алгоритмы логического вывода. Заговорили о создании "искусственного интеллекта", и возник вопрос: «Нельзя ли создать универсальный алгоритм логического вывода (суперинтел-лект), позволяющий доказать или опровергнуть любое утверждение?»

Программа Д.Гильберта была последней попыткой реализации этого универсального алгоритма, но

и она закончилась неудачей. Оказалось, что создание такого суперинтеллекта невозможно даже теоретически.
В 1931 г. австрийский математик Курт Гедель доказал, что всякая достаточно богатая формальная система не полна, то есть в ней найдутся содержательно истинные утверждения, не доказуемые в этой системе. В последние десятилетия логика находит все более широкое применение в технике при исследовании и её методы используются:
в теории преобразования и передачи информации,
теории вероятностей и комбинаторном анализе.
Математическая логика внедрилась в такие нематематические области, как экономика, биология, медицина, психология, языкознание, право.

науки и техники.
Устоявшееся представление о математической логике как науке, изучающей

законы мышления с применением аппарата математики, главным образом, для нужд самой математики, в современных условиях становится слишком узким. С расширением областей применения и дальнейшим развитием математической логики изменяется и взгляд на нее.
Объектами математической логики являются любые дискретные конечные системы, а ее главная задача — структурное моделирование таких систем

и сама усовершенствовалась с помощью этого метода.
Как видно из

предыдущего, название ≪математическая логика≫ может истолковываться двояко.
С одной стороны, эта отрасль науки строится как математическая теория, в ней используются математические методы, так что в этом смысле она представляет собой ≪математику логики≫.
С другой стороны, разрабатывая точный логический язык математики, она служит ≪логикой математики≫.

говорить, что оно истинно или ложно, называется ВЫСКАЗЫВАНИЕМ.
Если высказывание ИСТИННО,

то говорят, что оно принимает значение «И» или «1»,
а если ЛОЖНО, то – «Л» или «0».
Определение 2. Высказывание является ПРОСТЫМ, если никакую его часть нельзя рассматривать как отдельное высказывание.

и т.д.

связок
«НЕ»,
«ИЛИ»,
«И»,
«ЕСЛИ …, ТО …»,
«ТОГДА И

ТОЛЬКО ТОГДА, КОГДА …»
называются СОСТАВНЫМИ или БУЛЕВЫМИ ФУНКЦИЯМИ.
Определение 4. Построение новых высказываний их данных называется ЛОГИЧЕСКИМИ ОПЕРЕЦИЯМИ.

А)), которое считается истинным, если А – ложно, и ложным,

если А – истинно.
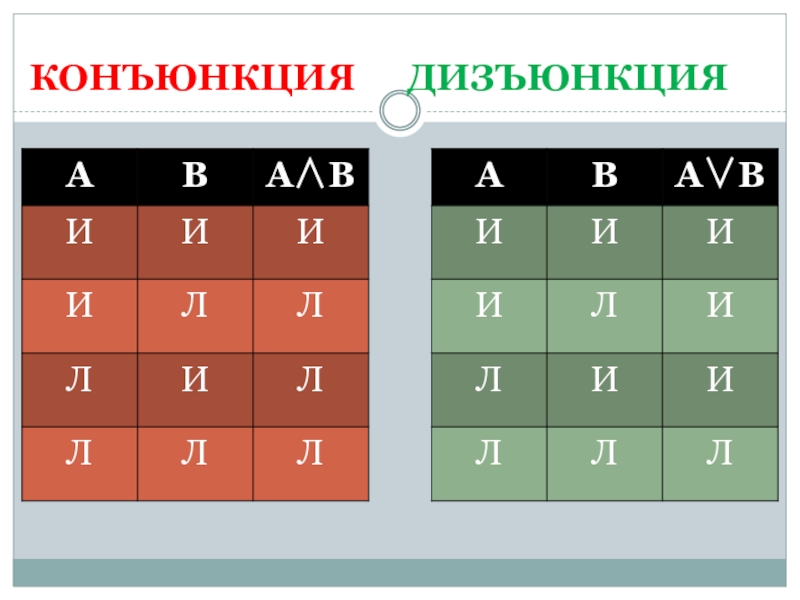
Определение 6. Конъюнкцией двух высказываний А и В называется высказывание («А и В»), которое является истинным, если А и В – истинны, и ложным, если хотя бы одно из них ложно.

(«А или В»), которое является истинным, если хотя бы одно

из них, и ложным, если оба ложны.
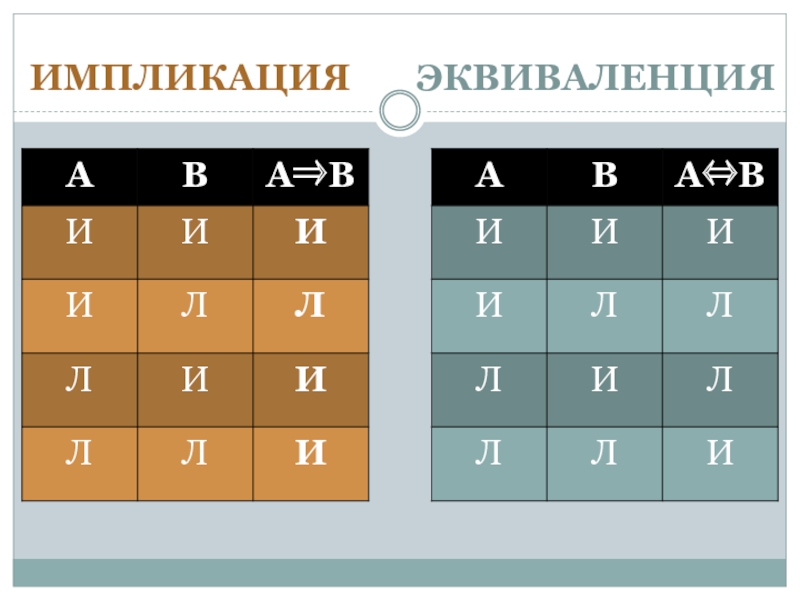
Определение 8. Импликацией двух высказываний А и В называется высказывание («если А, то В»), которое считается ложным, если А истинно и В ложно, и истинным при всех других значениях А и В.

двух высказываний А и В называется высказывание («А эквивалентно В»),

которое является истинным, если оба высказывания А и В одновременно– истинны, либо ложны, и ложным в остальных случаях.
Введенные операции можно описать с помощью таблиц. Эти таблицы называются истинностными таблицами.

переменные по двухэлементному множеству {И, Л}. Тогда сами таблицы задают

двуместные функции следующего типа: {И, Л}2  {И, Л}.
Последняя таблица одноместную функцию типа: {И, Л}  {И, Л}. Эти функции являются операциями на множестве {И, Л}

помощью логических операций
Ф(А1, А2, А3, ..., Аn ).
Определение11. Формулу принимающую

значение «истина» при всех наборах входящих в неё высказываний, называют тождественно-истинной или тавтологией
Ф(А1, А2, А3, ..., Аn ) = 1.

дизъюнкции, которая в свою очередь предшествует импликации и эквиваленции.
Импликация и

эквиваленция выполняются в порядке следования.
При необходимости изменить данную последовательность действий применяются скобки.

методов рассуждений. Изучая эти методы, логика интересуется в первую очередь

формой, а не содержанием доводов в том или ином рассуждении.
Хотя логика и является основой всех остальных наук, тем не менее присущее ей, наряду с фундаментальностью, свойство самоочевидности действовало расхолаживающе на стремление к сколько-нибудь глубоким логическим исследованиям вплоть до девятнадцатого столетия, когда интерес к логике оживился под влиянием открытия неевклидовых геометрий (геометрии Лобачевского), а также необходимости строгого обоснования математического анализа..

века, когда мир был поражен открытием парадоксов, то есть рассуждений,

приводящих к противоречиям. Эти парадоксы обычно называют семантическими.
1. Парадокс лжеца. Некто утверждает: «Я лгу».
Если утверждение истинно, то это в точности означает, что он лжет, т. е. утверждение ложно. Но если утверждение ложно, то это означает, что он говорит правду, то есть его утверждение истинно. В любом случае оно истинно и ложно одновременно.

приказывая при этом брить тех и только тех солдат, которые

не бреются сами. Что же делать брадобрею с самим собою? Если он будет брить себя, то он бреет того, кто бреется сам. Но если он не будет брить себя, то он должен себя побрить. В обоих случаях он должен брить и не брить себя одновременно.
Основная цель математической логики – обеспечить символизм (систему формальных обозначений) для рассуждений, встречающихся не только в математике, но и в повседневной жизни.