Слайд 1Тема 7 Древовидные структуры данных
Понятие древовидной …структуры данных
Бинарное дерево поиска
Слайд 2Понятие древовидной структуры данных
При решении игровых задач мы встретились с
понятием дерева, которое использовалось в качестве математической модели для представления
множества возможных вариантов.
Познакомились с рекурсивным алгоритмом обхода всех узлов и листьев дерева и построенным на нем методом ветвей и границ.
Древовидная модель оказывается довольно эффективной и для представления динамических данных с целью быстрого поиска информации.
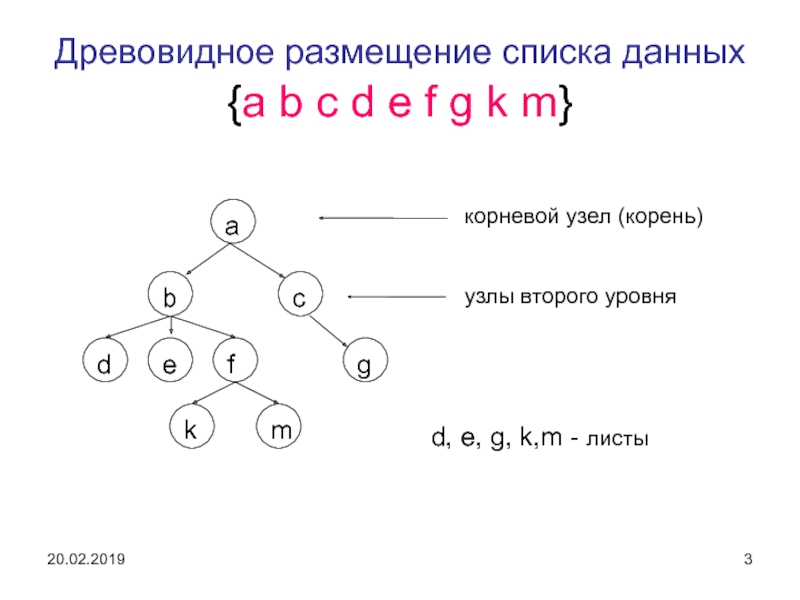
Слайд 3Древовидное размещение списка данных {a b c d e f
g k m}
а
b
c
f
e
d
g
m
k
корневой узел (корень)
узлы второго уровня
d, e, g,
k,m - листы
Слайд 4Основные определения
Если два узла соединены направленной дугой (xy) то
х - предшественник (родитель),
у – преемник (сын, дочь).
Корень - узел, у которого нет родителя.
Лист - Узел, не имеющий преемников
Внутренний узел – это узел, не являющийся листом или корнем.
Порядок узла – количество его дочерних узлов.
Степень дерева – максимальный порядок его узлов
Глубина узла равна числу его предков плюс 1.
Глубина дерева – это наибольшая глубина его узлов.
Дерево, представленное выше имеет степень 3 (троичное), глубину 4, корневой узел а, листы d, e, g, k,m
Слайд 5Для реализации древовидных структур данных степени m используется следующая конструкция
рекурсивного типа данных
Type Ttree=^tree
tree=Record
Inf:TInf;
A1:Ttree;
//A1..Am – указатели
A2:Ttree; //на сестер
... //если сестра
//отсутствует, то
Am:Ttree; //адрес равен Nil
end;
Слайд 6Пример прямого размещения данных
Var proot, p:Ttree;//Указатели: на корень и
текущий узел
...
New(proot); p:=Proot; p^.Inf:=’a’; p^.A2:=Nil;
New(P^.A3); p:=P^.A3; P^.Inf:=’c’;
P^.A1:=Nil;
P^.A2:=Nil; New(P^.A3); p:=P^.A3; p^.Inf:=’g’;
P^.A1:=Nil; p^.A2:=Nil; p^.A3:=Nil; p=Proot;
New(P^.A1); p:=p^.A1; p^.Inf:=’b’; New(P^.A1);
P^.A1.Inf:=’d’; P^.A1^.A1:=Nil; p^.A1^.A2:=Nil;
p^.A1^.A3:=Nil;
New(P^.A2); p^.A2.Inf:=’e’; P^.A2^.A1:=Nil;
P^.A2^.A2:=Nil; p^.A2^.A3:=Nil; New(p^.A3);
p:=P^.A3; p^.Inf:=’f’; p^.A2:=Nil; New(p^.A1);
p^.A1.Inf:=’k’;
P^.A1^.A1:=Nil; p^.A1^.A2:=Nil; p^.A1^.A3:=Nil;
New(p^.A3); p^.A3.Inf:=’m’; P^.A3^.A1:=Nil;
P^.A3^.A2:=Nil; P^.A3^.A3:=Nil
Слайд 7После того как дерево заполнено информацией, его нужно уметь просмотреть,
распечатать, осуществить поиск.
Как видно из вышеприведенного фрагмента программы, непосредственное
заполнение даже небольшого дерева требует довольно громоздкой последовательности команд.
Поэтому для работы с деревьями используют набор специфических алгоритмов, оформленных в виде методов класса.
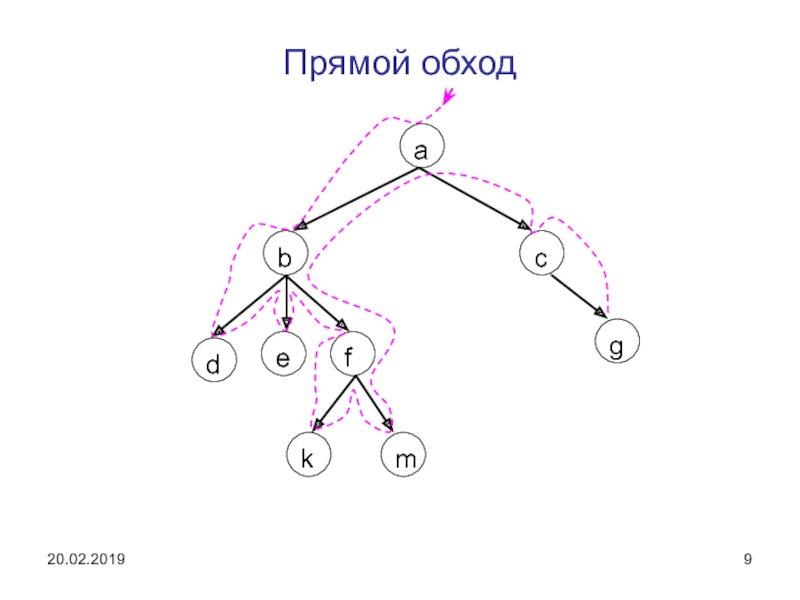
Слайд 8Обходом дерева называется последовательное обращение ко всем его узлам.
Procedure
Wrttree(p:Ttree);
//p - указатель на текущий узел при входе p:=proot
begin
if p<>Nil then //если дочь отсутствует то выход
begin
//печать при прямом обходе
Wrttree(p^.A1);
Wrttree(p^.A2);
...
Wrttree(p^.Am);
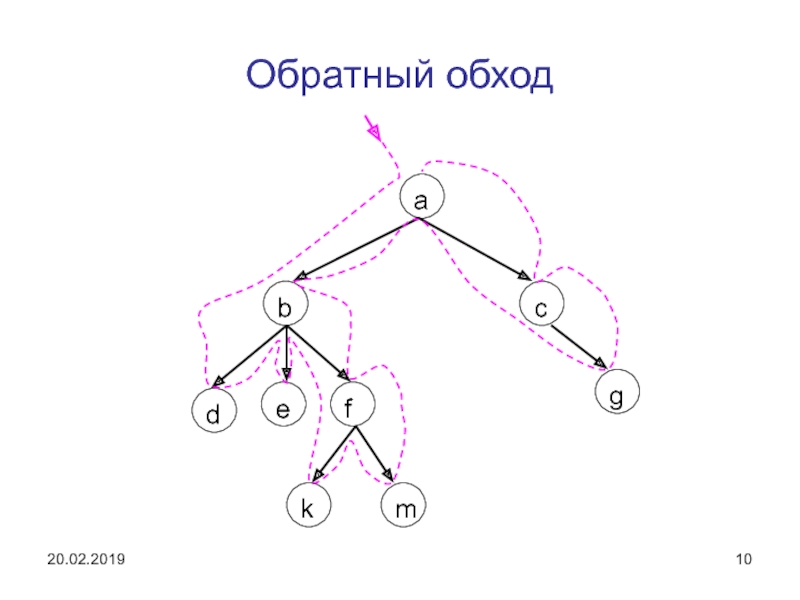
// печать при обратном обходе
end;
end; p:=proot; Wrttree(p);
Слайд 11Var proot,p:Ptree; //
Поиск при обходе
Function Poisktree(k):Tinf
Var bl:boolean;
Procedure Po(var p:Ttree);//обход
Begin
If
bl and (p<>Nil) then
If p^.inf.key=k then bl:=false
else
begin
Po(p.A1);
Po(p.A2);
...
Po(p.Am);
end
end;//Po
begin
p:=proot; bl:=true; Po(p);
If bl then Print(’поиск неудачен’)
else Result:=p^.Inf;
End;//Poisktree
Слайд 12Поиск при обходе
Обращение
Inf:=Poisktree(k);
Слайд 13Удаление дерева из памяти
производится обратным обходом
Procedure DeleteTree(var p:Ttree);
Begin
If (pNil)
then begin
DeleteTree(p^.A1);
DeleteTree(p^.A2);
. . . . .
DeleteTree(p^.Am);
Dispose(p);
p:=Nil;
end;
end;
Обращение: DeleteTree(proot);
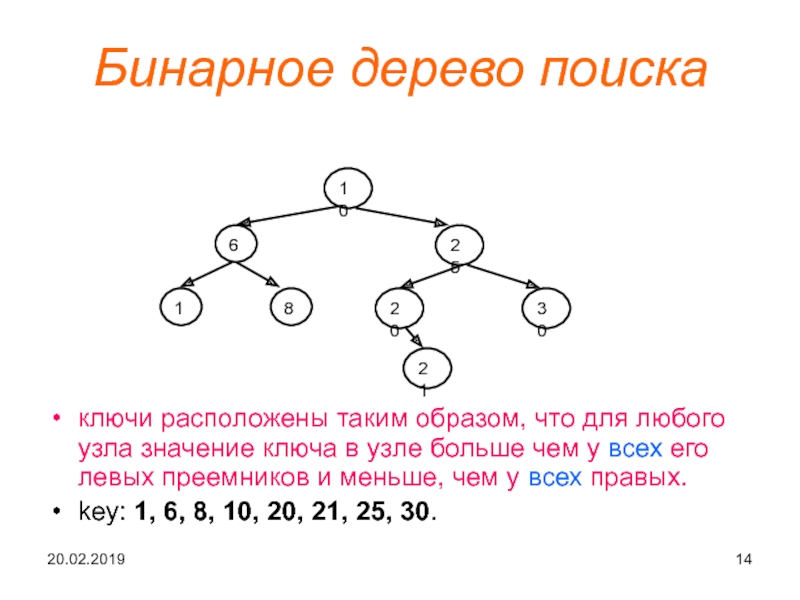
Слайд 14Бинарное дерево поиска
ключи расположены таким образом, что для любого узла
значение ключа в узле больше чем у всех его левых
преемников и меньше, чем у всех правых.
key: 1, 6, 8, 10, 20, 21, 25, 30.
10
25
6
21
30
20
8
1
Слайд 15Ввиду своеобразной организации эффективность поиска информации в такой динамической структуре
данных сравнима с эффективностью двоичного поиска в массиве, т.е. имеет
оценку эффективности О(log2n).
Заметим что двоичный поиск в линейном связанном списке организовать невозможно, а эффективность линейного поиска имеет порядок О(n).
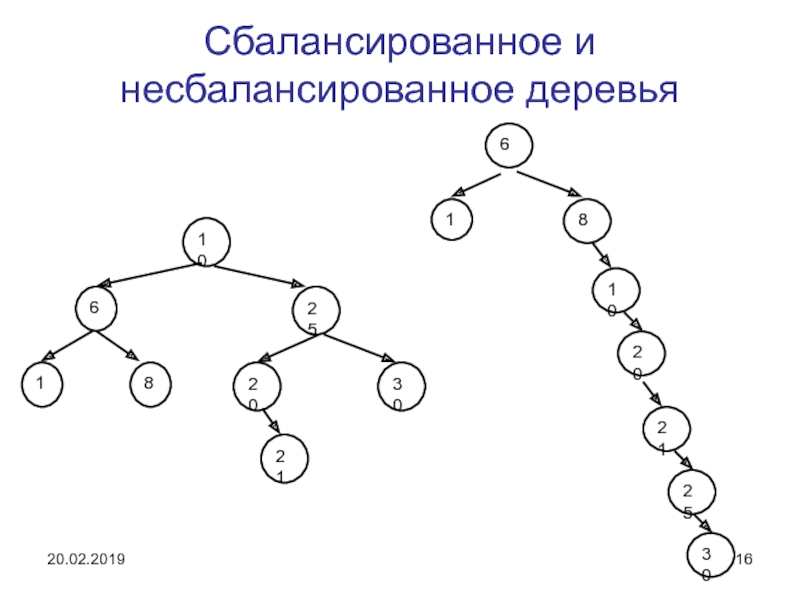
Конечно, оценка О(log2n) справедлива для сбалансированного дерева, т.е. такого у которого узлы, имеющие только одну дочь, имеют глубину равную или на единицу меньшую глубины дерева.
Слайд 16Сбалансированное и несбалансированное деревья
6
8
1
20
10
25
21
30
Слайд 17Основные операции с бинарным деревом поиска
обход дерева;
вставка информации с
новым значением ключа не изменяя свойств дерева поиска;
формирование сбалансированного дерева
поиска;
поиск заданного ключа;
поиск минимального (максимального) ключа;
удаление информации с заданным ключом;
удаление дерева.
Слайд 18Класс для работы с деревом
Type
Ttree=^Tree
Tree=Record
Inf:TInf;
A1,A2:Ttree;
end;
TBtr=Class(tobject)
proot,p,q,v,w:Ttree;
Constructor Create;
Procedure Wrt1;
Procedure Add(Inf:TInf);
Function poisk(k:Tkey):TInf;
Procedure Make(a:Tms;n:word);
. . . . . . . . . . . .
Destructor Free;
end;
Слайд 19Работа с деревом
Var tr:TBtr;
Begin
. . . .
tr:=TBtr.Create;
tr.Add(inf);
tr.Wrt1;
. . .
.
tr.Free;
Слайд 20Создать дерево
Constructor TBtr.create;
Begin
Inherited create;
proot:=nil;
End;
Слайд 21Удалить дерево
Destructor TBtr.Free;
Procedure Del(var p:Ttree);
begin
If (pNil)
then begin
Del(p^.A1);
Del(p^.A2);
Dispose(p);
p:=Nil;
end;
end;
Begin
Del(proot); inherited free;
end;
Слайд 22Симметричный обход слева направо
Procedure TBtr.Wrt1;
Procedure Wr(p:Ttree);
begin
if
pnil then
begin
Wr(p^.A1);
Print(p^.Inf);
Wr(p^.A2);
end;
end;
begin
p:=proot; wr(p)
end;
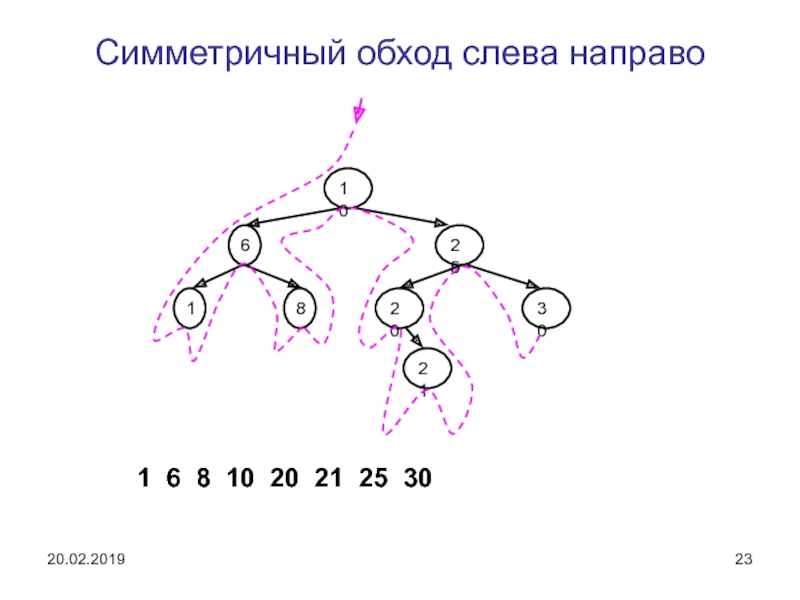
Слайд 23Симметричный обход слева направо
10
25
6
21
30
20
8
1
1 6 8 10 20 21 25
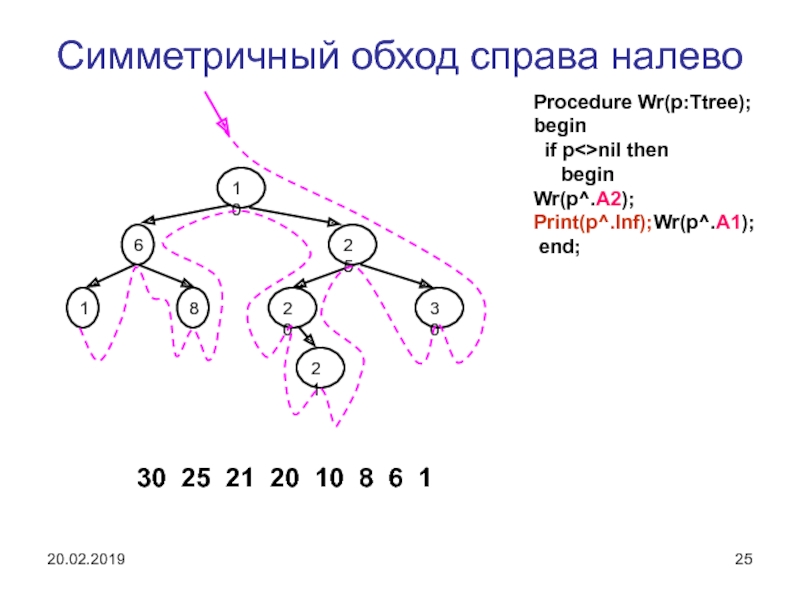
Слайд 24Симметричный обход справа налево
Procedure TBtr.Wrt2;
Procedure Wr(p:Ttree);
begin
if
pnil then
begin
Wr(p^.A2);
Print(p^.Inf);
Wr(p^.A1);
end;
end;
begin
p:=proot; wr(p)
end;
Слайд 25Симметричный обход справа налево
10
25
6
21
30
20
8
1
30 25 21 20 10 8 6
1
Procedure Wr(p:Ttree); begin
if pnil then
begin Wr(p^.A2); Print(p^.Inf); Wr(p^.A1);
end;
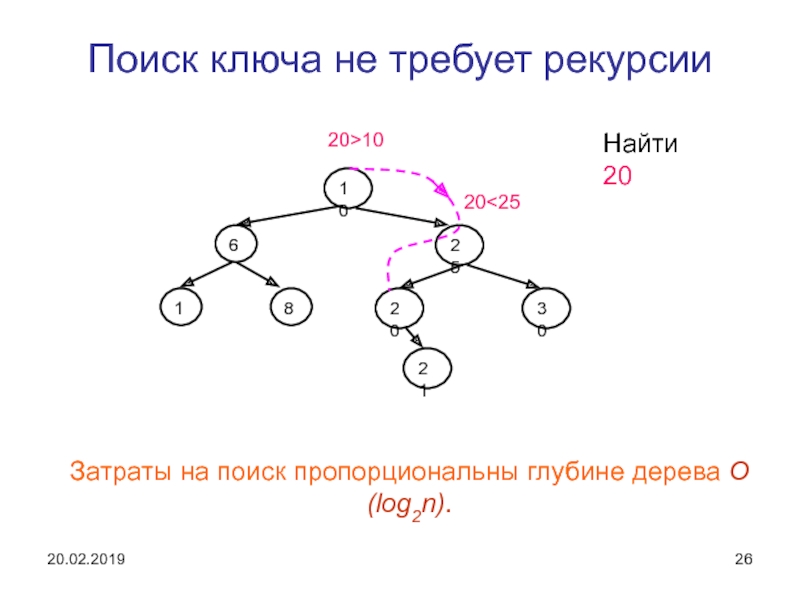
Слайд 26Поиск ключа не требует рекурсии
10
25
6
21
30
20
8
1
Найти 20
20>10
20
дерева О(log2n).
Слайд 27Метод poisk(k)
Const nok:Tkey=’некоторое значениеkey’;
Function TBtr.poisk(k:Tkey):Tinf;
begin p:=Proot;
While(pnil) and (p^.Inf.keyk) do
If k
Result:=p^.inf
else Result.key:=nok;
end;
Обращение к методу
Inf:=tr.poisk(k);
If inf.key=nok then print(’нет ключа’)
else . . .
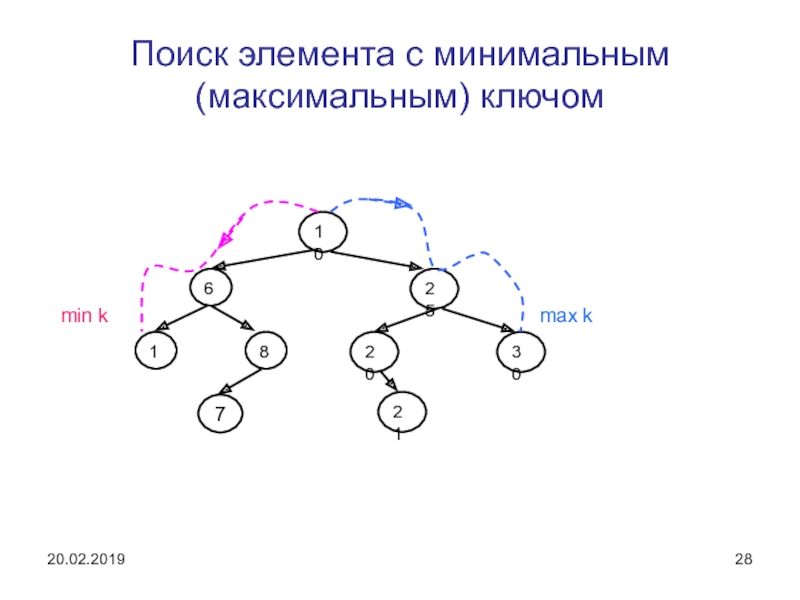
Слайд 28Поиск элемента с минимальным (максимальным) ключом
10
25
6
21
30
20
8
1
7
min k
max k
Слайд 29Методы поиска элемента с минимальным (максимальным) ключом
Function TBtr.Mink:TInf;
begin p:=proot;
While p^.A1Nil do p:=p^.A1;
Result:=p^.Inf;
end;
Function TBtr.Maxk:TInf;
begin p:=proot;
While p^.A2<>Nil do p:=p^.A2;
Result:=p^.Inf;
end;
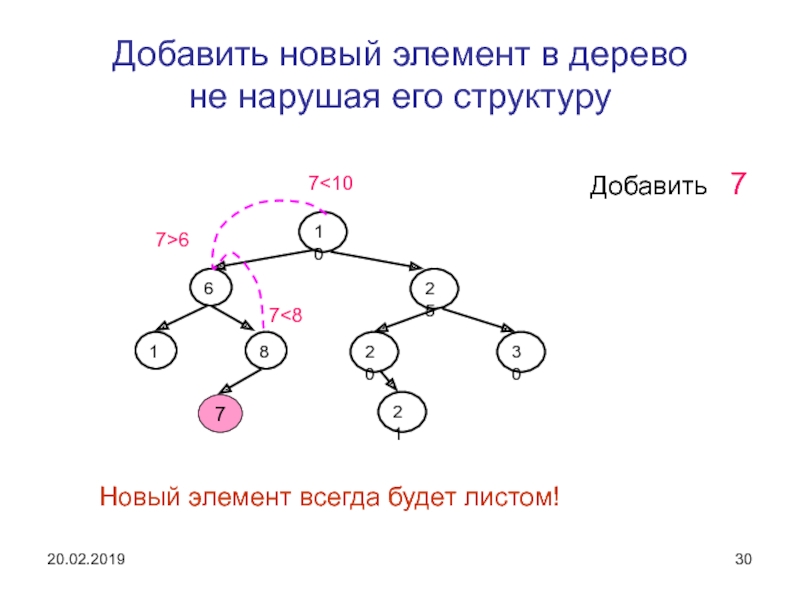
Слайд 30Добавить новый элемент в дерево
не нарушая его структуру
10
25
6
21
30
20
8
1
Добавить
7
76
7
Слайд 31Метод Add(inf) (начало)
Procedure TBtr.Add(Inf:TInf);
Var bl:Boolean;
begin
New(w); // создание нового листа:
w^.Inf:=Inf;
w^.A1:=Nil;
w^.A2:=Nil;
if proot=Nil then proot:=w
else
begin
// добавление листа…
Слайд 32Метод Add(inf) (конец)
// Поиск места для добавления
листа…
p:=proot;
repeat
q:=p; // q -
указатель на предыдущий элемент
bl:=Inf.key
if bl then p:=p^.A1
else p:=p^.A2;
until p=Nil; // добавление листа
if bl then q^.A1:=w
else q^.A2:=w;
end;
end;
Слайд 33Пересылка элементов из произвольного массива в дерева
Пусть имеется некоторый массив
из n значений данных с разными ключами
type Tms=array[1..nr] of
Tinf;
Procedure TBtr.Make(a:Tms;n:word);
begin
For i:=1 to n do Add(a[i]);
end;
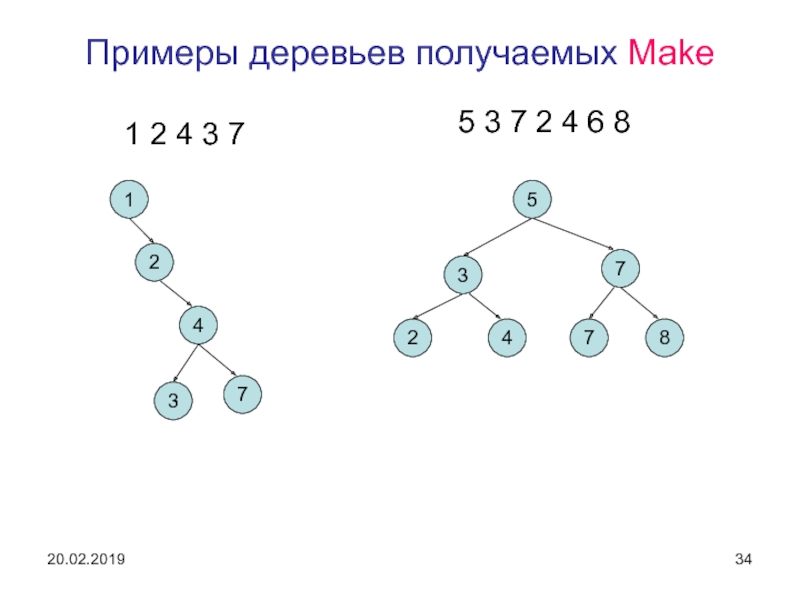
При случайном чередовании ключей в массиве а метод Make обычно формирует дерево неплохо сбалансированное.
Однако, если массив а частично упорядочен, то получается плохо сбалансированное дерево
Слайд 34Примеры деревьев получаемых Make
1 2 4 3 7
1
2
4
3
7
5 3 7
2 4 6 8
5
7
4
3
8
2
7
Слайд 35Распечатать массив в порядке возрастания (убывания) ключа
tr.Make(a:Tms;n:word);
tr.Wrt1;
tr.Wrt2;
Если в методе Wrt1
вместо печати записывать очередной элемент в массив то получаем метод
сортировки. Массив желательно организовать динамический.
Слайд 36Построение сбалансированного дерева поиска (вариант 1)
Procedure TBtr.BLns1(a:Tms;n:word);
Procedure BL(i,j:Word);
Var
m:Word;
begin
if i
begin BL(1,n);
end;
Слайд 37Построение сбалансированного дерева поиска (вариант 2)
Procedure TBtr.BLns2(a:Tms;n:word);
Function BL(i,j:Word):Ttree;
Var
p:Ttree; m:Word;
begin
if i>j then p:=Nil
else begin
m:=i+j div 2;
New(p); p^.inf:=a[m];
p^.A1:=BL(i,m-1);
p^.A2:=BL(m+1,j);
end;
result:=p;
end;
begin proot:=BL(1,n);
end;
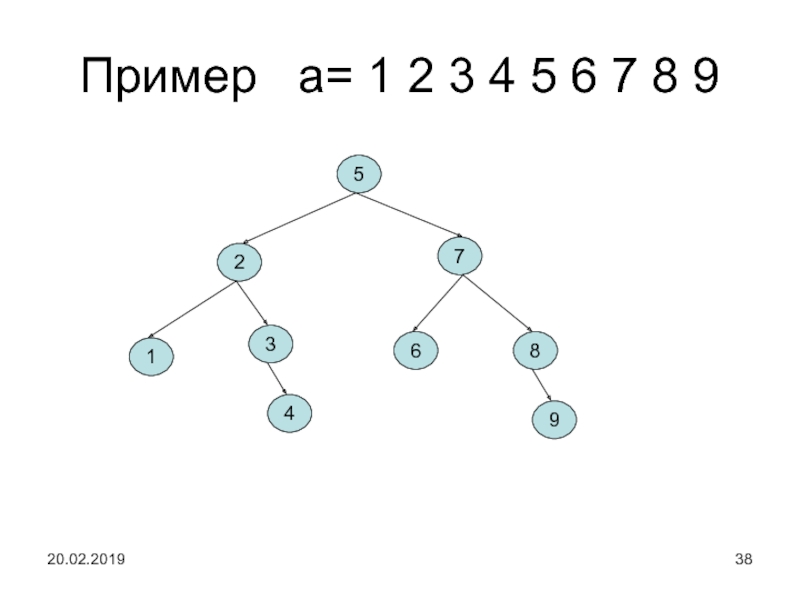
Слайд 38Пример а= 1 2 3 4 5 6 7
8 9
5
2
7
1
3
4
6
8
9
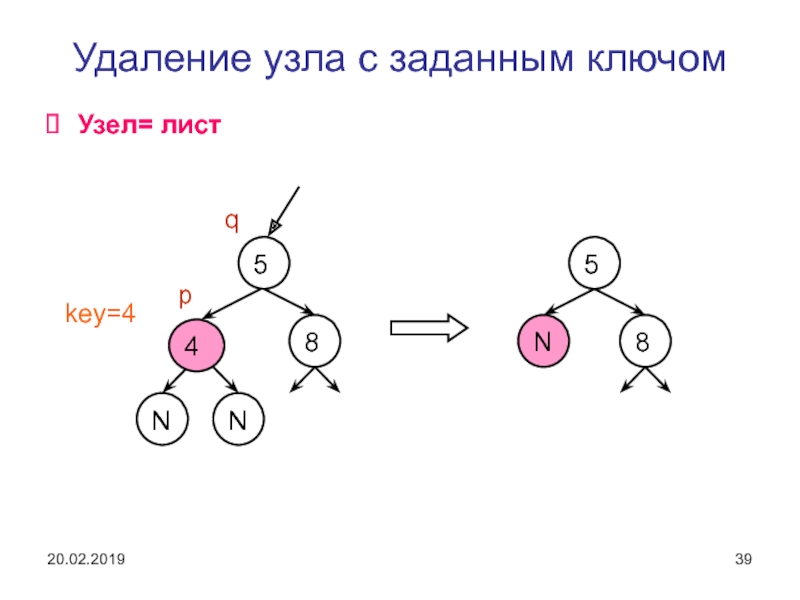
Слайд 39Удаление узла с заданным ключом
Узел= лист
5
8
N
key=4
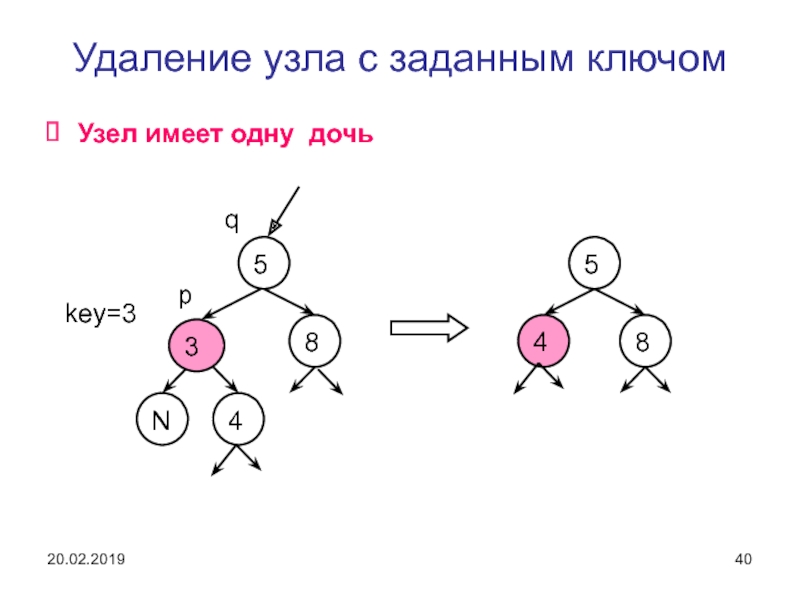
Слайд 40Удаление узла с заданным ключом
Узел имеет одну дочь
5
8
4
key=3
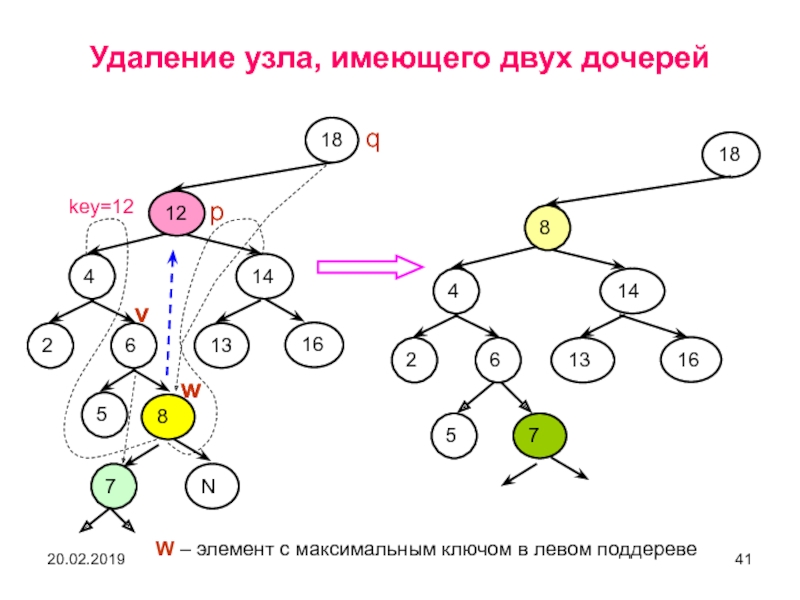
Слайд 41Удаление узла, имеющего двух дочерей
4
2
6
13
16
p
w
8
5
12
key=12
v
14
4
2
6
13
16
18
8
14
W – элемент с максимальным
ключом в левом поддереве
N
7
7
5
Слайд 42Удаление узла, имеющего двух дочерей значительно сложнее.
Если p –
исключаемый узел, то его следует заменить узлом w, который содержит
наибольший ключ в левом поддереве p (либо наименьший ключ в правом поддереве).
Такой узел w является либо листом, либо самым правым узлом поддерева p у которого имеется только левая дочь
Слайд 43Метод удаления Delk(k)
поиск ключа
Procedure Tree.Delk(k:Tkey);
begin
p:=proot;
While (pNil) and (p^.Inf.keyk) do
begin
q:=p;
if p^.Inf.key>k then p:=p^.A1
else p:=p^.A2;
end;
if pNil then
//исключение найденного узла p:
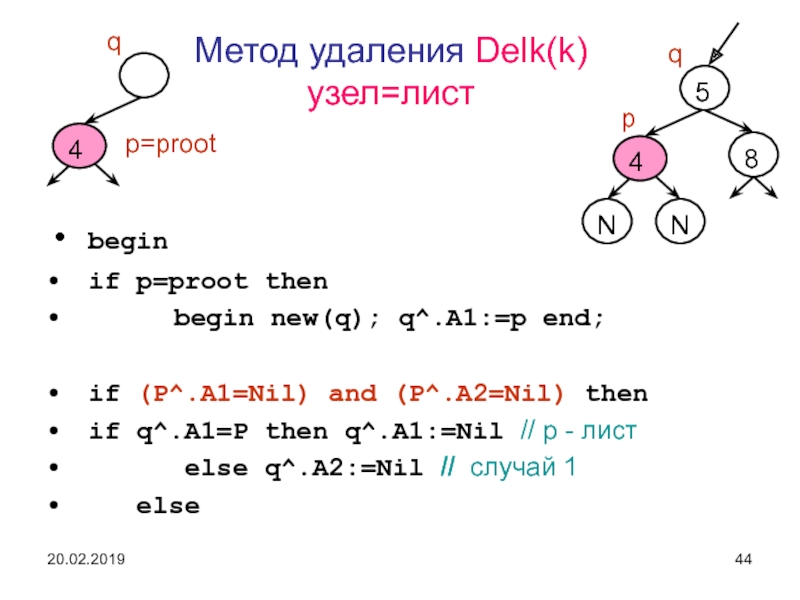
Слайд 44Метод удаления Delk(k)
узел=лист
begin
if p=proot then
begin new(q);
q^.A1:=p end;
if (P^.A1=Nil) and (P^.A2=Nil) then
if q^.A1=P then q^.A1:=Nil //
p - лист
else q^.A2:=Nil // случай 1
else
q
4
p=proot
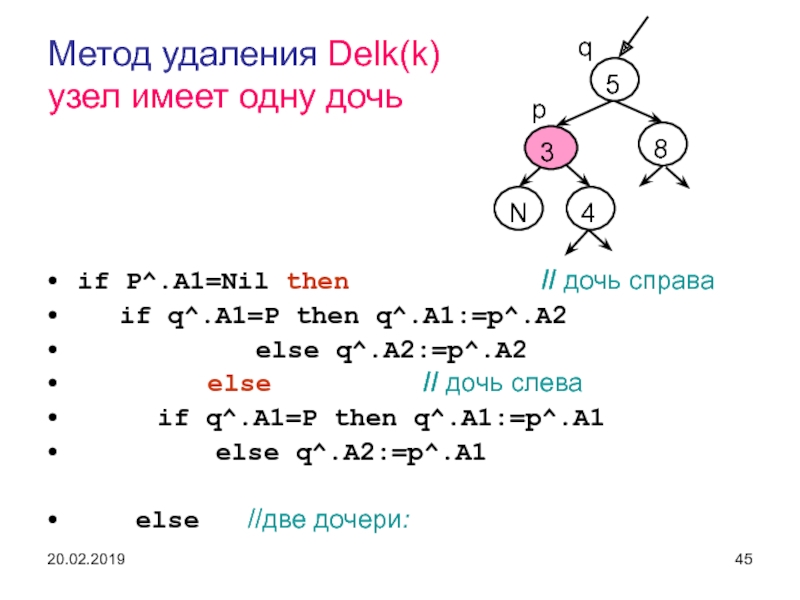
Слайд 45Метод удаления Delk(k)
узел имеет одну дочь
if P^.A1=Nil then
// дочь справа
if q^.A1=P then q^.A1:=p^.A2
else q^.A2:=p^.A2
else // дочь слева
if q^.A1=P then q^.A1:=p^.A1
else q^.A2:=p^.A1
else //две дочери:
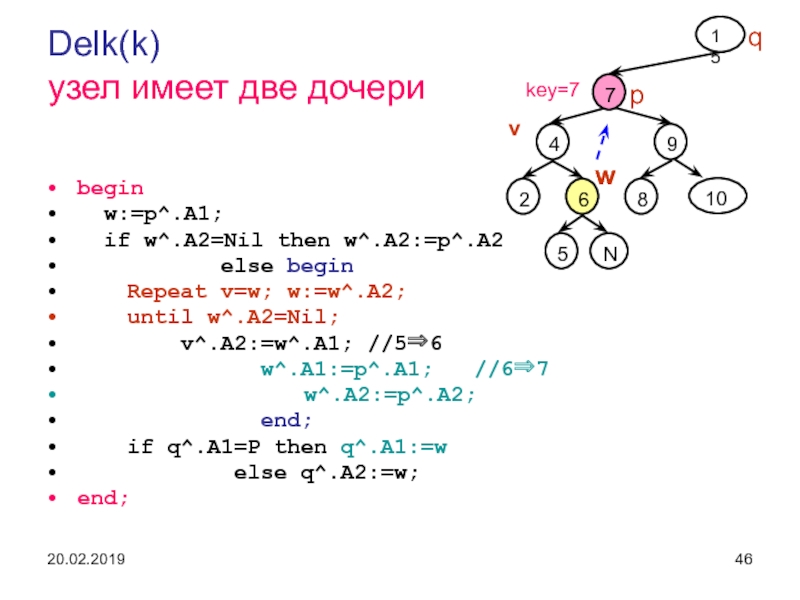
Слайд 46Delk(k)
узел имеет две дочери
begin
w:=p^.A1;
if w^.A2=Nil then
w^.A2:=p^.A2
else begin
Repeat v=w; w:=w^.A2;
until w^.A2=Nil;
v^.A2:=w^.A1;
//56
w^.A1:=p^.A1; //67
w^.A2:=p^.A2;
end;
if q^.A1=P then q^.A1:=w
else q^.A2:=w;
end;
4
2
6
8
10
p
w
N
5
7
15
q
key=7
9
v
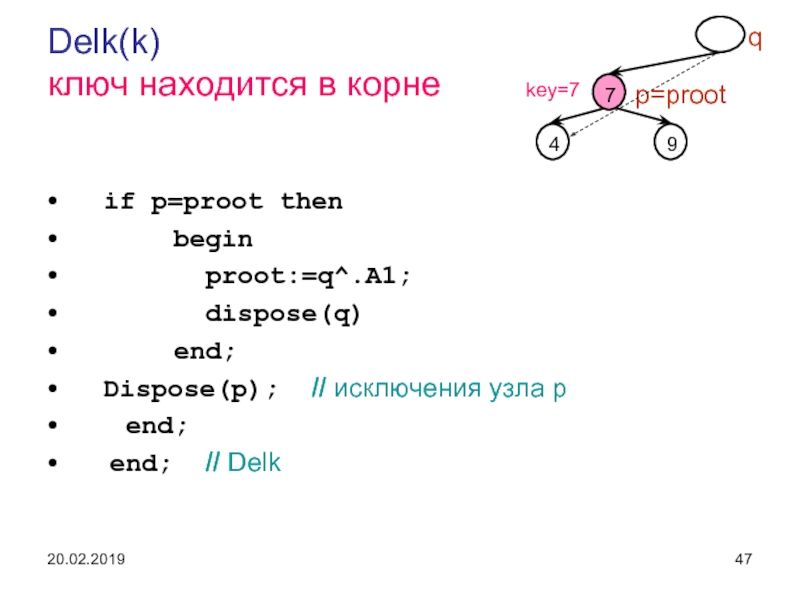
Слайд 47Delk(k)
ключ находится в корне
if p=proot then
begin
proot:=q^.A1;
dispose(q)
end;
Dispose(p); // исключения узла p
end;
end; // Delk
4
p=proot
7
q
key=7
9
Слайд 48Контрольные вопросы
Дайте определение основным понятиям древовидной структуры – корень, узел,
лист, порядок узла, порядок дерева, глубина листа, глубина дерева, определение
сбалансированного дерева.
Напишите рекурсивный тип, используемый для работы с деревом данных и поясните как формируется дерево.
Напишите процедуры обхода дерева в прямом и обратном порядке и проиллюстрируйте результат обхода дерева на рис.7.1.
Дайте определение бинарного дерева поиска и опишите его особенности.
По заданному отсортированному массиву нарисуйте сбалансированное дерево поиска.
Напишите методы симметричного обхода бинарного дерева, поиска элемента с заданным ключом, вставки нового элемента, удаления элемента с заданным ключом.
Слайд 49Задачи на экзамен
№13
Ввести массив записей со случайным распределением ключей {a[i]:TInf}
(Inf.F - фамилия; Inf.к - учетный номер) из StringGrid1 в
двоичное дерево поиска методом Add
после чего прочитать его в StringGrid2 методом Wrt1.
Методы класса Add и Wrt1 оформить в отдельном модуле.
Слайд 50Задачи на экзамен
№14
Ввести массив записей со случайным распределением ключей {a[i].Inf}
(Inf.F - фамилия; Inf.к - учетный номер) из StringGrid1 в
двоичное дерево поиска процедурой Add,
после чего найти в дереве поиска и распечатать в Memo1 запись с ключом k, введенным из Edit1.
Методы класса Add и Poisk оформить в отдельном модуле.
Слайд 51Задачи на экзамен
№15
Ввести массив записей с упорядоченным распределением ключей {a[i]:TInf
} (Inf.F - фамилия; Inf.к - учетный номер) из StringGrid1
в двоичное идеально сбалансированное дерево с помощью метода Blns.
После чего найти в дереве поиска с помощью функии Mink и распечатать в Memo1 запись с минимальным ключом.
Методы класса Blns , Mink оформить в отдельном модуле.





























![Тема 7 Древовидные структуры данных Задачи на экзамен№13Ввести массив записей со случайным распределением ключей {a[i]:TInf} (Inf.F Задачи на экзамен№13Ввести массив записей со случайным распределением ключей {a[i]:TInf} (Inf.F - фамилия; Inf.к - учетный номер)](/img/thumbs/6336b3a402ac99ed7e714db47cd7e9d4-800x.jpg)
![Тема 7 Древовидные структуры данных Задачи на экзамен№14Ввести массив записей со случайным распределением ключей {a[i].Inf} (Inf.F Задачи на экзамен№14Ввести массив записей со случайным распределением ключей {a[i].Inf} (Inf.F - фамилия; Inf.к - учетный номер)](/img/tmb/4/303501/1f0043370965822b09833bda725a801a-800x.jpg)
![Тема 7 Древовидные структуры данных Задачи на экзамен№15Ввести массив записей с упорядоченным распределением ключей {a[i]:TInf } Задачи на экзамен№15Ввести массив записей с упорядоченным распределением ключей {a[i]:TInf } (Inf.F - фамилия; Inf.к - учетный](/img/thumbs/b6e2209850bce966a942ccb2a207ba0c-800x.jpg)



















