Тема 8. ДИФРАКЦИЯ СВЕТА 8.1. Принцип Гюйгенса-Френеля Сегодня: вторник, 19

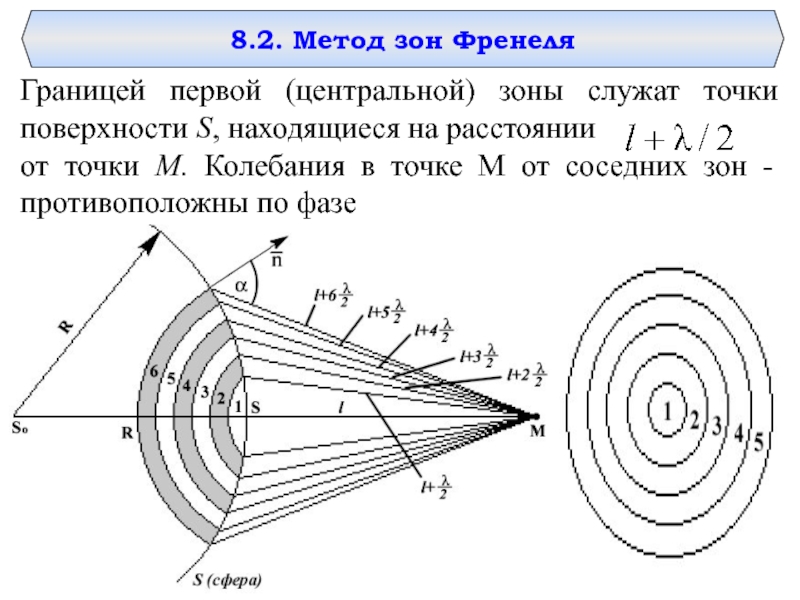
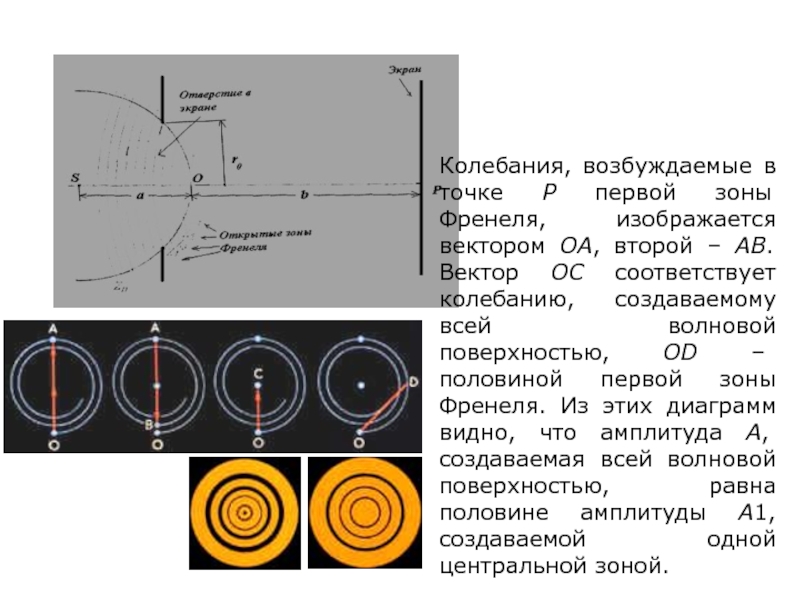
зон Френеля
8.3. Дифракция Френеля от простейших
преград
8.4. Дифракция в параллельных

лучах
(дифракция Фраунгофера)

8.5. Дифракция на пространственных решетках.
Дифракция рентгеновских лучей

8.6. Понятие о голографии

интенсивности I;

б – дифракционная картина

при распространении света в среде с резкими неоднородностями, размеры которых

сравнимы с длинной волны, и связанных с отклонениями от законов геометрической оптики.

точка, до которой доходит волна, служит центром вторичных волн, а

огибающая этих волн задает положение волнового фронта в следующий момент времени.

источник вторичных волн.
Френель существенно развил этот принцип.
• Все

вторичные источники фронта волны, исходящей из одного источника, когерентны между собой.
• Равные по площади участки волновой поверхности излучают равные интенсивности.
Каждый вторичный источник излучает свет преимущественно в направлении внешней нормали к волновой поверхности в этой точке.
Для вторичных источников справедлив принцип суперпозиции.

S, находящиеся на расстоянии
от точки M. Колебания в точке

M от соседних зон - противоположны по фазе

друга:
площади соседних зон одинаковы, а амплитуды
при
,
, число
зон
, а

радиус первой зоны

.

Амплитуды волн, приходящих в точку M от соседних зон примерно равны.

точке M всей сферической поверхностью, равна половине амплитуды, создаваемой одной

лишь центральной зоной, а интенсивность

.

Интенсивность света увеличивается, если закрыть все четные зоны:

поверхности

0,5bm/(a + b).
Если расстояние a до источника света S и

расстояние b до точки наблюдения P много больше размеров зон Френеля, то радиус rm

Найдём радиус m-ой зоны Френеля. Как следует из геометрических соображений

Вид дифракционной картины зависит от числа зон Френеля,

открываемых отверстием.

a

b

(а) и четном (б) числе зон

по ширине кольцевые зоны. Колебание, создаваемое в точке наблюдения P

каждой из зон, изображается вектором A, длина которого равна амплитуде колебаний, а угол  дает начальную фазу. При сложении таких векторов получается векторная диаграмма (a). В пределе, при стремлении ширины зон к нулю, векторная диаграмма принимает вид спирали (б).

OA, второй – AB. Вектор OC соответствует колебанию, создаваемому всей

волновой поверхностью, OD – половиной первой зоны Френеля. Из этих диаграмм видно, что амплитуда A, создаваемая всей волновой поверхностью, равна половине амплитуды A1, создаваемой одной центральной зоной.

в области геометрической тени от круглого диска: светлое пятнышко (так

называемое пятно Пуассона) создается вторичными волнами первой кольцевой зоны Френеля, окружающей экран.

8.5. Дифракция от диска

Дифракционная картина от круглого диска; в центре геометрической тени – светлое пятно – пятно Пуассона

такой же, как и в отсутствие экрана. Вследствие симметрии центральная

светлая точка будет окружена кольцами света и тени «Пятно Пуассона» (вне границ геометрической тени).