Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема: Интеграл и его практическое применение Выполнил : Петрова
Содержание
- 1. Тема: Интеграл и его практическое применение Выполнил : Петрова
- 2. Немного истории -1675 г, опубликовано в 1686
- 3. Евдокс Книдский408 – 355 до н. эАрхимед287
- 4. «Интеграл» придумал Я.Бернулли (1690)«восстанавливать» от латинского integro«целый» от латинского integer
- 5. Лейбниц Готфрид Вильгельм (1646-1716) « Общее
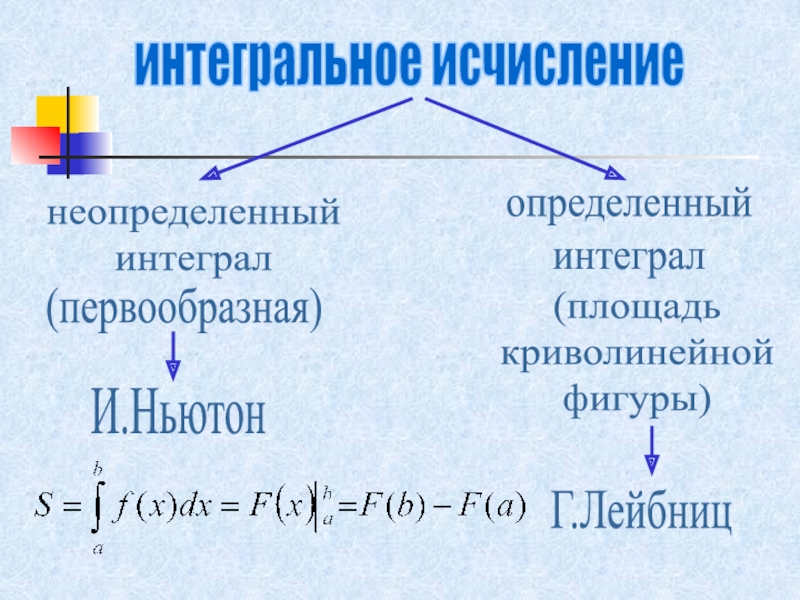
- 6. интегральное исчислениенеопределенный интегралопределенныйинтеграл(первообразная)(площадь криволинейной фигуры)И.НьютонГ.Лейбниц
- 7. Слайд 7
- 8. Уже Архимед успешно находил площади фигур, несмотря
- 9. ЗаключениеПрименение физических моделей при введении понятия интеграла,
- 10. Скачать презентанцию
Немного истории -1675 г, опубликовано в 1686 гввел Г.Лейбниц- 1675 г, Ж Лагранж5 век до н.э. др.гр. ученый Демокрит3-4 век до н.э. Архимед ввел метод исчерпывания
Слайды и текст этой презентации
Слайд 1Тема: «Интеграл и его практическое применение»
Выполнил:
Петрова Анастасия ,
Студент группы
1ИС.
Слайд 2Немного истории
-1675 г, опубликовано в 1686 г
ввел Г.Лейбниц
- 1675 г,
Ж Лагранж
5 век до н.э. др.гр. ученый Демокрит
3-4 век до
н.э. Архимед ввел метод исчерпыванияСлайд 3Евдокс Книдский
408 – 355 до н. э
Архимед
287 – 212 до
н.э.
Строгое изложение теории интегралов появилось только в 19 веке. Но
задачами на вычисление площадей занимались математики Древней Греции.Математики Древней Греции
Слайд 4
«Интеграл» придумал Я.Бернулли (1690)
«восстанавливать» от латинского integro
«целый» от латинского integer
Слайд 5Лейбниц Готфрид Вильгельм
(1646-1716)
« Общее искусство знаков представляет чудесное
пособие, так как оно разгружает воображение… Следует заботиться о том,
чтобы обозначения были удобны для открытий. Обозначения коротко выражают и отображают сущность вещей. Тогда поразительным образом сокращается работа мысли.»Лейбниц
Слайд 6интегральное исчисление
неопределенный
интеграл
определенный
интеграл
(первообразная)
(площадь
криволинейной
фигуры)
И.Ньютон
Г.Лейбниц
Слайд 8Уже Архимед успешно находил площади фигур, несмотря на то, что
в математике его времени не было понятия интеграла
Но лишь интегральное
исчисление дает общий метод решения задач из различных областей наук.Недаром даже поэты воспевали интеграл.
Смысл- там, где змеи интеграла
Меж цифр и букв , меж d и f.
Там – власть, там творческие горны!
Пред волей чисел все – рабы.
И солнца путь вершат, покорны
Немым речам и ворожбы.
В.Брюсов.