Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема: Интеграл. Определенный интеграл. Свойства. Примеры. Применение
Содержание
- 1. Тема: Интеграл. Определенный интеграл. Свойства. Примеры. Применение
- 2. Определение интегралаИнтеграл - одно из важнейших понятий математического
- 3. Понятие определенного интеграла Пусть функция y = f(x) определена на отрезке [a, b], a
- 4. С геометрической точки зрения эта сумма σ представляет
- 5. Понятие определенного интеграла Определение. Если существует конечный предел
- 6. Понятие определенного интеграла Теорема 1. Если функция y = f(x) непрерывна на
- 7. Основные свойства определенного интеграла 1. Значение определенного интеграла
- 8. Основные свойства определенного интеграла 4. Если функция y = f(x) интегрируема на [a, b] и a
- 9. Пример решенийПример 1Вычислить определенный интегралРешение:(1) Выносим константу
- 10. Пример решений(3) Используем формулу Ньютона-Лейбница Сначала подставляем в
- 11. Пример решений(1) Используем свойства линейности определенного интеграла.(2)
- 12. Вычисление длин дуг с помощью определённого интегралаЕсли
- 13. Вычисление площадей с помощью определенного интеграла Площадь
- 14. Вычисление объемов с помощью определенного интеграла Если
- 15. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Тема: «Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для
нахождения длин, площадей и объемов».
Слайд 2Определение интеграла
Интеграл - одно из важнейших понятий математического анализа, которое возникает
при решении задач о нахождении площади под кривой, пройденного пути
при неравномерном движении, массы неоднородного тела, и тому подобных, а также в задаче о восстановлении функции по её производной (неопределённый интеграл). Упрощённо интеграл можно представить как аналог суммы для бесконечного числа бесконечно малых слагаемых. В зависимости от пространства, на котором задана подынтегральная функция, интеграл может быть — двойной, тройной, криволинейный, поверхностный и так далее; также существуют разные подходы к определению интеграла — различают интегралы Римана, Лебега, Стилтьеса и другиеСлайд 3 Понятие определенного интеграла
Пусть функция y = f(x) определена на отрезке [a, b], a
разобьем [a, b] точками a = x0
[xi-1, xi ], ..., [xn-1, xn ];2) в каждом из частичных отрезков [xi-1, xi ], i = 1, 2, ... n, выберем произвольную точку и вычислим значение функции в этой точке: f(zi);
3) найдем произведения f(zi) · Δxi, где – длина частичного отрезка [xi-1, xi ], i = 1, 2, ... n;
4) составим интегральную сумму функции y = f(x) на отрезке [a, b]:
Слайд 4С геометрической точки зрения эта сумма σ представляет собой сумму площадей
прямоугольников, основания которых – частичные отрезки [x0, x1], [x1, x2], ..., [xi-1, xi ],
..., [xn-1, xn ], а высоты равны f(z1), f(z2), ..., f(zn) соответственно (рис. 1). Обозначим через λ длину наибольшего частичного отрезка:Понятие определенного интеграла
5) найдем предел интегральной суммы, когда λ → 0.
Слайд 5Понятие определенного интеграла
Определение. Если существует конечный предел интегральной суммы (1) и
он не зависит ни от способа разбиения отрезка [a, b] на частичные
отрезки, ни от выбора точек zi в них, то этот предел называется определенным интегралом от функции y = f(x) на отрезке [a, b] и обозначается Таким образом,В этом случае функция f(x) называется интегрируемой на [a, b]. Числа a и b называются соответственно нижним и верхним пределами интегрирования, f(x) – подынтегральной функцией, f(x)dx – подынтегральным выражением, x – переменной интегрирования; отрезок [a, b] называется промежутком интегрирования.
Слайд 6Понятие определенного интеграла
Теорема 1. Если функция y = f(x) непрерывна на отрезке [a, b], то она
интегрируема на этом отрезке.
Определенный интеграл с одинаковыми пределами интегрирования равен
нулю:Если a > b, то, по определению, полагаем
Слайд 7Основные свойства определенного интеграла
1. Значение определенного интеграла не зависит от обозначения
переменной интегрирования:
2. Постоянный множитель можно выносить за знак определенного интеграла:
3.
Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме определенных интегралов от этих функций:Слайд 8Основные свойства определенного интеграла
4. Если функция y = f(x) интегрируема на [a, b] и a
среднем). Если функция y = f(x) непрерывна на отрезке [a, b], то на этом отрезке
существует точка , такая, чтоСлайд 9Пример решений
Пример 1
Вычислить определенный интеграл
Решение:
(1) Выносим константу за знак интеграла.
(2)
Интегрируем по таблице с помощью самой популярной формулы
Появившуюся константу
целесообразно отделить от и вынести за скобку. Слайд 10Пример решений
(3) Используем формулу Ньютона-Лейбница
Сначала подставляем в верхний предел,
затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный
ответ.Пример 2
Вычислить определенный интеграл
Решение:
Слайд 11Пример решений
(1) Используем свойства линейности определенного интеграла.
(2) Интегрируем по таблице,
при этом все константы выносим – они не будут участвовать
в подстановке верхнего и нижнего предела.(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница:
Слайд 12Вычисление длин дуг с помощью определённого интеграла
Если
- параметрические уравнения гладкой кривой, то длина ее дуги равна , где и - производные функций
и соответственно, по параметру .
Существует аналогичная формула для длины дуги пространственной гладкой кривой:
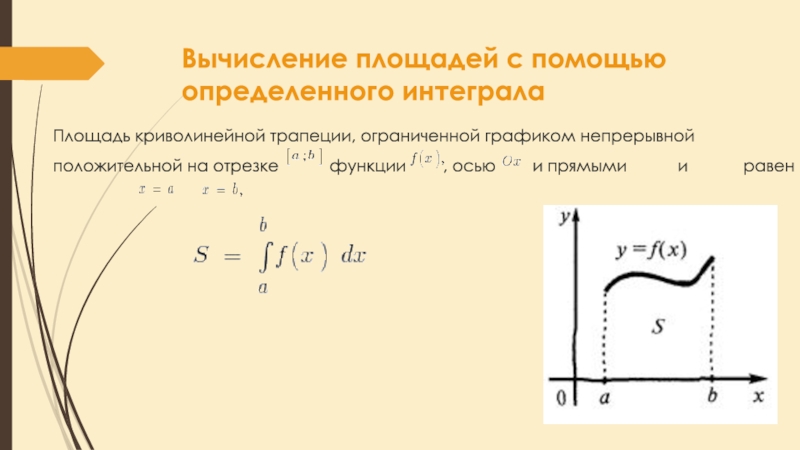
Слайд 13Вычисление площадей с помощью определенного интеграла
Площадь криволинейной трапеции, ограниченной графиком
непрерывной положительной на отрезке функции
, осью и прямыми и равенСлайд 14Вычисление объемов с помощью определенного интеграла
Если тело заключено между двумя
перпендикулярными к оси плоскостями, проходящими через точки
и тоГде — площадь сечения тела плоскостью, которая проходит через точку и перпендикулярна к оси


![Тема: Интеграл. Определенный интеграл. Свойства. Примеры. Применение Понятие определенного интеграла Пусть функция y = f(x) определена на отрезке [a, b], a Понятие определенного интеграла Пусть функция y = f(x) определена на отрезке [a, b], a](/img/tmb/6/589128/32ed495759404887f3202d561e58a103-800x.jpg)
![Тема: Интеграл. Определенный интеграл. Свойства. Примеры. Применение С геометрической точки зрения эта сумма σ представляет собой сумму площадей прямоугольников, С геометрической точки зрения эта сумма σ представляет собой сумму площадей прямоугольников, основания которых – частичные отрезки [x0, x1],](/img/tmb/6/589128/308000c2820dad607d4c305f53bfbd46-800x.jpg)

![Тема: Интеграл. Определенный интеграл. Свойства. Примеры. Применение Понятие определенного интеграла Теорема 1. Если функция y = f(x) непрерывна на отрезке [a, b], то она Понятие определенного интеграла Теорема 1. Если функция y = f(x) непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.Определенный интеграл с](/img/tmb/6/589128/2b46bd62201408750c27d12eb69f0630-800x.jpg)

![Тема: Интеграл. Определенный интеграл. Свойства. Примеры. Применение Основные свойства определенного интеграла 4. Если функция y = f(x) интегрируема на [a, b] и a Основные свойства определенного интеграла 4. Если функция y = f(x) интегрируема на [a, b] и a](/img/tmb/6/589128/be867a8e9145e556e9075796581d2ce8-800x.jpg)