Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема: Параллельное проектирование. Площадь ортогональной проекции. Изображение
Содержание
- 1. Тема: Параллельное проектирование. Площадь ортогональной проекции. Изображение
- 2. Чертеж - хорошее средство для получения и
- 3. Параллельное проектированиеПусть π - некоторая плоскость, l
- 4. Параллельное проектирование для объемных фигур.Если рассматривать любую
- 5. Соотношения пространственных фигур их изображениям на плоскостиФигура в пространствеЕё изображение на плоскостиПроизвольный треугольникПроизвольный треугольник
- 6. Прямоугольный треугольникПроизвольный треугольникРавнобедренный треугольникПроизвольный треугольникФигура в пространствеЕё изображение на плоскости
- 7. Равносторонний треугольникПроизвольный треугольникПараллелограммПроизвольный параллелограммПрямоугольникПроизвольный параллелограммЕё изображение на плоскостиФигура в пространстве
- 8. Фигура в пространствеЕё изображение на плоскостиКвадратПроизвольный параллелограммТрапецияПроизвольная трапецияПроизвольный параллелограммРомб
- 9. Фигура в пространствеЕё изображение на плоскостиРавнобокая трапецияПроизвольная трапецияПрямоугольная трапецияПроизвольная трапецияКруг (окружность)Овал (эллипс)
- 10. Свойство №1Если прямая параллельна или совпадает с
- 11. Свойство №2Параллельное проектирование сохраняет отношение длин отрезков,
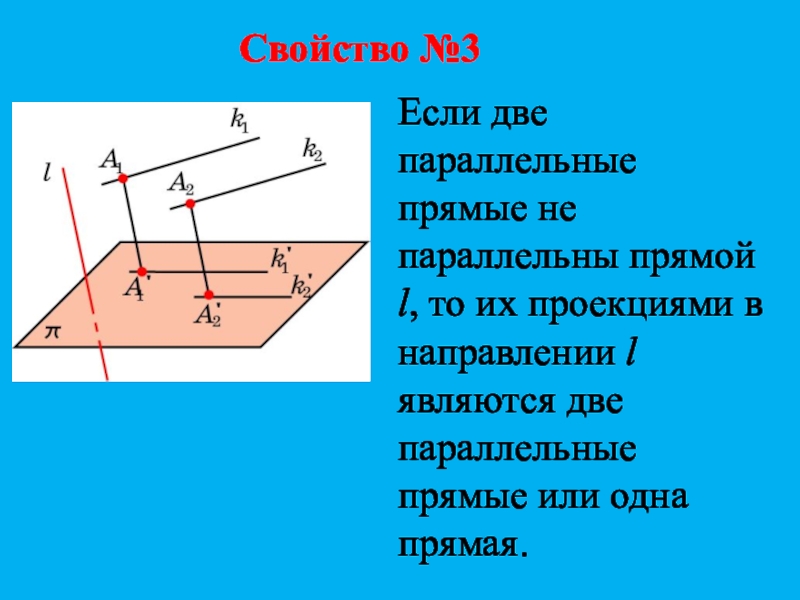
- 12. Свойство №3Если две параллельные прямые не параллельны
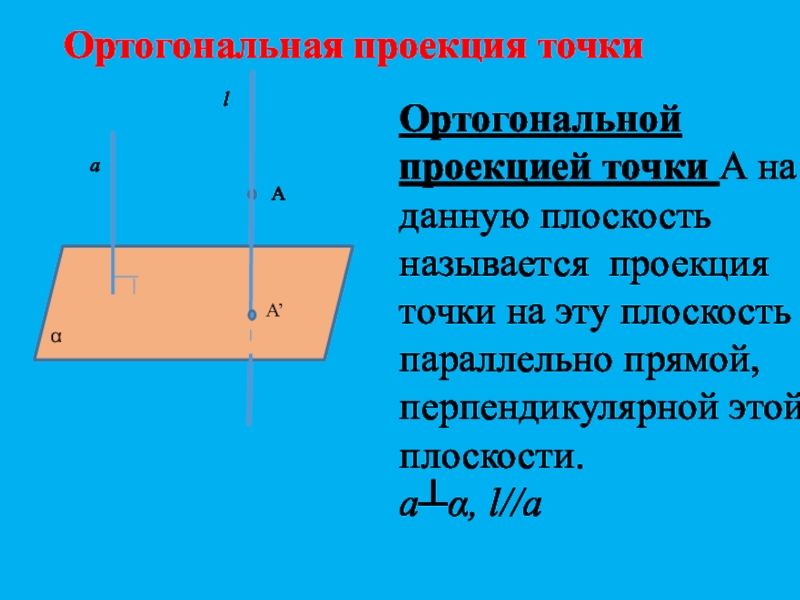
- 13. Ортогональная проекция точкиОртогональной проекцией точки А на
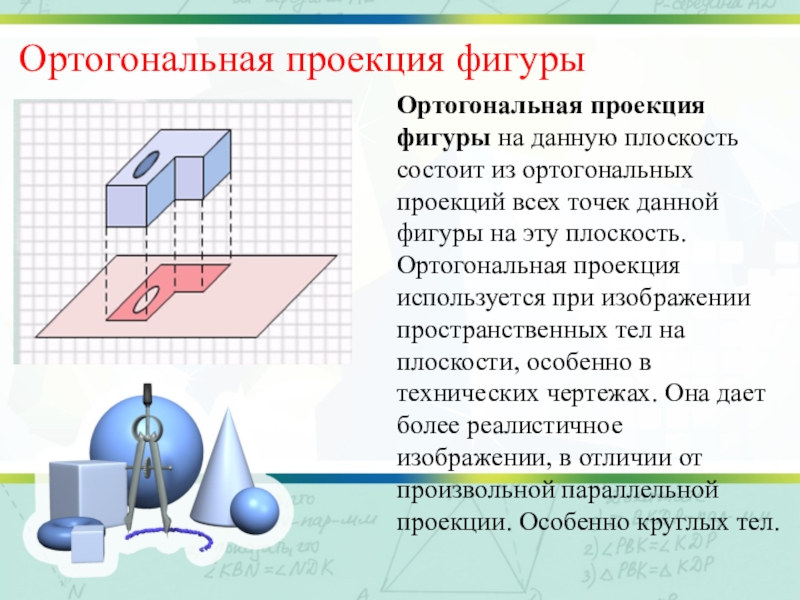
- 14. Ортогональная проекция фигурыОртогональная проекция фигуры на данную
- 15. Алгоритм изображения пирамиды.1. Изображение пирамиды начинают всегда
- 16. Построить изображение пирамиды в основании которой лежит
- 17. Задача №2Построить изображение пирамиды в основании которой
- 18. Задача №3Построить изображение пирамиды в основании которой
- 19. Задача №4Построить изображение пирамиды в основании которой
- 20. Задача №5Построить изображение пирамиды в основании которой
- 21. Задача №6Построить изображение пирамиды в основании которой
- 22. Алгоритм изображения призмы.1. Изображение призмы начинают всегда
- 23. Построить изображение призмы в основании которой лежит
- 24. Задача №2Построить изображение призмы в основании которой
- 25. Задача №3Построить изображение призмы в основании которой
- 26. Задача №4Построить изображение призмы в основании которой
- 27. Задача №5Построить изображение пирамиды в основании которой
- 28. Задача №6Построить изображение пирамиды в основании которой
- 29. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Тема: Параллельное проектирование. Площадь ортогональной проекции.
Изображение пространственных фигур.
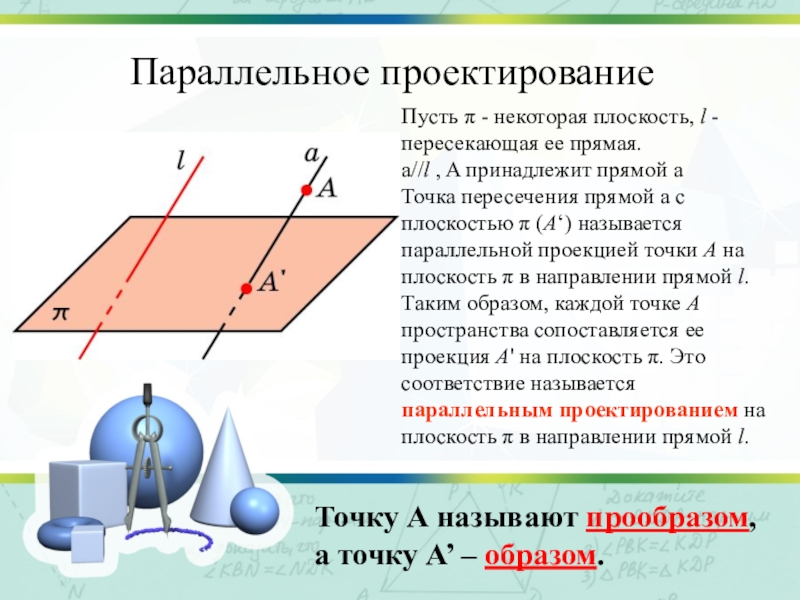
Слайд 3Параллельное проектирование
Пусть π - некоторая плоскость, l - пересекающая ее
прямая.
a//l , A принадлежит прямой a
Точка пересечения прямой a
с плоскостью π (A‘) называется параллельной проекцией точки A на плоскость π в направлении прямой l.Таким образом, каждой точке A пространства сопоставляется ее проекция A' на плоскость π. Это соответствие называется параллельным проектированием на плоскость π в направлении прямой l.
Точку А называют прообразом, а точку А’ – образом.
Слайд 4Параллельное проектирование для объемных фигур.
Если рассматривать любую геометрическую фигуру как
множество точек, можно построить в заданной плоскости проекцию данной фигуры.
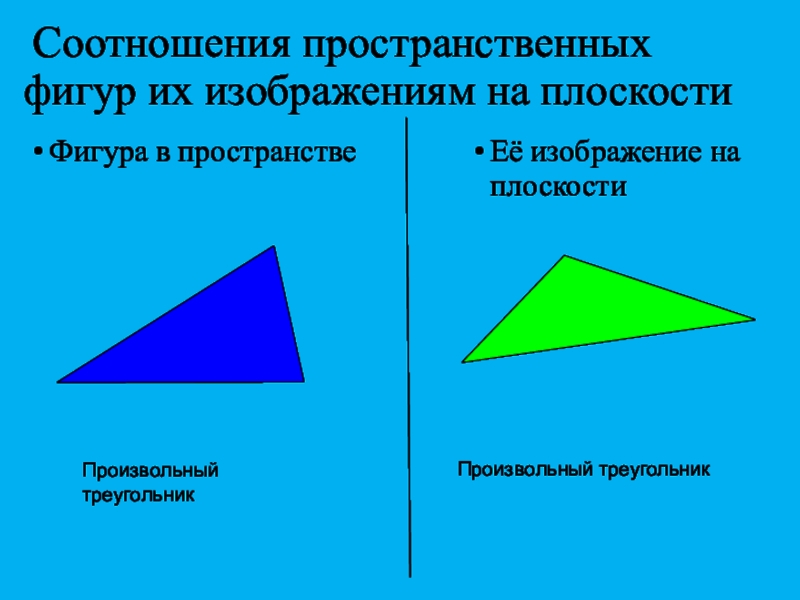
Таким образом можно получить изображение (или «проекцию») любой пространственной фигуры на плоскость.Слайд 5 Соотношения пространственных фигур их изображениям на плоскости
Фигура в пространстве
Её
изображение на плоскости
Произвольный треугольник
Произвольный треугольник
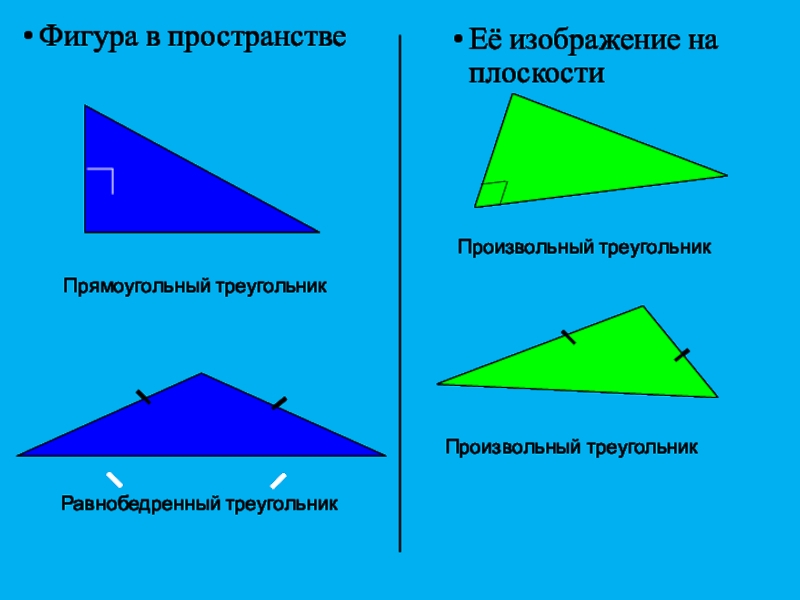
Слайд 6Прямоугольный треугольник
Произвольный треугольник
Равнобедренный треугольник
Произвольный треугольник
Фигура в пространстве
Её изображение на плоскости
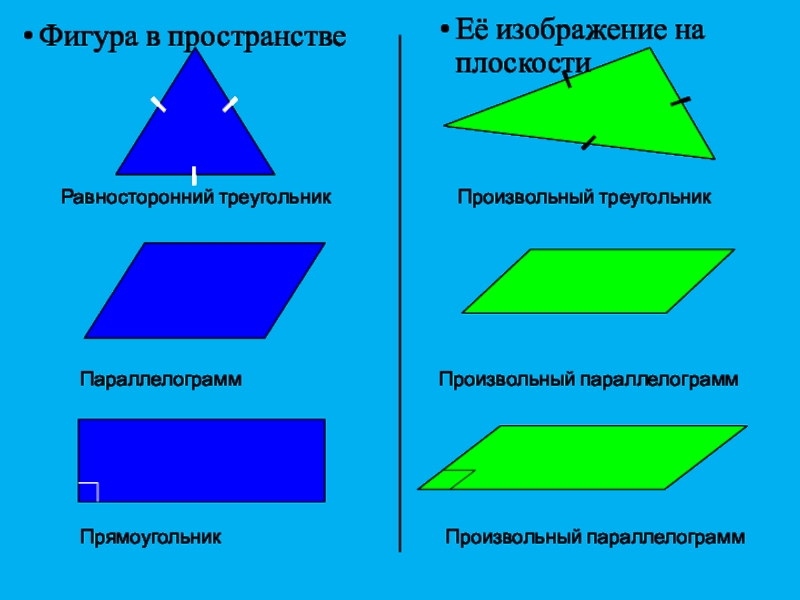
Слайд 7Равносторонний треугольник
Произвольный треугольник
Параллелограмм
Произвольный параллелограмм
Прямоугольник
Произвольный параллелограмм
Её изображение на плоскости
Фигура в пространстве
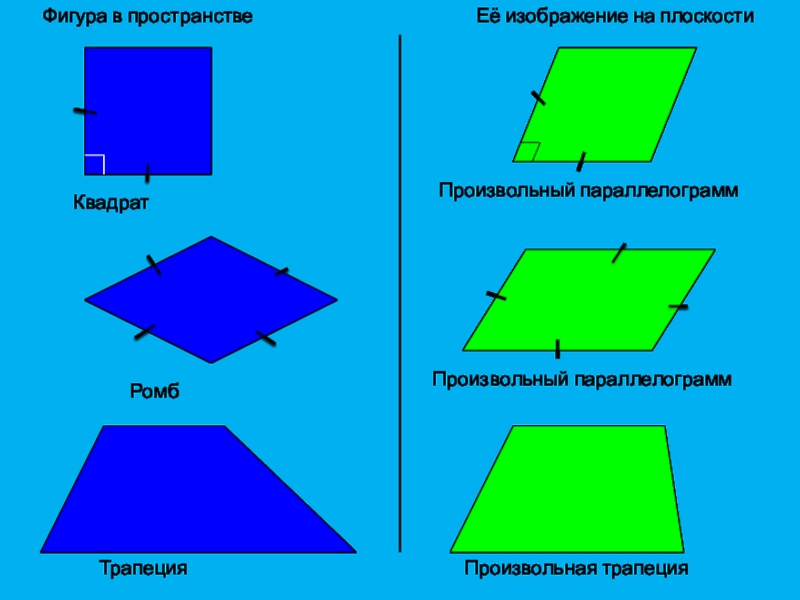
Слайд 8Фигура в пространстве
Её изображение на плоскости
Квадрат
Произвольный параллелограмм
Трапеция
Произвольная трапеция
Произвольный параллелограмм
Ромб
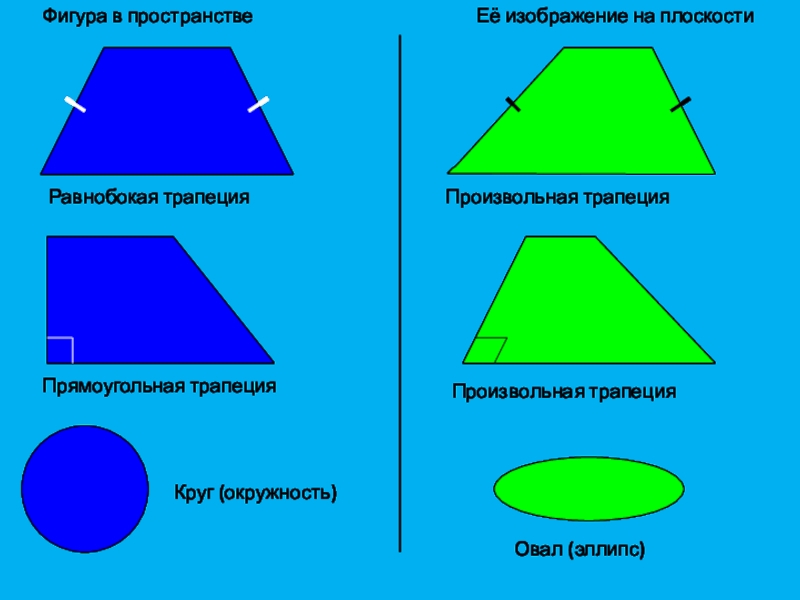
Слайд 9Фигура в пространстве
Её изображение на плоскости
Равнобокая трапеция
Произвольная трапеция
Прямоугольная трапеция
Произвольная трапеция
Круг
(окружность)
Овал (эллипс)
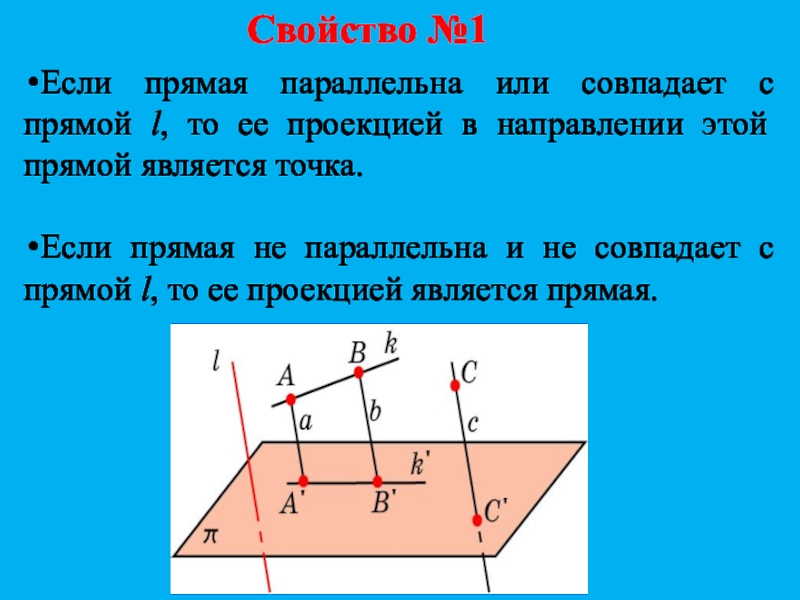
Слайд 10Свойство №1
Если прямая параллельна или совпадает с прямой l, то
ее проекцией в направлении этой прямой является точка.
Если прямая
не параллельна и не совпадает с прямой l, то ее проекцией является прямая.Слайд 11Свойство №2
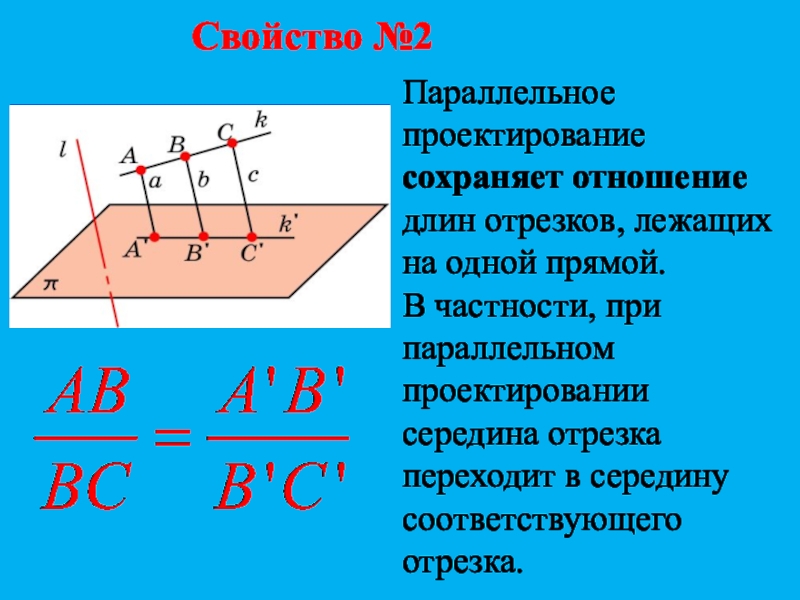
Параллельное проектирование сохраняет отношение длин отрезков, лежащих на одной
прямой.
В частности, при параллельном проектировании середина отрезка переходит в
середину соответствующего отрезка.Слайд 12Свойство №3
Если две параллельные прямые не параллельны прямой l, то
их проекциями в направлении l являются две параллельные прямые или
одна прямая.Слайд 13Ортогональная проекция точки
Ортогональной проекцией точки А на данную плоскость называется
проекция точки на эту плоскость параллельно прямой, перпендикулярной этой плоскости.
a┴α,
l//aСлайд 14Ортогональная проекция фигуры
Ортогональная проекция фигуры на данную плоскость состоит из
ортогональных проекций всех точек данной фигуры на эту плоскость. Ортогональная
проекция используется при изображении пространственных тел на плоскости, особенно в технических чертежах. Она дает более реалистичное изображении, в отличии от произвольной параллельной проекции. Особенно круглых тел.Слайд 15Алгоритм изображения пирамиды.
1. Изображение пирамиды начинают всегда с изображения ее
основания:
Вершины основания пирамиды выбираем так, чтобы получить наиболее наглядное изображение;
Далее
вершины соединяются тонкой вспомогательной линией;2. Построение высоты пирамиды:
Исходя из свойств пирамиды и свойств многоугольника, лежащего в основании строится основание высоты;
Высота изображается вертикальным отрезком, параллельным краю листа бумаги.
3. Построение боковых ребер:
Вершина пирамиды соединяется отрезками с вершинами основания.
4. Невидимые отрезки отмечаем штриховой линией.
5. Выделяем контур.
Слайд 16Построить изображение пирамиды в основании которой лежит равнобедренный треугольник.
Задача №1
Здесь
и в дальнейшем строить изображение пирамиды будем согласно приведенному алгоритму.Строим основание пирамиды.
Равнобедренный треугольник изображается произвольным треугольником.
2. Строим высоту пирамиды.
По свойству пирамиды основание высоты – центр описанной около треугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
Одним из таких перпендикуляров будет медиана, проведенная к основанию треугольника.
На проекционном чертеже основание высоты занимает произвольное местоположение на проведенной медиане.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
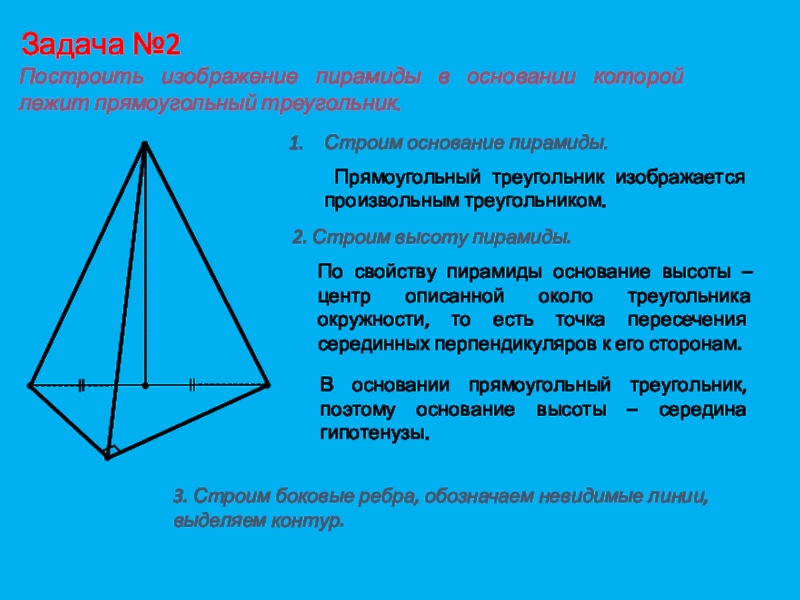
Слайд 17Задача №2
Построить изображение пирамиды в основании которой лежит прямоугольный треугольник.
Строим
основание пирамиды.Прямоугольный треугольник изображается произвольным треугольником.
2. Строим высоту пирамиды.
По свойству пирамиды основание высоты – центр описанной около треугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
В основании прямоугольный треугольник, поэтому основание высоты – середина гипотенузы.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
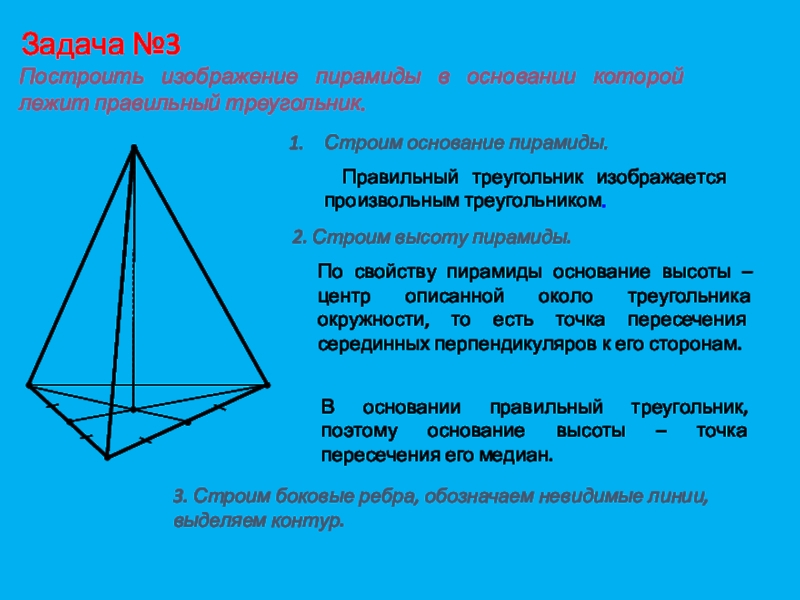
Слайд 18Задача №3
Построить изображение пирамиды в основании которой лежит правильный треугольник.
Строим
основание пирамиды.Правильный треугольник изображается произвольным треугольником.
2. Строим высоту пирамиды.
По свойству пирамиды основание высоты – центр описанной около треугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
В основании правильный треугольник, поэтому основание высоты – точка пересечения его медиан.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
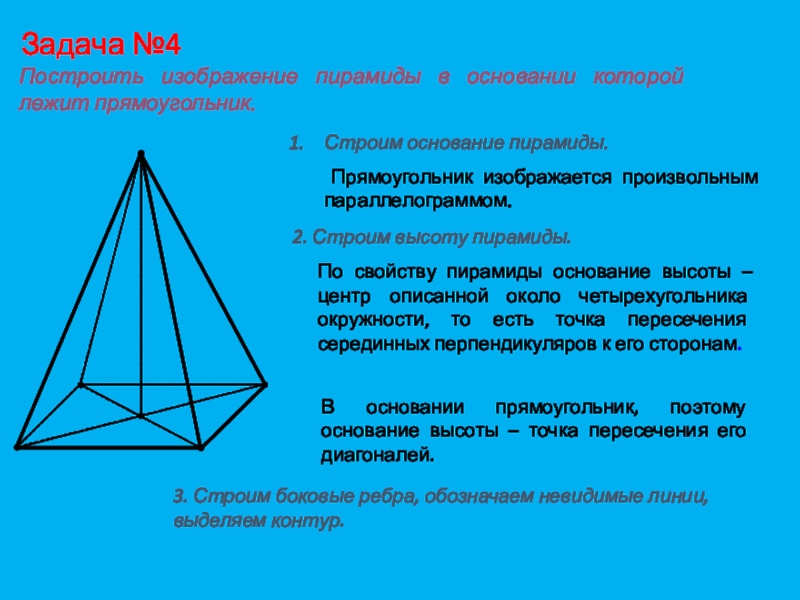
Слайд 19Задача №4
Построить изображение пирамиды в основании которой лежит прямоугольник.
Строим основание
пирамиды.Прямоугольник изображается произвольным параллелограммом.
2. Строим высоту пирамиды.
По свойству пирамиды основание высоты – центр описанной около четырехугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
В основании прямоугольник, поэтому основание высоты – точка пересечения его диагоналей.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
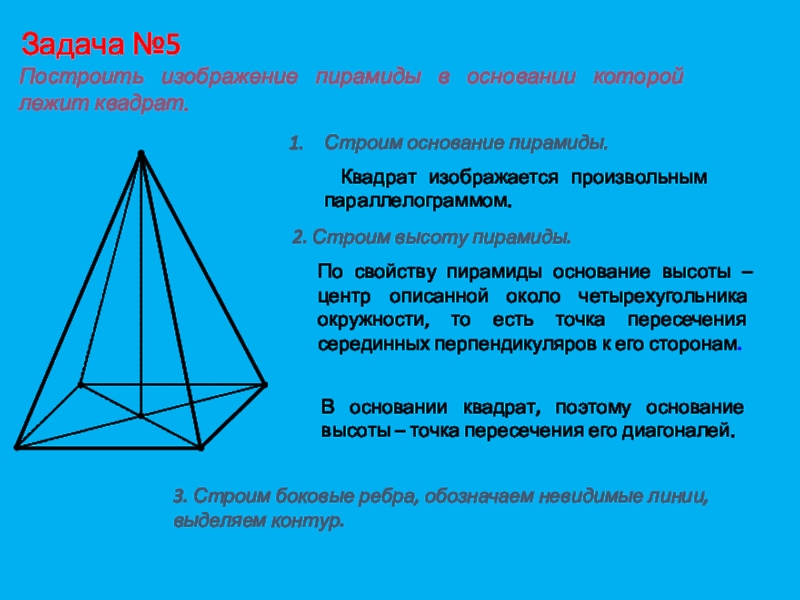
Слайд 20Задача №5
Построить изображение пирамиды в основании которой лежит квадрат.
Строим основание
пирамиды.Квадрат изображается произвольным параллелограммом.
2. Строим высоту пирамиды.
По свойству пирамиды основание высоты – центр описанной около четырехугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
В основании квадрат, поэтому основание высоты – точка пересечения его диагоналей.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
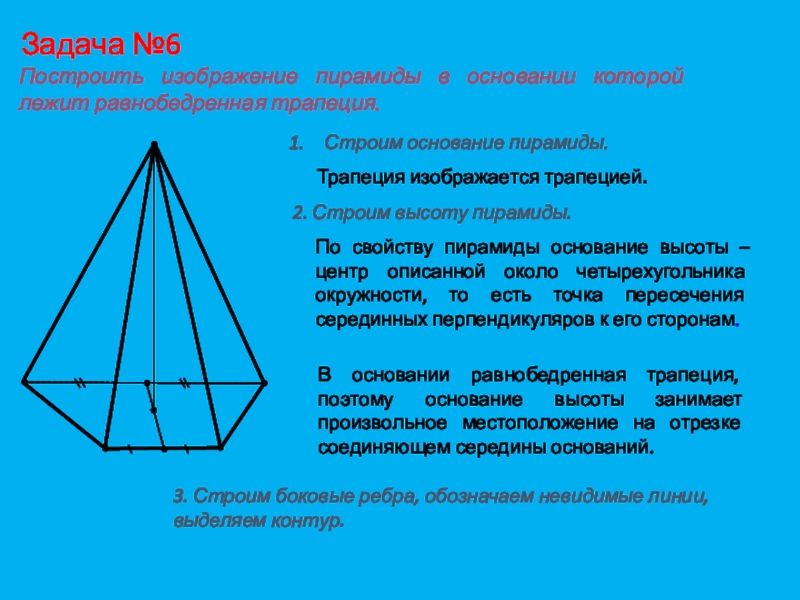
Слайд 21Задача №6
Построить изображение пирамиды в основании которой лежит равнобедренная трапеция.
Строим
основание пирамиды.Трапеция изображается трапецией.
2. Строим высоту пирамиды.
По свойству пирамиды основание высоты – центр описанной около четырехугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
В основании равнобедренная трапеция, поэтому основание высоты занимает произвольное местоположение на отрезке соединяющем середины оснований.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
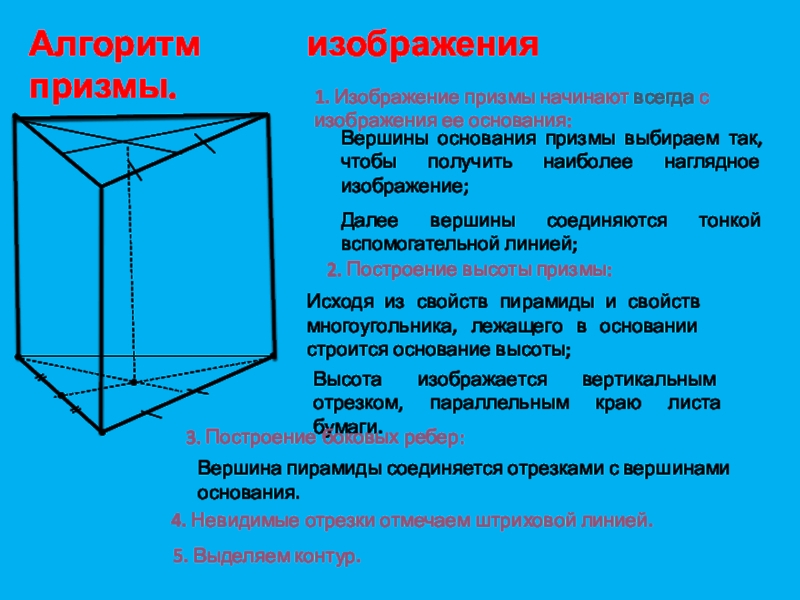
Слайд 22Алгоритм изображения призмы.
1. Изображение призмы начинают всегда с изображения ее
основания:
Вершины основания призмы выбираем так, чтобы получить наиболее наглядное изображение;
Далее
вершины соединяются тонкой вспомогательной линией;2. Построение высоты призмы:
Исходя из свойств пирамиды и свойств многоугольника, лежащего в основании строится основание высоты;
Высота изображается вертикальным отрезком, параллельным краю листа бумаги.
3. Построение боковых ребер:
Вершина пирамиды соединяется отрезками с вершинами основания.
4. Невидимые отрезки отмечаем штриховой линией.
5. Выделяем контур.
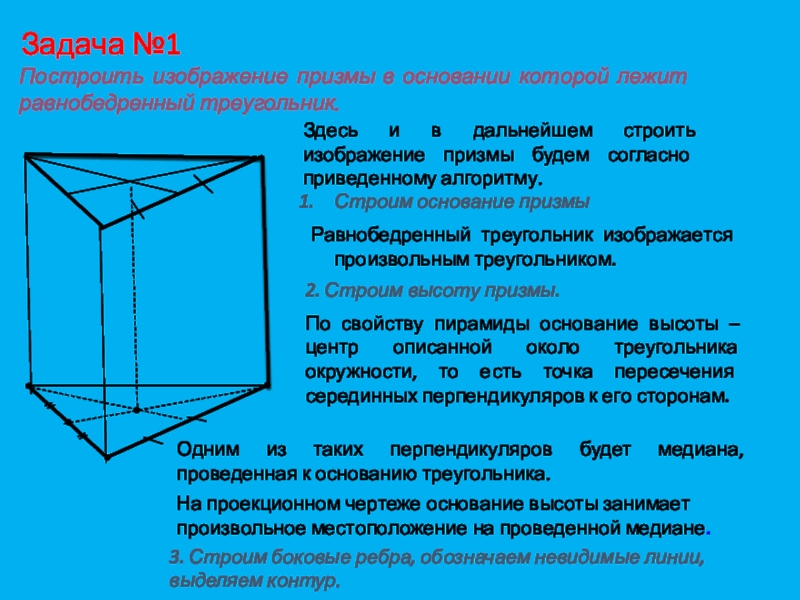
Слайд 23Построить изображение призмы в основании которой лежит равнобедренный треугольник.
Задача №1
Здесь
и в дальнейшем строить изображение призмы будем согласно приведенному алгоритму.Строим основание призмы
Равнобедренный треугольник изображается произвольным треугольником.
2. Строим высоту призмы.
По свойству пирамиды основание высоты – центр описанной около треугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
Одним из таких перпендикуляров будет медиана, проведенная к основанию треугольника.
На проекционном чертеже основание высоты занимает произвольное местоположение на проведенной медиане.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
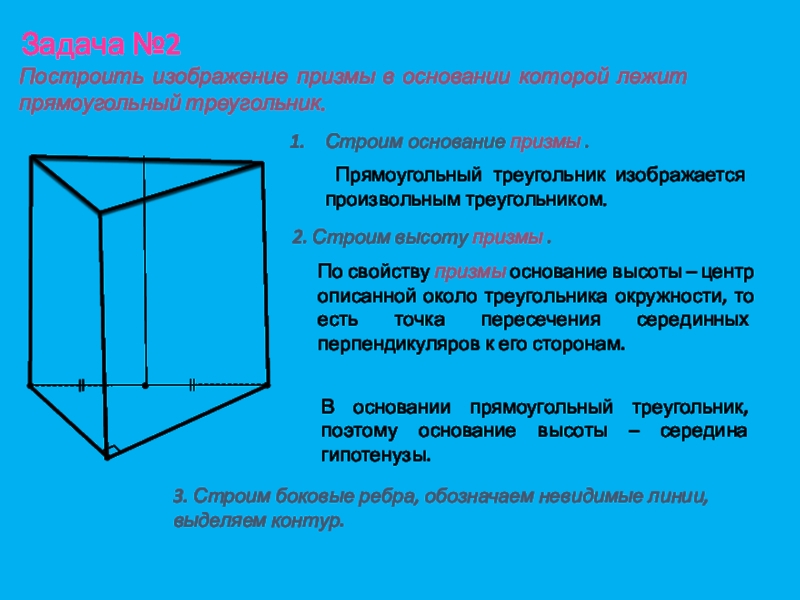
Слайд 24Задача №2
Построить изображение призмы в основании которой лежит прямоугольный треугольник.
Строим
основание призмы .Прямоугольный треугольник изображается произвольным треугольником.
2. Строим высоту призмы .
По свойству призмы основание высоты – центр описанной около треугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
В основании прямоугольный треугольник, поэтому основание высоты – середина гипотенузы.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
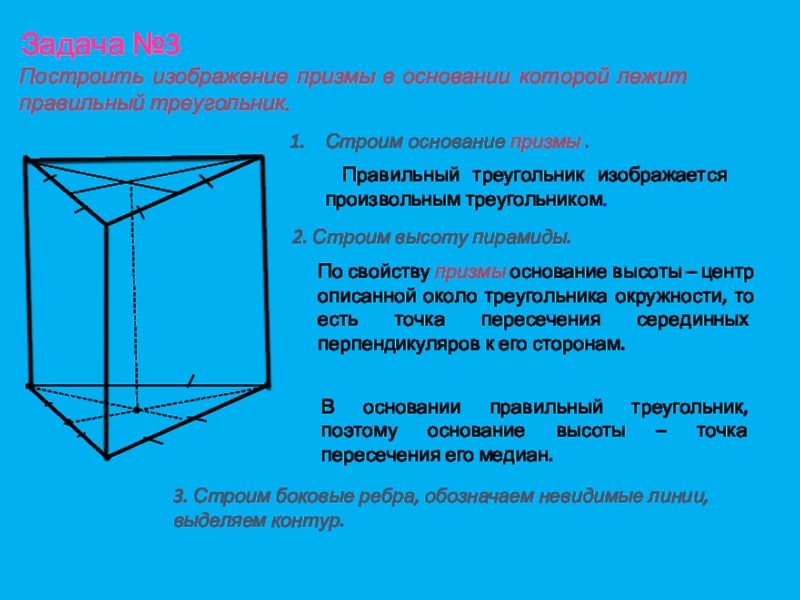
Слайд 25Задача №3
Построить изображение призмы в основании которой лежит правильный треугольник.
Строим
основание призмы .Правильный треугольник изображается произвольным треугольником.
2. Строим высоту пирамиды.
По свойству призмы основание высоты – центр описанной около треугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
В основании правильный треугольник, поэтому основание высоты – точка пересечения его медиан.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
Слайд 26Задача №4
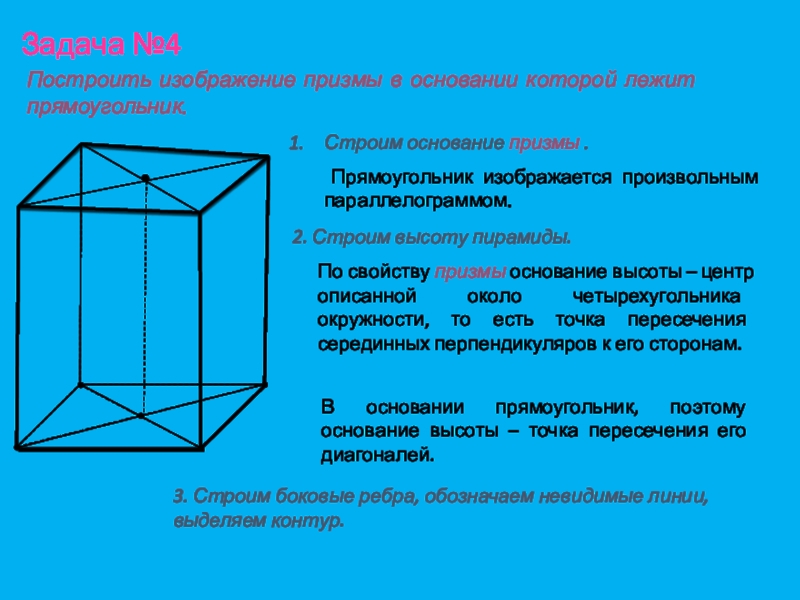
Построить изображение призмы в основании которой лежит прямоугольник.
Строим основание
призмы .Прямоугольник изображается произвольным параллелограммом.
2. Строим высоту пирамиды.
По свойству призмы основание высоты – центр описанной около четырехугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
В основании прямоугольник, поэтому основание высоты – точка пересечения его диагоналей.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
Слайд 27Задача №5
Построить изображение пирамиды в основании которой лежит квадрат.
Строим основание
пирамиды.Квадрат изображается произвольным параллелограммом.
2. Строим высоту пирамиды.
По свойству пирамиды основание высоты – центр описанной около четырехугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
В основании квадрат, поэтому основание высоты – точка пересечения его диагоналей.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
Слайд 28Задача №6
Построить изображение пирамиды в основании которой лежит равнобедренная трапеция.
Строим
основание пирамиды.Трапеция изображается трапецией.
2. Строим высоту пирамиды.
По свойству пирамиды основание высоты – центр описанной около четырехугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
В основании равнобедренная трапеция, поэтому основание высоты занимает произвольное местоположение на отрезке соединяющем середины оснований.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.