Тема: Продольные и поперечные деформации. Закон Гука. Цель урока: 1 ) Учебная:

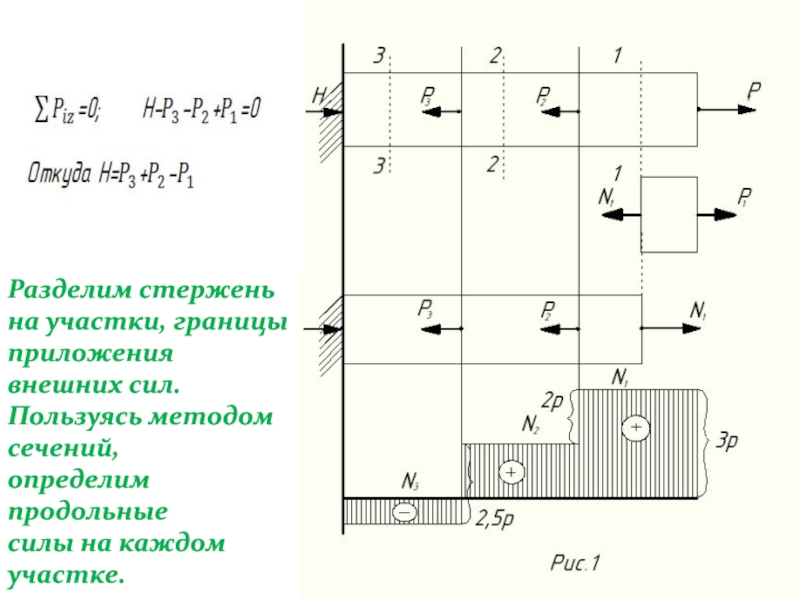
изучить понятия
продольной деформации; Закон Гука.
2) Воспитательная: развитие
познавательной активности,

интерес учащихся.
План урока:
1) Организационная часть
2) Актуализация прежних знаний
3) Изучение нового материала

бруса.
Центральным растяжением или
сжатием называется такой вид деформации,
при

котором в любом поперечном сечении
бруса возникает только продольная
(нормальная) сила N, а все остальные силовые
факторы равны 0. В случае растяжения
продольную силу N будем считать
положительной, при сжатии – отрицательной.
Изменение продольной силы по длине стержня
удобно представить в виде диаграммы, которая
называется эпюрой продольныx сил.

силами.
Построить эпюру продольных
сил для этого стержня.
РЕШЕНИЕ:
В защемлённом сечении
возникают

реакции Н,
которые можно определить
из уравнения равновесия.

сечений,
определим продольные
силы на каждом участке.

заключить, что все точки
какого-либо поперечного стержня
находятся в одинаковых

условиях, и,
условно, напряжения распределяются
по сечению равномерно. Эти напряжения параллельны продольной силе, т.е перпендикулярны поперечному сечению, а значит являются нормальными напряжениями.

законом Гука (английский
физик 1660 г.) и является основным
законом

сопротивления материалов.

упругости
– одна из важнейших физических
постоянных в материале. Она
характеризует

его жесткость,
т.е способность сопротивляться
упругому деформированию
(такие называют модулем Юнга.)

наз. изменение
первоначального положения сечения в результате деформации в брусе.

деформация.
Коэффициент Пуассона

ученого, который впервые ввёл этот к-т).
Для некоторых материалов :
Сталь 0,24

– 0,32
Медь 0,31 – 0,35
Бронза 0,32 – 0,35
Резина, каучук 0,47