Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ТЕМА.1 ЦЕЛЫЕ и РАЦИОНАЛЬНЫЕ ЧИСЛА. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. Преподаватель Гобова
Содержание
- 1. ТЕМА.1 ЦЕЛЫЕ и РАЦИОНАЛЬНЫЕ ЧИСЛА. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. Преподаватель Гобова
- 2. Содержание: Натуральные числа.Целые числа.Рациональные числаДействительные числаПреобразование выражений с действительными числами.
- 3. Для счета предметов используются числа , которые
- 4. Натуральные числа1, 2, 3, 4, 5, 6...
- 5. Целые числаЦелыми числами называют множество натуральных чисел,
- 6. Целые числа…-3;-2;-1;0,1, 2, 3,... m - целое
- 7. Отрицательные числа ввели в математический обиход Михаэль
- 8. Слайд 8
- 9. Рациональные числа Целые и дробные числа составляют
- 10. Рациональное число (лат. ratio
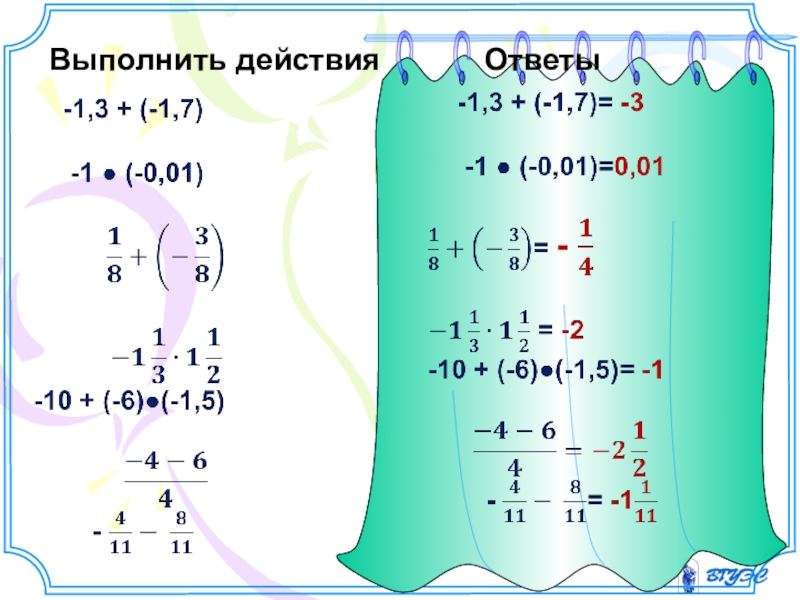
- 11. Выполнить действия Ответы
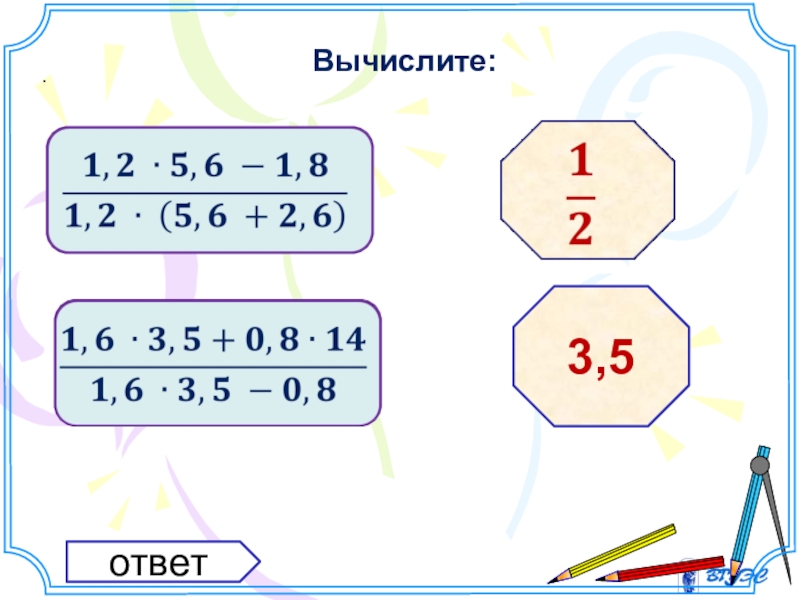
- 12. Вычислите:. ответ 3,5
- 13. Слайд 13
- 14. Дробные числа
- 15. Ничего, не зная об открытии ал –
- 16. Множество рациональных
- 17. Рациональные числа
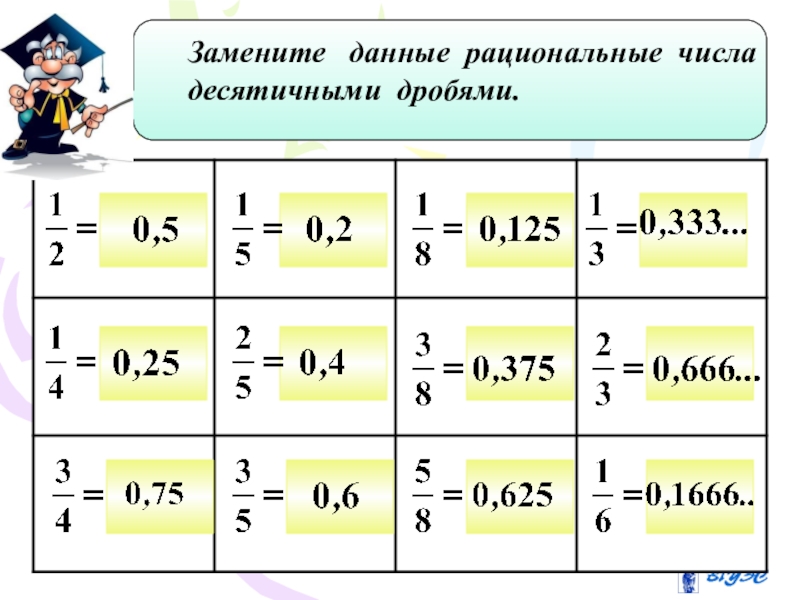
- 18. Замените данные рациональные числадесятичными дробями.
- 19. 0,(2)=291 цифра0,(81)=812 цифры99
- 20. Чтобы обратить смешанную периодическую дробь в обыкновенную,
- 21. Домашнее задание Записать в виде обыкновенной дроби бесконечную десятичную периодическую дробь.1,5(23)=0,3(18)=8,3(7) =1,(72)=2,9(12)=1,12(8)=
- 22. Вариант 11. Записать в виде
- 23. Скачать презентанцию
Содержание: Натуральные числа.Целые числа.Рациональные числаДействительные числаПреобразование выражений с действительными числами.
Слайды и текст этой презентации
Слайд 2Содержание:
Натуральные числа.
Целые числа.
Рациональные числа
Действительные числа
Преобразование выражений с действительными числами.
Слайд 5Целые числа
Целыми числами называют множество натуральных чисел, им противоположных и
число нуль.
Z=(1,2,3,4,5,6,7,8…
-1,-2,-3,-4,-5,-6,-7,-8…, 0)
Целые числа замкнуты относительны суммы, произведения и разности.
Слайд 7Отрицательные числа ввели
в математический обиход
Михаэль Штифель (1487—1567)
в книге
«Полная арифметика» (1544),
и Никола Шюке (1445—1500)-
его работа была
обнаружена в 1848 году.Слайд 9Рациональные числа
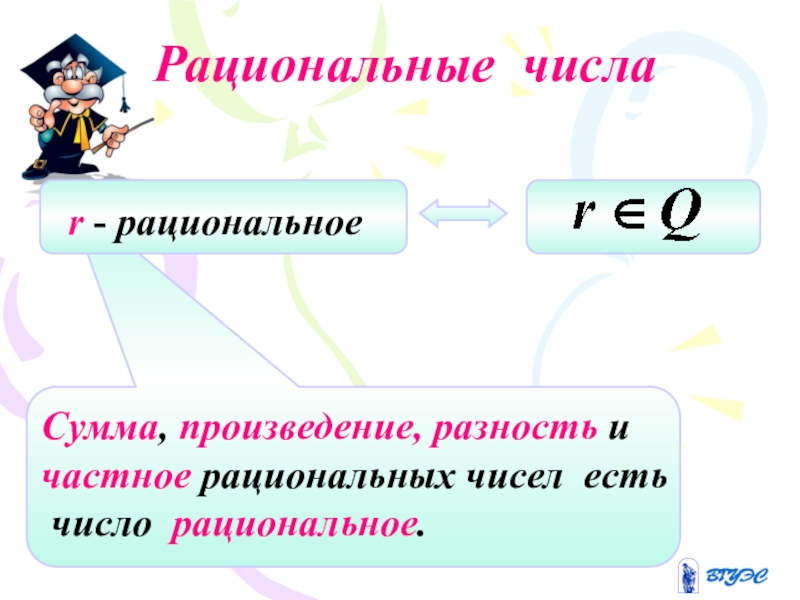
Целые и дробные числа составляют множество рациональных чисел.
Q=(целые
числа, дробные числа)
Рациональные числа замкнуты относительно суммы, разности, произведения и
частного (исключая деления на нуль)Слайд 10 Рациональное число (лат. ratio — отношение, деление,
дробь) — число, представляемое обыкновенной дробью , где числитель m
— целое число, а знаменатель n — натуральное число. Такую дробь следует понимать как результат деления m на n, даже если нацело разделить не удаётся.Слайд 15Ничего, не зная об открытии ал – Коши,
десятичные дроби открыл
второй раз,
приблизительно через 150 лет, после него,
фламандский ученый
математик и инженерСимон Стевин в труде «Децималь» (1585 г).
Слайд 16 Множество рациональных чисел
Множество
рациональных чисел обозначается и может быть записано в виде: Q=m:n
Нужно понимать, что численно равные дроби такие как, например, 3/4 и 9/12 , входят в это множество как одно число.
Поскольку делением числителя и знаменателя дроби на их наибольший общий делитель можно получить единственное несократимое представление рационального числа, то можно говорить об их множестве как о множестве несократимых дробей со взаимно простыми целым числителем и натуральным знаменателем:
Слайд 20Чтобы обратить смешанную периодическую дробь
в обыкновенную, нужно в числителе
обыкновенной дроби
поставить число, равное разности числа, образованного цифрами,
стоящими после запятой до начала второго периода, и числа, образованного из цифр, стоящих после запятой до начала первого периода; а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, и со столькими нулями, сколько цифр между запятой и началом периода.
0,4(6)=
4
6
4
1 цифра
9
1 цифра
0
Слайд 21
Домашнее задание
Записать в виде обыкновенной дроби бесконечную десятичную периодическую дробь.
1,5(23)=
0,3(18)=
8,3(7)
=
1,(72)=
2,9(12)=
1,12(8)=
Слайд 22Вариант 1
1. Записать в виде
а)
б)
2.Представьте в виде
а) 15,(3)
б) 2,(14)
в)
1,6(1)Вариант 2
бесконечной дроби
а) б)
обыкновенной дроби
а) 7,(2)
б) 23,(25)
в) 3,9(12)
Самостоятельная работа