Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тензор деформаций. Тензор скоростей деформации
Содержание
- 1. Тензор деформаций. Тензор скоростей деформации
- 2. Тензор скоростей деформацииНапряжённое состояние среды связано и
- 3. Тензор скоростей деформацииСвязь напряжений и деформаций для
- 4. Тензор скоростей деформацииТензор напряжений (или напряжённое состояние
- 5. Тензор скоростей деформацииНапряжения, их величина, в вязкой,
- 6. Тензор скоростей деформацииВ общем случае течения, возможно,
- 7. Тензор скоростей деформации
- 8. Тензор скоростей деформацииДвижение жидкости представляет собой одновременное
- 9. Тензор скоростей деформацииТензор скоростей деформаций вводится следующим
- 10. Тензор скоростей деформацииУравнениями состояния или реологическими уравнениями
- 11. Тензор деформацииНапряжения приложенные к среде (возникающие в
- 12. Тензор деформацииВырежем из тела (полимера) элементарный параллелепипед
- 13. Тензор деформацииВ результате деформации тела выделенный параллелепипед
- 14. Тензор деформацииСпроецируем первоначальное положение грани АВСД и
- 15. Тензор деформацииПри этом ребро АД, которое до
- 16. Тензор деформацииОтносительная линейная деформация в направлении х:
- 17. Тензор деформацииРассмотрим отдельно угловую деформацию. Пусть грань
- 18. Тензор деформацииПри этом т. Д перемещается в
- 19. Тензор деформацииТ.к. углы малы, то их величины
- 20. Тензор деформацииУгловая деформация на плоскости Аху будет равна:Аналогично получаем деформацию для плоскостей хАz и уАz:
- 21. Тензор деформацииВ итоге получаем шесть независимых компонент линейных и угловых деформаций.Тензор деформации выводим следующим образом:
- 22. Тензор деформацииТензор симметричен, т.е.В случае упругой деформации существуют следующие зависимости тензоров напряжений и деформаций.
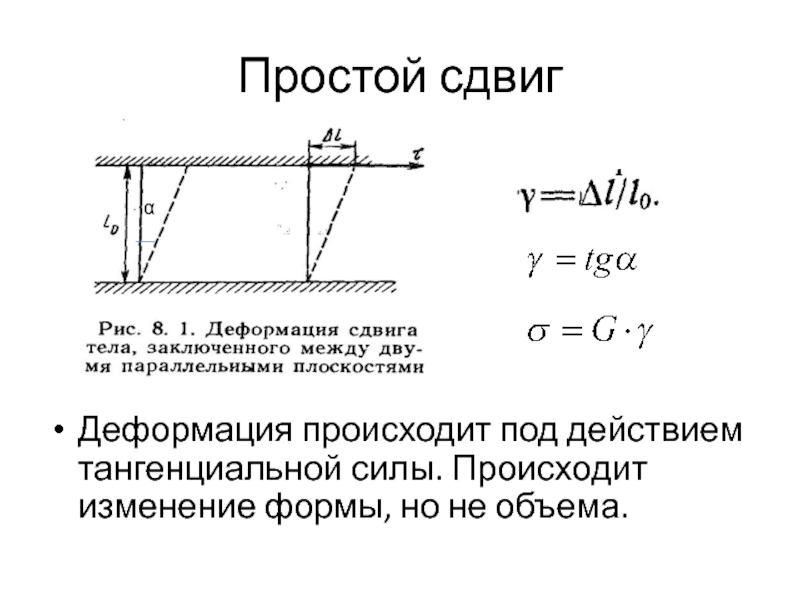
- 23. Простой сдвигДеформация происходит под действием тангенциальной силы. Происходит изменение формы, но не объема.α
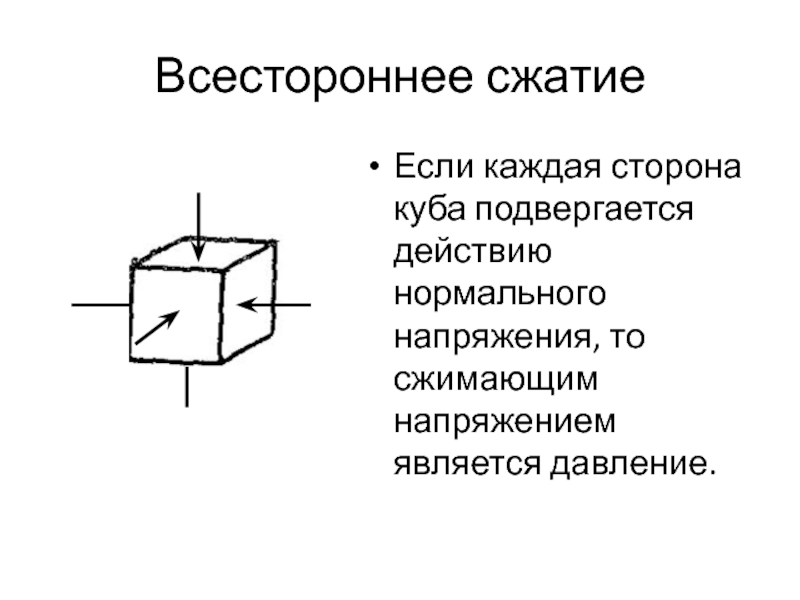
- 24. Всестороннее сжатиеЕсли каждая сторона куба подвергается действию нормального напряжения, то сжимающим напряжением является давление.
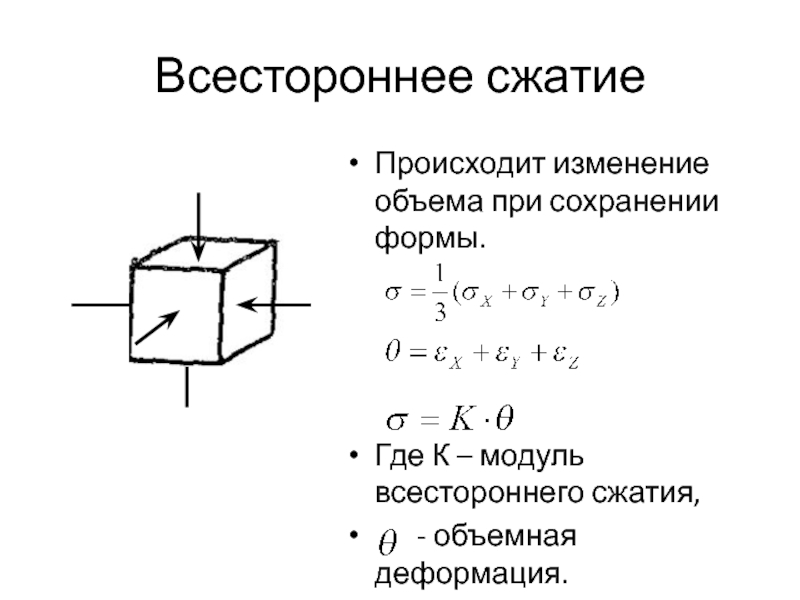
- 25. Всестороннее сжатиеПроисходит изменение объема при сохранении формы.Где
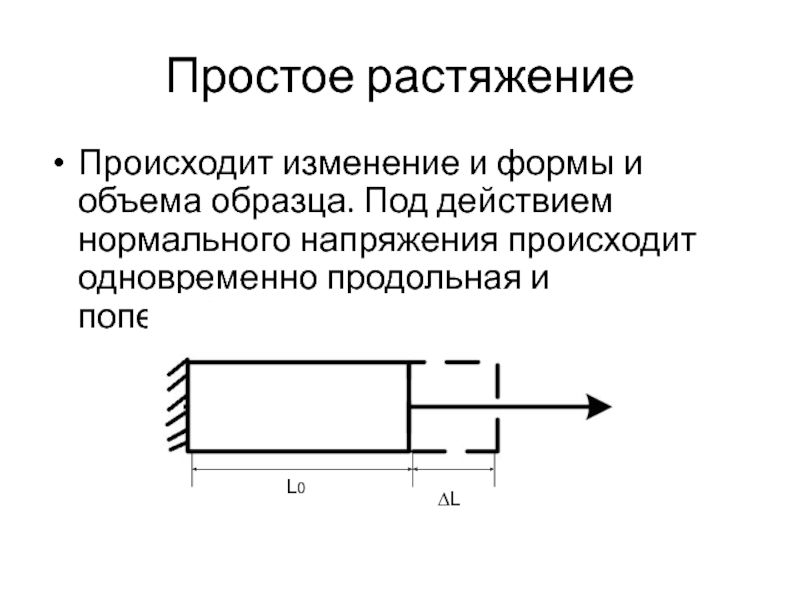
- 26. Простое растяжениеПроисходит изменение и формы и объема
- 27. Простое растяжениеПо закону Гука:Где Е – модуль
- 28. Простое растяжениеУравнение связывающее константы:При
- 29. Тензор деформацииЕсли деформация строго пропорциональна напряжению, то
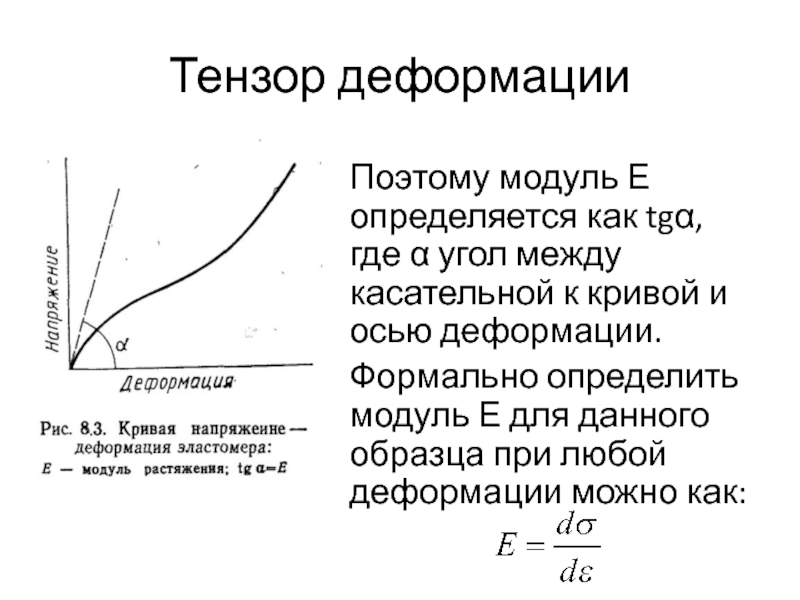
- 30. Тензор деформацииПоэтому модуль Е определяется как tgα,
- 31. Спасибо за внимание
- 32. Скачать презентанцию
Тензор скоростей деформацииНапряжённое состояние среды связано и определяется деформационными изменениями. Так, например, под воздействием одной и той же растягивающей силы различные материалы получают различные удлинения.
Слайды и текст этой презентации
Слайд 2Тензор скоростей деформации
Напряжённое состояние среды связано и определяется деформационными изменениями.
Слайд 3Тензор скоростей деформации
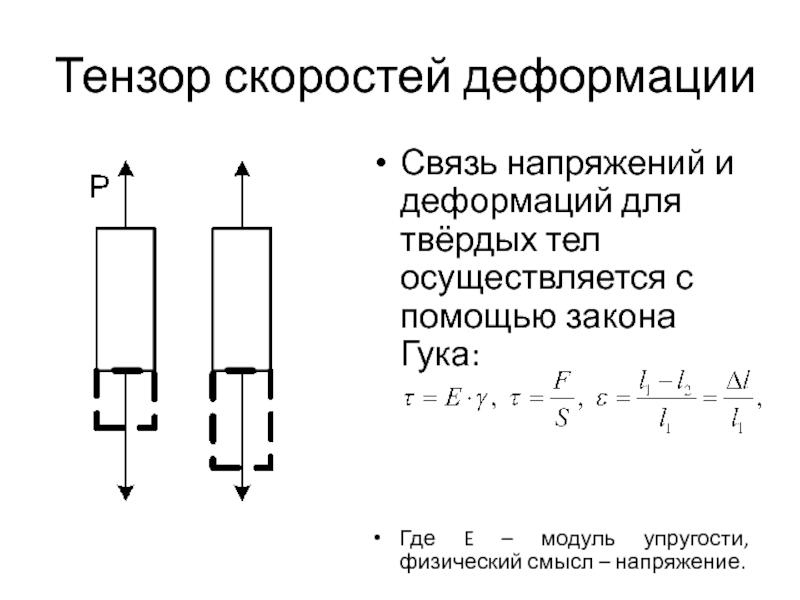
Связь напряжений и деформаций для твёрдых тел осуществляется
с помощью закона Гука:
Где E – модуль упругости, физический смысл
– напряжение.
Слайд 4Тензор скоростей деформации
Тензор напряжений (или напряжённое состояние точки среды) зависит
от скорости течения среды.
Кинематическое соотношение, характеризующее
движение жидкости - это градиент скорости . 
Слайд 5Тензор скоростей деформации
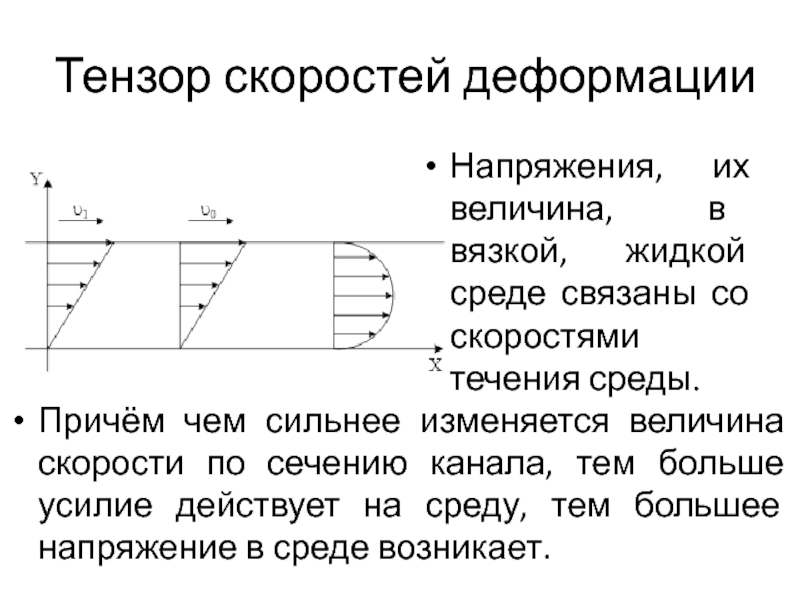
Напряжения, их величина, в вязкой, жидкой среде связаны
со скоростями течения среды.
Причём чем сильнее изменяется величина скорости по
сечению канала, тем больше усилие действует на среду, тем большее напряжение в среде возникает.
Слайд 6Тензор скоростей деформации
В общем случае течения, возможно, более чем одно
ненулевое направление градиента скорости.
Каждый из трёх компонентов скорости может
изменяться в трёх координатных направлениях, что даёт девять возможных компонент градиента. Таким образом, можно ввести тензор градиентов скорости , который в декартовых координатах запишется:
Слайд 8Тензор скоростей деформации
Движение жидкости представляет собой одновременное перемещение и вращение.
Такие движения можно разделить, представить тензор градиентов деформацией в виде
двух частей:Где γ - тензор скоростей деформации, ω - вращательный тензор.
Слайд 9Тензор скоростей деформации
Тензор скоростей деформаций вводится следующим образом:
где
тензор - транспонированный тензор, имеющий те же компоненты, что и
, но с переставленными индексами (столбцы и строки переставлены).
Слайд 10Тензор скоростей деформации
Уравнениями состояния или реологическими уравнениями называют уравнения связывающие
тензор напряжений и тензор скоростей деформаций, т.е.
Слайд 11Тензор деформации
Напряжения приложенные к среде (возникающие в среде) приводят к
возникновению различного рода деформаций. Течению – для жидкой среды, изменению
объема и формы тел.Для определения полного деформационного состояния в среде вводят понятие тензора деформаций.
Слайд 12Тензор деформации
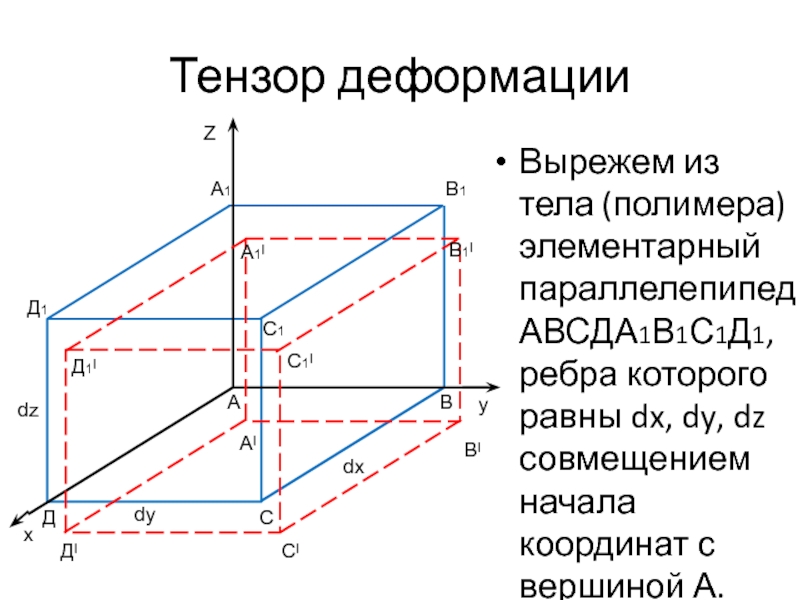
Вырежем из тела (полимера) элементарный параллелепипед АВСДА1В1С1Д1, ребра которого
равны dx, dy, dz совмещением начала координат с вершиной А.
А
В
Д
С
Z
y
x
А1
Д1
В1
С1
Дᴵ
Сᴵ
Вᴵ
Аᴵ
Д1ᴵ
А1ᴵ
В1ᴵ
С1ᴵ
dz
dy
dx
Слайд 13Тензор деформации
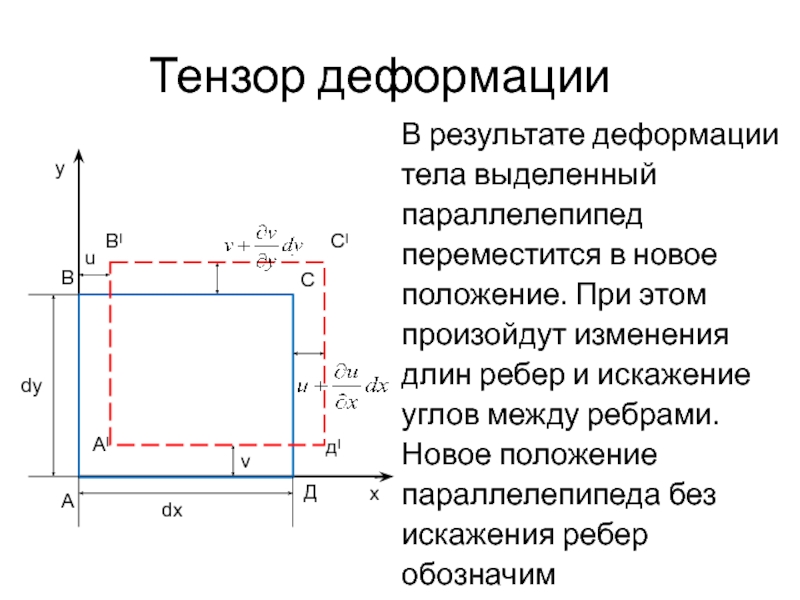
В результате деформации тела выделенный параллелепипед переместится в новое
положение. При этом произойдут изменения длин ребер и искажение углов
между ребрами.Новое положение параллелепипеда без искажения ребер обозначим А`В`С`Д`А1`В1`С1`Д1`.
y
x
A
B
C
Д
dy
dx
u
v
Aᴵ
дᴵ
Вᴵ
Сᴵ
Слайд 14Тензор деформации
Спроецируем первоначальное положение грани АВСД и новое положение этой
грани на плоскость хАу. Обозначим линейные перемещения т. А в
направлении осей х и у через u и v. Линейное перемещение т. С в направлении оси х равно:В направлении оси у равно:
Слайд 15Тензор деформации
При этом ребро АД, которое до деформации имело длину
dx получит приращение равное ,
а ребро АВ, которое до деформации имело длину dy увеличится на .Относительной линейной деформацией в точке по данному направлению называется отношение изменения длины бесконечно малого линейного элемента к его первоначальной длине.
Слайд 16Тензор деформации
Относительная линейная деформация в направлении х:
Для направления y:
Аналогично, если рассмотреть другую проекцию
граней:
Где линейное приращение т. А в направлении оси z.
Слайд 17Тензор деформации
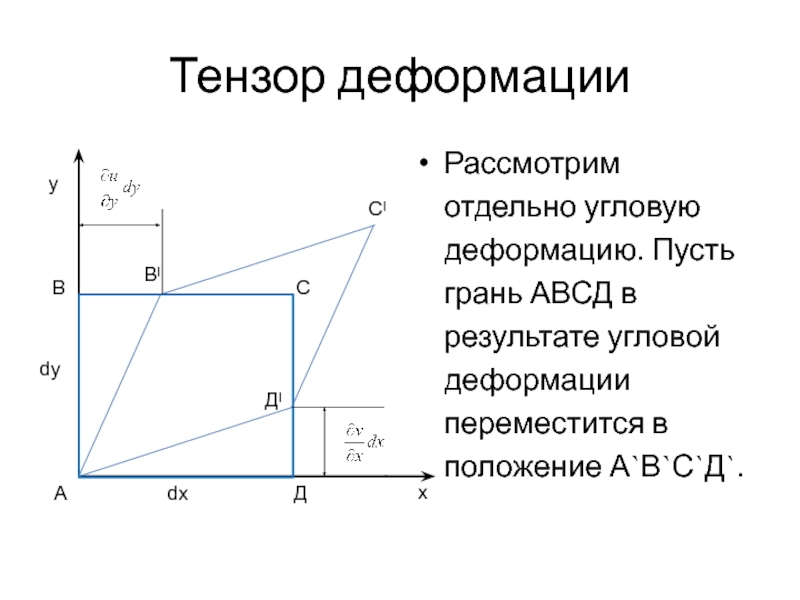
Рассмотрим отдельно угловую деформацию. Пусть грань АВСД в результате
угловой деформации переместится в положение А`В`С`Д`.
y
x
B
Bᴵ
Cᴵ
C
А
Д
Дᴵ
dx
dy
Слайд 18Тензор деформации
При этом т. Д перемещается в направлении у в
т. Д`, перемещение при этом
.т. В – в направлении х в т. В`, перемещение при этом равно:
Угловой деформацией называется величина искажения прямого угла, т.е.
γxy=π/2- BᴵАДᴵ= ВАВᴵ+ ДАДᴵ
Слайд 19Тензор деформации
Т.к. углы малы, то их величины можно заменить тангенсами
этих углов, т.е. принимаем, что:
ДАДᴵ=ДДᴵ/АД=
Слайд 20Тензор деформации
Угловая деформация на плоскости Аху будет равна:
Аналогично получаем деформацию
для плоскостей хАz и уАz:
Слайд 21Тензор деформации
В итоге получаем шесть независимых компонент линейных и угловых
деформаций.
Тензор деформации выводим следующим образом:
Слайд 22Тензор деформации
Тензор симметричен, т.е.
В случае упругой деформации существуют следующие зависимости
тензоров напряжений и деформаций.
Слайд 23Простой сдвиг
Деформация происходит под действием тангенциальной силы. Происходит изменение формы,
но не объема.
α
Слайд 24Всестороннее сжатие
Если каждая сторона куба подвергается действию нормального напряжения, то
сжимающим напряжением является давление.
Слайд 25Всестороннее сжатие
Происходит изменение объема при сохранении формы.
Где К – модуль
всестороннего сжатия,
- объемная деформация.
Слайд 26Простое растяжение
Происходит изменение и формы и объема образца. Под действием
нормального напряжения происходит одновременно продольная и поперечная деформации.
L0
∆L
Слайд 27Простое растяжение
По закону Гука:
Где Е – модуль Юнга, модуль упругости.
Коэффициент
Пуассона:
Характеризует соотношение продольной и поперечной деформаций.
Слайд 29Тензор деформации
Если деформация строго пропорциональна напряжению, то модуль Е есть
коэффициент пропорциональности и имеет для заданного материала определенное значение. В
общем случае пропорциональность напряжения и деформации отсутствует.
Слайд 30Тензор деформации
Поэтому модуль Е определяется как tgα, где α угол
между касательной к кривой и осью деформации.
Формально определить модуль Е
для данного образца при любой деформации можно как:
