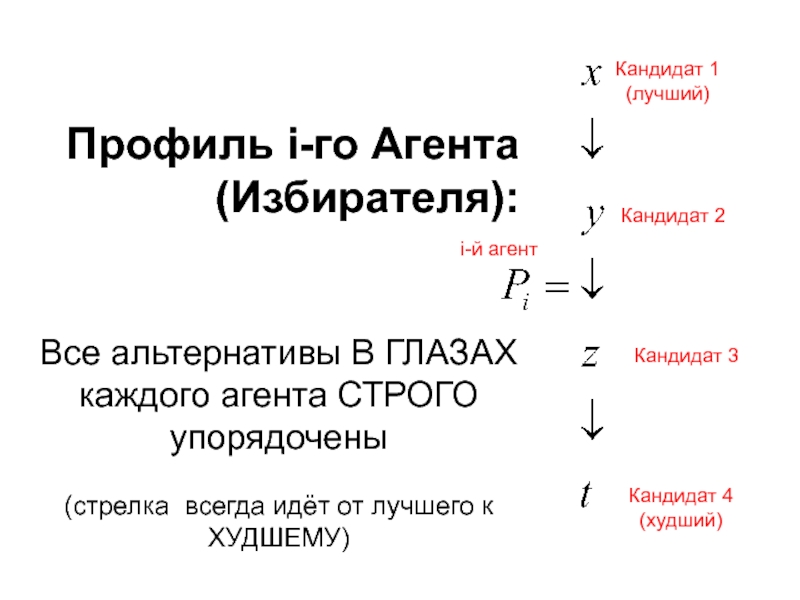
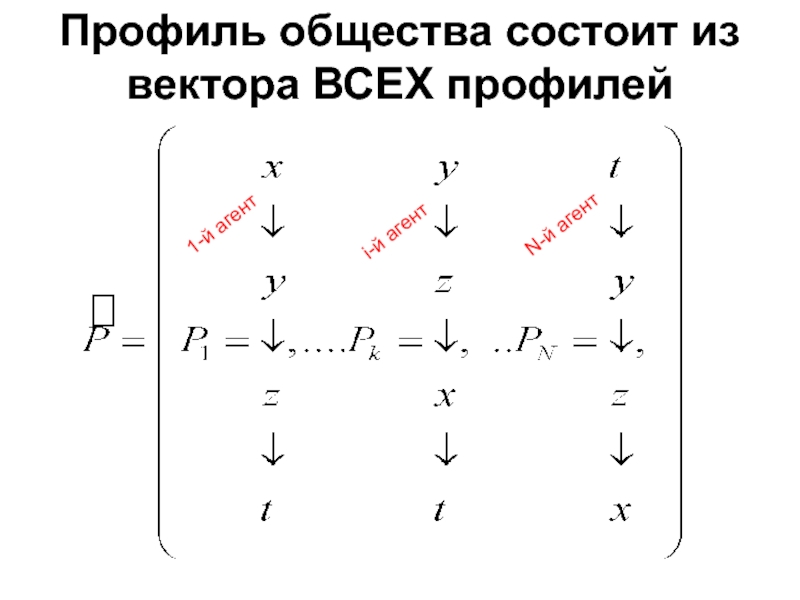
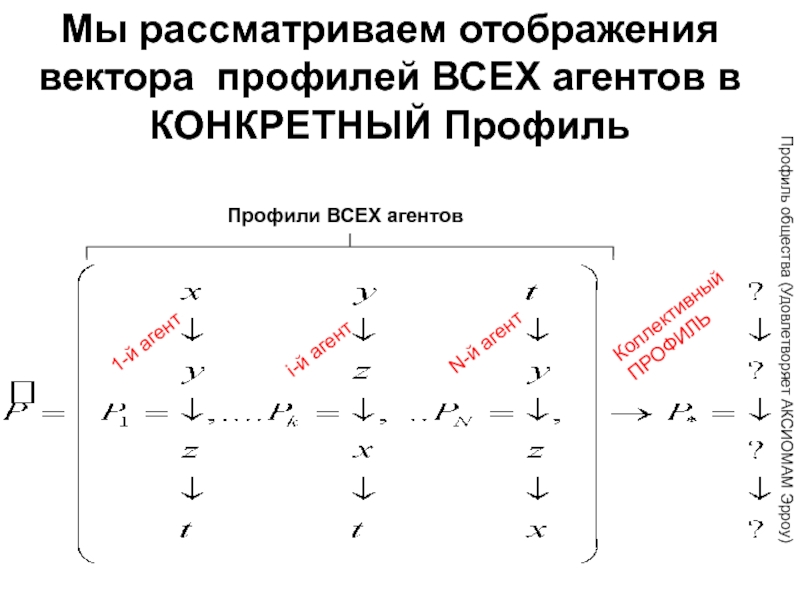
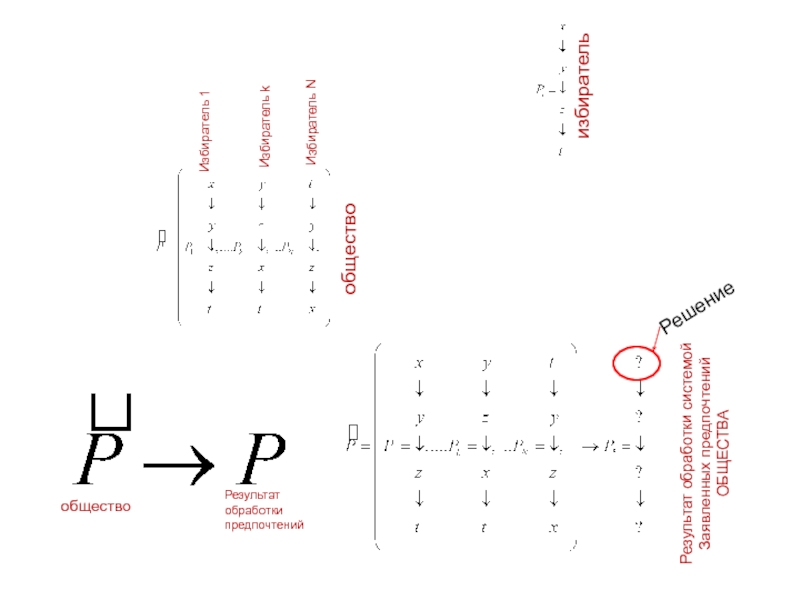
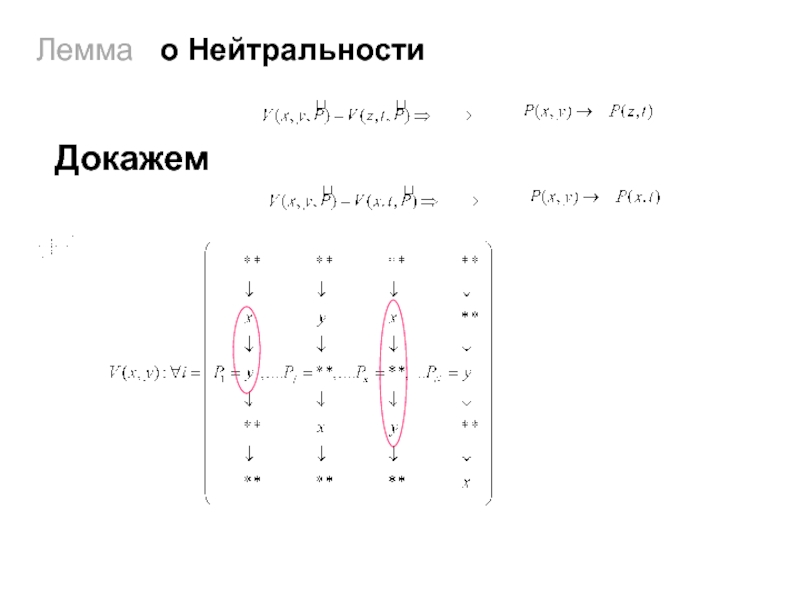
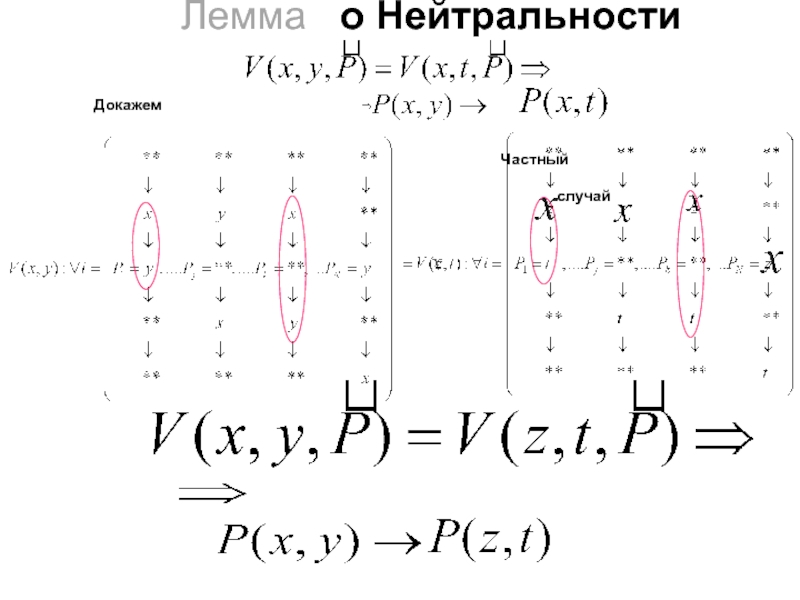
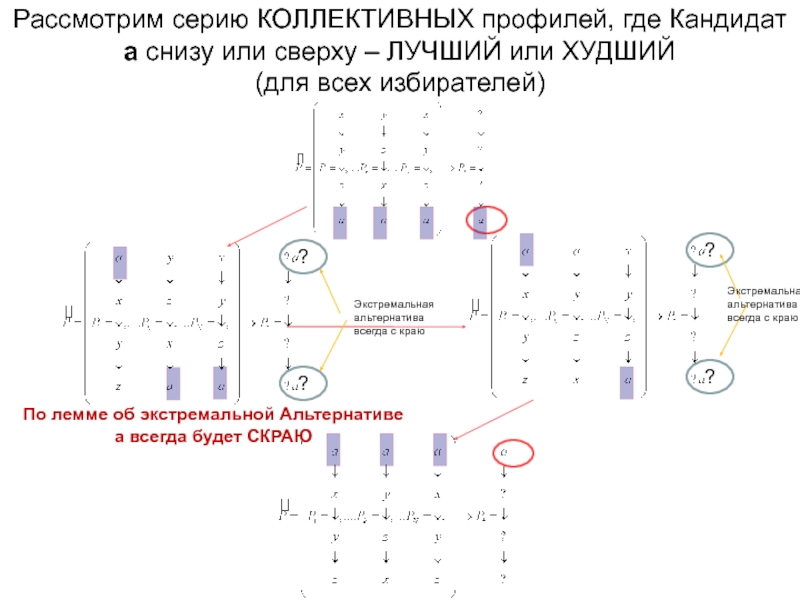
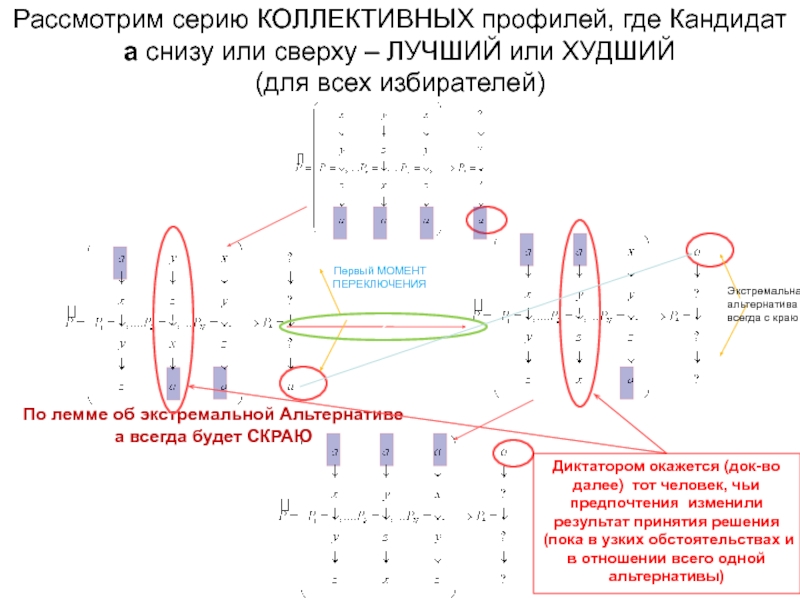
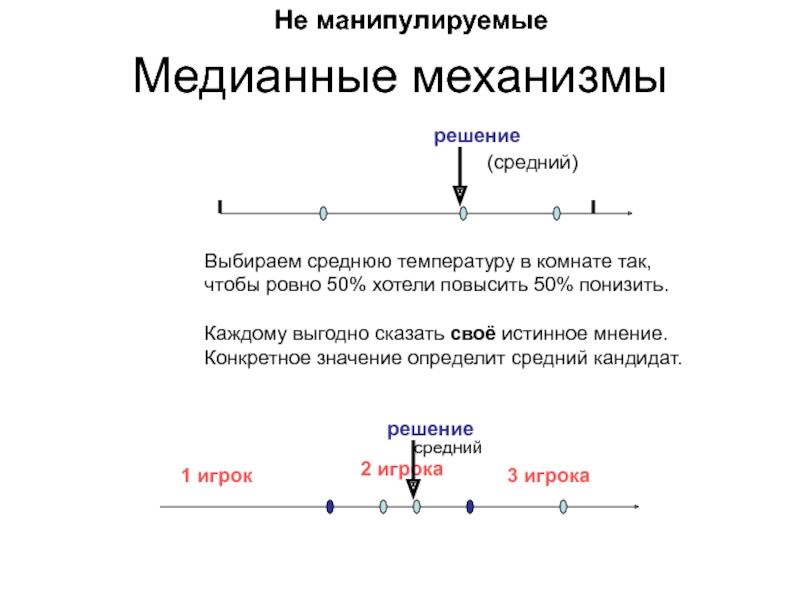
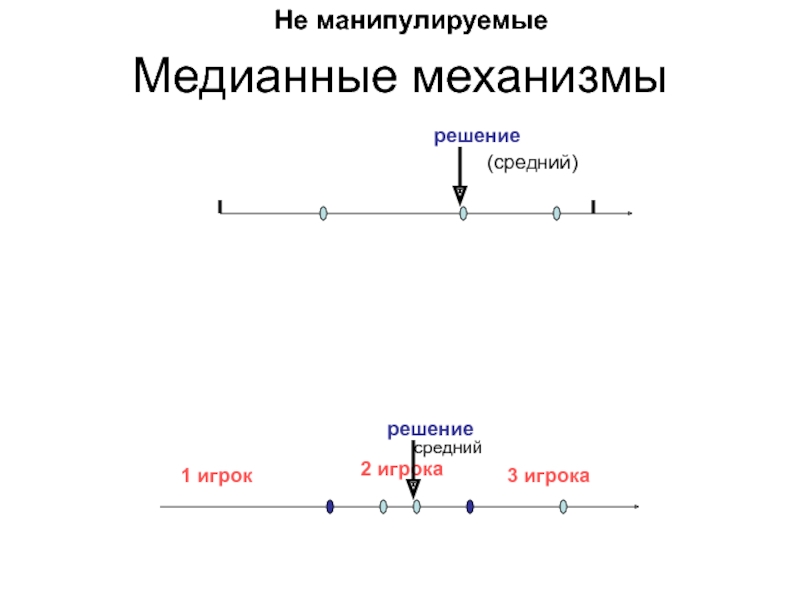
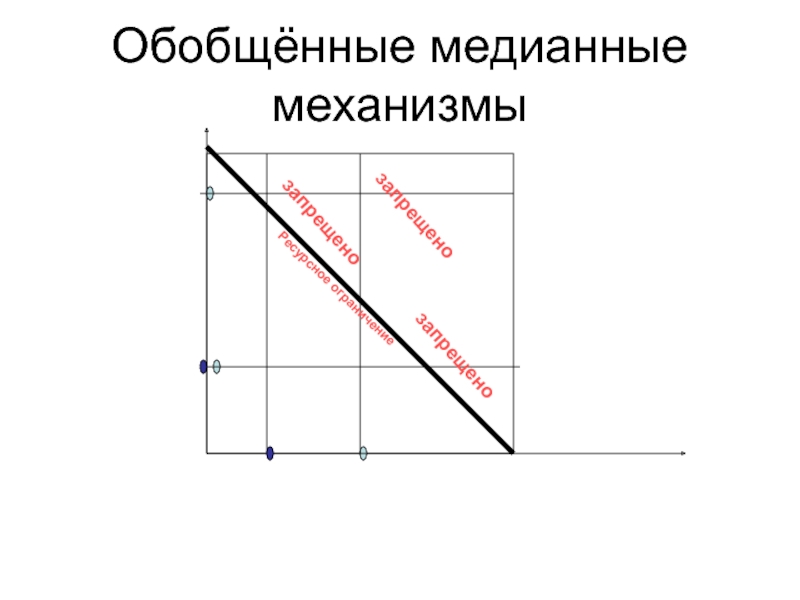
С
1
1
1
A и С
1
11
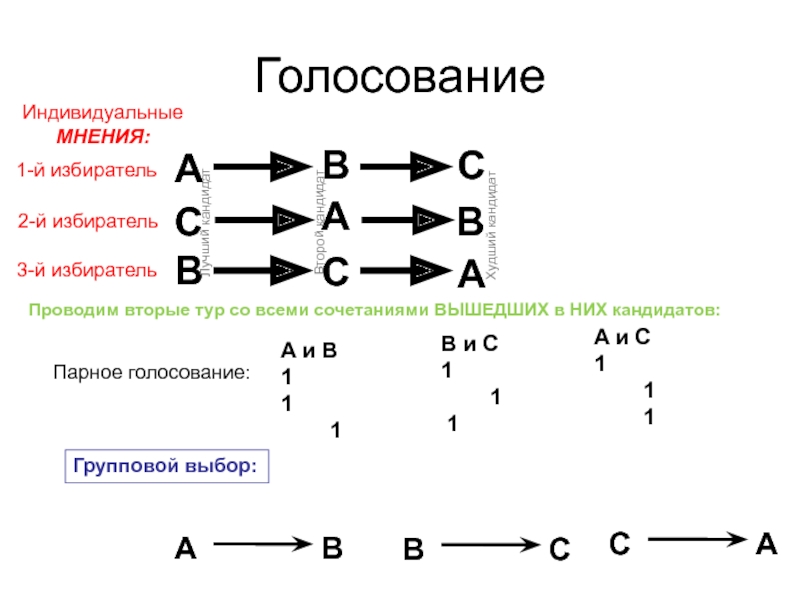
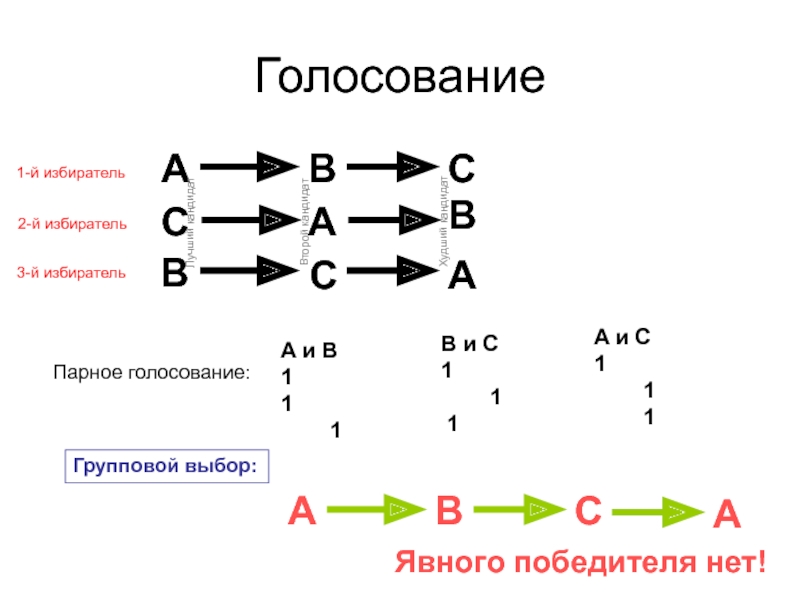
Парное голосование:
Групповой выбор:
B
A
C
B
A
C
1-й избиратель
2-й избиратель
3-й избиратель
Худший кандидат
Лучший кандидат
Второй кандидат
Индивидуальные
МНЕНИЯ:
Проводим вторые тур со всеми сочетаниями ВЫШЕДШИХ в НИХ кандидатов: