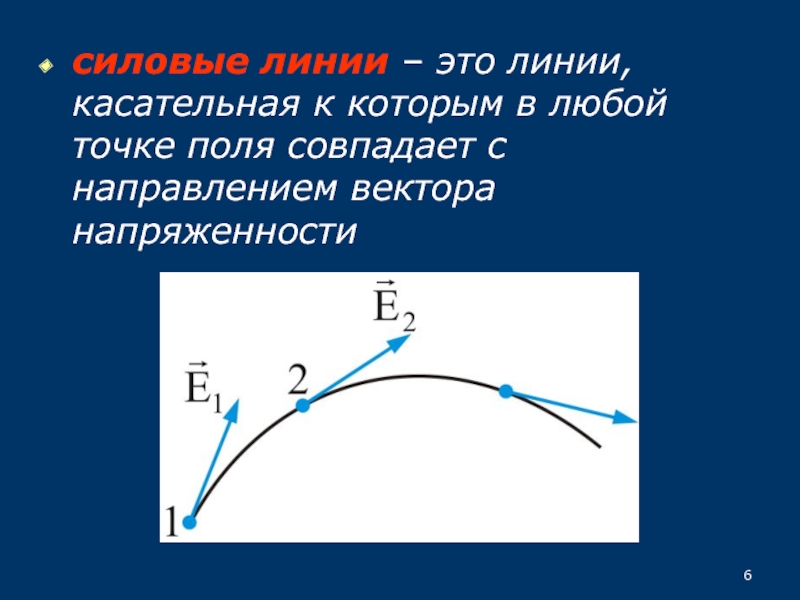
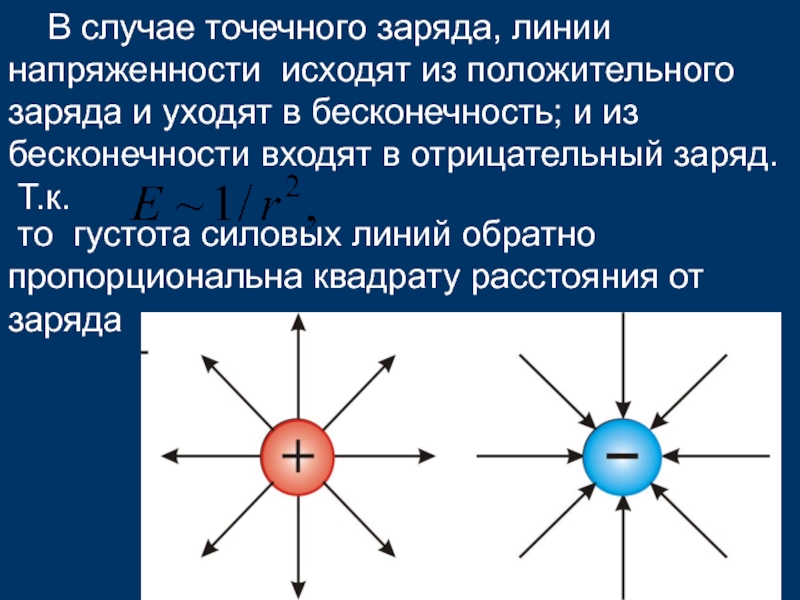
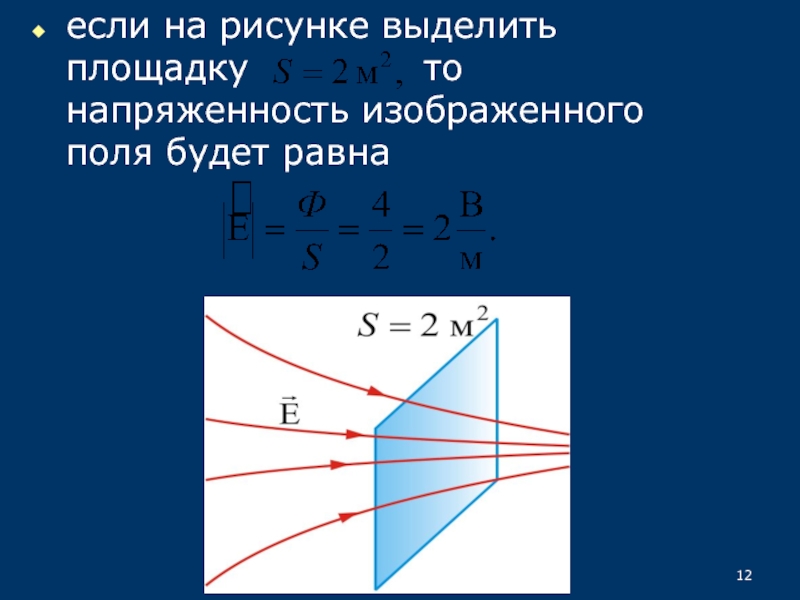
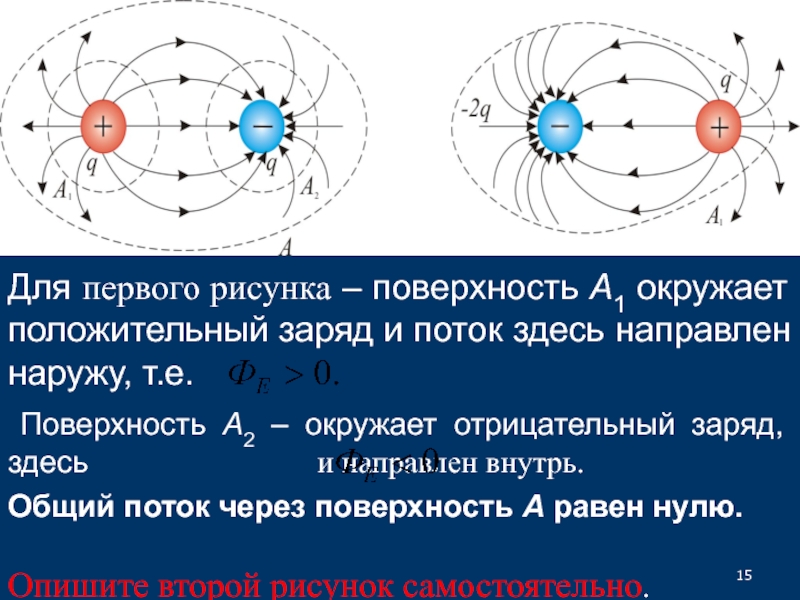
напряженности
33.3. Теорема Остроградского-Гаусса
33.4. Дифференциальная форма теоремы3.4. Дифференциальная форма теоремы 3.4.
Дифференциальная форма теоремы Остроградского-Гаусса33.5. Вычисление электростатических полей с помощью теоремы Остроградского3.5. Вычисление электростатических полей с помощью теоремы Остроградского 3.5. Вычисление электростатических полей с помощью теоремы Остроградского -3.5. Вычисление электростатических полей с помощью теоремы Остроградского - 3.5. Вычисление электростатических полей с помощью теоремы Остроградского - Гаусса
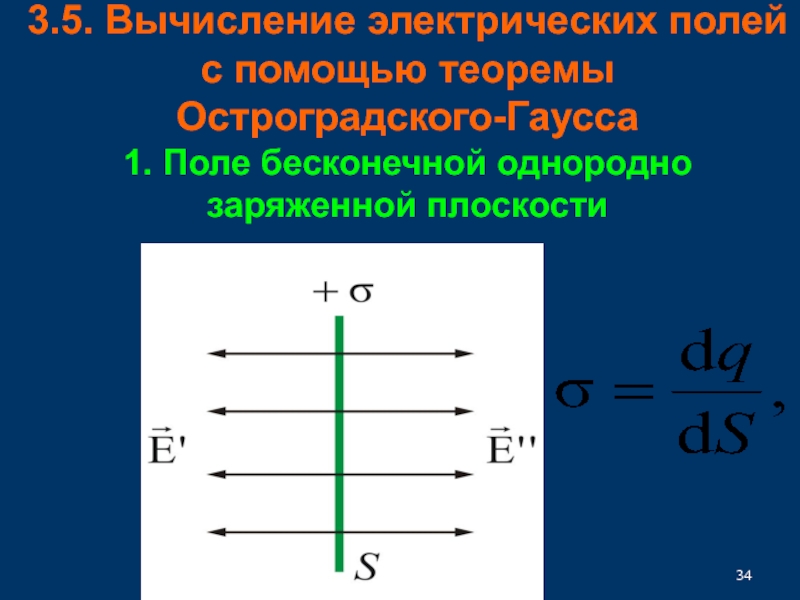
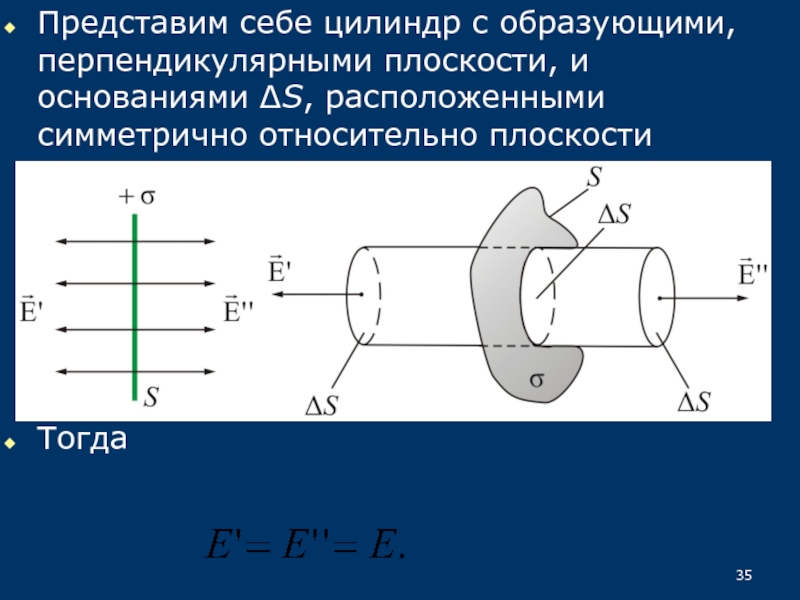
33.5.1. Поле бесконечной однородно заряженной плоскости
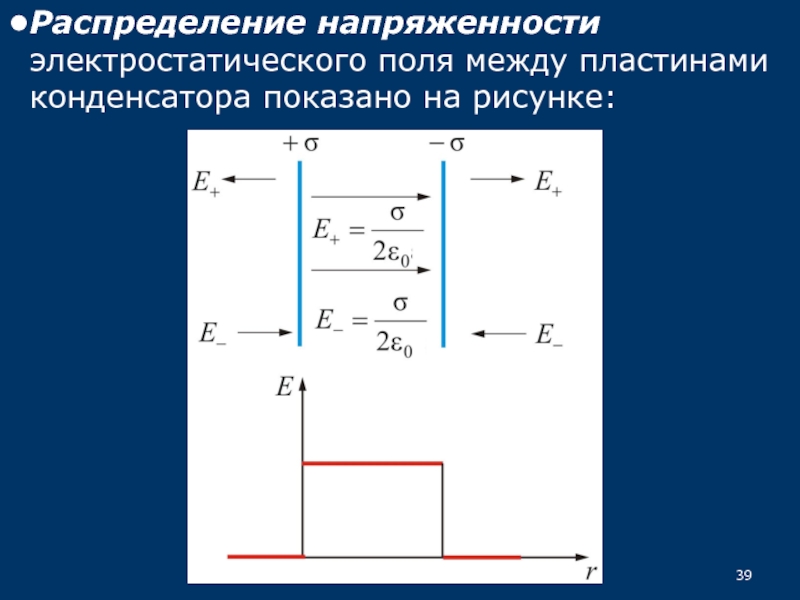
33.5.2. Поле двух равномерно заряженных плоскостей
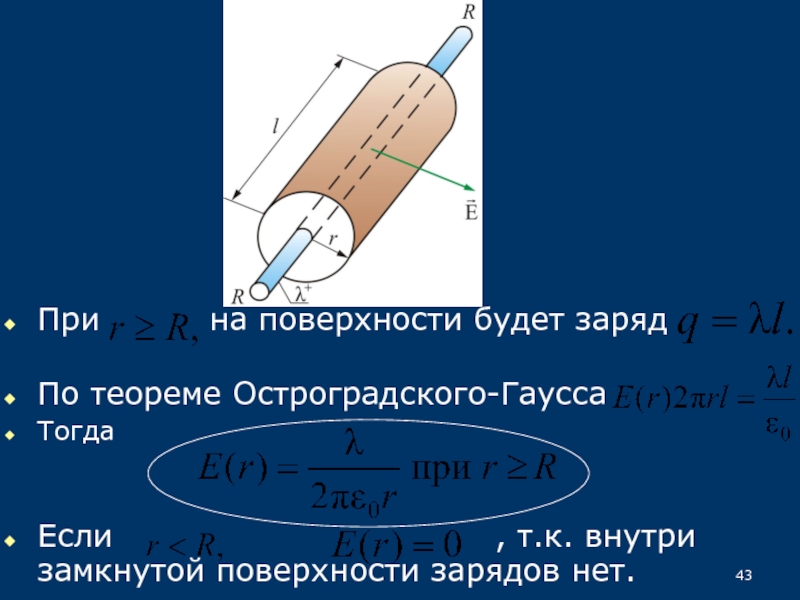
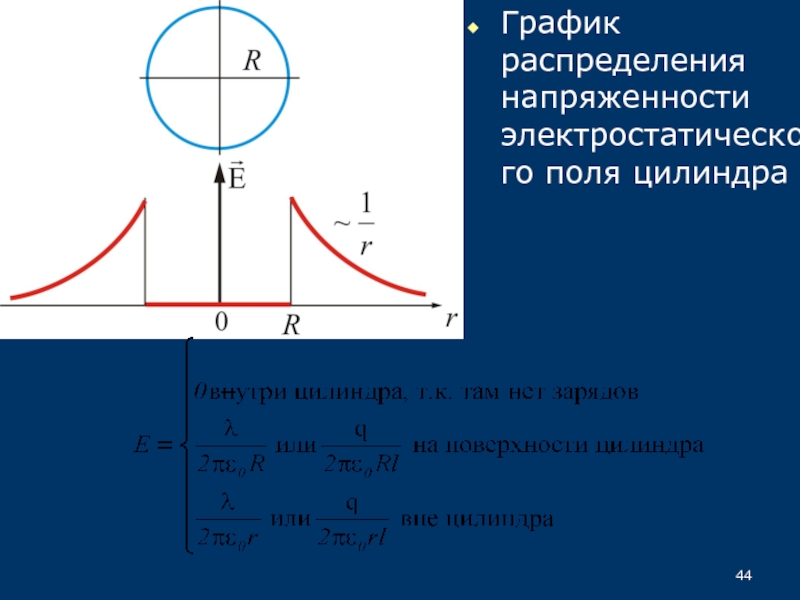
33.5.3. Поле заряженного бесконечного цилиндра (нити)
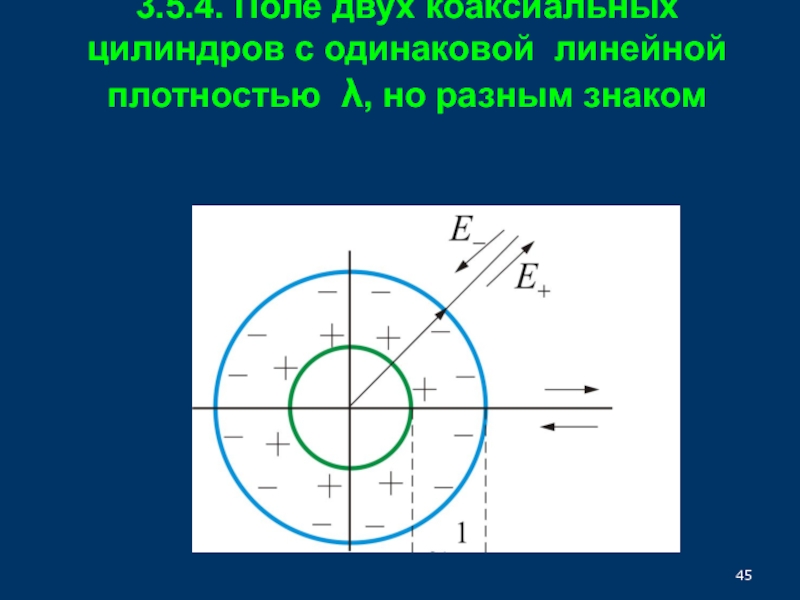
33.5.4. Поле двух коаксиальных цилиндров с одинаковой линейной плотностью заряда, но разным знаком
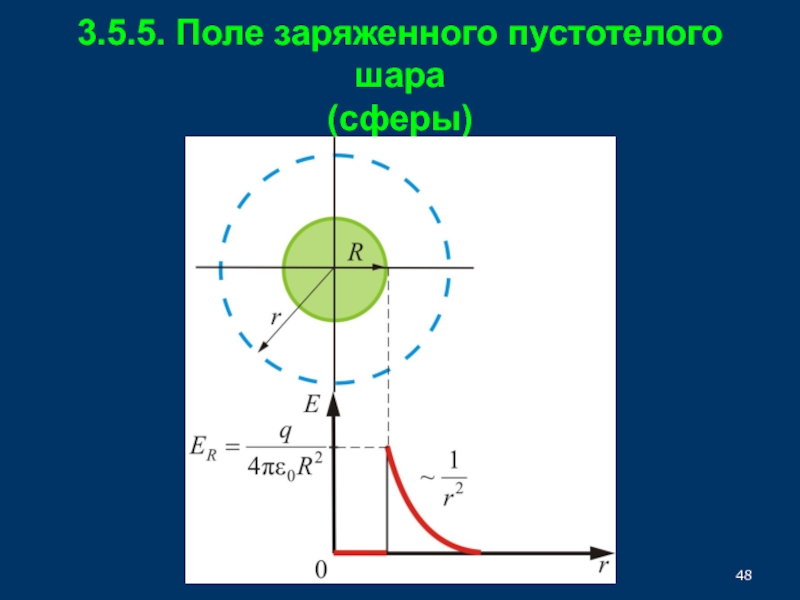
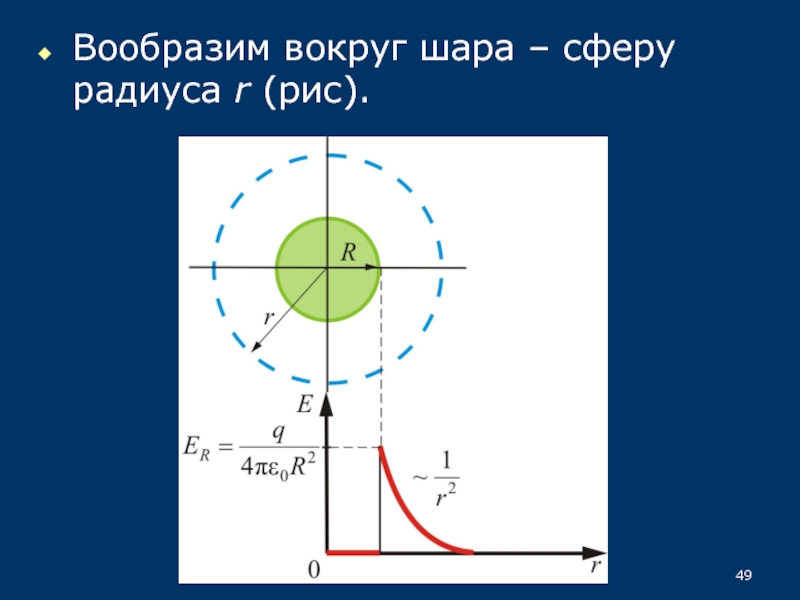
33.5.5. Поле заряженного пустотелого шара(сферы)
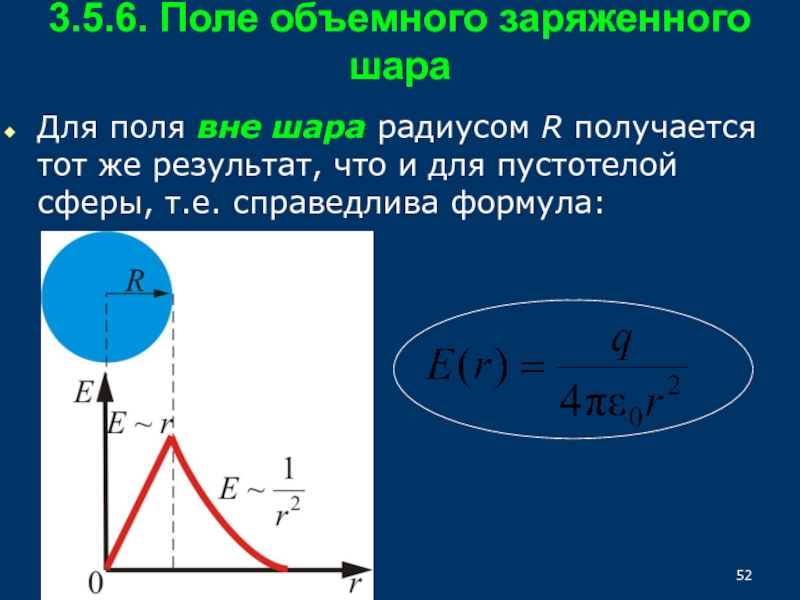
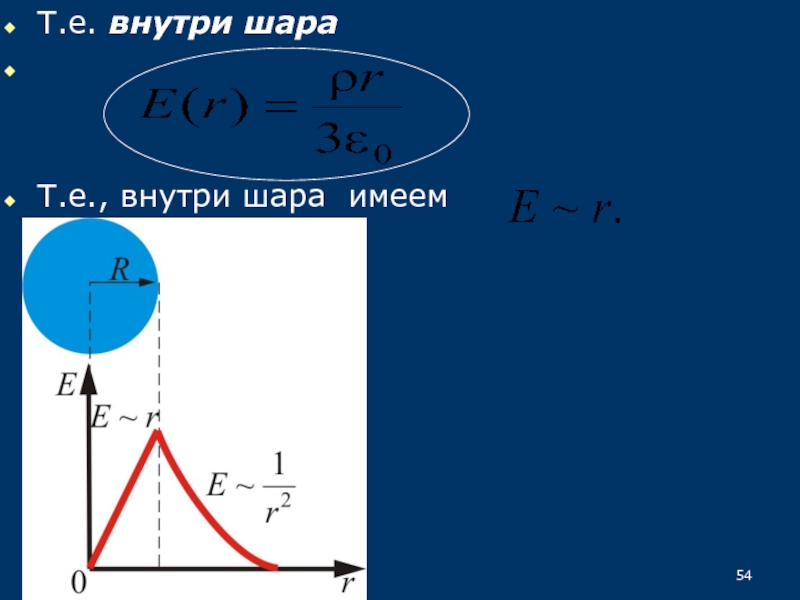
33.5.6. Поле объемного заряженного шара
3.6. Уравнения Пуассона и Лапласа.