Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема о движении центра масс
Содержание
- 1. Теорема о движении центра масс
- 2. ВведениеТеорема о движении центра масс Законы
- 3. На предыдущей лекции- Определили понятие механической системы
- 4. Изучить теоремы о движении центра масс и об изменении количества движения Цель лекции
- 5. 1 – центр масс системы 2
- 6. Напомним: Движение механической системы мы будем изучать по
- 7. ДУ движения механической системыВозьмем в качестве механической
- 8. (3)после двойного дифференцирования?Произведение массы системы на ускорение
- 9. Аналогия со 2-м законом Ньютона для точки:Центр
- 10. Из теоремы о движении центра масс можно
- 11. 2. Пусть сумма проекций внешних сил на
- 12. Движение человека. Механическая система: человек и Земля.
- 13. 4. Почему нельзя поднять самого себя за
- 14. - масса вала- масса машины- смещение центра
- 15. Центр масс всей системы вдоль оси x
- 16. - мотор не отрывается от землиРеакцию N
- 17. Количеством движения (импульсом) механическойсистемы будем называть векторную
- 18. (5)Дифференцируем это равенство по времениИз определения центра
- 19. (5)Вспомним кинематику: движение твердого тела складывается из
- 20. Для характеристики действия, оказываемого на тело силой
- 21. В частном случае:В случае приложения нескольких сил:Проекции импульса силы
- 22. Дифференцируем равенство (5) по времениСогласно теореме о
- 23. Производная по времени от количества движения механической
- 24. - внутренние силы непосредственно не могут влиять
- 25. Теорема об изменении количества движения Замечание.Импульс системы
- 26. 1. Пусть сумма внешних сил равна нулю Если
- 27. 2. Пусть проекции внешних сил
- 28. Выбрать механическую систему (удачно!)Изобразить все нужные силы
- 29. Задача 2
- 30. Задача 3
- 31. Слайд 31
- 32. Задача 5 (установившееся течение жидкости в трубе)По
- 33. Задача 6 (движение ракеты)М.С. – ракета с оставшимся в ней горючим на время t:
- 34. 1. Изучена теорема о движении центра масс
- 35. Вопросы для самоконтроля
- 36. Вопросы для самоконтроля
- 37. Тема следующей лекции Теорема об изменении момента количества движения системы
- 38. Лекция окончена!!!
- 39. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
ДИНАМИКА
Новосибирский Государственный Архитектурно-Строительный Университет (Сибстрин)
Кафедра теоретической
механики
КОЛИЧЕСТВА ДВИЖЕНИЯСлайд 2 Введение
Теорема о движении центра масс
Законы сохранения движения центра
масс
Количество движения (импульс) системы
Импульс силы
Теорема об изменении
количества движения (импульса) Рекомендации к решению задач
Примеры применения теорем
Заключение
План лекции
Слайд 3На предыдущей лекции
- Определили понятие механической системы
- Познакомились с
основными ее характеристиками: массой, центром масс, моментом инерции относительно оси
-
Определили меры движения:центр масс, количество движения (импульс), момент количества движения (момент импульса), кинетическую энергию
Слайд 5
1 – центр масс системы
2 – количество движения
(импульс) системы
3 – момент количества движения
(момент
импульса) системы4 – кинетическая энергия системы
Введение
НАПОМНИМ: МЕРЫ ДВИЖЕНИЯ
Слайд 6
Напомним:
Движение механической системы мы будем изучать по поведению ее характеристик
(мер движения) - центра масс, количества движения, момента количества движения,
кинетической энергииПоведение же этих характеристик будет определяться теоремами об их изменении со временем.
На этой лекции мы изучим первые две теоремы:
Теорему о движении центра масс
Теорему об изменении количества движения
Введение
Введение
Слайд 7
ДУ движения механической системы
Возьмем в качестве механической системы рой пчел
(1000-6000). У нас нет возможности проследить за полетом каждой из
пчел. Однако, чтобы ответить на вопрос: “куда полетели пчелы? ”, лучшей точки, чем центр масс этого роя не найти!Суммируем левые и правые части уравнений
(1)
- по свойству внутренних сил
(2)
Теорема о движении центра масс
Слайд 8
(3)
после двойного дифференцирования
?
Произведение массы системы на ускорение ее центра масс
равно сумме всех действующих на систему внешних сил
Подставляя в (2),
получим теорему о движении центра массТеорема о движении центра масс
Слайд 9
Аналогия со 2-м законом Ньютона для точки:
Центр масс системы движется
как материальная точка, масса которой равна массе всей системы и
к которой приложены все внешние силы, действующие на системуПри движении твердого тела теорема полностью определяет поступательную часть движения вместе с центром масс С. Вращательную часть движения вокруг С нам определит теорема об изменении момента количества движения (следующая лекция).
Теорема позволяет при определении движения центра масс любой механической системы исключить наперед неизвестные внутренние силы
Теорема о движении центра масс
Слайд 10
Из теоремы о движении центра масс можно получить следующие важные
следствия:
1. Пусть сумма внешних сил равна нулю
Если сумма внешних сил,
действующих на механическую систему равна нулю, то ее центр масс движется равномерно прямолинейно. В частности, если в начальный момент центр масс был в покое, то он и останется в покое.
Тогда из уравнения
следует
Законы сохранения движения центра масс
Слайд 11
2. Пусть сумма проекций внешних
сил на ось X равна
нулю
Если сумма проекций всех действующих внешних сил на ось равна
нулю, то проекция скорости центра масс на эту ось не меняетсяВ частности, если в начальный момент скорость центра масс системы вдоль оси равна нулю, то центр масс системы вдоль этой оси перемещаться не будет
Тогда
Следствие. Пара сил, приложенная к твердому телу, не может изменить движение его центра масс (она может только вызвать вращение тела вокруг центра масс).
Законы сохранения движения центра масс
Слайд 12
Движение человека. Механическая система: человек и Земля. Сила сцепления между
подошвами обуви и Землей – внутренняя. Поэтому центр масс системы
“человек + Земля” должен остаться в покое.2. Откат орудия при выстреле. Механическая система: орудие и снаряд. Если снаряд вылетает вперед, то орудие, если оно не закреплено, откатывается назад.
3. Вращающиеся тела со смещенным центром масс. Вращающиеся части конструкций обычно “центруют” так, чтобы, в частности, их центры масс находились на оси вращения.
Примеры
Слайд 13
4. Почему нельзя поднять самого себя за волосы?
5. А почему
другой человек сможет?
6. Прыжок с вышки в бассейн “солдатиком”
7. То
же самое, только с гирей в рукахПримеры (продолжение)
Слайд 14
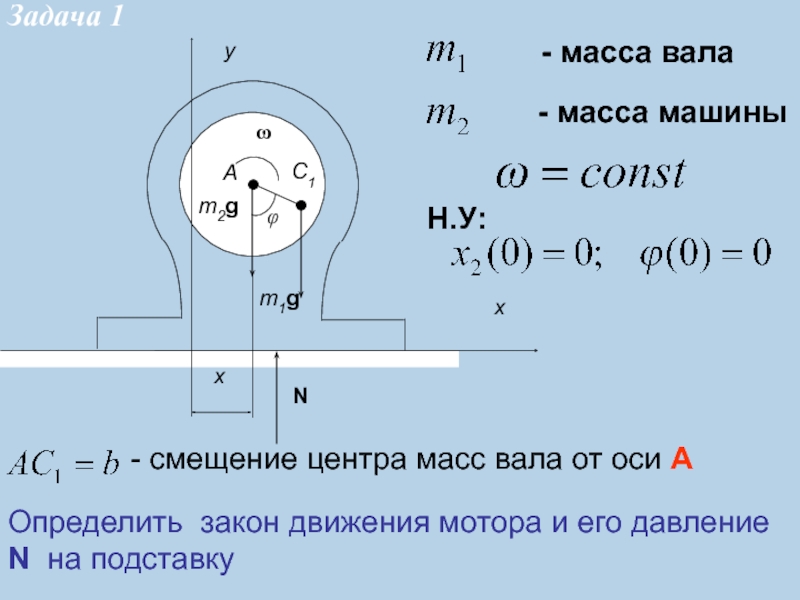
- масса вала
- масса машины
- смещение центра масс вала от
оси А
Определить закон движения мотора и его давление N на
подставкуН.У:
Задача 1
Слайд 15
Центр масс всей системы вдоль оси x двигаться не будет:
Механическая
система: мотор + вал
Внешние силы:
- теорема
Задача (продолжение)
Слайд 16
- мотор не отрывается от земли
Реакцию N найдем из второго
уравнения
Следовательно, мотор будет совершать гармонические колебания
- мотор подпрыгивает
статическое + динамическое
давлениеЗадача (продолжение)
- мотор подпрыгивает
Понятно, почему вибрируют стиральные машины!
Слайд 17
Количеством движения (импульсом) механической
системы будем называть векторную величину, равную сумме
количеств движения всех ее точек
Единицей измерения в СИ является
1 кг*м/с- количество движения k-ой точки
(4)
Количество движения (импульс) системы
Слайд 18
(5)
Дифференцируем это равенство по времени
Из определения центра масс
Отсюда находим
Количество движения
системы равно произведению массы системы на скорость ее центра масс.
Другими
словами, количество движения всей системыравно количеству движения ее центра масс, если в ней сосредоточить всю массу системы
Количество движения (импульс) системы
Слайд 19
(5)
Вспомним кинематику: движение твердого тела складывается из поступательного (вместе с
С) и вращательного (вокруг С).
Из (5) следует, что при
вращательном движении вокруг C количество движения равно нулю.Следовательно, количество движения системы характеризует ее поступательное движение вместе с центом масс
(6)
Проекции количества движения системы
Слайд 20
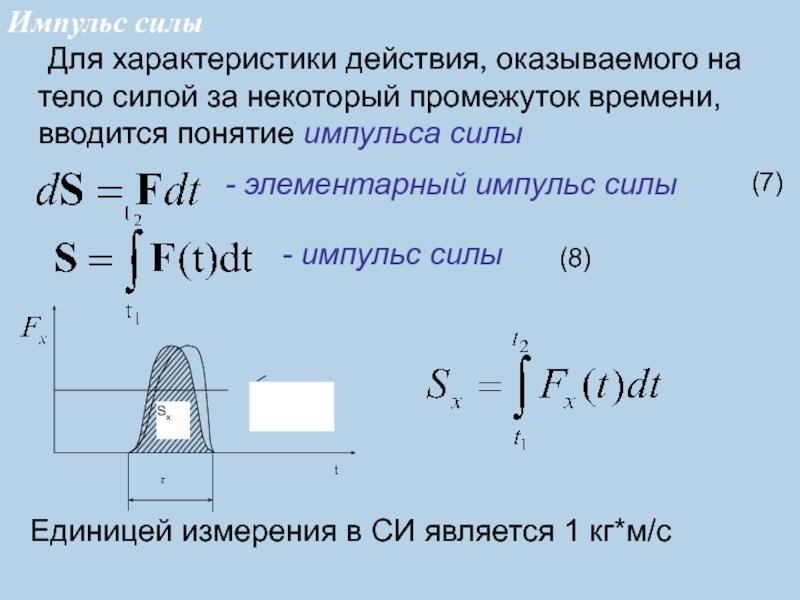
Для характеристики действия, оказываемого на тело силой за некоторый промежуток
времени, вводится понятие импульса силы
(7)
- элементарный импульс силы
- импульс силы
(8)
Единицей измерения в СИ является 1 кг*м/с
Импульс силы
Слайд 22
Дифференцируем равенство (5) по времени
Согласно теореме о движении центра масс
(5)
следовательно
получим
(9)
Теорема об изменении количества движения (импульса) системы
Слайд 23
Производная по времени от количества движения механической системы равна главному
вектору действующих на нее внешних сил
Теорема чаще используется в интегральной
форме - дифференциальная форма
(9)
(10)
Изменение импульса за промежуток времени равно сумме импульсов действующих на нее внешних сил за тот же промежуток
Теорема об изменении количества движения (импульса) системы
Слайд 24
- внутренние силы непосредственно не могут влиять на изменение импульса
системы
- механическую систему выбирают так, чтобы наперед неизвестные силы сделать
внутренними(11)
Теорема об изменении количества движения в проекциях
Слайд 25
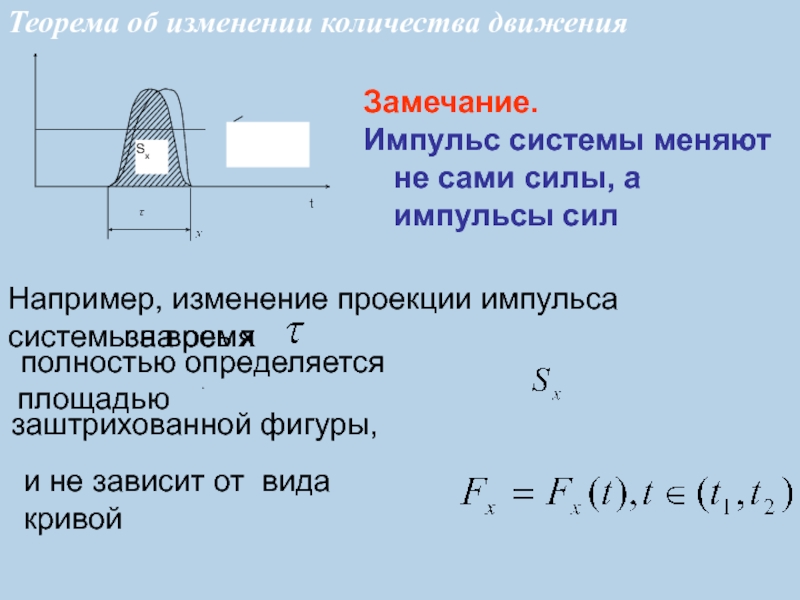
Теорема об изменении количества движения
Замечание.
Импульс системы меняют не сами
силы, а импульсы сил
Например, изменение проекции импульса системы на ось
x за время
полностью определяется площадью
заштрихованной фигуры,
.
и не зависит от вида кривой
Слайд 26
1. Пусть сумма внешних сил равна нулю
Если сумма внешних сил,
действующих на механическую систему равна нулю, то вектор количества движения
сохраняется во все время движения Тогда из уравнения
следует
Если за некоторый промежуток времени сумма импульсов внешних сил равна нулю
(12)
Закон сохранения количества движения
Слайд 27
2. Пусть проекции внешних сил
на X равны
нулю
Если сумма проекций всех действующих на систему внешних сил на
ось равна нулю, то проекция количества движения на эту ось сохраняется во времени Тогда из уравнения
следует
Если равна нулю проекция суммы импульсов внешних сил за промежуток времени
Закон сохранения количества движения
Слайд 28Выбрать механическую систему (удачно!)
Изобразить все нужные силы (активные и реакции
связей)
Записать одну из общих теорем динамики(или несколько)
Проинтегрировать полученную систему уравнений.
Постоянные интегрирования определяются при этом из дополнительных (начальных) условий задачиОпределить искомые величины
Рекомендации к решению задач на применение общих теорем динамики
Слайд 29Задача 2
Пуля весом P, летящая горизонтально со скоростью u,
попадает в тележку с песком веса Q и застревает в ней. С какой скоростью будет двигаться тележка? Трением и сопротивлением воздуха пренебречь.Решение. 1. Механическая система: пуля + тележка
2. Внешние силы, действующие на систему P,Q,N,R.
3. Запишем теорему об изменении количества движения системы в проекции на горизонтальную ось x.
Слайд 30Задача 3
Однородный стержень AB длиной 2L, опирающийся нижним концом A на
гладкую горизонтальную плоскость, начинает падать из состояния покоя, образуя при t=0 угол с плоскостью. Определить траекторию верхнего конца B стержня.Решение. 1. М.с. – стержень AB; 2. Внешние силы N, mg;
3. Теор. о дв. центра масс:
Траектория т. B – эллипс;
Слайд 31
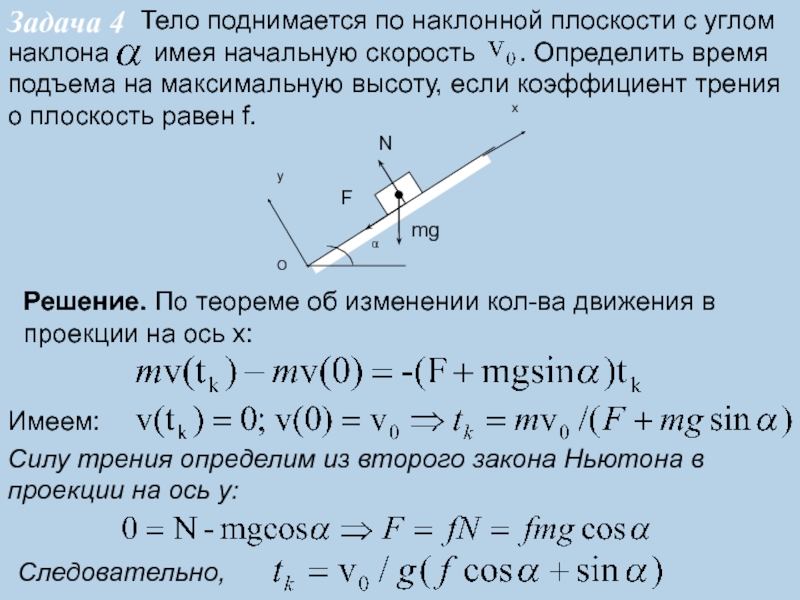
Тело
поднимается по наклонной плоскости с углом наклона имея
начальную скорость . Определить время подъема на максимальную высоту, если коэффициент трения о плоскость равен f.Задача 4
Решение. По теореме об изменении кол-ва движения в проекции на ось x:
Имеем:
Силу трения определим из второго закона Ньютона в проекции на ось y:
Следовательно,
Слайд 32
Задача 5 (установившееся течение жидкости в трубе)
По теореме об изменении
импульса имеем:
Возьмем в качестве М.С. – объем жидкости
abcd (в момент t). В момент t+ он займет положение Слайд 34
1. Изучена теорема о движении центра масс
и ее частные
случаи - законы сохранения движения центра масс
2. Определено понятие импульса
силы 3. Изучена теорема об изменении количества движения (импульса) и ее частные случаи – законы сохранения импульса
4. Даны рекомендации к решению задач на применение общих теорем динамики
5. Рассмотрены примеры решения задач с использованием этих рекомендаций
Заключение
Слайд 35
Вопросы для самоконтроля
1. Каким уравнением
описывается движение центра масс?
2. Почему внутренние силы, действующие на систему,
не влияют на движение ее центра масс?3. В каком случае центр масс системы остается в покое?
4. Когда центр масс системы движется в направлении некоторой оси равномерно?
5. Почему человек не может сам себя поднять за волосы? А почему может присесть и какое при этом его давление на пол?
6. Какое действие на твердое тело оказывает приложенная к нему пара сил?
7. Как определяется импульс силы за конечный промежуток времени?
8. Как определяется количество движения системы?
9. Сформулируйте теорему об изменении количества движения системы в дифференциальной и интегральной формах.
Слайд 36
Вопросы для самоконтроля
10. При каких
условиях количество движения системы не изменяется?
11. При каких условиях не
меняется проекция количества движения на данную ось?12. Можно ли за счет внутренних усилий изменить количество движения системы?
13. Почему происходит откат орудия при выстреле?
14. Перечислите основные этапы решения задач на применение теоремы о движении центра масс или теоремы об изменении импульса системы.
15. Почему решение задач следует начинать с выбора механической системы?
16. В каких системах координат справедливы теоремы о движении центра масс и об изменении импульса системы?