Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема об отрезках пересекающихся хорд
Содержание
- 1. Теорема об отрезках пересекающихся хорд
- 2. ПРОВЕРЯЕМ ДОМАШНЕЕ ЗАДАНИЕ
- 3. Слайд 3
- 4. Слайд 4
- 5. ЗАДАЧИ НА ГОТОВЫХ ЧЕРТЕЖАХ
- 6. О ВА С8001. Найти угол АВС ПРОВЕРИМ400
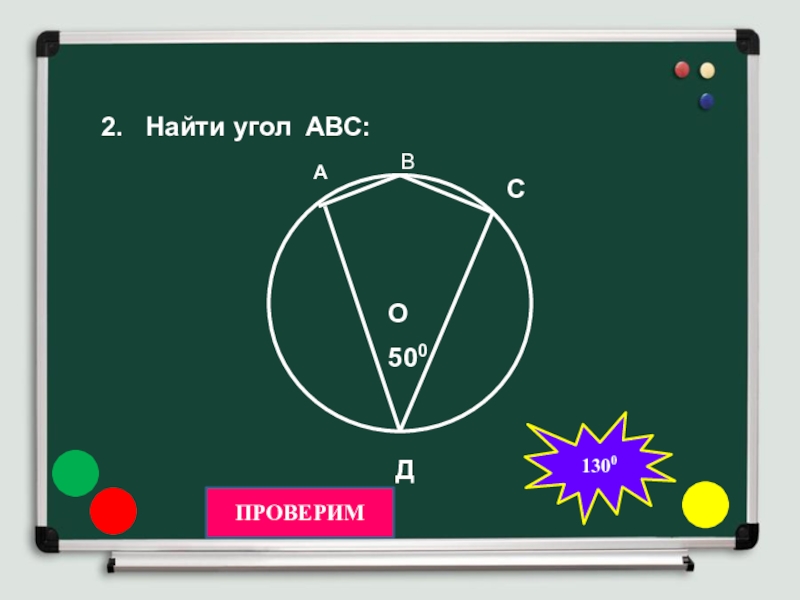
- 7. 2. Найти угол АВС: ОАВ СД 500ПРОВЕРИМ1300
- 8. 3. Найти угол А и угол СО 370 А С ВПРОВЕРИМ530900
- 9. 4. Найти угол АОД и угол АСД : О 400 В А Д СПРОВЕРИМ800400
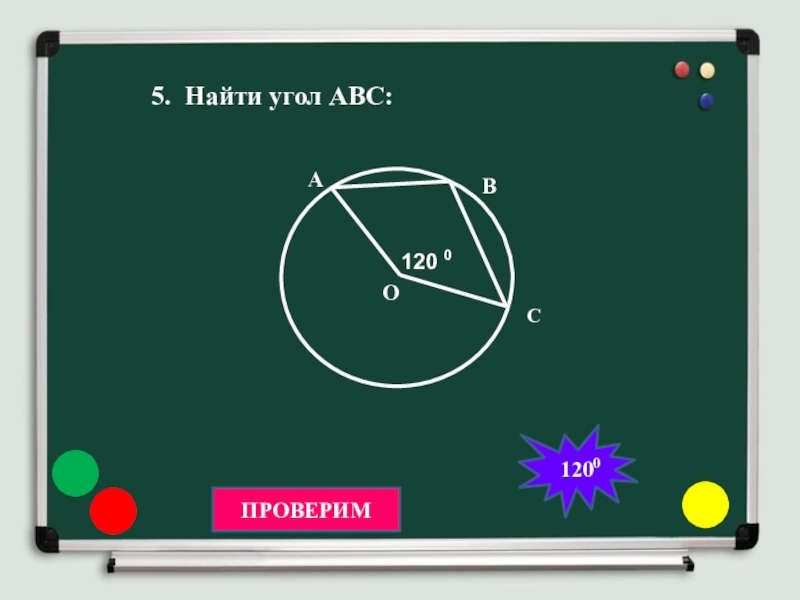
- 10. 5. Найти угол АВС: О 120 0 А ВСПРОВЕРИМ 1200
- 11. Упражнения для глаз
- 12. Слайд 12
- 13. Задача: Найти АЕ , если ВЕ=4
- 14. План-конспект доказательства теоремы.
- 15. Задача : Докажите , что если две
- 16. Задача №660
- 17. Задача №667:
- 18. Задача №670 .
- 19. Домашнее задание:П.71 , стр.173, вопрос 14,№№ 666(б), 671(б), 660(б)
- 20. Скачать презентанцию
Слайды и текст этой презентации
Слайд 13Задача: Найти АЕ , если ВЕ=4 см, DE =
6 см ,СЕ=2см.
Доказать , треугольник АЕС подобен треуголь нику DBE.
А Е
D
C
В
Решение.
АЕС подобен DEB т.к.
угол AED и угол ABD вписанные и
опираются на одну дугу. Угол AEC
И угол DEB равны как вертикальные
( первый признак подобия), отсюда
Стороны треугольников пропорциональны
AE : ED = BE: CE, AE : 6= 4: 2
отсюда АЕ = 6 * 4 :2 =12см.
Слайд 14План-конспект доказательства теоремы.
а
а) треугольники АСЕ и DBE подобны т. к угол А равен углу D как вписанные углы ,опирающиеся на дугу ВС , углы AEC и DEB равны как вертикальные.
в) AE:DE= CE:BE, отсюда AE*BE= CE*DE.
Вопросы для обсуждения.
- Что вы можете сказать об углах CAB и CDB. Об углах AEC и DEB.
- Какими являются треугольники ACE и DBE. Чему равно отношение их сторон,
являющихся отрезками хорд касательных.
-Какое равенство можно записать из равенства двух отношений , используя основное свойство пропорции.
.
Слайд 15Задача : Докажите , что если две хорды AB и
CD окружности пересекаются в точке Е , то АЕ *
ВЕ =СЕ *DE.А
D
C
B
1
2
E
Доказательство :
Рассмотрим треугольники ADE и СВЕ. на Углы 1 и 2 равны, т. к они вписанные и опираются на одну и ту же дугу BD . Углы 3 и 4 равны как вертикальные. Следовательно треугольники подобны по первому признаку.
Отсюда AE : CE =DE: BE или
AE *BE=CE*DE.
Слайд 16 Задача №660
Дано:
АС,АЕ – секущие
угол АСЕ равен 320
угол АОЕ равен 1000
Найти дугу ВD
С
В
А
D
Е
О
Решение.
Угол АВЕ- вписанный равен половине дуги на которую он опирается, т.е. половине дуги АЕ- 500
Углы ЕВС и АВЕ смежные, значит
угол ВЕD = 1800 (1300 + 320 ) =180,
Отсюда дуга BD= 2 * BED ,BD=360
Слайд 17Задача №667:
Треугольник ОВВ1
равнобедренныйОС ВВ1 является высотой и
медианой в треугольнике ОВВ1 ,то есть
ВС=В1С . АА1 и ВВ1- хорды,
пересекающиеся в точке С, тогда
А1С*АС = В1 С * ВС
Т.к В1С= ВС, то ВС2= 8*4 =32,
ВС= 4 √2 см, а ВВ1 =8√ 2
Ответ: 8√ 2
.
О
А1
А
В
В1
С
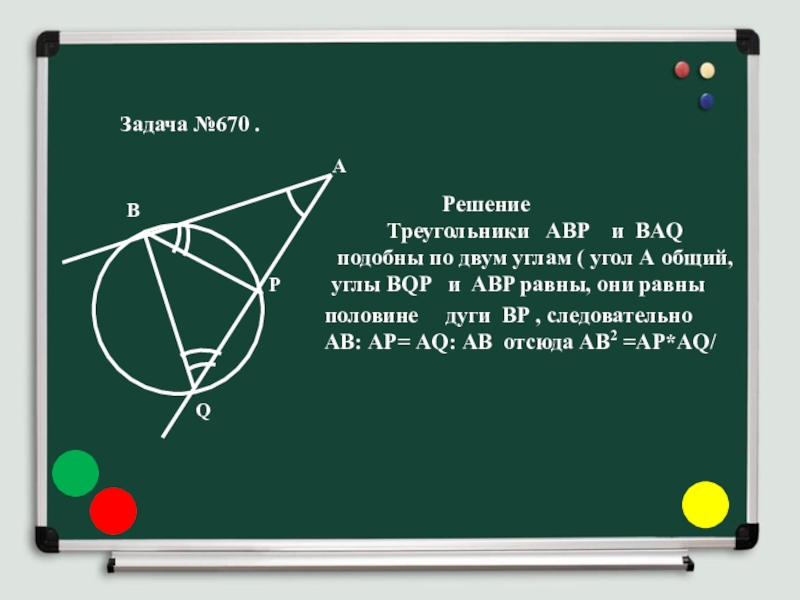
Слайд 18Задача №670 .
Решение
Треугольники ABP и BAQ
подобны по двум углам ( угол А общий,
углы BQP и ABP равны, они равны
В
А
Р
Q
половине дуги ВР , следовательно
АВ: АР= AQ: АВ отсюда АВ2 =AP*AQ/