Теоретические основы компьютера

другую и обратно
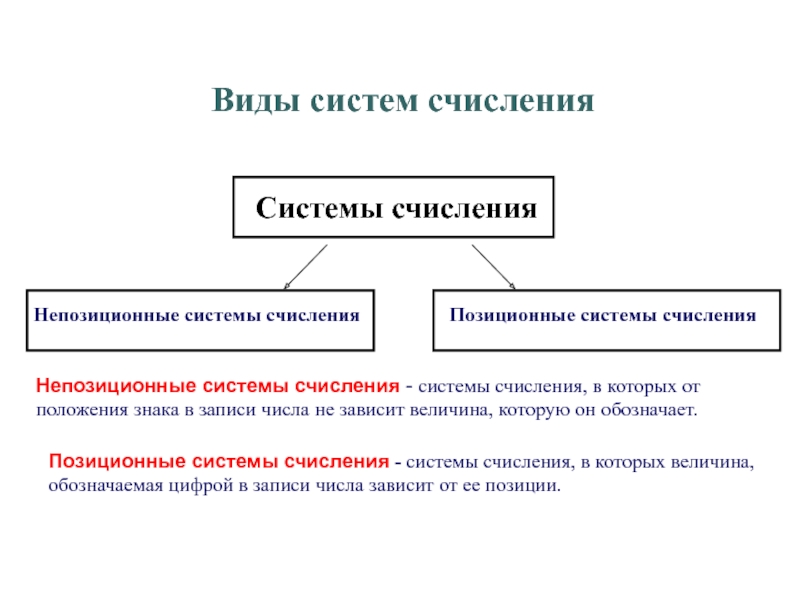
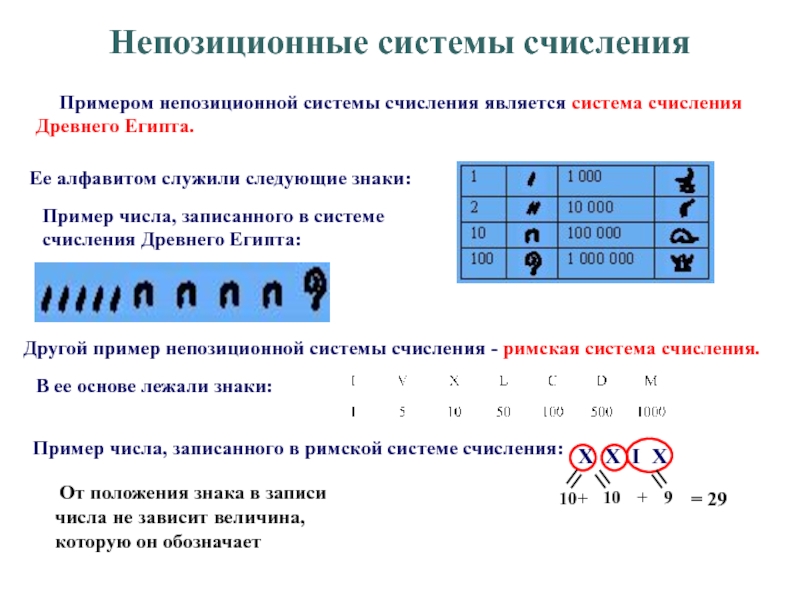
Системы счисления. Виды систем счисления.
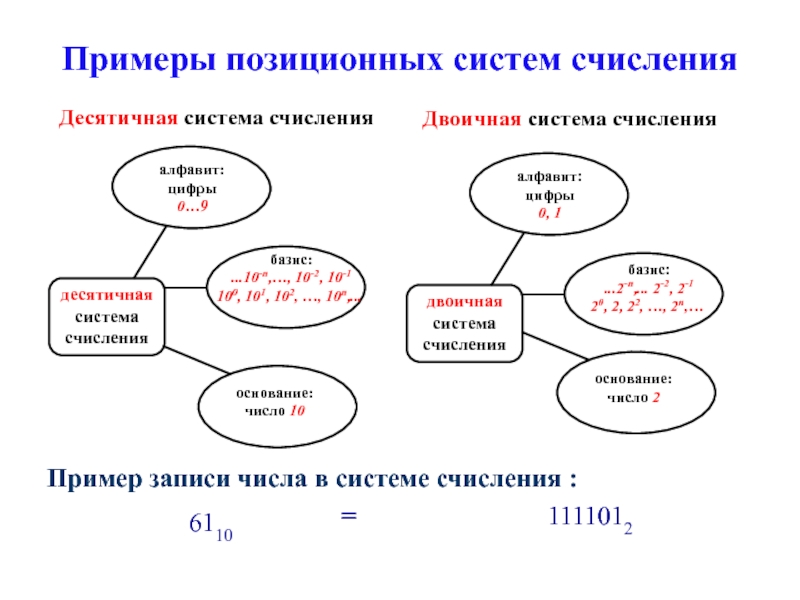
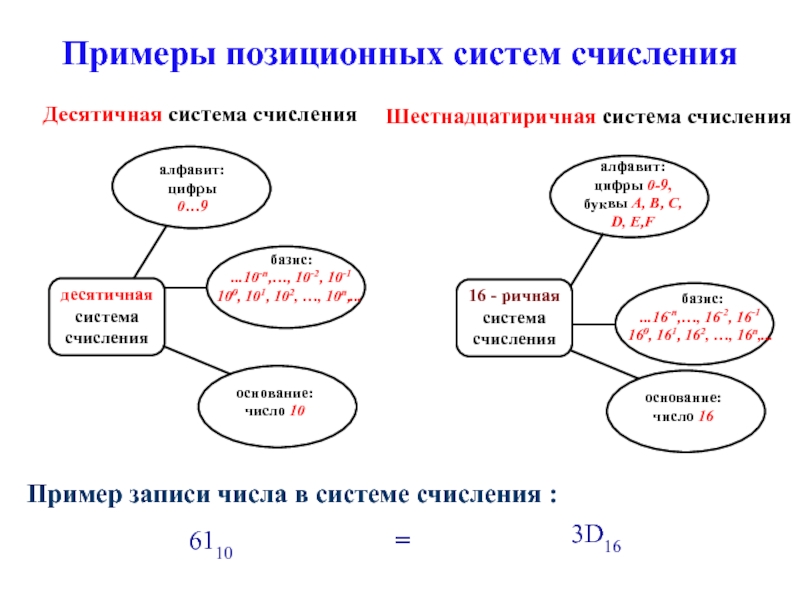
Перевод десятичных чисел

из десятичной системы счисления в любую другую и обратно.
Перевод целых чисел из десятичной системы счисления с помощью приложения Калькулятор в двоичную, восьмеричную, шестнадцатеричную системы счисления.
Перевод целых чисел из десятичной системы счисления с помощью приложения Excel в двоичную, восьмеричную, шестнадцатеричную системы счисления, используя общий метод перевода.

- это символ, используемый в записи числа.
12
Алфавит системы счисления -

это множество всех символов (знаков), используемых для записи чисел в данной системе счисления.

двенадцать

ХII

- значение числа остается неизменным

0, 1, 2, 3, 4, 5, 6, 7, 8, 9 - алфавит десятичной позиционной системы счисления

I, V, X, L, C, D, M - алфавит римской непозиционной системы счисления

от положения знака в записи числа не зависит величина, которую

он обозначает.

Позиционные системы счисления - системы счисления, в которых величина, обозначаемая цифрой в записи числа зависит от ее позиции.

Египта.
Ее алфавитом служили следующие знаки:
Пример числа, записанного в системе счисления

Древнего Египта:

Другой пример непозиционной системы счисления - римская система счисления.

В ее основе лежали знаки:

Пример числа, записанного в римской системе счисления:

X X I Х

От положения знака в записи числа не зависит величина, которую он обозначает

= 29

103 + 2 ·102 + 5 · 101 + 5

· 100

Число в позиционной системе счисления

Привычная нам десятичная система является позиционной системой счисления:

Цифры 5, находящиеся на разных позициях, имеют различные количественные значения .

Базис позиционной системы счисления - последовательность чисел, каждое из которых определяет количественный эквивалент (вес) символа в зависимости от его места в записи числа.

Основание позиционной системы счисления - целое число, которое возводится в степень.

101, 102, 103, 104, … , 10n, … - базис десятичной позиционной системы счисления.

10 - основание десятичной позиционной системы счисления.

155255 =

bп + … + a0 · b0 + a-1 ·

b-1 + ...

2534,65 =

1 ·105 + 5 ·104 + 5 ·103 + 2 ·102 + 5 ·101 + 5 ·100

2 ·103 + 5 ·102 + 3 ·101 + 4 ·100 + 6 ·10-1 + 5 ·10-2

записи числа в системе счисления :

счисления :
Примеры позиционных систем счисления

на 2)
Нахождение дробной части числа (умножение на 2)
Целая часть :

1 0 0 1 0 0 1 1 0 1 1 1

Дробная часть : 0 1 1 0 1 0 0

2359,407 = 1 0 0 1 0 0 1 1 0 1 1 1, 0 1 1 0 1 0 02

другую
Режим работы в двоичной системе счисления 1111012
Режим работы в

восьмеричной системе счисления 758

Режим работы в десятичной системе счисления 6110

Режим работы в шестнадцатиричной системе счисления 3D16

записи двоичных чисел используются две цифры, т.е. в каждом разряде

числа возможны два варианта записи.
Каждый разряд двоичного числа содержит 1 бит.

Алгоритмы, описанные ниже, могут применяться при переводе чисел между системами счисления, основания которых являются степенями числа 2.

Такие алгоритмы могут применяться для перевода чисел между двоичной, восьмеричной и шестнадцатеричной системами счисления.

Для записи восьмеричных чисел используются восемь цифр, т.е. в каждом разряде числа возможны восемь вариантов записи.
Каждый разряд восьмеричного числа содержит 3 бита.

Для записи шестнадцатеричных чисел используются шестнадцать цифр, т.е. в каждом разряде числа возможны шестнадцать вариантов записи.
Каждый разряд шестнадцатеричного числа содержит 4 бита.

слева направо на триады (если в последней правой группе окажется

меньше, чем три разряда, то необходимо её дополнить справа нулями)
Преобразовать каждую триаду в восьмеричную цифру

Переведём таким образом двоичное число 0,1101012 в восьмеричное:

Получаем 0,1101012 = 0,658

группы по четыре цифры (тетрады), справа налево (если в последней

левой группе окажется меньше, чем четыре разряда, то необходимо её дополнить слева нулями)
Преобразовать каждую группу в шестнадцатеричную цифру

Переведём таким образом двоичное число 1010012 в шестнадцатеричное:

Получаем 1010012 = 2916

тетрады, слева направо (если в последней правой группе окажется меньше,

чем четыре разряда, то необходимо её дополнить справа нулями)
Преобразовать каждую группу в шестнадцатеричную цифру, воспользовавшись для этого предварительно составленной таблицей соответствия двоичных тетрад и шестнадцатеричных цифр

Переведём таким образом дробное двоичное число 0,1101012 в шестнадцатеричную систему счисления:

Получаем 0,1101012 = 0,D416

из восьмеричной системы в двоичную каждую цифру числа надо преобразовать

в триаду

для перевода из шестнадцатеричной системы в двоичную каждую цифру числа надо преобразовать в тетраду

Переведём дробное восьмеричное число 0,478 в двоичную систему счисления:

Получаем 0,478 = 0,1001112

Переведём целое шестнадцатеричное число АВ1616 в двоичную систему счисления:

Получаем АВ1616 = 101010112

группы по три цифры, справа налево (если в последней левой

группе окажется меньше, чем три разряда, то необходимо её дополнить слева нулями)
Преобразовать каждую группу в восьмеричную цифру

Переведём таким образом двоичное число 1010012 в восьмеричное:

101

518

Для упрощения перевода можно заранее подготовить таблицу преобразования двоичных триад (групп по три цифры) в восьмеричные цифры.

001

2

=

другую
ПРИМЕР
Перевести число 2359 из десятичной системы счисления в шестнадцатиричную при

помощи калькулятора

Выбираем режим работы в той системе, в которой дано число ( десятичная система);

Набираем число, с которым хотим работать (2359);

Переключаемся в режим работы системы счисления, в которой требуется получить ответ (шестнадцатиричная система) и получаем результат.