Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория автоматического управления Лекция 8. Устойчивость систем
Содержание
- 1. Теория автоматического управления Лекция 8. Устойчивость систем
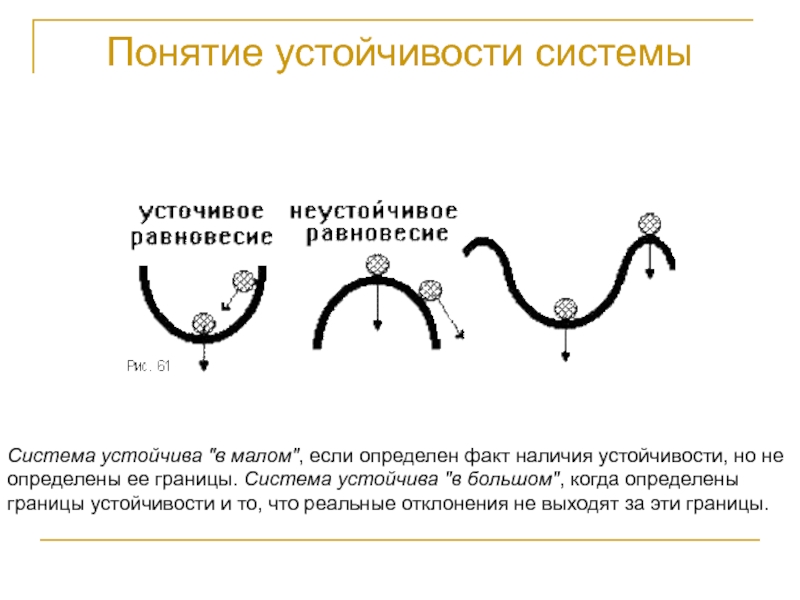
- 2. Понятие устойчивости системыСистема устойчива "в малом", если
- 3. Понятие устойчивости системыy(t) = yвын(t) + yсв(t).aoy(n)
- 4. Понятие устойчивости системы
- 5. Алгебраические критерии устойчивости D(p) = aopn +
- 6. Критерий Рауса Раус предложил критерий устойчивости САУ
- 7. Критерий Гурвица Из коэффициентов характеристического уравнения строится
- 8. Критерий ГурвицаКритерий Гурвица применяют при n 4.
- 9. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Понятие устойчивости системы
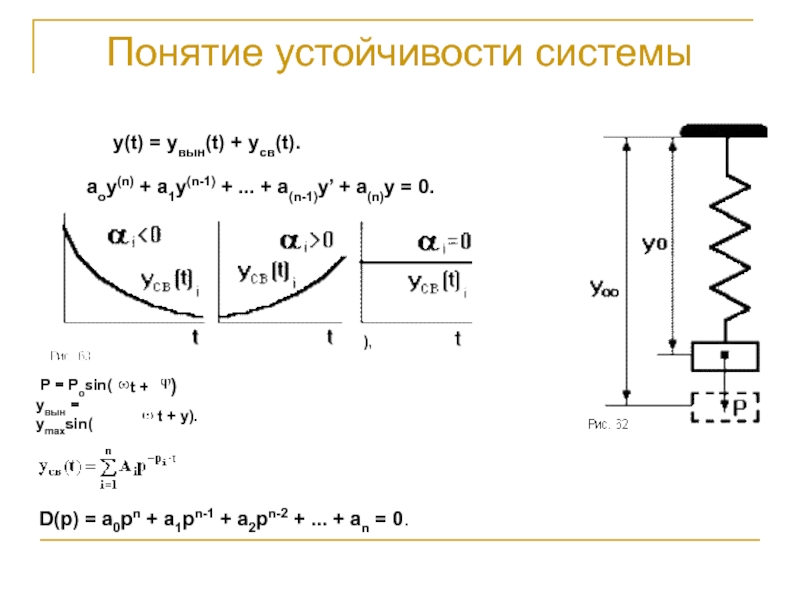
y(t) = yвын(t) + yсв(t).
aoy(n) + a1y(n-1) +
... + a(n-1)y’ + a(n)y = 0.
P = Posin(
t +
),
)
yвын = ymaxsin(
t + y).
D(p) = a0pn + a1pn-1 + a2pn-2 + ... + an = 0.
Слайд 5Алгебраические критерии устойчивости
D(p) = aopn + a1pn-1 + a2pn-2
+ ... + an = ao(p-p1)(p-p2)...(p-pn) = 0,
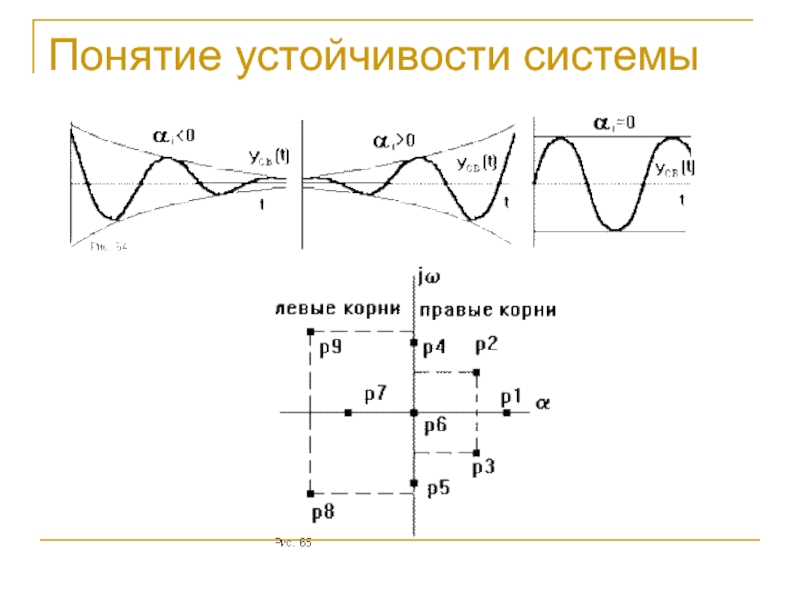
где p1,
p2, ..., pn - корни этого уравнения. Если система устойчива, значит все корни левые, то есть вещественные части всех корней отрицательны, что можно записать как ai = -|ai| < 0. Необходимым условием устойчивости САУ является положительность всех коэффициентов характеристического уравнения: a0 > 0, a1 > 0, ... , an > 0.
Эти условия являются необходимыми, но не достаточными условиями.
Слайд 6Критерий Рауса
Раус предложил критерий устойчивости САУ в виде алгоритма,
по которому заполняется специальная таблица с использованием коэффициентов характеристического уравнения:
1)
в первой строке записываются коэффициенты уравнения с четными индексами в порядке их возрастания;2) во второй строке - с нечетными;
3) остальные элементы таблицы определяется по формуле с учетом номера столбца и номера строки.
4) Число строк таблицы Рауса на единицу больше порядка характеристического уравнения.
Критерий Рауса: для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса были положительными. Если это не выполняется, то система неустойчива, а количество правых корней равно числу перемен знака в первом столбце. Достоинство - критерий прост в использовании независимо от порядка характеристического уравнения. Он удобен для использования на ЭВМ. Его недостаток - малая наглядность, трудно судить о степени устойчивости системы, на сколько далеко отстоит она от границы устойчивости.
Слайд 7Критерий Гурвица
Из коэффициентов характеристического уравнения строится определитель Гурвица
по
алгоритму:
1) по главной диагонали слева направо выставляются все коэффициенты характеристического
уравнения от a1 до an;2) от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы убывали сверху вниз;
3) на место коэффициентов с индексами меньше нуля или больше n ставятся нули.
Критерий Гурвица: для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы все n диагональных миноров определителя Гурвица были положительны. Эти миноры называются определителями Гурвица.
Слайд 8Критерий Гурвица
Критерий Гурвица применяют при n
4.
При больших порядках
возрастает число определителей и процесс становится трудоемким. Имеется ряд модификаций
данного критерия, расширяющие его возможности.Недостаток критерия Гурвица - малая наглядность. Достоинство - удобен для реализации на ЭВМ. Его часто используют для определения влияния одного из параметров САУ на ее устойчивость.