Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория графов от Эйлера до социальных сетей
Содержание
- 1. Теория графов от Эйлера до социальных сетей
- 2. «Отец» теории графов Леонард ЭйлерЗадача о
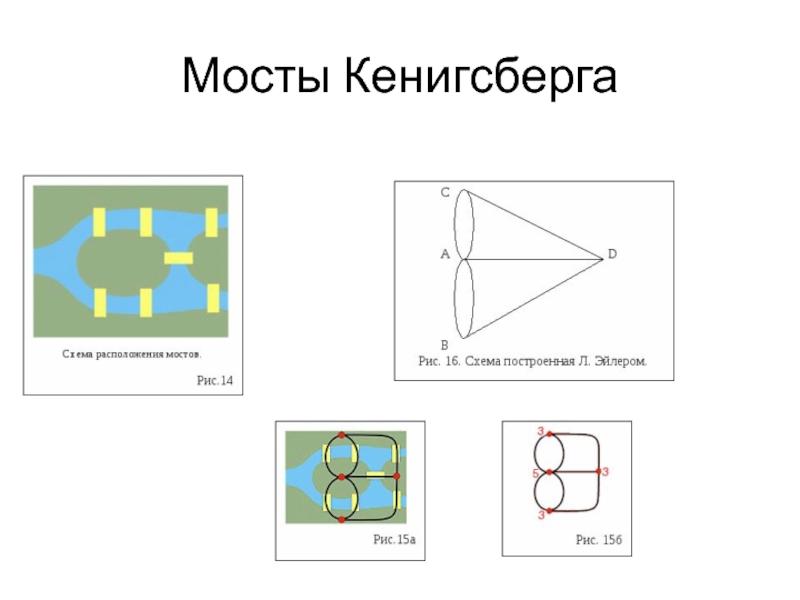
- 3. Мосты Кенигсберга
- 4. Если дана геометрическая фигура, как начертить ее
- 5. Прикладные задачи1847 годФизик Густав Роберт КирхгофТеория графов для исследования электрических цепейМножество фундаментальных циклов в графе
- 6. Прикладные задачи1857 годМатематик Артур КэлиЗадачи органической химии
- 7. Перечислить число предельных углеводородов с данным числом
- 8. Головоломки1859 годСэр Уи́льям Ро́уэн Га́мильтонГоловоломка «Вокруг света»
- 9. Головоломка «Вокруг света»Додекаэдр, каждому из 20 вершин
- 10. Слайд 10
- 11. Задача коммивояжера (англ. Travelling salesman problem, TSP) — задача,
- 12. Задача о домиках и колодцах Три
- 13. Полный двудольный граф К3,3Доказано, что данный граф
- 14. Задача о раскраске карт или гипотеза о
- 15. Задача о раскраске карт или гипотеза о
- 16. 1975 г. известный популяризатор науки и многолетний ведущий
- 17. 1976 г. два математика из Иллинойского университета, Вольфганг
- 18. ПримерыВершины – города, ребра - дороги между
- 19. Теория графов в игре престоловhttps://habrahabr.ru/post/302936/Граф социальной активностиВершинам
- 20. Слайд 20
- 21. Общие сведения о графеГраф неориентированный. Вершин (персонажей):
- 22. Алгоритмы на графеПодсчет степеней вершин – самые
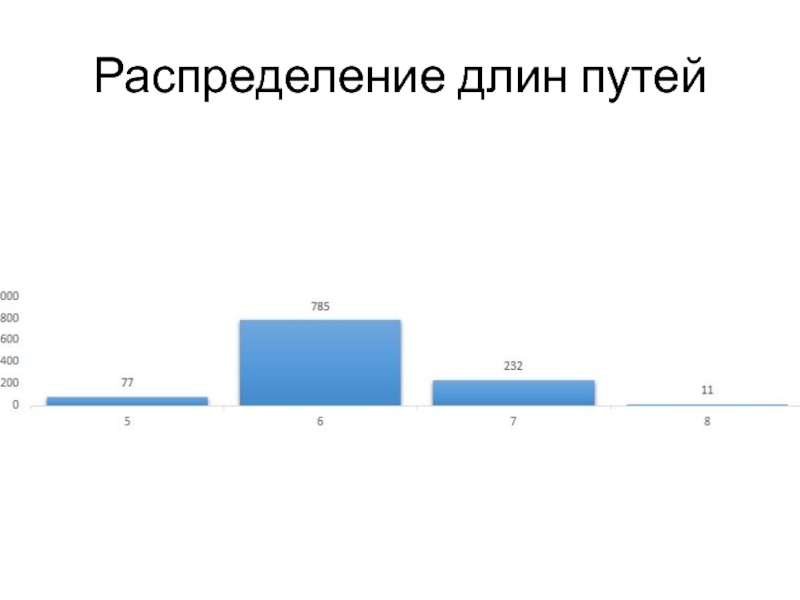
- 23. Распределение длин путей
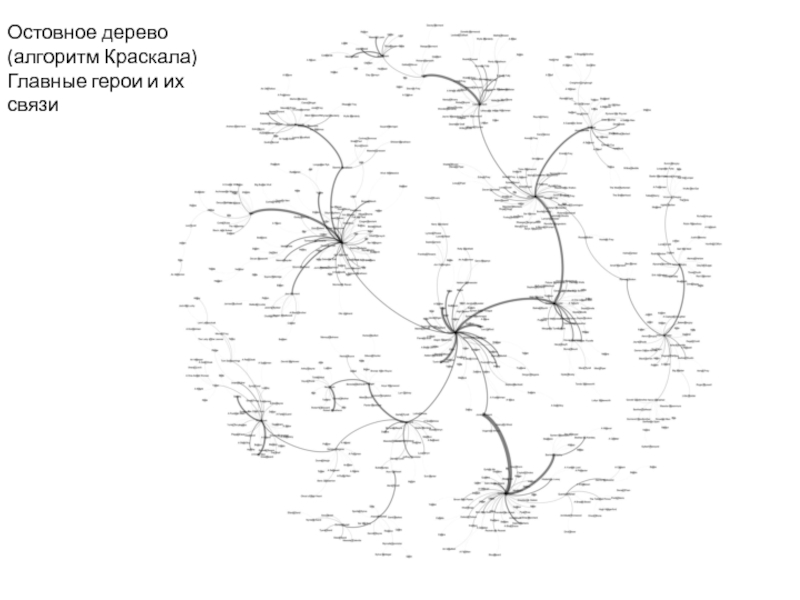
- 24. Остовное дерево(алгоритм Краскала)Главные герои и их связи
- 25. Математическая модель интернета – веб-граф (А.Райгородский)http://elementy.ru/nauchno-populyarnaya_biblioteka/431792/Matematicheskie_modeli_interneta
- 26. Свойства веб-графаДиаметр веб-графа равен 6 (закон шести
- 27. Алгоритм PageRankPageRank был представлен и опубликован Сергеем Брином
- 28. Алгоритм PageRank и футбольные команды https://geektimes.ru/post/247244/
- 29. Теория графов и реконструкция генома http://kvant.mccme.ru/pdf/2014/2014-03.pdfГраф де
- 30. Слайд 30
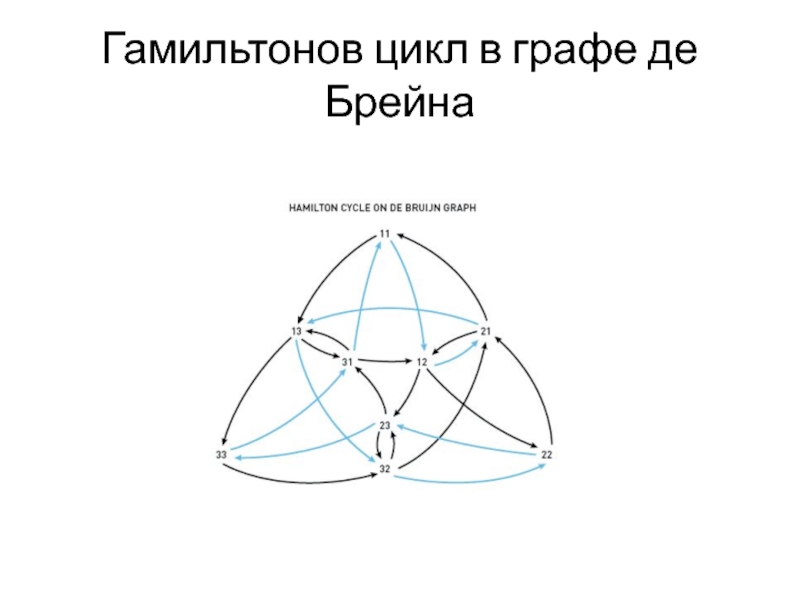
- 31. Гамильтонов цикл в графе де Брейна
- 32. Граф дорог – это цифровая векторная карта,
- 33. Яндекс – школа данныхЗадача о предсказании пробок
- 34. Метод деревьев решений (decision trees) является одним
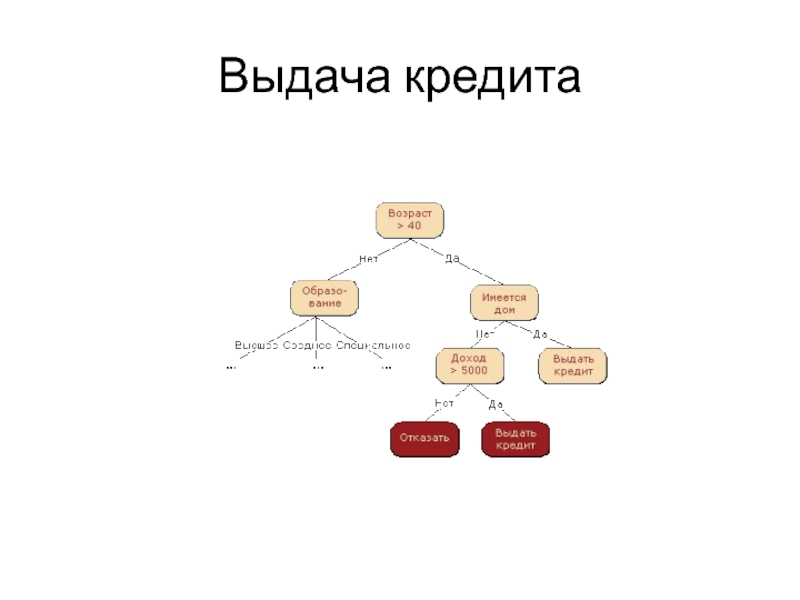
- 35. Выдача кредита
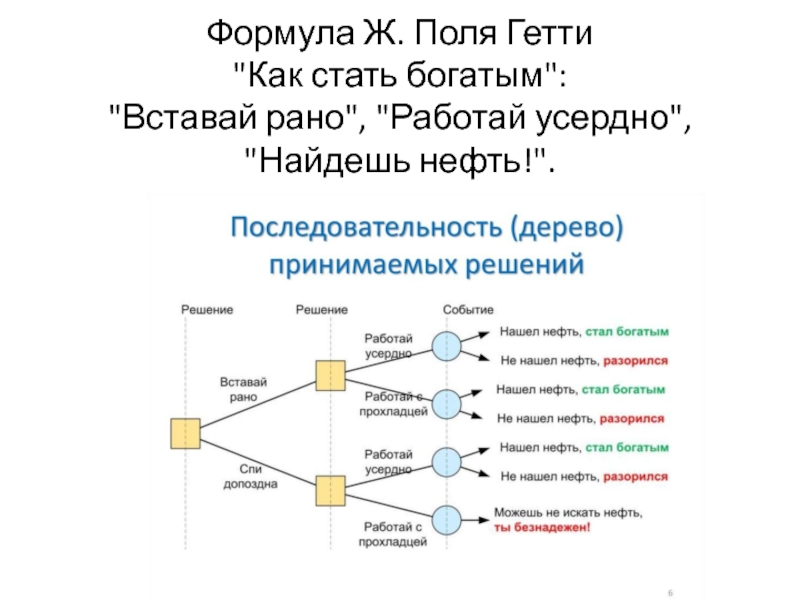
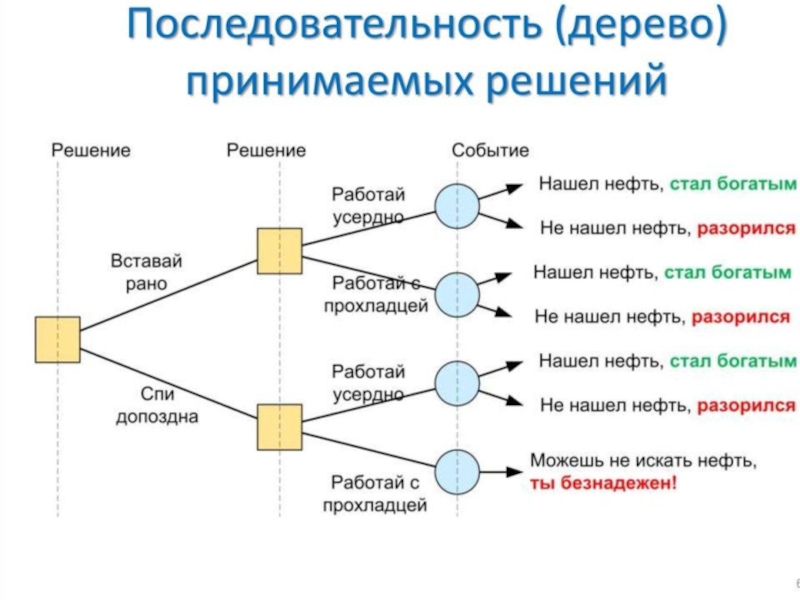
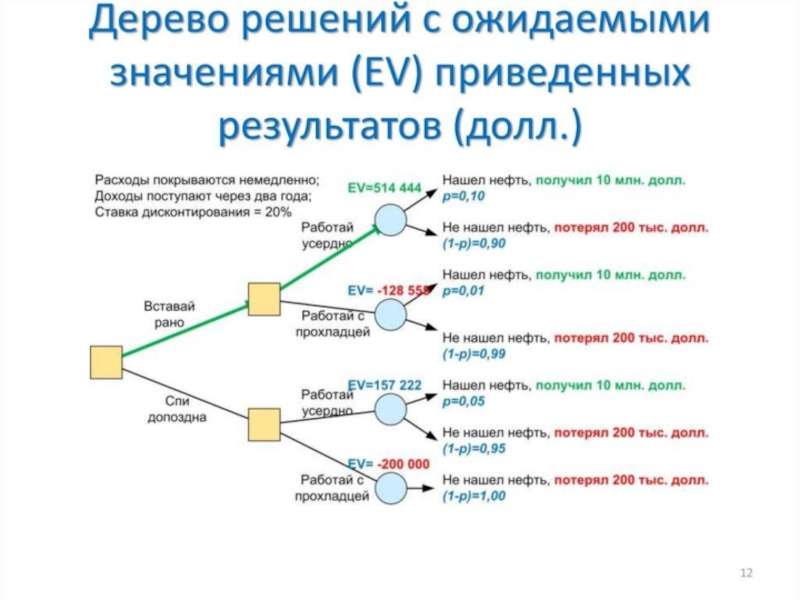
- 36. Формула Ж. Поля Гетти "Как стать богатым": "Вставай рано", "Работай усердно", "Найдешь нефть!".
- 37. Слайд 37
- 38. Слайд 38
- 39. Анализ больших данных. Поиск сообществ в графах.
- 40. Поиск сообществ в неориентированных графах (граф доменов
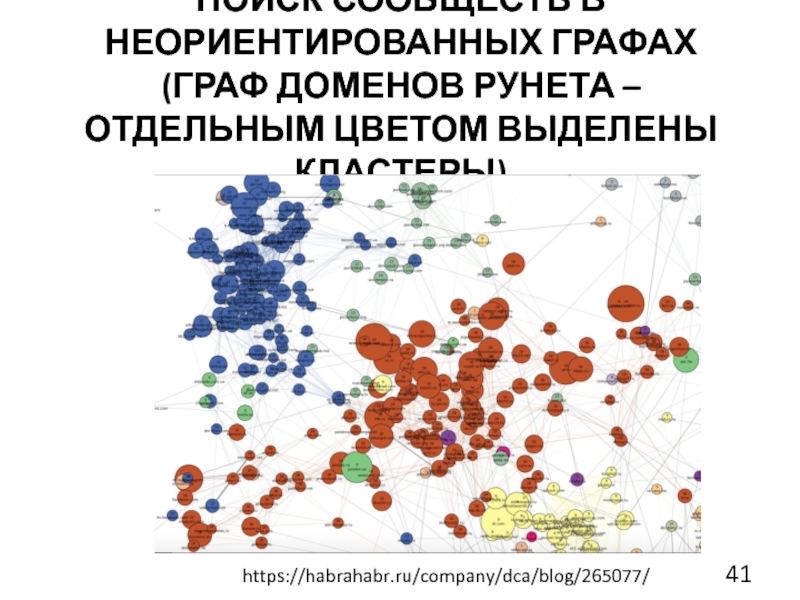
- 41. Поиск сообществ в неориентированных графах (граф доменов Рунета – отдельным цветом выделены кластеры) https://habrahabr.ru/company/dca/blog/265077/
- 42. Скачать презентанцию
«Отец» теории графов Леонард ЭйлерЗадача о семи мостах КенигсбергаПисьмо итальянскому математику и инженеру Маринони от 13 марта 1736 года. В этом письме Эйлер пишет о том, что он смог найти
Слайды и текст этой презентации
Слайд 2«Отец» теории графов
Леонард Эйлер
Задача о семи мостах Кенигсберга
Письмо итальянскому
математику и инженеру Маринони от 13 марта 1736 года.
В
этом письме Эйлер пишет о том, что он смог найти правило, пользуясь которым легко определить, можно ли пройти по всем мостам, не проходя дважды ни по одному из них (в случае семи мостов Кёнигсберга это невозможно).Слайд 4Если дана геометрическая фигура, как начертить ее на бумаге одним
росчерком пера, не проводя дважды ни одну линию?
Слайд 5Прикладные задачи
1847 год
Физик Густав Роберт Кирхгоф
Теория графов для исследования электрических
цепей
Множество фундаментальных циклов в графе
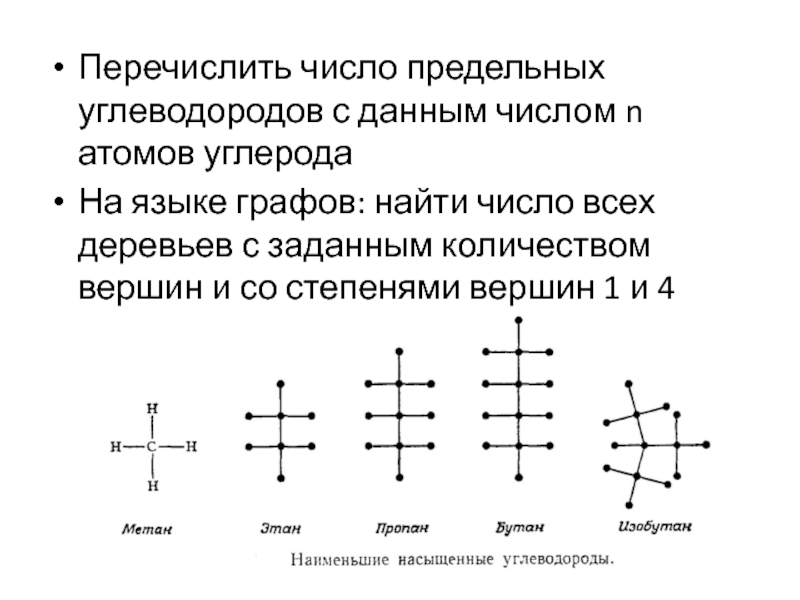
Слайд 7Перечислить число предельных углеводородов с данным числом n атомов углерода
На
языке графов: найти число всех деревьев с заданным количеством вершин
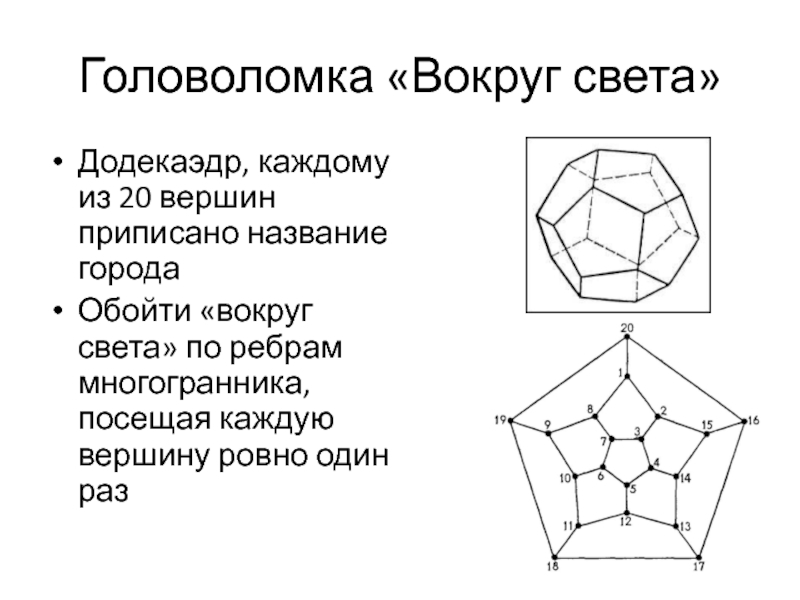
и со степенями вершин 1 и 4Слайд 9Головоломка «Вокруг света»
Додекаэдр, каждому из 20 вершин приписано название города
Обойти
«вокруг света» по ребрам многогранника, посещая каждую вершину ровно один
разСлайд 11Задача коммивояжера (англ. Travelling salesman problem, TSP) — задача, в которой коммивояжер
должен посетить N городов, побывав в каждом из них ровно по одному
разу и завершив путешествие в том городе, с которого он начал.В какой последовательности ему нужно обходить города, чтобы общая длина его пути была наименьшей?
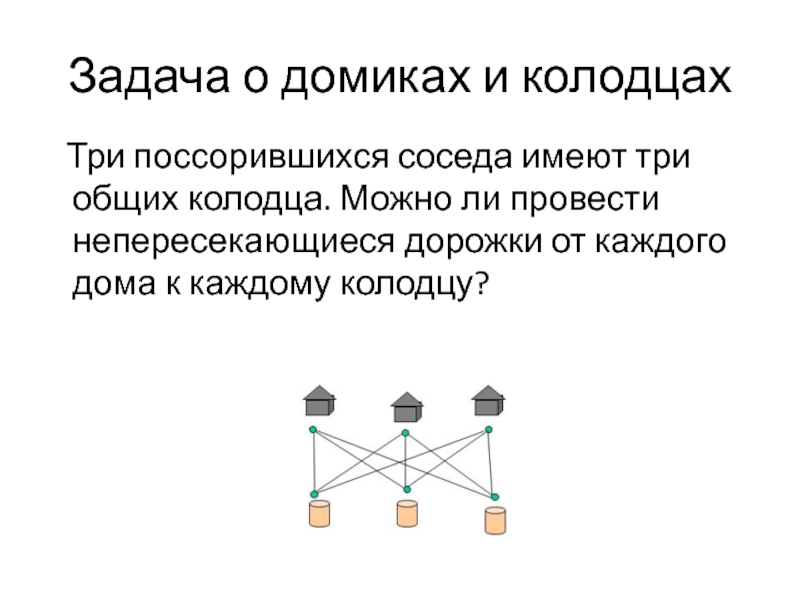
Слайд 12Задача о домиках и колодцах
Три поссорившихся соседа имеют
три общих колодца. Можно ли провести непересекающиеся дорожки от каждого
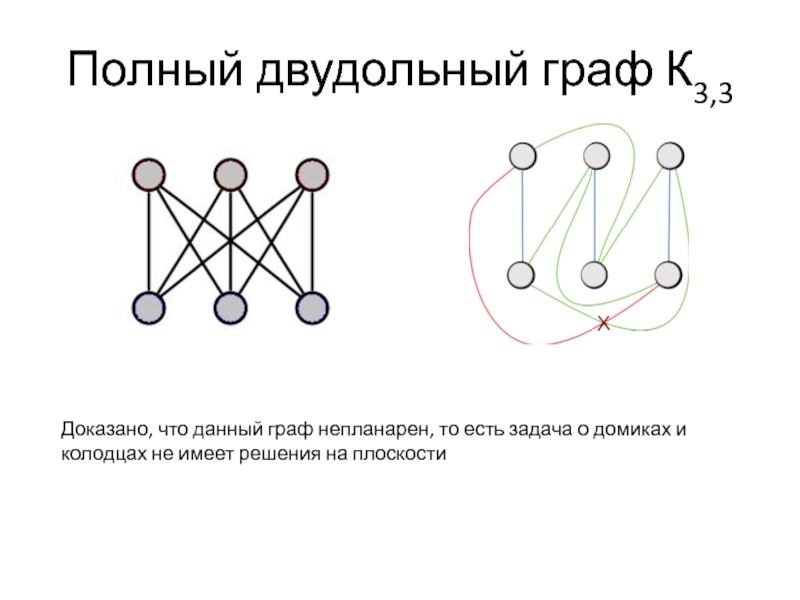
дома к каждому колодцу?Слайд 13Полный двудольный граф К3,3
Доказано, что данный граф непланарен, то есть
задача о домиках и колодцах не имеет решения на плоскости
Слайд 14Задача о раскраске карт или гипотеза о четырех красках
1850-1852 г.г.
(приблизительно) Ф.Гатри постановка задачи: «сколько потребуется красок для раскраски любой
плоской карты таким образом, чтобы никакие две смежные области не были окрашены в один и тот же цвет»Гипотеза: достаточно четырех красок
Слайд 15Задача о раскраске карт или гипотеза о четырех красках
1879 г.
британский математик Альфред Брей Кемпе дал ошибочное доказательство
1890 г. лектор
Дурхэмского университета Перси Джон Хивуд опровергнул доказательство Кемпе и показал, что гипотеза верна для пяти красок1925 г. Филипп Франклин, оставив в стороне общую проблему четырех красок, сумел доказать, что для раскрашивания любой карты, содержащей не более 25 областей, требуются только четыре краски.
1940 г. Винн распространил доказательство на карты с 35 областями
1970 г. Оре и Стемпл увеличили число областей до 39
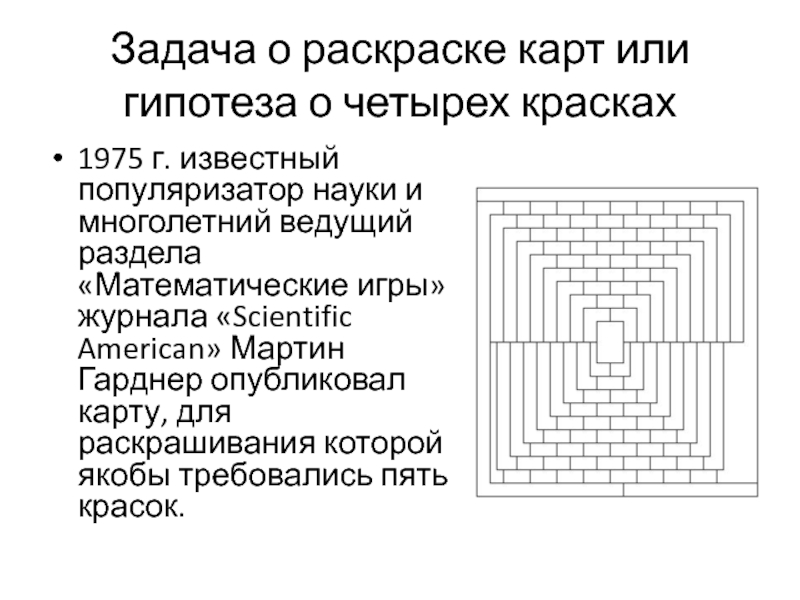
Слайд 161975 г. известный популяризатор науки и многолетний ведущий раздела «Математические игры»
журнала «Scientific American» Мартин Гарднер опубликовал карту, для раскрашивания которой
якобы требовались пять красок.Задача о раскраске карт или гипотеза о четырех красках
Слайд 171976 г. два математика из Иллинойского университета, Вольфганг Хакен и Кеннет
Аппель, предложили новый метод, перевернувший традиционные представления о математическом доказательстве.
Хакену
и Аппелю удалось свести проблему четырех красок «всего лишь» к 1482 конфигурациям, служащим теми строительными блоками, из которых можно составить любую карту. В июне 1976 года, затратив 1200 часов машинного времени, Хакен и Аппель заявили во всеуслышание, что им удалось проанализировать все 1482 карты и для раскрашивания ни одной из них не требуется более четырех красок.
Задача о раскраске карт или гипотеза о четырех красках
Слайд 18Примеры
Вершины – города, ребра - дороги между ними
Вершины – города,
ребра – наличие авиарейса
Вершины – люди, ребра - отношение «знакомы
между собой»Вершины – спортсмены, ребра – отношение «играли между собой»
Слайд 19Теория графов в игре престолов
https://habrahabr.ru/post/302936/
Граф социальной активности
Вершинам соответствуют персонажи; размер
вершины зависит от сказанных данным персонажем слов
Ребра - диалоги персонажей;
толщина ребра зависит от количества состоявшихся разговоров.
Слайд 21Общие сведения о графе
Граф неориентированный.
Вершин (персонажей): 1105
Рёбер (диалогов): 3505
5 книг,
почти 2 миллиона слов.
Для сбора данных было привлечено машинное обучение (точность
определения принадлежности разговора составляет около 75%).
Слайд 22Алгоритмы на графе
Подсчет степеней вершин – самые многосвязные персонажи
Диаметр графа
(расстояние между наиболее удаленными вершинами графа) равен 8
Поиск путей:
77 персонажей находятся «в центре» графа, иными словами они могут связаться с любым другим персонажем не более чем через 4х другихСлайд 25 Математическая модель интернета – веб-граф (А.Райгородский)
http://elementy.ru/nauchno-populyarnaya_biblioteka/431792/Matematicheskie_modeli_interneta
Вершинами этого
графа будут сайты, и между двумя вершинами A, B мы проведем столько ребер,
направленных от A к B, сколько есть ссылок с сайта A на сайт B, и столько ребер, направленных от B к A, сколько есть ссылок с сайта B на сайт A.Слайд 26Свойства веб-графа
Диаметр веб-графа равен 6 (закон шести рукопожатий)
Веб-граф является достаточно
разреженным: если вершин у веб-графа n, то ребер у него не более mn с некоторым
постоянным m ≥ 1Таким образом, несмотря на кажущуюся хаотичность в процессе образования интернета, есть весьма жесткие статистические ограничения, которым он годами подчиняется. Почему это так? Что стоит за всеми свойствами интернета? Каковы законы, управляющие формированием сети?
Слайд 27Алгоритм PageRank
PageRank был представлен и опубликован Сергеем Брином (Sergey Brin) и Ларри
Пейджем (Larry Page) на седьмой международной конференции World Wide Web (WWW7)
в апреле 1998 года.Это алгоритм ранжирования с использованием гиперссылок в Интернете. На основе алгоритма, они построили поисковую систему Google
PageRank — это числовая величина, характеризующая «важность» веб-страницы. Чем больше ссылок на страницу, тем она становится «важнее». Таким образом, PageRank — это метод вычисления веса страницы путём подсчёта важности ссылок на неё.
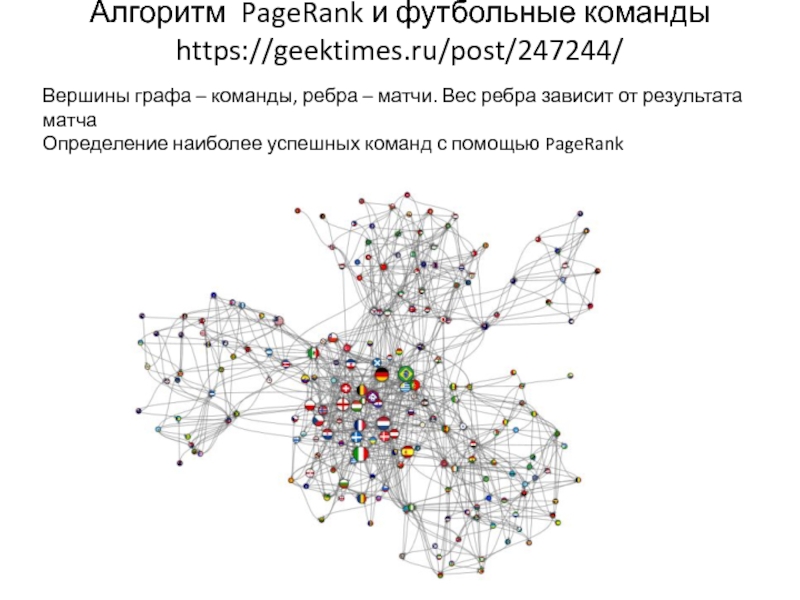
Слайд 28Алгоритм PageRank и футбольные команды
https://geektimes.ru/post/247244/
Вершины графа – команды, ребра
– матчи. Вес ребра зависит от результата матча
Определение наиболее успешных
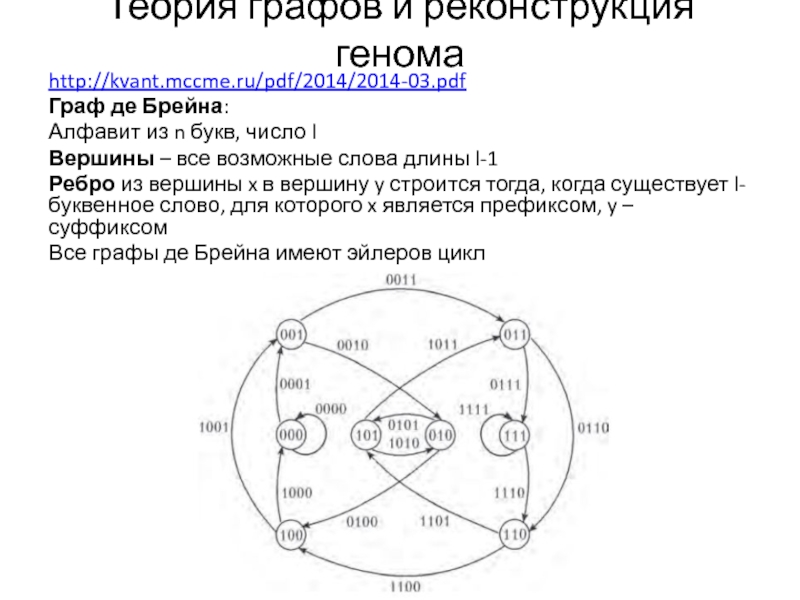
команд с помощью PageRankСлайд 29Теория графов и реконструкция генома
http://kvant.mccme.ru/pdf/2014/2014-03.pdf
Граф де Брейна:
Алфавит из n букв,
число l
Вершины – все возможные слова длины l-1
Ребро из
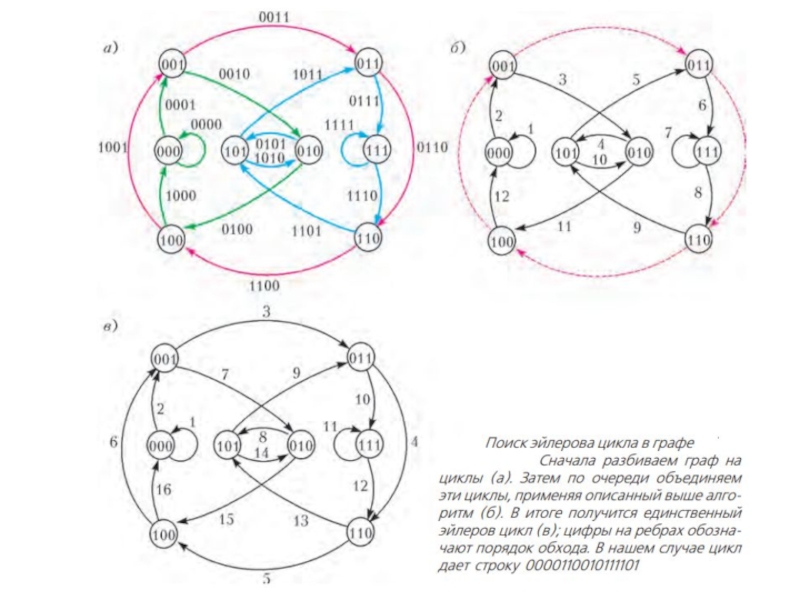
вершины x в вершину y строится тогда, когда существует l-буквенное слово, для которого x является префиксом, y – суффиксомВсе графы де Брейна имеют эйлеров цикл
Слайд 32Граф дорог – это цифровая векторная карта, состоящая из топологически
связанных дуг и узлов, местоположение и свойства которых с заданной
точностью и полнотой передают маршруты и организацию движения наземного транспорта.http://www.gisinfo.ru/products/editroad.htm
Слайд 33Яндекс – школа данных
Задача о предсказании пробок на небольшой промежуток
времени
вперед http://imat2010.yandex.ru/
Данные
Граф дорог. Перекрестки Москвы соответствуют вершинам
графа, а отрезки улиц
— дугамДанные о пробках (загруженности дорог) Наблюдения
охватывают 31 день. Для первых 30 дней в файле
содержится информация о скорости движения потока
автотранспорта с 16:00 до 22:00; для последнего дня — с
16:00 до 18:00.
Слайд 34Метод деревьев решений (decision trees) является одним из наиболее популярных
методов решения задач классификации и прогнозирования.
Иногда этот метод Data Mining также
называют деревьями решающих правил, деревьями классификации и регрессии.Банковское дело. Оценка кредитоспособности клиентов банка при выдаче кредитов.
Промышленность. Контроль за качеством продукции (выявление дефектов), испытания без разрушений (например проверка качества сварки) и т.д.
Медицина. Диагностика различных заболеваний.
Молекулярная биология. Анализ строения аминокислот.
Слайд 36Формула Ж. Поля Гетти "Как стать богатым": "Вставай рано", "Работай
усердно", "Найдешь нефть!".
Слайд 39Анализ больших данных. Поиск сообществ в графах. Задачи кластеризации
Выделение сообществ (кластеров) разных объектов: пользователей, сайтов, продуктовых
страниц интернет-магазинов:Выделение сегментов пользователей для проведения рекламных кампаний.
Использование кластеров в качестве предикторов (прогностический параметр, средство прогнозирования) в персональных рекомендациях
Снижение размерности в любой задаче машинного обучения.
Сличение товарных URL между различными интернет-магазинами с целью выявления среди них групп, соответствующих одному и тому же товару.
Компактная визуализация — человеку будет проще воспринимать структуру данных.