Слайд 2Метод итераций
Часто в практических задачах нет необходимости находить точное решение
матричной игры. Достаточно найти приближённое решение, которое даёт средний выигрыш,
близкий к цене игры и приближённые оптимальные стратегии игроков.
Ориентировочное значение цены игры может дать уже простой анализ матрицы выигрышей и определение нижней и верхней цен игры. Если они близки, то поисками точного решения заниматься не обязательно, так как достаточно выбрать чистые минимаксные стратегии. Если же они не близки, можно получить приемлемое для практики решение с помощью численных методов решения игр, из которых рассмотрим метод итераций (метод Робинсон).
Слайд 3Суть метода
Пусть разыгрывается матричная игра с матрицей А={aij} размера (m×n).
Идея метода – многократное фиктивное разыгрывание игры с заданной матрицей.
Одно разыгрывание игры будем называть партией, число которых неограниченно.
В 1-ой партии оба игрока выбирают совершенно произвольные чистые стратегии. Пусть игрок 1 выбрал i-ю стратегию, а игрок 2 – j-ю стратегию. Во второй партии игрок 1 отвечает на ход игрока 2 той своей стратегией, которая даёт ему максимальный выигрыш. В свою очередь, игрок 2, отвечает на этот ход игрока 1 своей стратегией, которая обращает его проигрыш в минимум. Далее третья партия.
С ростом числа шагов процесса смешанные стратегии, которые приписываются игрокам, приближаются к их оптимальным стратегиям. Этот процесс приближённого нахождения оптимальных стратегий игроков называется итеративным , а его шаги – итерациями.
Слайд 4Пример
Найти приближённое решение игры с матрицей
Слайд 5Решение
Пусть игру начнёт игрок 2. Он произвольно выбирает одну из
своих чистых стратегий. Предположим, что он выбрал свою 1-ю стратегию,
а игрок 1 отвечает своей 2-й стратегией. Занесём данные в таблицу.
Слайд 6
Первая партия
В столбце υ находится наибольший средний выигрыш 4 игрока
1, полученный им в первой партии; в столбце ω стоит
наименьший средний проигрыш 1, полученный игроком 2 в первой партии; в столбце ν находится среднее арифметическое ν=(υ+ω)/2=5/2, т. е. приближенное значение цены игры, полученное в результате проигрывания одной партии.
Так как игрок 1 выбрал 2-ю стратегию, то игрок 2 может проиграть:
4, если применит свою 1-ю стратегию;
1, если применит свою 2-ю стратегию;
2, если применит свою 3-ю стратегию.
Поскольку он желает проиграть как можно меньше, то в ответ применит свою 2-ю стратегию.
Слайд 7Вторая партия
Тогда первый игрок получит выигрыш равный 3, 1, 0
соответственно при своих 1-й, 2-й, 3-й стратегиях, а его суммарный
выигрыш за две партии составит:
0+3=3 при его 1-й стратегии;
4+1=5 при его 2-й стратегии;
2+0=2 при его 3-й стратегии.
Из всех суммарных выигрышей наибольшим является 5, который получается при 2-й стратегии игрока 1. Значит, в этой партии он должен выбрать именно эту стратегию.
Слайд 8Конец второй партии
При 1-й стратегии игрока 1 игрок 2 проигрывает
4, 1, 2 соответственно 1-й, 2-й, 3-й его стратегиям, а
суммарный проигрыш за обе партии составит:
4+4=8 при его 1-й стратегии;
1+1=2 при его 2-й стратегии;
2+2=4 при его 3-й стратегии.
Все полученные данные занесём в таблицу. В столбец υ ставится наибольший суммарный выигрыш игрока 1 за две партии, деленный на число партий, т. е. 5/2; в столбец ω ставится наименьший суммарный проигрыш игрока 2, деленный на число партий, т. е. 2/2; в столбец ν ставится среднее арифметическое этих значений, т. е. 7/2.
Слайд 9Таблица
В третьей партии игрок 2 выбирает свою 2-ю стратегию, так
как из всех суммарных проигрышей наименьшим является 2.
Таким образом, продолжая
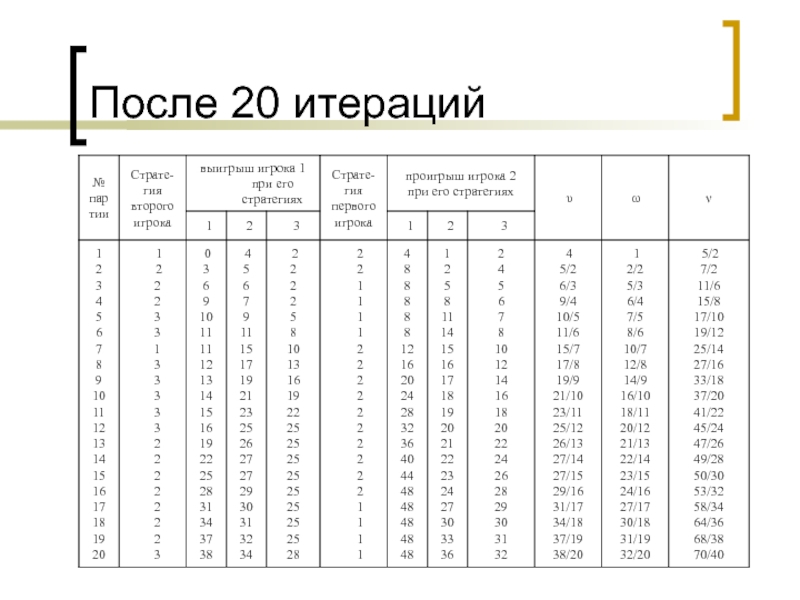
этот процесс далее, составим таблицу разыгрываний игры за 20 итераций (партий).
Слайд 11Приближенное решение
Из таблицы видно, что в 20-ти проигранных партиях стратегии
1, 2, 3 для второго игрока встречаются соответственно 2, 10,
8 раз, следовательно, их относительные частоты равны 2/20, 10/20, 8/20. Стратегии 1, 2, 3 для игрока 1 встречаются соответственно 8, 12, 0 раз, следовательно, их относительные частоты равны 8/20, 12/20, 0, а приближённое значение цены игры равно 70/40.
Таким образом, получили приближённое решение игры: x20=(1/10,1/2,2/5), y20=(2/5,3/5,0), ν=1,57.
Слайд 12Заключение
Такой итеративный процесс ведёт игроков к цели медленно. Часто для
получения оптимальных стратегий, дающих игрокам выигрыш, приходится проделывать сотни итераций.
При этом скорость сходимости заметно ухудшается с ростом размерности матрицы и ростом числа стратегий игроков. Поэтому, практическая ценность этого метода имеет место, когда вычисления проводятся на достаточно быстродействующих вычислительных машинах. Но наряду с таким недостатком можно выделить и достоинства метода итераций:
Этот метод даёт возможность найти ориентировочное значение цены игры и приближённо вычислить оптимальные стратегии игроков.
Сложность и объём вычислений сравнительно слабо возрастают по мере увеличения числа стратегий игроков (m и n).
Слайд 13Задание
Найти решение игр итерационным методом
Слайд 14Задание
Найти решение игр графо-аналитическим методом