Теория Информации

Substitution ciphers: Simple transposition. Product cipher. Simple substitution

cipher. Caesar cipher. Vigener cipher.
Mono and Poly alphabetic substitution cipher: Playfair cipher.
Rotor machines. The Enigma: a unique rotor machine.
Data Encryption Standard (DES): History of the DES. DES algorithms.Weak and semi weak keys. Advanced DES versions. IDEA. Blowfish.
Advanced Encryption Standard (AES): Reindgiil Algorithm.
Number theory: Prime numbers. Euler’s function. Euler’s theorem. Congruence.
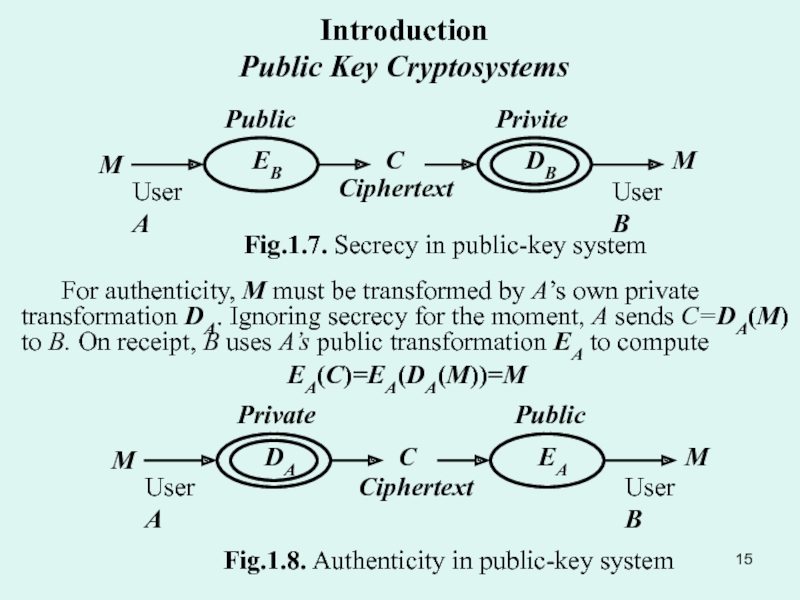
Public Key Cipher: Principles of the public key cipher. One-way function. Deffie and Hellman algorithm.

Practical aspects.
Linear Feedback Shift Register: Pseudorandom key generation by LFSR.

M- sequences.
Stream cipher: Synchronous stream ciphers. Self- synchronizing cipher.
Cryptographic Keys Management: Keys generation, distribution and athetifacation of Public Keys
Communication Security: Transport Layer Security (TLS) and its predecessor, Secure Sockets Layer (SSL).
Authentication Protocols: Password- authentication key agreement protocols. Password Authentification Protocol (PAP)

cryptosystem.
Hash Functions: Message authentication codes (MAC). MD5. SHA-1.
Digital Signature

algorithms: RSA based digital signature. Digital Signature Standard (DSS). ElGamal signature scheme.
Digital Signature algorithms modifications: Blind signature. Group signature. Proxy signature.
Elliptic curve cryptography: Elliptic curve cryptosystem (ECC). Elliptic curve Diffie-Hellman algorithm. Elliptic curve Menezes-Qu-Vanstone cryptosystem.
Elliptic Curve Digital Signature Algorithm: ECDSA algorithm.
Quantum Cryptography: Quantum Key Distribution. BB84, B92, Entanglement-Based quantum fey distribution.

oscillator PUF. SRAM based PUF.
Steganography: Textual steganography. Graphical steganography.

LSB, BPCS, ABCDE and PCT steganography.
Watermarking and Fingerprinting: Patchwork method. Copyright Protection Watermarking for copy protection
Software protection: Software watermarking, obfuscation, and tamper-proofing. Software dongle. Electronic keys.
E-Commerce security: E-commerce security standards. SET protocol.
Internet Banking security: Online Banking Security. Password and PIN security:

/ Ю.В. Романец, П.А. Тимофеев, В.Ф. Шаньгин. – М.: Радио

и связь, 1999. – 328 с.
2. Харин, Ю.С. Математические и компьютерные основы криптологии / Ю.С. Харин, В.И. Берник, Г.В. Матвеев, С.В. Агиевич. – Минск : Новое Знание, 2003. – 382 с.
3. Шнайер, Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си / Б. Шнаейр. – М. : ТРИУМФ, 2002. – 816 с.
4. Ярмолик, В.Н. Элементы теории информации. Практикум для студентов специальности “Программное обеспечение информационных технологий” / В.Н. Ярмолик, А.П. Занкович, С.С. Портянко. – Минск : БГУИР, 2007. – 40 с.
5. Ярмолик, В.Н. Криптография, стеганография и охрана авторского права / В.Н. Ярмолик, С.С. Портянко, С.В. Ярмолик. – Минск : Издательский центр БГУ, 2007. – с.
6. Грибунин, В.Г. Цифровая стеганография / В.Г. Грибунин, И. Н. Оков, И. В. Туринцев. – М. : СОЛОН-Пресс, 2002. – 272 с.

is a secret method of writing, whereby plaintext (or cleartext)

is transformed into ciphertext (cryptogram).
Encipherment (encryption) is the process of transforming plaintext into ciphertext.
Decipherment (decryption) is the reverse process of transforming ciphertext into plaintext. Both encipherment and decipherment are controlled by a cryptographic key or keys.

Introduction

ciphers rearrange bits or characters.
The following simple example of

the “rail-fence” cipher illustrate this method.

Fig.1.2. Rail-fence transposition cipher

Introduction Transposition ciphers

characters with substitutes.

A simplest type of substitution cipher shifts

each letter in the English alphabet forward by k positions cyclically (shifts past Z cycle back to A). k is the key to the cipher. This type of cipher is often called a Caesar cipher.

Fig.1.3. Caesar’s substitution cipher

ABCDEFGHIJKLMNOPQRSTUVWXYZ

(or privacy),
to prevent the unauthorized disclosure of data; and

authenticity
or integrity), to prevent the unauthorized modification of data.

components:
1. A plaintext message space, M.
2. A cipher message space,

C.
3. A key space, k.
4. A family of enciphering transform., Ek: M --> C.
5. A family of deciphering transform., Dk: C --> M.

Cryptosystems General Requirements
1. The system must be easy to use.
2. The enciphering and deciphering transformations must be efficient for all keys.
3. The security of the system should depend only on the secrecy of the keys and not on the secrecy of the algorithms E and D.

infeasible for a cryptanalyst to systematically determine the deciphering transformation

Dk from intercepted ciphertext C, even if the corresponding plaintext M is known.
2. It should be computationally infeasible for a cryptanalyst to systematically determine plaintext M from intercepted ciphertext C.
Authenticity Requirements
1. It should be computationally infeasible for a cryptanalyst to systematically determine the enciphering transformation Ek given C even if the corresponding plaintext M is known.
2. It should be computationally infeasible for a cryptanalyst to systematically find ciphertext C’ such that Dk (C’) is valid plaintext in the set M.

asymmetric (two-key).
In symmetric or one-key cryptosystems the enciphering and

deciphering key are the same (or easily determined from each other). This means the transformations Ek and Dk are also easily derived from each other. Until recently, all cryptosystems were one-key systems only. There are also usually referred to as conventional (or classical) systems.
One-key systems provide an excellent way of enciphering user’s privite files. Each user A has private transformations Ek and Dk for enciphering and deciphering files.

transformation EA, which may be registered with a public directory,

and a private transformation DA, which is known only to that user.
The private transformation DA is described by a private key, and the public transformation EA by a public key derived from the private key by one-way transformation. It must be computational infeasible to determine DA from EA (or even to fined a transformation equivalent to DA).
In a public-key system, secrecy and authenticity are provided by the separate transformations. Suppose user A wishes to send a message M to another user B. If A knows B’s public transformation EB, A can transmit M to B in secrecy by sending the ciphertext C=EB (M). On receipt, B deciphers C using B’s private transformation , getting

DB(C)=DB(EB(M))=M.

Introduction
Public Key Cryptosystems

A’s own private transformation DA. Ignoring secrecy for the moment,

A sends C=DA(M) to B. On receipt, B uses A’s public transformation EA to compute
EA(C)=EA(DA(M))=M

Fig.1.8. Authenticity in public-key system

must each apply two sets of transformations. Sender A generates

a ciphertext C=EB(DA(M)), and B recovers M according to

EA(DB(C))=EA(DB(EB(DA(M))))= EA(DA(M))=M.

M

C

M

secrecy

User A

User B

DA

Private

EB

Public

DB

Private

EA

Public

authenticity

Fig.1.9. Secrecy and Authenticity in public-key system

Introduction
Public Key Cryptosystems