Теория сетей Петри и моделирование систем РТУ МИРЭА Лекция 3

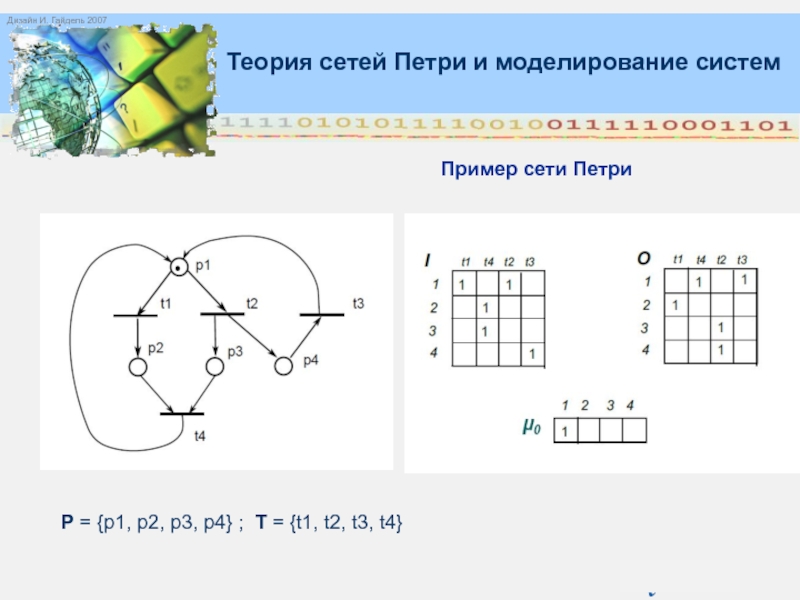
(СП) - это двудольный ориентированный мультиграф N = (P, T,

I, O, µ0), где:
P - конечное непустое множество элементов, называемых позициями; T - конечное непустое множество элементов, называемых переходами; I: PT{0,1,2...} и O: PT{0,1,2...} - функции инцидентности;
µ0 : P{0,1,2...} - начальная разметка.

n =P- мощность множества P,
m =T - мощность множества T.
 
СП обычно представляют в виде геометрического объекта. При этом позиции изображают кружками, переходы - черточками или прямоугольниками.

Дуга проводится от позиции pi к переходу tj, если I(pi, tj) > 0, и от перехода tj к позиции pi, если O( pi, tj) > 0.

Основные определения и обозначения

)

позицию pi с переходом tj, определяется величиной I(pi, tj). Аналогично

кратность дуги, соединяющей переход tj с выходной позицией pi, определяется величиной O(pi, tj).

Кратность рассматривается как возможность дублирования дуги, соединяющей вершины pi и tj (или tj и pi ), I(pi, tj) (или O(pi, tj)) раз.
 
Если I(pi, tj) > 0, то позицию pi называют входной к переходу tj, а переход tj - выходным к позиции pi.

Множество входных позиций (pre(tj)) к переходу tj определяется как
pre(tj)={ pI(pi, tj) > 0}, а множество выходных переходов (post(pi )) к позиции pi - как post(pi)={ t  I(pi, tj) > 0} .

Основные определения и обозначения

)

называют входным к позиции pi, а позицию pi - выходной

к переходу tj .

Множество входных переходов к позиции pi определяется как
pre(pi)={t | O(pi, tj) > 0},
а множество выходных позиций к переходу tj - как
post(tj)={p | O(pi, tj) > 0}.

Входная позиция pi к переходу tj называется головной, если pre(pi) =  . Аналогично выходная позиция pi к переходу tj называется хвостовой, если post(pi) =  .

Основные определения и обозначения

)

Теория сетей Петри и моделирование систем

N = (P, T, I, O, µ0 ), для

которой T={t};

P={p',p''}; pre(t)={p'}, post(t) = {p''}; = (0,0).

Основные определения и обозначения

= (0,0).

µ0

Теория сетей Петри и моделирование систем

разметка представляет собой функцию  : P{0,1,2...}. Переход может сработать

при разметке , если он активен.

Переход tj является активным, если pi  pre(tj): (pi ) >= I( pi, tj) .

В результате срабатывания перехода tj разметка меняется в соответствии со следующим правилом:
pi  (pre( tj)  post(tj)) : ‘(pi ) = (pi ) - I(pi, tj) + O( pi, tj) .

В этом случае говорят, что разметка ‘ достижима от разметки  в результате срабатывания перехода tj, а разметка  предшествует ‘.
СП останавливается, если при некоторой разметке не может сработать ни один из ее переходов. Такая разметка называется тупиковой.

Таким образом, СП моделируют некоторую структуру и динамику ее функционирования.

Основные определения и обозначения

= (0,0).

Теория сетей Петри и моделирование систем

; T = {t1, t2, t3, t4}
Теория сетей Петри

и моделирование систем

обобщением СП и служат для моделирования иерархических систем, которые наряду

с неделимыми, атомарными компонентами содержат составные компоненты, представляющие собой отдельные подсистемы. Для определения ИСП множество переходов разбивается на подмножества простых и иерархических переходов (ИПР). Простым переходам соответствуют элементарные сети. ИПР представляет собой некоторый фрагмент СП.

Сравнительный анализ выразительных свойств ИСП и СП показывает, что введение иерархии в сетевые модели существенно улучшает моделирующие способности СП-моделей.

Теория сетей Петри и моделирование систем

является то, что нельзя отметить срабатыванием перехода факт изменения разметки

с ненулевого значения на нулевое. Таким образом из двух альтернатив
(p)  0 и (p) = 0, содержащихся в операторе условного вычитания единицы, в СП можно представить только одну, первую, но нельзя отразить проверку на ноль, так как сеть не может реагировать непосредственно на отсутствие метки в позиции. В результате было показано, что СП не могут моделировать машины Минского и Тьюринга.

Флинн и Аджервала модифицировали СП, введя в них специальные ингибиторные дуги, осуществляющие проверку на нулевую разметку, и показали, что получаемое обобщение дает класс сетей равномощных машине Тьюринга.

Теория сетей Петри и моделирование систем

FI:PT{0,1}, которая вводит ингибиторные дуги для тех пар (p,t), для

которых FI(p,t) = 1.

Ингибиторные дуги связывают только позиции с переходами и на рисунках изображаются заканчивающимися не стрелками, а маленькими кружочками. Правило срабатывания перехода в ингибиторной сети модифицируется следующим образом:

 pi  pre(tj): ( pi )  I( pi, tj) & (pi )FI(p,t) = 0 .

Модификации сетей Петри (ингибиторные сети)

Теория сетей Петри и моделирование систем

может сработать несколько переходов, то срабатывает любой из них. В

реальных дискретных системах имеют место ситуации, когда из двух готовых сработать устройств требуется запустить вначале одно, а затем другое. Иными словами, одно из устройств имеет приоритет на запуск перед другим. Эти ситуации не моделируются в СП.

Модифицируем определение СП следующим образом. Введем множество PR, элементы которого частично упорядочены отношением "" (меньше или равно). С каждым переходом t СП свяжем его приоритет pr(t), принадлежащий множеству PR.

Модификации сетей Петри (приоритетные сети)

Теория сетей Петри и моделирование систем

сработать при разметке  , если для любого другого перехода

t' этой сети, который также может сработать при разметке , pr(t')pr(t).

Другими словами, если несколько переходов готовы сработать, то срабатывает такой переход, приоритет которого не меньше приоритетов остальных готовых к срабатыванию переходов. Такую модификацию СП называют приоритетными сетями.

Показано, что класс приоритетных СП является строго мощнее СП и равномощен классам машин Тьюринга и Минского.

Модификации сетей Петри (приоритетные сети)

Теория сетей Петри и моделирование систем

моделируемых событий. Предлагаемое расширение СП позволяет отразить в модели временные

параметры системы. При этом фактор времени учитывается путем введения задержки между моментом изъятия меток из входных позиций сработавшего перехода и моментом помещения меток в выходные позиции данного перехода.

Очевидно, что определенные таким образом временные СП могут использоваться в тех случаях, когда возможно предположение о постоянном времени протекания каждого процесса в модели.

Модификации сетей Петри (временные сети)

Теория сетей Петри и моделирование систем

современной литературе встречается ряд других расширений СП, которые учитывают специфику

той предметной области, в которой используется аппарат СП.

Среди данных расширений можно выделить стохастические СП, раскрашенные СП, Е-сети, СП для описания процедур принятия решений (нейронные, нечеткие, числовые, абстрактные) и другие.

Теория сетей Петри и моделирование систем