Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория вероятностей
Содержание
- 1. Теория вероятностей
- 2. Теория вероятностей Теория вероятностей
- 3. Классическое определение вероятностиПьер Симон Лаплас (1749-1827)Отношение числа
- 4. Формула вероятностиР - от первой буквы французского
- 5. Пример. Подбрасываем две одинаковые монеты. Какова вероятность
- 6. Ошибка Даламбера. Великий французский философ
- 7. Свойства вероятности.Вероятность достоверного события равнаВероятность невозможного события
- 8. Свойства вероятности.P(U) = 1 (U – достоверное
- 9. Практикум по решению задач. Задача 1. Наблюдения
- 10. Вероятность в демографииПьер Симон Лаплас (1749-1827)Александр фон Гумбольдт (1769-1859)
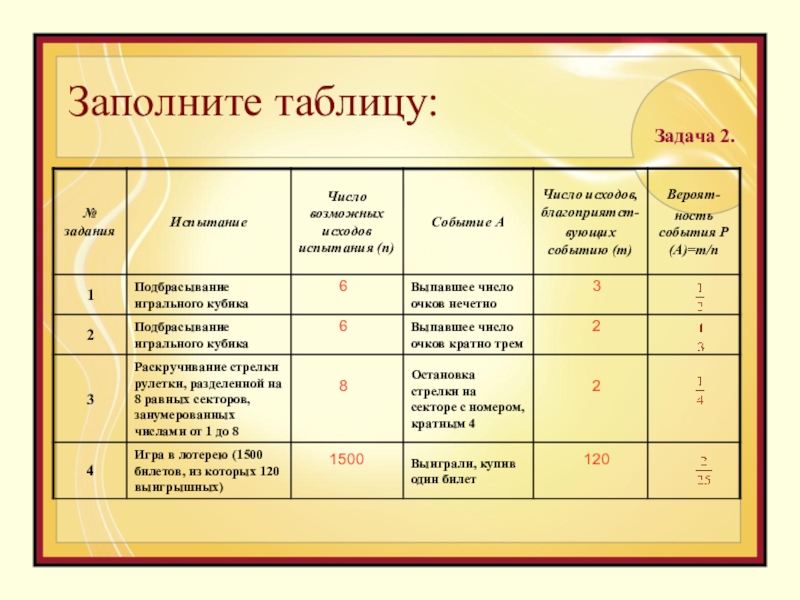
- 11. Заполните таблицу:6681500322120Задача 2.
- 12. Практикум по решению задач. При игре в
- 13. Вероятность: P(A)=6/36= =1/6.Решение. Составим таблицу.
- 14. стакатистиПрактикум по решению задач. Из карточек составили
- 15. Решение.В слове «статистика» всего 10 букв.Буква «с»
- 16. Практикум по решению задач. В коробке 4
- 17. Решениеа) Мы имеем всевозможных случаев 9. Благоприятствующих
- 18. Практикум по решению задач. На четырех карточках
- 19. Практикум по решению задач. Задача 7. При
- 20. Использованные источникиЯ. Перельман. Занимательная геометрия на вольном
- 21. Скачать презентанцию
Теория вероятностей Теория вероятностей - раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.
Слайды и текст этой презентации
Слайд 3Классическое определение вероятности
Пьер Симон Лаплас
(1749-1827)
Отношение числа событий, благоприятствующих появлению
события А, к общему числу событий пространства, называют вероятностью события
А и обозначают Р(А).
Слайд 4Формула вероятности
Р - от первой буквы французского слова probabilite –
вероятность.
m – количество благоприятных событий
n – общее число событий пространства
Слайд 5Пример. Подбрасываем две одинаковые монеты. Какова вероятность того, что они
упадут на одну и ту же сторону?
Решение № 1.
Опыт имеет
триравновозможных исхода:
1) обе монеты упадут на «орла»;
2) обе монеты упадут на «решку»;
3) одна из монет упадет на «орла», другая на «решку».
Из них благоприятными
будут два исхода.
Решение № 2.
Опыт имеет четыре
равновозможных исхода:
1) обе монеты упадут на «орла»;
2) обе монеты упадут на «решку»;
3) первая монета упадет на «орла», вторая на «решку»;
4) первая монета упадет на «решку», вторая на «орла».
Из них благоприятными будут
два исхода.
Слайд 6Ошибка Даламбера.
Великий французский философ и математик Даламбер
вошел в историю теории вероятностей со своей знаменитой ошибкой, суть
которой в том, что он неверно определил равновозможность исходов в опыте всего с двумя монетами!Жан Лерон Даламбер
(1717 -1783)
Слайд 7Свойства вероятности.
Вероятность достоверного события равна
Вероятность невозможного события равна
Вероятность события А
не меньше , но не больше
1
0
0
1
Слайд 8Свойства вероятности.
P(U) = 1 (U – достоверное событие);
P(V) = 0
(V – невозможное событие);
0 P(A) 1.
Слайд 9Практикум по решению задач.
Задача 1.
Наблюдения показывают, что в
среднем среди 1000 новорожденных детей 514 мальчиков. Какова вероятность рождения
мальчика в такой серии наблюдений?Решение.
А – {Рождение мальчика}
n – количество благоприятных событий
m – общее количество событий
Слайд 12Практикум по решению задач.
При игре в нарды бросают
2 игральных кубика. Какова вероятность того, что на обоих кубиках
выпадут одинаковые числа?Задача 3.
Слайд 14с
т
а
к
а
т
и
с
т
и
Практикум по решению задач.
Из карточек составили слово «статистика». Какую
карточку с буквой вероятнее всего вытащить? Какие события равновероятные?
Задача 4.
Слайд 15Решение.
В слове «статистика» всего 10 букв.
Буква «с» встречается 2 раза
– P(С) = 2/10 = 1/5;
буква «т» встречается 3 раза
– P(Т) = 3/10;буква «а» встречается 2 раза – P(А) = 2/10 = 1/5;
буква «и» встречается 2 раза –P(И) = 2/10 = 1/5;
буква «к» встречается 1 раз – P(К) = 1/10.
Слайд 16Практикум по решению задач.
В коробке 4 синих, 3 белых
и 2 желтых фишки. Они тщательно перемешиваются, и наудачу извлекается
одна из них. Найдите вероятность того, что она окажется: а) белой; б) желтой; в) не желтой.Задача 5.
Слайд 17Решение
а) Мы имеем всевозможных случаев 9. Благоприятствующих событий 3. Вероятность
равна:
P=3:9=1/3
б) Мы имеем всевозможных случаев 9. Благоприятствующих событий 2. Вероятность
равна P=2:9=2/9в) Мы имеем всевозможных случаев 9. Благоприятствующих событий 7 (4+3). Вероятность равна P=7:9=7/9
Слайд 18Практикум по решению задач.
На четырех карточках написаны буквы О,
Л, Е, Т. Карточки перевернули и перемешали. Затем открыли наугад
последовательно эти карточки и положили в ряд. Какова вероятность того, что получится слово «ЛЕТО»?Решение.
Исходы – все возможные перестановки из четырех элементов (О, Л, Е, Т); общее число исходов:
Событие А - {после открытия карточек получится слово «ЛЕТО»}:
Задача 6.
л
е
о
т
Слайд 19Практикум по решению задач.
Задача 7.
При стрельбе из винтовки
вероятность попадания в цель равна 0,85. Найти вероятное число попаданий,
если всего было произведено 120 выстрелов.Решение.
Слайд 20Использованные источники
Я. Перельман. Занимательная геометрия на вольном воздухе и дома.
- М, 2012.
2. Башмаков, М.И. Математика: учебник для учреждений нач. и
сред. проф. образования / М.И.Башмаков – 8-е изд., стер. - М.: Академия, 2013.-256 c.3. Математика. 10-11 классы: элективный курс «В мире случайных закономерностей» / ав.-сост. В.Н. Студенецкая и др. – Волгоград: Учитель, 2007. – 126 с.
