Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тетраэдр
Содержание
- 1. Тетраэдр
- 2. Понятие ”Тетраэдр” Тетра́эдр — простейший многогранник, гранями которого
- 3. Свойства тетраэдра
- 4. Тетраэдр вокруг насПирамида МаслоуПирамида ХеопсаВ нашей жизни
- 5. Тетраэдр в наукеТетраэдр из грецких ореховНекоторые плоды,
- 6. Симметрия и сечение в кубеЧисло сторон у
- 7. Элементы симметрии кубаСквозь центр симметрии куба проходят
- 8. Сечение в кубе
- 9. ТреугольникПостроить сечение куба плоскостью, проходящей через точки
- 10. ЧетырехугольникПостроить сечение куба плоскостью, проходящей через точки
- 11. Построить сечение куба плоскостью, проходящей через точки
- 12. Скачать презентанцию
Понятие ”Тетраэдр” Тетра́эдр — простейший многогранник, гранями которого являются четыре треугольника. Тетраэдр является треугольной пирамидой при принятии любой из граней за основание. У тетраэдра 4 грани, 4 вершины и 6 рёбер.
Слайды и текст этой презентации
Слайд 2Понятие ”Тетраэдр”
Тетра́эдр — простейший многогранник, гранями которого являются четыре треугольника. Тетраэдр является
Слайд 4Тетраэдр вокруг нас
Пирамида Маслоу
Пирамида Хеопса
В нашей жизни встречается множество разных
предметов бытия и достопримечательностей , в виде разных геометрических фигур.
И такая геометрическая фигура как тетраэдр тому доказательство.
Слайд 5Тетраэдр в науке
Тетраэдр из грецких орехов
Некоторые плоды, находясь вчетвером на
одной кисти, располагаются в вершинах тетраэдра, близкого к правильному. Такая
конструкция обусловлена тем, что центры четырёх одинаковых шаров, касающихся друг друга, находятся в вершинах правильного тетраэдра. Поэтому похожие на шар плоды образуют подобное взаимное расположение. Например, таким образом могут располагаться грецкие орехи.Тетраэдры в технике
Тетраэдр образует жёсткую, статически определимую конструкцию. Тетраэдр, выполненный из стержней, часто используется в качестве основы для пространственных несущих конструкций пролётов зданий, перекрытий, балок, ферм, мостов и т. д. Стержни испытывают только продольные нагрузки.
Прямоугольный тетраэдр используется в оптике. Если грани, имеющие прямой угол, покрыть светоотражающим составом или весь тетраэдр выполнить из материала с сильным светопреломлением, чтобы возникал эффект полного внутреннего отражения, то свет, направленный в грань, противоположную вершине с прямыми углами, будет отражаться в том же направлении, откуда он пришёл. Это свойство используется для создания уголковых отражателей, катафотов.
Граф четверичного триггера представляет собой тетраэдр.
Слайд 6Симметрия и сечение в кубе
Число сторон у грани – 4;
Общее
число граней – 6;
Число рёбер примыкающих к вершине – 3;
Общее
число вершин – 8;Общее число рёбер – 12;
Куб является частным случаем параллелепипеда и призмы. 4 сечения куба имеют вид правильных
шестиугольников — это сечения через центр куба перпендикулярно 4-м главным диагоналям.
В кубе насчитывается шесть квадратов. Все вершины куба являются вершинами 3-х квадратов. То есть,
сумма плоских углов у каждой вершины = 270º.
Слайд 7Элементы симметрии куба
Сквозь центр симметрии куба проходят 9 осей симметрии.
Плоскостей
симметрии у куба тоже 9, они пролегают или
через противолежащие ребра
(таких плоскостей 6), или через середины противолежащих ребер (таких 3).
Слайд 9Треугольник
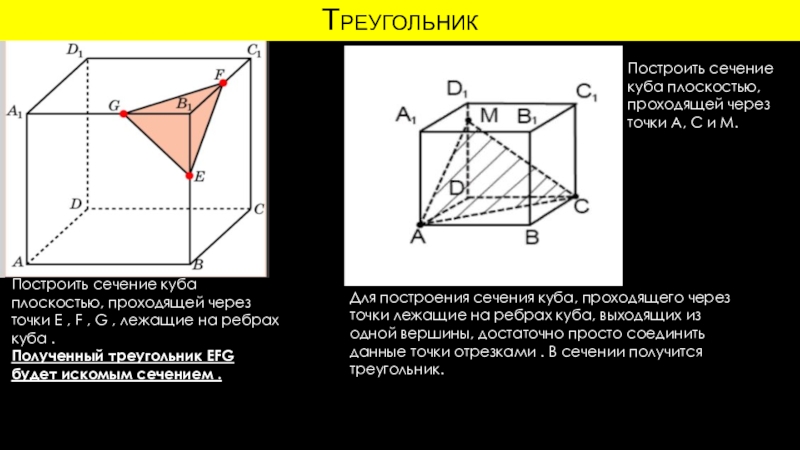
Построить сечение куба плоскостью, проходящей через точки E , F
, G , лежащие на ребрах куба .
Полученный треугольник
EFG будет искомым сечением . Построить сечение куба плоскостью, проходящей через точки A, C и M.
Для построения сечения куба, проходящего через точки лежащие на ребрах куба, выходящих из одной вершины, достаточно просто соединить данные точки отрезками . В сечении получится треугольник.
Слайд 10Четырехугольник
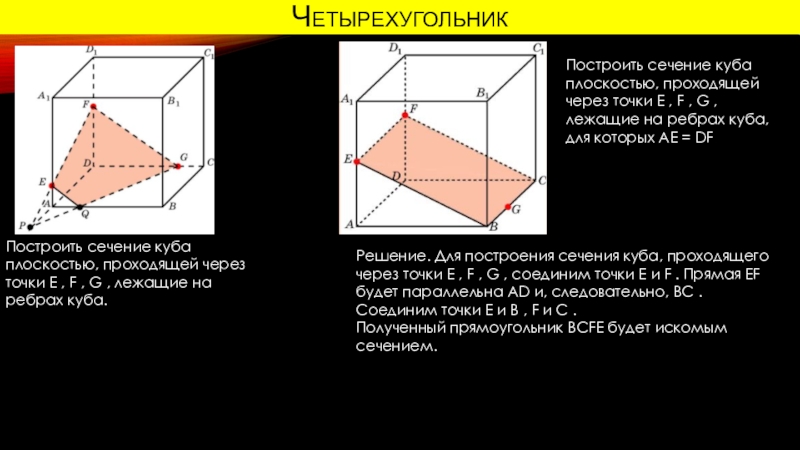
Построить сечение куба плоскостью, проходящей через точки E , F
, G , лежащие на ребрах куба.
Построить сечение куба плоскостью,
проходящей через точки E , F , G , лежащие на ребрах куба, для которых AE = DFРешение. Для построения сечения куба, проходящего через точки E , F , G , соединим точки E и F . Прямая EF будет параллельна AD и, следовательно, BC . Соединим точки E и B , F и C .
Полученный прямоугольник BCFE будет искомым сечением.
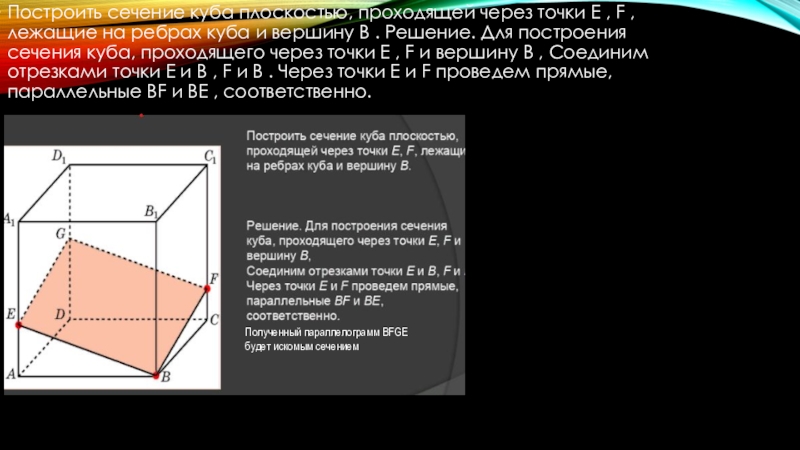
Слайд 11Построить сечение куба плоскостью, проходящей через точки E , F
, лежащие на ребрах куба и вершину B . Решение.
Для построения сечения куба, проходящего через точки E , F и вершину B , Соединим отрезками точки E и B , F и B . Через точки E и F проведем прямые, параллельные BF и BE , соответственно.Полученный параллелограмм BFGE будет искомым сечением
