Тригонометрические функции
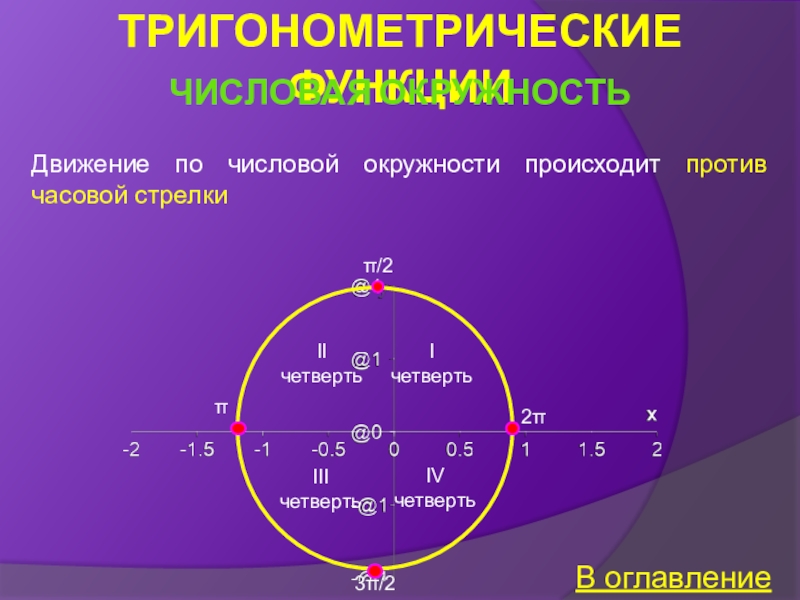
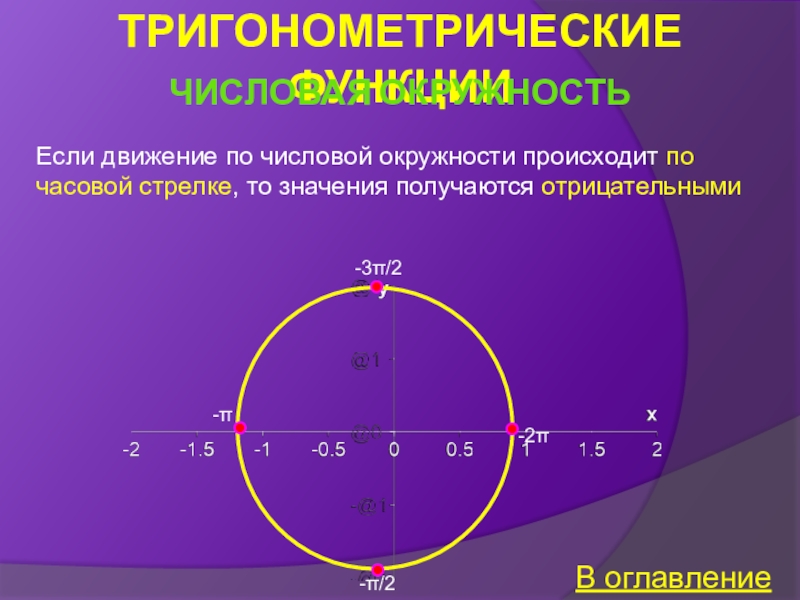
Числовая окружность
Синус и косинус
Тангенс и котангенс
Тригонометрические функции
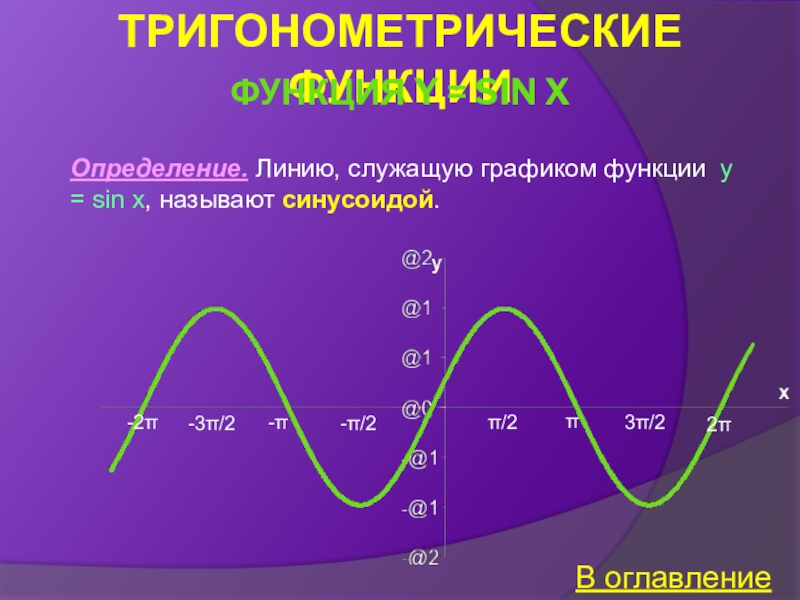
числового аргументаФункция y = sin x
Свойства функции y = sin x
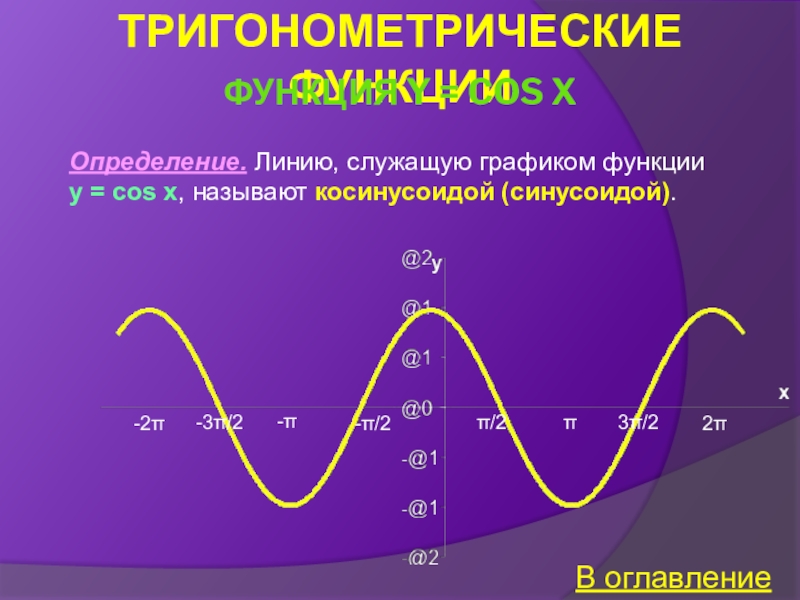
Функция y = cos x
Свойства функции y = cos x
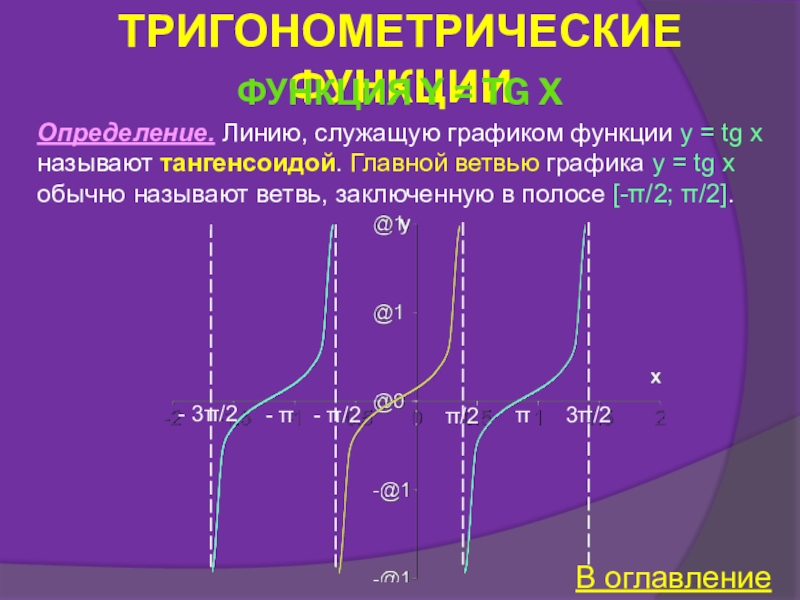
Функция y = tg x
Свойства функции y = tg x
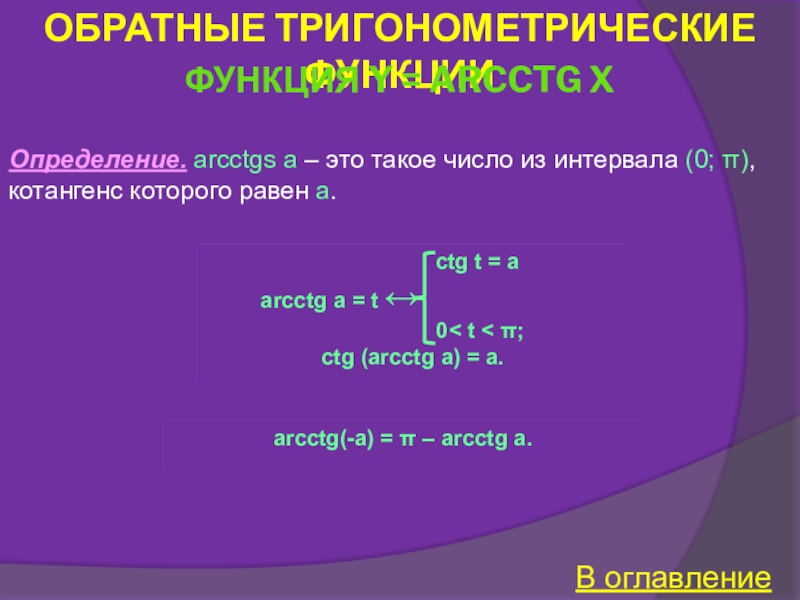
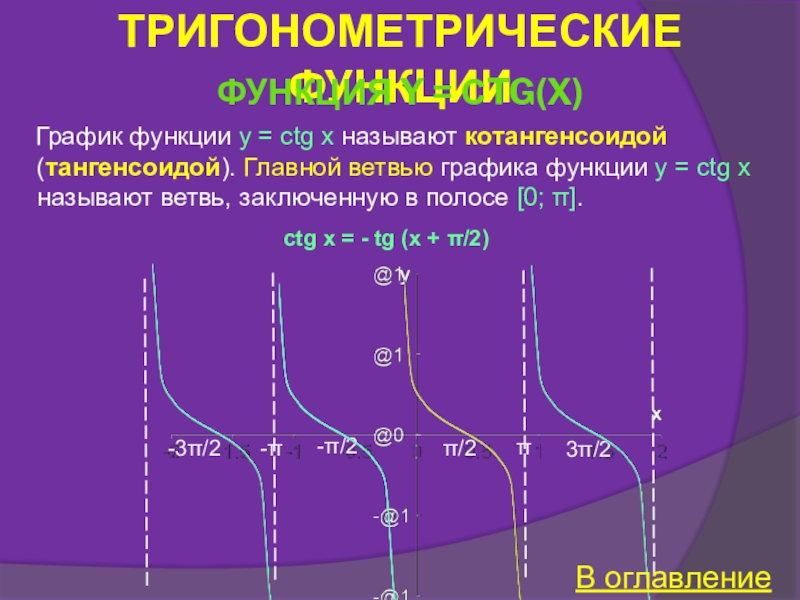
Функция y = ctg x
Свойства функции y = ctg x
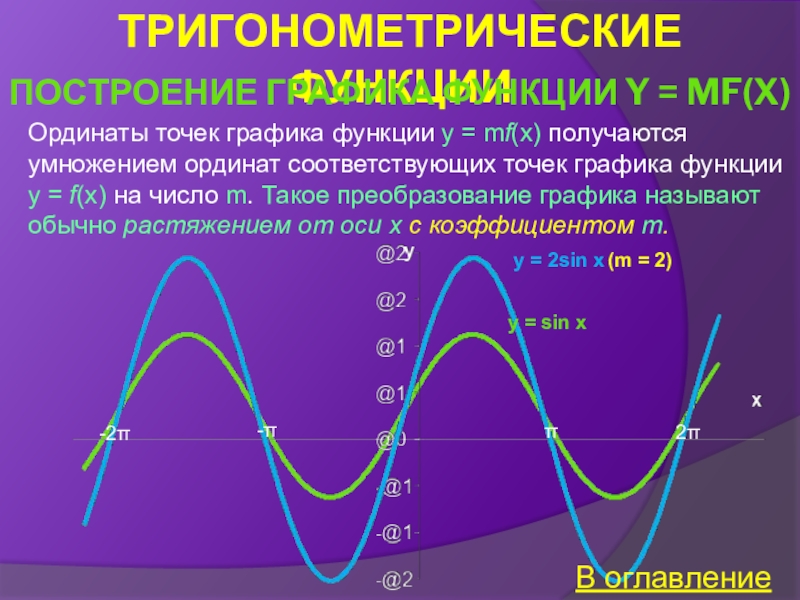
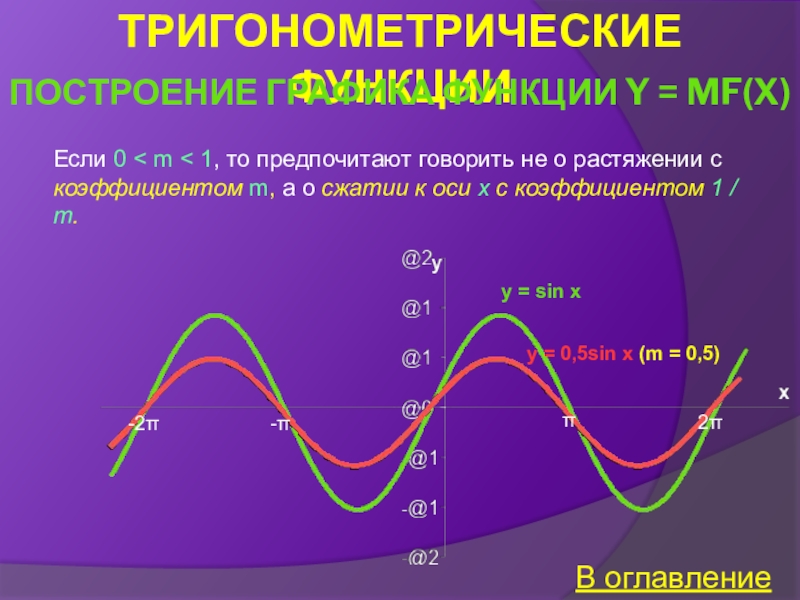
Построение графика функции y = mf(x)
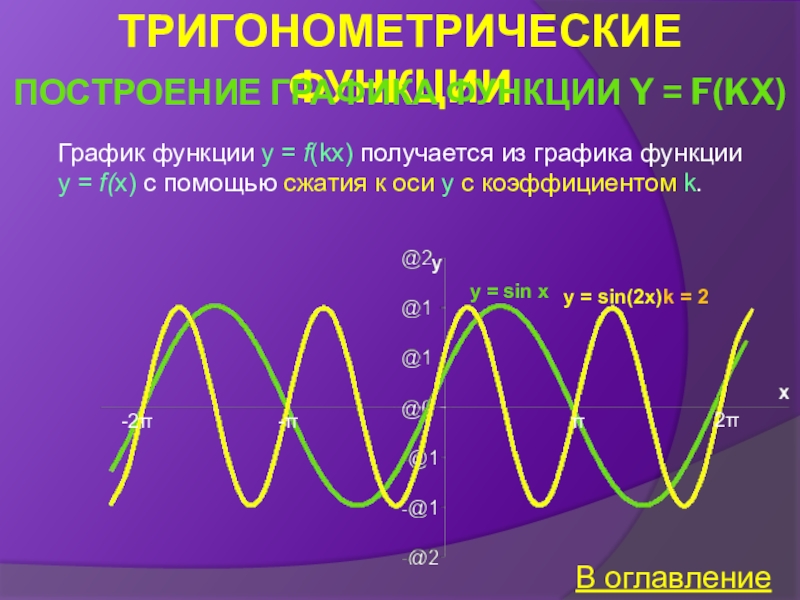
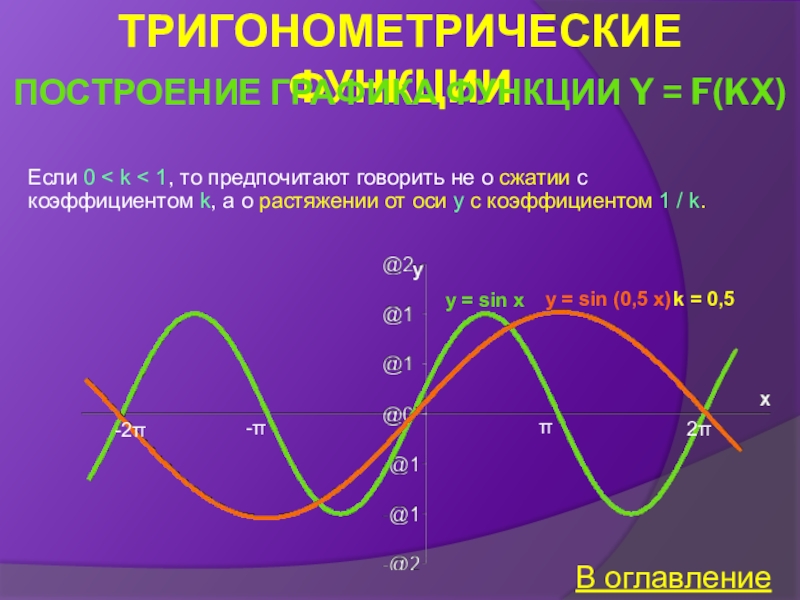
Построение графика функции y = f(kx)
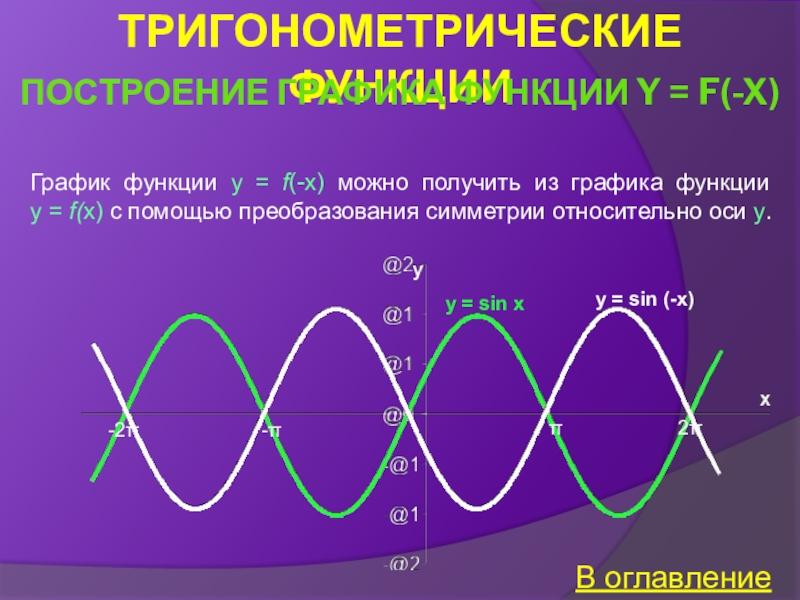
Построение графика функции y = f(-x)
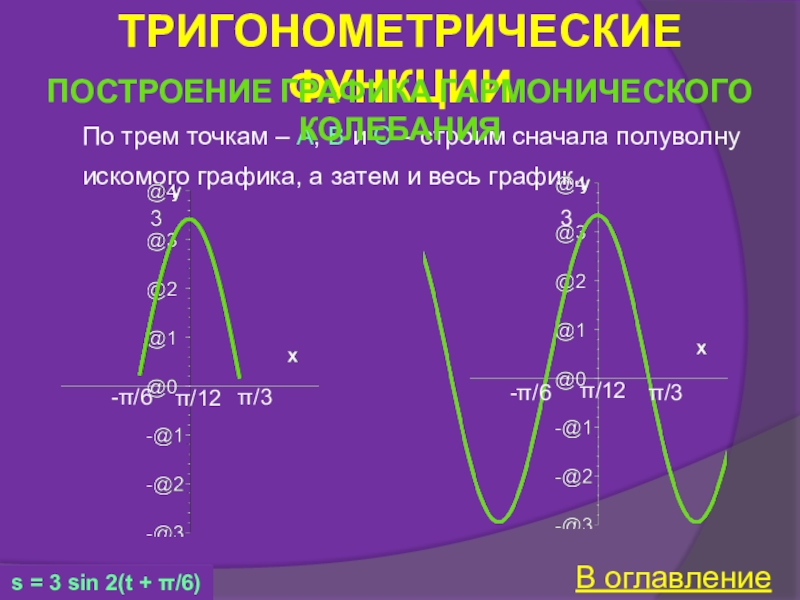
График гармонического колебания
Построение графика гармонического колебания
оглавление


























![ТРИГОНОМЕТРИЧЕСКИЕ
ФУНКЦИИ ЧИСЛОВОГО
АРГУМЕНТА Свойства функции y = arcsin x. Свойство 1. D(f) Свойства функции y = arcsin x. Свойство 1. D(f) = [-1;1].Свойство 2.](/img/tmb/7/628804/b0b8698ad6e011e5630960a4e8cddf70-800x.jpg)
![ТРИГОНОМЕТРИЧЕСКИЕ
ФУНКЦИИ ЧИСЛОВОГО
АРГУМЕНТА Определение. Если |a| ≤ 1, то arcsin a – это Определение. Если |a| ≤ 1, то arcsin a – это такое число из отрезка [-π/2; π/2],](/img/tmb/7/628804/9df7bb86b807e381e838fe051d4c8257-800x.jpg)

![ТРИГОНОМЕТРИЧЕСКИЕ
ФУНКЦИИ ЧИСЛОВОГО
АРГУМЕНТА Свойства функции y = arccos x. Свойство 1. D(f) Свойства функции y = arccos x. Свойство 1. D(f) = [-1;1].Свойство 2.](/img/tmb/7/628804/b2273e06da4b8b506bed6ba4c7a71c42-800x.jpg)
![ТРИГОНОМЕТРИЧЕСКИЕ
ФУНКЦИИ ЧИСЛОВОГО
АРГУМЕНТА Определение. Если |a| ≤ 1, то arccos a – это Определение. Если |a| ≤ 1, то arccos a – это такое число из отрезка [0; π],](/img/tmb/7/628804/4e44ca3e3eb96d3463478a8a215b2e02-800x.jpg)
![ТРИГОНОМЕТРИЧЕСКИЕ
ФУНКЦИИ ЧИСЛОВОГО
АРГУМЕНТА Теорема. Для любого a є [-1; 1] выполняется равенство arccos Теорема. Для любого a є [-1; 1] выполняется равенство arccos a + arccos (-a) = π.Обратные](/img/tmb/7/628804/34d070b7db007bf4bf22864132ff6a30-800x.jpg)