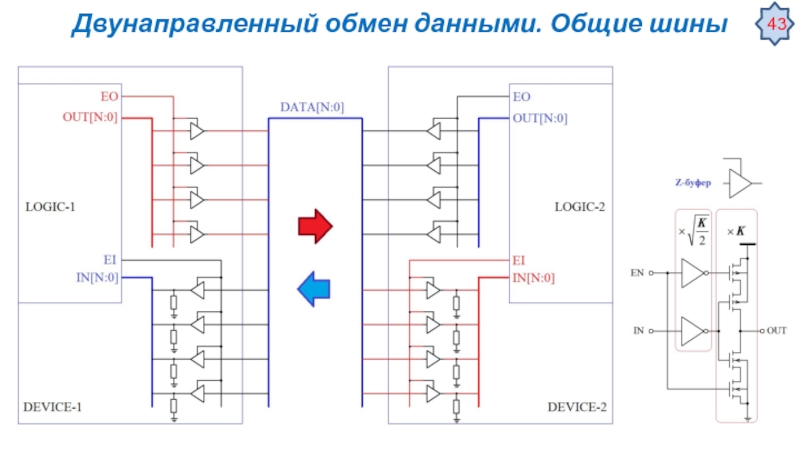
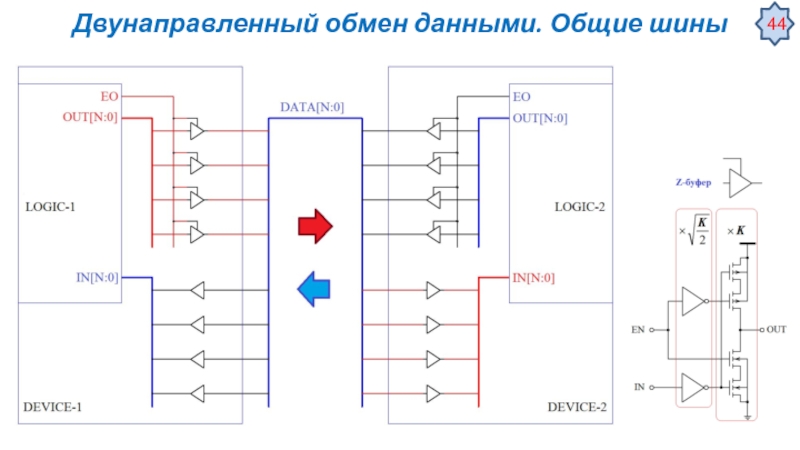
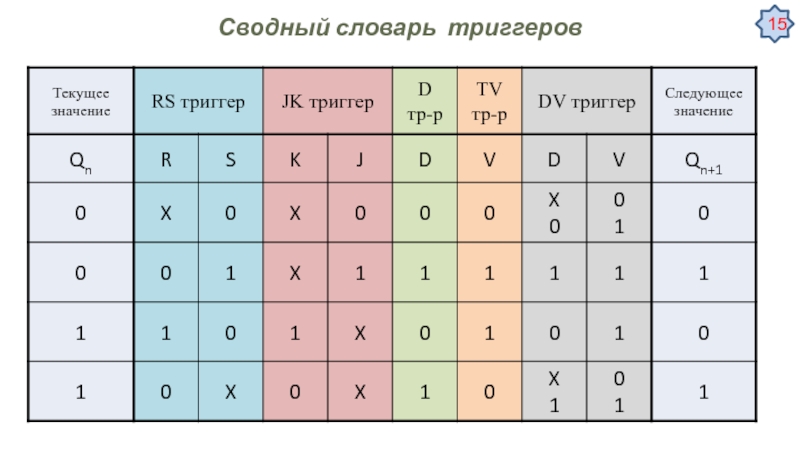
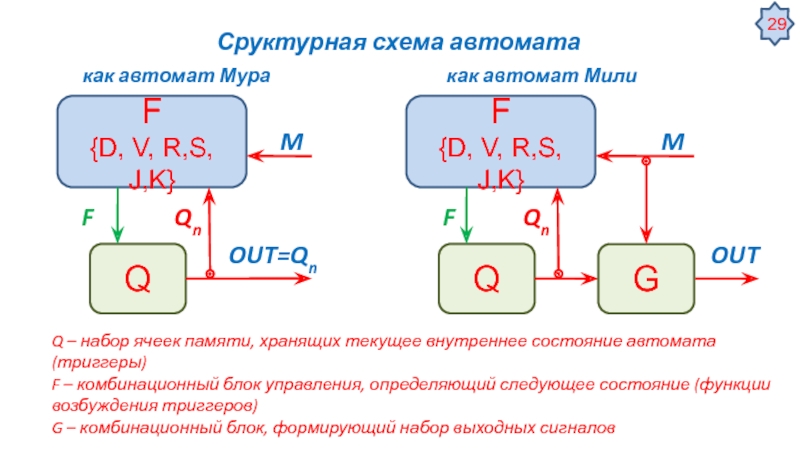
Автомат описывается набором множеств:
A = {a1 … aN} — множество
значений состояний устройстваZ = {z1 … zN} — множество значений входных управляющих сигналов
W = {w1 … wN}— множество значений выходных сигналов
δ — функция переходов от текущего состояния аn в следующее состояние an+1
λ — функция зависимости выходов от значений аn и zn
а1 — начальное состояние автомата
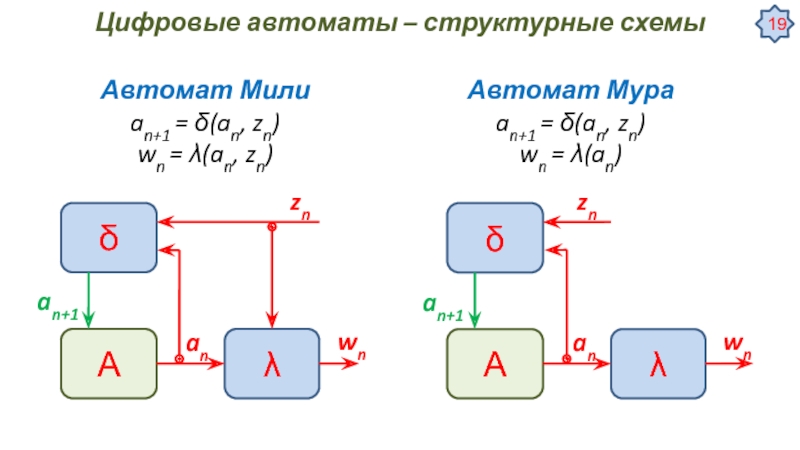
Автомат Мили
an+1 = δ(an, zn)
wn = λ(an, zn)
Автомат Мура
an+1 = δ(an, zn)
wn = λ(an)

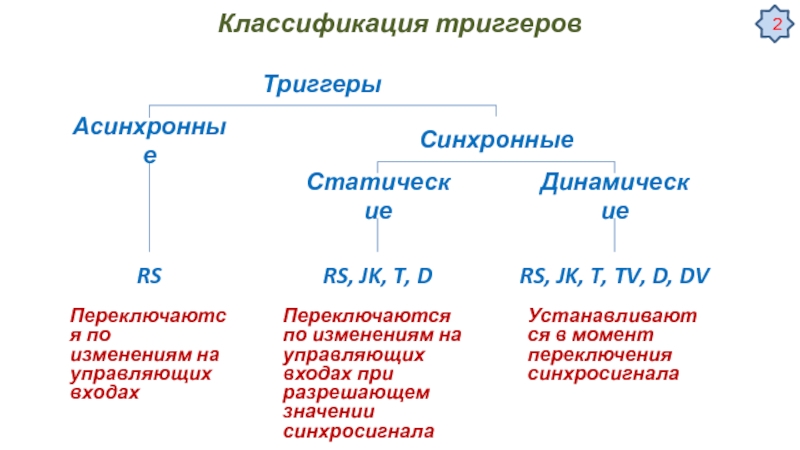
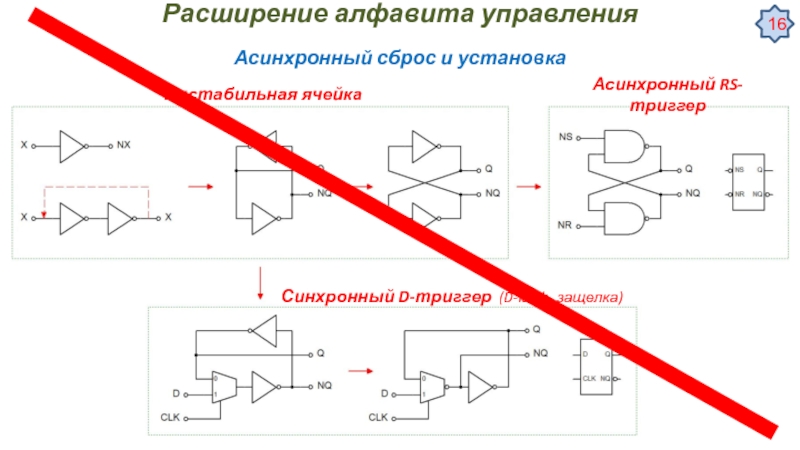
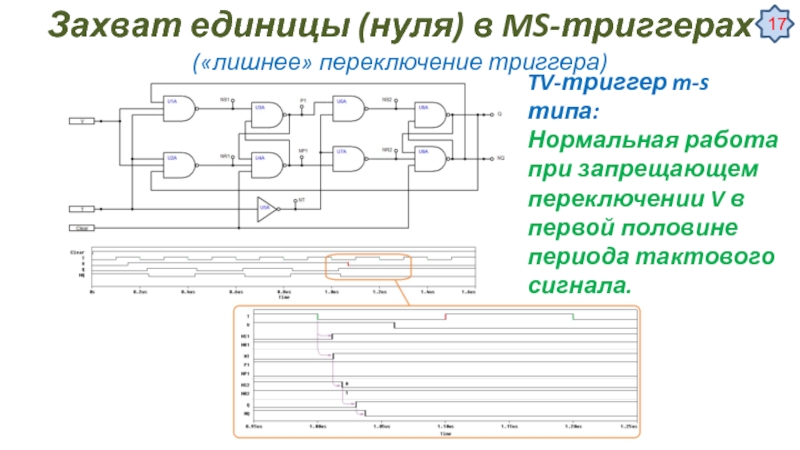
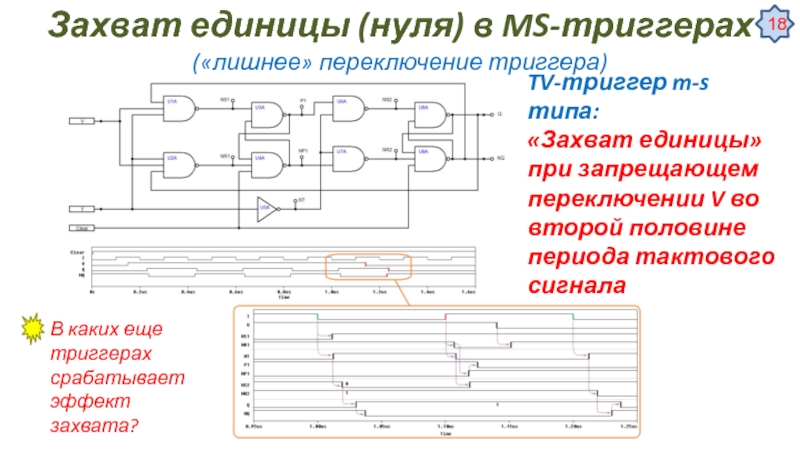
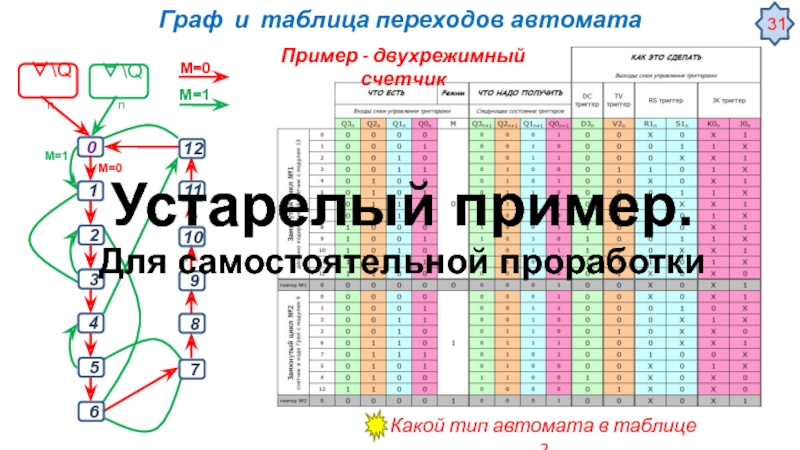
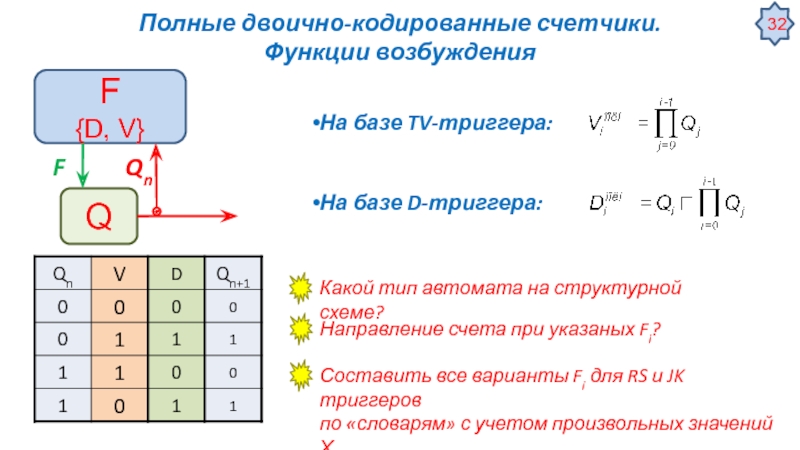
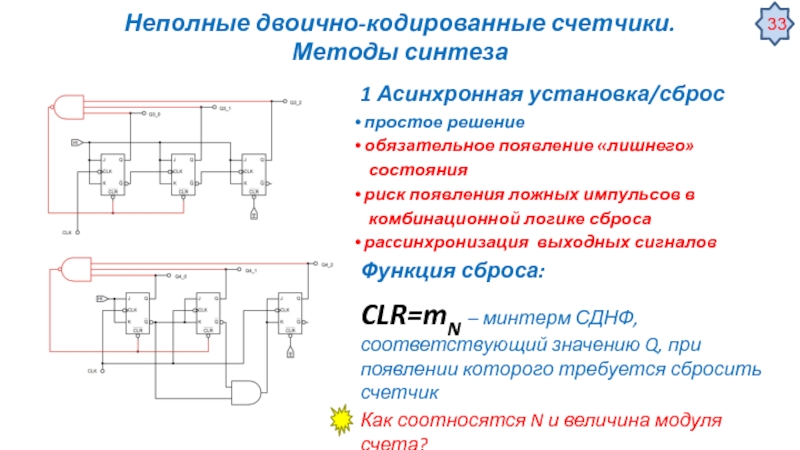
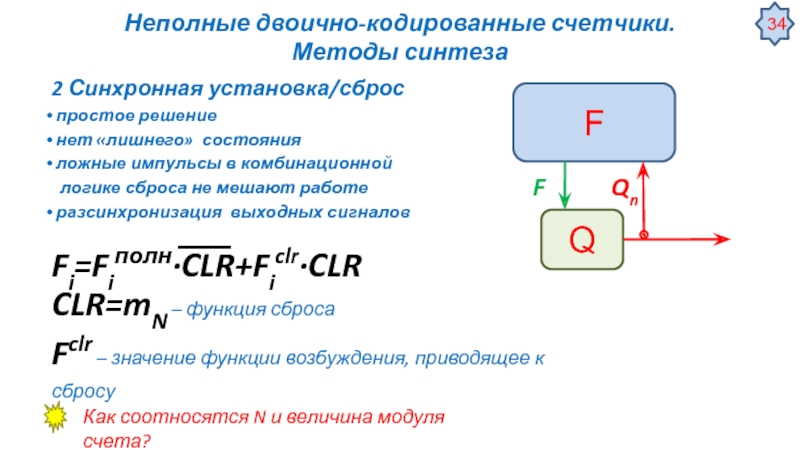

![Цифровые автоматы – общие сведения Некоторые специальные применения триггеровУстранение дребезга контактов механических переключателей [Ульрих Титце, Кристоф Некоторые специальные применения триггеровУстранение дребезга контактов механических переключателей [Ульрих Титце, Кристоф Шенк, Полупроводниковая схемотехника, том I]](/img/tmb/3/276034/81a66e88d716c75611f128f261d3c14f-800x.jpg)