Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Учебная дисциплина Схемотехника дискретных устройств Тема: Арифметические и
Содержание
- 1. Учебная дисциплина Схемотехника дискретных устройств Тема: Арифметические и
- 2. Тема: Арифметические и логические основы ЭВМ
- 3. ВысказываниеОсновное понятие алгебры логики-высказывание.Простое Высказывание - некоторое
- 4. Высказывание Сложным высказыванием является предложение, состоящее из
- 5. Высказывание Под логическими связями понимаются грамматические союзы типа «НЕ», «И», «ИЛИ», «ЕСЛИ.., ТО..».
- 6. Высказывание Любое высказывание можно обозначить символом х
- 7. ВысказываниеВысказывание абсолютно истинно, если соответствующая ему логическая
- 8. Определение булевой функции Под булевой функцией (БФ)
- 9. Определение булевой функции Простые высказывания, входящие в
- 10. Определение булевой функцииЧтобы задать булеву функцию надо
- 11. Определение булевой функции Количество возможных булевых функций N при количестве переменных p, определяется по формуле:
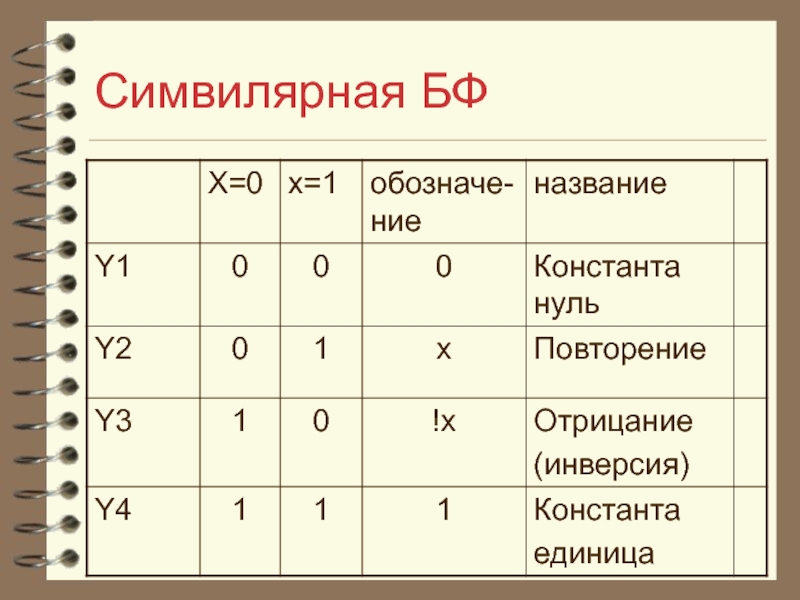
- 12. Симвилярная БФ БФ одной переменной называется симвилярной функцией.
- 13. Симвилярная БФ
- 14. Бинарная булева функция Булева функция от двух переменных называется бинарной.
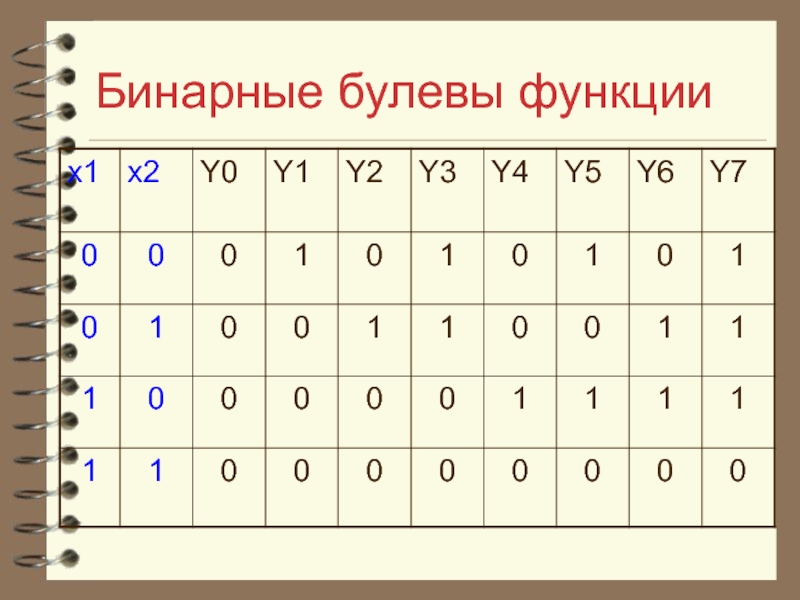
- 15. Бинарные булевы функции
- 16. Бинарные булевы функции
- 17. Наименования бинарных булевых функций Y0- константа 0
- 18. Наименования бинарных булевых функцийY7 – функция Шеффера
- 19. Наименования бинарных булевых функцийY12 – переменная x1
- 20. Определение логической функцииЛогическая функция алгебры логики –
- 21. Применимость алгебры логики Возможность применения алгебры
- 22. Технический аналог булевой функции Техническим аналогом
- 23. Понятие логического элемента Логические операции над двоичными
- 24. Законы и аксиомы алгебры логики Закон одинарных
- 25. Законы и аксиомы алгебры логики Закон двойственности Де Моргана
- 26. Законы и аксиомы алгебры логикиИз этих выражений следует следствие:
- 27. Комбинационные законыЗакон тавтологии:Х+Х+Х+…….+Х=ХХ*Х*Х*……*Х=ХПереместительный (коммутативный) закон:Х1+Х2=Х2+Х1 Х1*Х2=Х2*Х1
- 28. Комбинационные законыСочетательный (ассоциативный) закон:(Х1+Х2)+Х3=Х1+(Х2+Х3)(Х1*Х2)*Х3=Х1*(Х2*Х3)
- 29. Комбинационные законы Распределительный закон:X1*(X2+X3)=(X1*X2)+(X1*X3)X1+(X2*X3)=(X1+X2)*(X1+X3)
- 30. Комбинационные законы Сочетательный закон: X1*(X2*X3)=(X1*X3)*X2 X1+(X2+X3)=(X1+X2)+X3
- 31. Комбинационные законы Переместительный закон(закон коммутативности): X1*X2*X3=X3*X2*X1 X1+X2+X3=X3+X1+X2
- 32. Комбинационные законы Закон поглощения (абсорбции): X1+X1*X2=X1 X1*(X1+X2)=X1
- 33. Комбинационные законы Закон склеивания:
- 34. Теорема ШеннонаОперация инвертирования произвольной комбинации двоичных переменных,
- 35. Теорема Шеннона (продолжение) исходных значений двоичных переменных
- 36. Пример применения теоремы Шеннона
- 37. Определение Основного Функционально полного набораНабор функций дизъюнкции,
- 38. Другие функционально полные наборы Двумя другими функционально полными наборами являются функции Пирса и Шеффера.
- 39. Функционально полная система логических элементов Систему логических
- 40. Понятие « базис» Система переключательных функций , образующую функционально полную систему, логических функций называется базисом.
- 41. Переключательная функция Переключательной функцией называется математическое выражение,
- 42. Дизъюнктивно-нормальная форма (ДНФ) Если логическая функция
- 43. Элементарная конъюнкция Элементарной конъюнкцией n-го ранга называется
- 44. Ранг конъюнкции Рангом конъюнкции называется число
- 45. Конъюнктивно-нормальная форма (КНФ)Если логическая функция выражена посредством
- 46. Элементарная дизъюнкцияЭлементарной дизъюнкцией n-го ранга называется логическая
- 47. Ранг дизъюнкции Рангом дизъюнкции называется число двоичных
- 48. Эквивалентность представления Одна и та же логическая
- 49. СДНФ Совершенная дизъюнктивно-нормальная форма логической функции от
- 50. СДНФ - нет двух одинаковых конъюнкций; -
- 51. Определение минтерма Конъюнкции n-го ранга, составляющие СДНФ
- 52. СКНФ Совершенная конъюнктивно-нормальная форма логической функции от
- 53. СКНФ- нет двух одинаковых дизъюнкций; - каждая
- 54. Определение минтермаДизъюнкции n-го ранга, составляющие СКНФ функции
- 55. Примеры СКНФ и СДНФСДНФ:СКНФ:
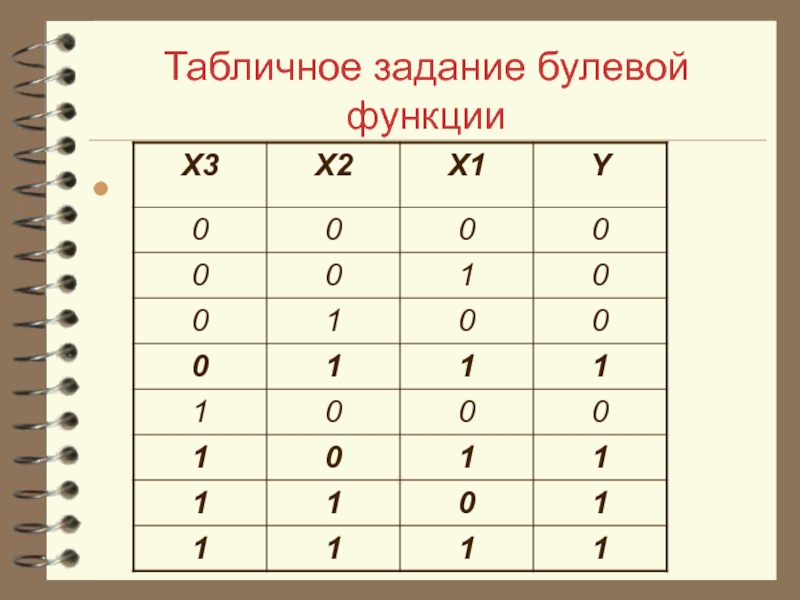
- 56. Табличное задание булевой функции
- 57. Составление СДНФ по табличному заданию булевой функции
- 58. Итоговая запись СДНФ
- 59. Составление СКНФ по табличному заданию булевой функцииПравило:Соответствующие
- 60. Итоговая запись СКНФ
- 61. Технический аналог булевой функцииТехническим аналогом булевой функции
- 62. Типовой порядок проектирования комбинационных устройств Этапы:1. Определение
- 63. Типовой порядок проектирования комбинационных устройств5. Составление комбинационной схемы из логических элементов, входящих в указанный базис.
- 64. Минимизация логических функций. Упрощение и преобразование логических
- 65. Минимизация логических функций. Различают эвристические и формализованные
- 66. Принципы минимизации Основным методом минимизации логических функций,
- 67. Принципы минимизацииглавной задачей при минимизации СДНФ и
- 68. Метод Карт Карно При формализованных методах, при
- 69. Карты КарноКарты Карно были изобретены в 1952
- 70. Правило составления карты КарноВ карту Карно булевы
- 71. Пример карты Карно для 4-х переменных
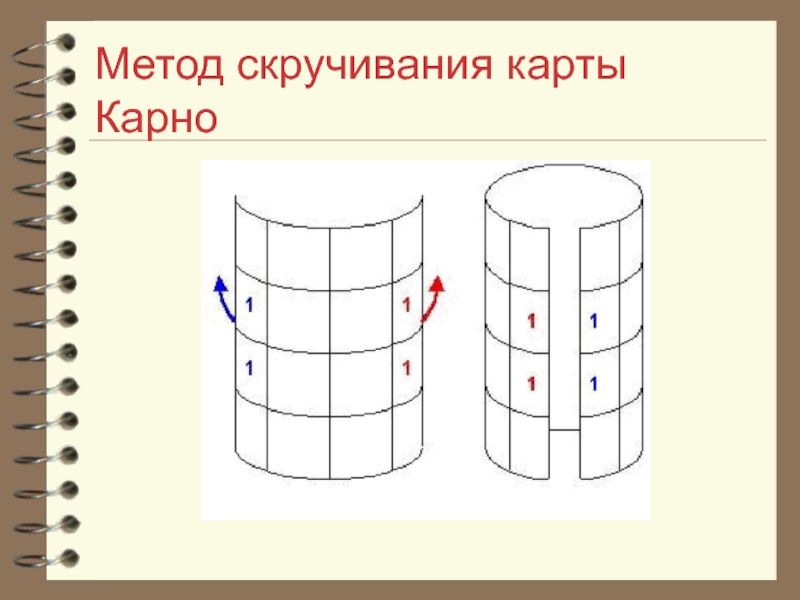
- 72. Метод скручивания карты Карно Крайние квадраты карты
- 73. Метод скручивания карты Карно
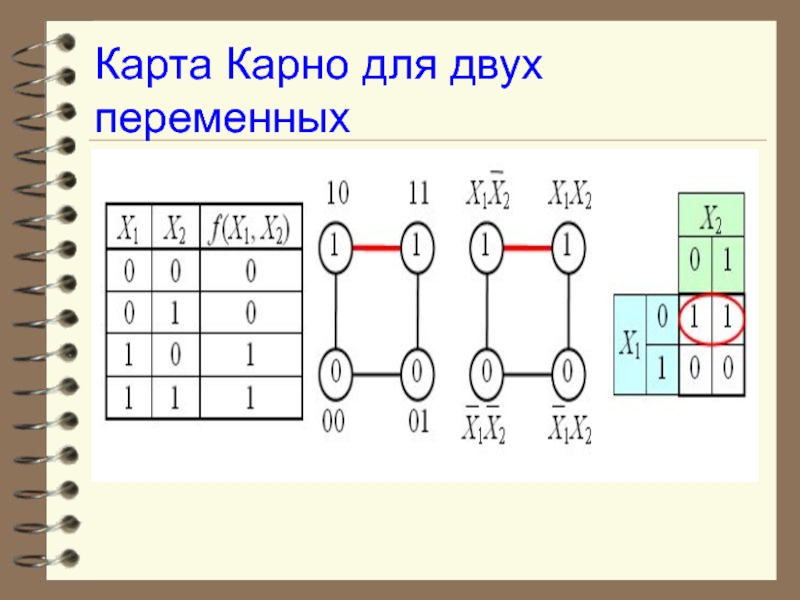
- 74. Карта Карно для двух переменных
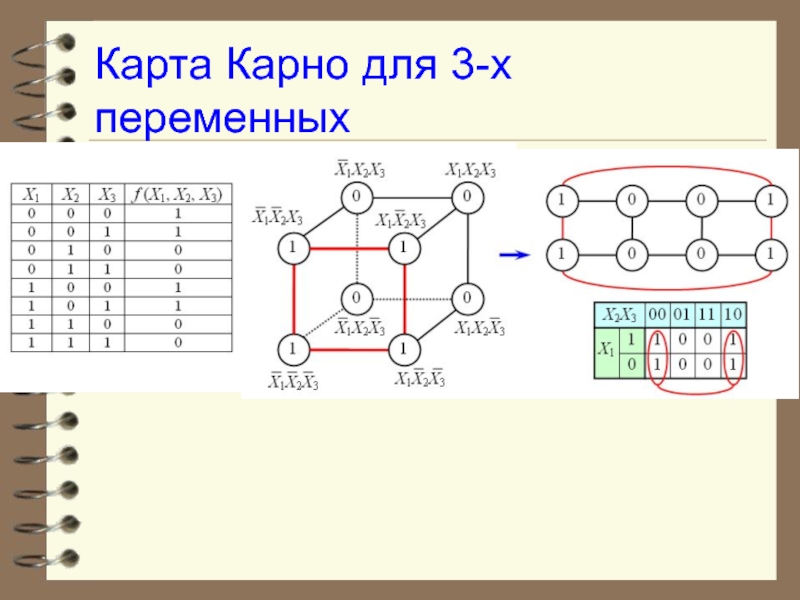
- 75. Карта Карно для 3-х переменных
- 76. Скачать презентанцию
Тема: Арифметические и логические основы ЭВМ Логика- наука о формах и законах мышления (в общем понимании)Математическая логика- наука о применении математических методов для решения различного рода логических задач.
Слайды и текст этой презентации
Слайд 2Тема: Арифметические и логические основы ЭВМ
Логика- наука о
формах и законах мышления (в общем понимании)
Математическая логика- наука о
применении математических методов для решения различного рода логических задач.
Слайд 3Высказывание
Основное понятие алгебры логики-высказывание.
Простое Высказывание - некоторое предложение, о котором
можно утверждать, что оно истинно или ложно.
Слайд 4Высказывание
Сложным высказыванием является предложение, состоящее из нескольких простых предложений
(т.е. простых высказываний), связанных между собой какими либо логическими связями.
Слайд 5Высказывание
Под логическими связями понимаются грамматические союзы типа «НЕ», «И»,
«ИЛИ», «ЕСЛИ.., ТО..».
Слайд 6Высказывание
Любое высказывание можно обозначить символом х и считать, что
х=1, если высказывание истинно, а х=0, если высказывание ложно.
Логическая (булева)
переменная – такая величина х, которая может принимать только два значения: х={0,1}.
Слайд 7Высказывание
Высказывание абсолютно истинно, если соответствующая ему логическая величина принимает значение
х=1 при любых условиях.
Высказывание абсолютно ложно, если соответствующая ему логическая
величина принимает значение х=0 при любых условиях.
Слайд 8Определение булевой функции
Под булевой функцией (БФ) понимают сложное высказывание.
Эта
функция принимает лишь два значения: 0 или 1. Булева функция
всегда конечна.
Слайд 9Определение булевой функции
Простые высказывания, входящие в булеву функцию, называют
переменными (или булевыми переменными).
Булева (двоичная) функция – это двоичная
переменная Y, значение которой зависит от её двоичных переменных (аргументов функции).
Слайд 10Определение булевой функции
Чтобы задать булеву функцию надо каждому из возможных
сочетаний аргументов x1,x2,…,xn поставить в соответствие 0 или 1 (т.е.
значение функции).
Слайд 11Определение булевой функции
Количество возможных булевых функций N при количестве
переменных p, определяется по формуле:
Слайд 17Наименования бинарных булевых функций
Y0- константа 0
Y0=0
Y1 – функция Пирса
Y1=!(x1+x2)Y2 – запрет по x1 Y2=!x1*x2
Y3 – переменная !x1 Y3=!x1
Y4 – запрет по x2 Y4=x1*!x2
Y5 – переменная !x2 Y5=!x2
Y6 – искл. ИЛИ (сложение по модулю 2)
Слайд 18Наименования бинарных булевых функций
Y7 – функция Шеффера Y7=!(x1*x2)
Y8 – конъюнкция
Y8=x1*x2
Y9 – равнозначность
Y9=x1=x2Y10- перемен. x2 Y10=x2
Y11- импликация x1 x2
Y11=!x1+x2
Слайд 19Наименования бинарных булевых функций
Y12 – переменная x1
Y12=x1
Y13 – импликация x2 к x1
Y13=x1+!x2Y14 – дизъюнкция Y14=x1+x2
Y15 – константа единицы Y15=1
Слайд 20Определение логической функции
Логическая функция алгебры логики – функция f(x1, x2,
…., xn), принимающая значение, равное 0 или 1 на наборе
логических переменных х1, х2, …..хn.
Слайд 21Применимость алгебры логики
Возможность применения алгебры логики к задачам
проектирования вычислительных устройств обусловлена аналогией понятий и категорий алгебры логики
и двоичной системы счисления.
Слайд 22Технический аналог булевой функции
Техническим аналогом булевой функции является
комбинационная схема, выполняющая соответствующее этой функции преобразование информации.
Постоянные уровни напряжения,
соответствующие принятому в схеме представлению 0 и 1, могут рассматриваться как технические аналоги функции «ложь» и «истина». 
Слайд 23Понятие логического элемента
Логические операции над двоичными переменными реализуются схемами,
которые называются логическими элементами.
Число входов логического элемента соответствует числу
аргументов воспроизводимой им булевой функции.
Слайд 24Законы и аксиомы алгебры логики
Закон одинарных элементов:
Х+1=1 Х*1=Х
Х+0=Х Х*0=0
Законы
отрицания:- закон двойного отрицания
- закон дополнительности
Слайд 27Комбинационные законы
Закон тавтологии:
Х+Х+Х+…….+Х=Х
Х*Х*Х*……*Х=Х
Переместительный (коммутативный) закон:
Х1+Х2=Х2+Х1 Х1*Х2=Х2*Х1
Слайд 28Комбинационные законы
Сочетательный (ассоциативный) закон:
(Х1+Х2)+Х3=Х1+(Х2+Х3)
(Х1*Х2)*Х3=Х1*(Х2*Х3)
Слайд 29Комбинационные законы
Распределительный закон:
X1*(X2+X3)=(X1*X2)+(X1*X3)
X1+(X2*X3)=(X1+X2)*(X1+X3)
Слайд 31Комбинационные законы
Переместительный закон
(закон коммутативности):
X1*X2*X3=X3*X2*X1
X1+X2+X3=X3+X1+X2
Слайд 34Теорема Шеннона
Операция инвертирования произвольной комбинации двоичных переменных, связанных знаками дизъюнкции
и конъюнкции эквивалентна замене в этой комбинации
Слайд 35Теорема Шеннона (продолжение)
исходных значений двоичных переменных их инверсными значениями
при одновременной замене знаков дизъюнкции и конъюнкции.
Слайд 37Определение Основного Функционально полного набора
Набор функций дизъюнкции, конъюнкции и инверсии,
который соответствует трём операциям булевой алгебры-логики, получил название Основного функционально-полного
набора.
Слайд 38Другие функционально полные наборы
Двумя другими функционально полными наборами являются
функции Пирса и Шеффера.
Слайд 39Функционально полная система логических элементов
Систему логических элементов называют функционально
полной, если есть возможность создать любые заданные переключательные выходные функции.
Слайд 40Понятие « базис»
Система переключательных функций , образующую функционально полную
систему, логических функций называется базисом.
Слайд 41Переключательная функция
Переключательной функцией называется математическое выражение, связывающее между собой
элементарные двоичные логические переменные, принимающие значения «0» и «1».
Слайд 42Дизъюнктивно-нормальная форма (ДНФ)
Если логическая функция выражена посредством логической
суммы элементарных конъюнкций, то считается, что она задана своей ДНФ.
Y=A*B+C*D=(A^B)v(C^D)
Слайд 43Элементарная конъюнкция
Элементарной конъюнкцией n-го ранга называется логическое произведение двоичных
переменных и их отрицаний, причём, каждая переменная в произведении должна
встречаться только один раз. Например:X1^X2^!X3^X4^!X5
Слайд 44Ранг конъюнкции
Рангом конъюнкции называется число двоичных переменных, составляющих
элементарную конъюнкцию.
Например : X1^X2^!X3^X4^!X5; - это конъюнкция 5-го ранга,
так как составлена из произведения пяти переменных и их отрицаний.
Слайд 45Конъюнктивно-нормальная форма (КНФ)
Если логическая функция выражена посредством логического произведения элементарных
дизъюнкций, то считается, что она задана своей КНФ.
Y=(A+B)*(C+D)=(AvB)^(CvD)
Слайд 46Элементарная дизъюнкция
Элементарной дизъюнкцией n-го ранга называется логическая сумма двоичных переменных
и их отрицаний, причём, каждая переменная в сумме должна встречаться
только один раз. Например:X1vX2v!X3vX4v!X5
Слайд 47Ранг дизъюнкции
Рангом дизъюнкции называется число двоичных переменных, составляющих элементарную
дизъюнкцию.
Например : X1vX2v!X3vX4v!X5; - это дизъюнкция 5-го ранга, так как
составлена из логической суммы пяти переменных и их отрицаний.
Слайд 48Эквивалентность представления
Одна и та же логическая функция может быть
представлена как своей ДНФ так и КНФ, путём эквивалентных преобразований.
Из множества этих нормальных форм функций выделяют одну совершенную дизъюнктивную (СДНФ) и одну совершенную конъюнктивную (СКНФ) формы. 
Слайд 49СДНФ
Совершенная дизъюнктивно-нормальная форма логической функции от n двоичных переменных
называется такая ДНФ логической функции в которой:
- все конъюнкции
имеют один и тот же ранг;
Слайд 50СДНФ
- нет двух одинаковых конъюнкций;
- каждая конъюнкция содержит
либо прямое, либо инверсное значение двоичной переменной;
- ни одна
конъюнкция не содержит двух одинаковых двоичных переменных.
Слайд 51Определение минтерма
Конъюнкции n-го ранга, составляющие СДНФ функции и обращающие
функцию в 1 при определённом наборе переменных получили название минтермы.
Слайд 52СКНФ
Совершенная конъюнктивно-нормальная форма логической функции от n двоичных переменных
называется такая КНФ логической функции в которой:
- все дизъюнкции
имеют один и тот же ранг;
Слайд 53СКНФ
- нет двух одинаковых дизъюнкций;
- каждая дизъюнкция содержит либо
прямое, либо инверсное значение двоичной переменной;
- ни одна дизъюнкция
не содержит двух одинаковых двоичных переменных.
Слайд 54Определение минтерма
Дизъюнкции n-го ранга, составляющие СКНФ функции и обращающие функцию
в 0 при определённом наборе переменных получили название минтермы.
Слайд 57Составление СДНФ по табличному заданию булевой функции
Правило:
Соответствующие минтермам элементарные
конъюнкции объединить знаками дизъюнкций,
в элементарных конъюнкциях переменная=1 записывается прямым
значением, а переменная=0, своим инверсным значением (с черточкой над именем переменной).
Слайд 59Составление СКНФ по табличному заданию булевой функции
Правило:
Соответствующие минтермам элементарные дизъюнкции
объединить знаками конъюнкций,
в элементарных дизъюнкциях переменная=0 записывается прямым значением,
а переменная=1, своим инверсным значением (с черточкой над именем переменной).
Слайд 61Технический аналог булевой функции
Техническим аналогом булевой функции является комбинационная схема,
выполняющая соответствующее этой функции преобразование информации.
Постоянные уровни напряжения, соответствующие принятому
в схеме представлению 0 и 1, могут рассматриваться как технические аналоги функции «ложь» и «истина». 
Слайд 62Типовой порядок проектирования комбинационных устройств
Этапы:
1. Определение табличных значений поведения
булевой функции.
2. Составление СДНФ по минтермам табличной записи булевой функции.
3.
Упрощение СДНФ и получение его минимальной ДНФ.4. Переход от минимальной ДНФ к минимизированной форме в каком-либо базисе ФПН.
Слайд 63Типовой порядок проектирования комбинационных устройств
5. Составление комбинационной схемы из логических
элементов, входящих в указанный базис.
Слайд 64Минимизация логических функций.
Упрощение и преобразование логических функций имеет целью
получение такого вида функции, при котором построенная в соответствии с
ней цифровая комбинационная схема отличалась бы минимальным расходом логических элементов на её изготовление.
Слайд 65Минимизация логических функций.
Различают эвристические и формализованные методы преобразования логических
функций.
При эвристических методах преобразования логических функций используют законы, аксиомы
и тождества алгебры логики.
Слайд 66Принципы минимизации
Основным методом минимизации логических функций, представленных в виде
СДНФ или СКНФ является операция попарного неполного склеивания и элементарного
поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке.
Слайд 67Принципы минимизации
главной задачей при минимизации СДНФ и СКНФ является поиск
термов, пригодных к склейке с последующим поглощением, что для больших
форм может оказаться достаточно сложной задачей. Карты Карно предоставляют наглядный способ отыскания таких термов.Как известно, булевы функции N переменных, представленные в виде СДНФ или СКНФ могут иметь в своём составе 2N различных термов. Все эти члены составляют некоторую структуру, топологически эквивалентную N–мерному кубу, причём любые два терма, соединённые ребром, пригодны для склейки и поглощения.
На рисунке изображена простая таблица истинности для функции из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов:
Слайд 68Метод Карт Карно
При формализованных методах, при ограничении числа переменных
до пяти-шести используется «метод Карт Карно».
Карта Карно́ — графический способ
минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями. 
Слайд 69Карты Карно
Карты Карно были изобретены в 1952 Эдвардом В. Вейчем
и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs»,
и были призваны помочь упростить цифровые электронные схемы.
Слайд 70Правило составления карты Карно
В карту Карно булевы переменные передаются из
таблицы истинности и упорядочиваются с помощью кода Грея, в котором
каждое следующее число отличается от предыдущего только одним разрядом.
Слайд 72Метод скручивания карты Карно
Крайние квадраты карты являются соседними при
ее скручивании. Это значит, что они тоже подлежат минимизации. На
плоскости можно изобразить карту Карно для 4-х переменных. Для 5 и более переменных необходимы объемные фигуры.
