Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Учебный курс Системы коммутации-1
Содержание
- 1. Учебный курс Системы коммутации-1
- 2. Основная литератураЛ1. Гольдштейн Б.С. Системы коммутации. Учебник
- 3. Изложение этого материала в:[Л1]. Параграф 1.7[Л2]. Параграф 2.3
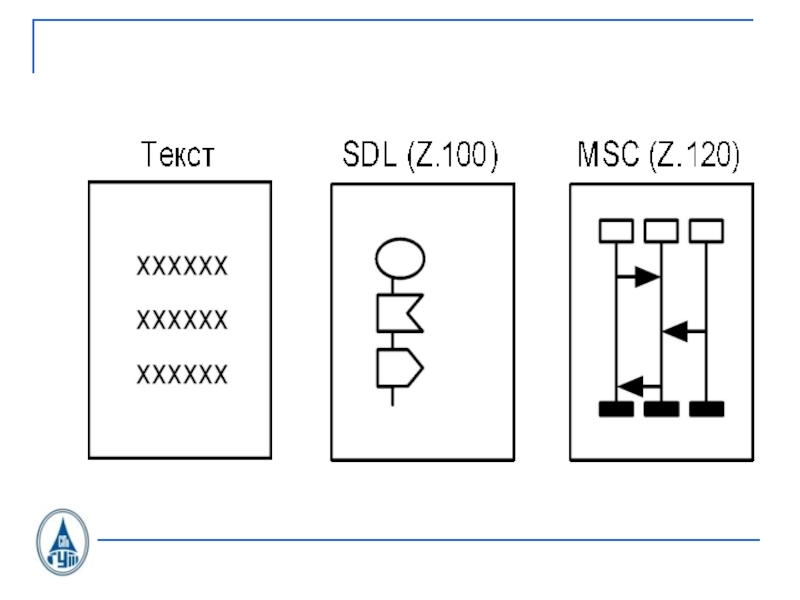
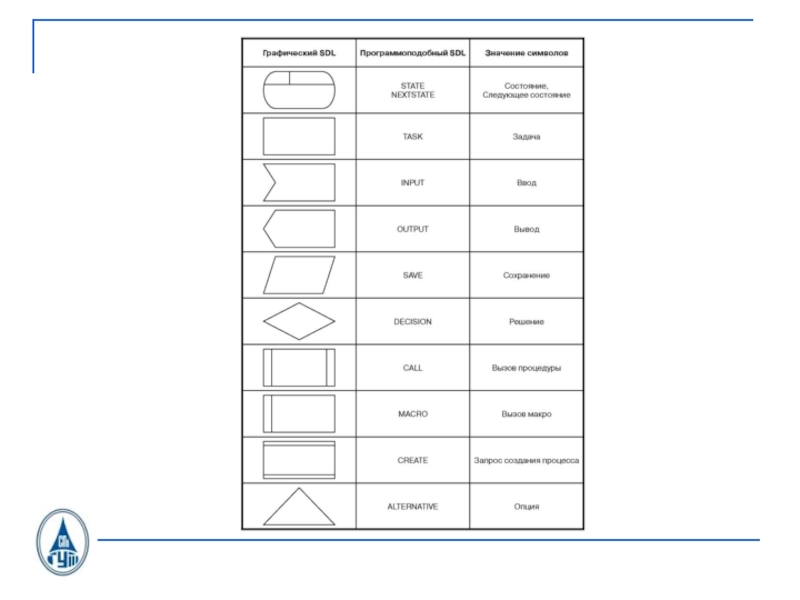
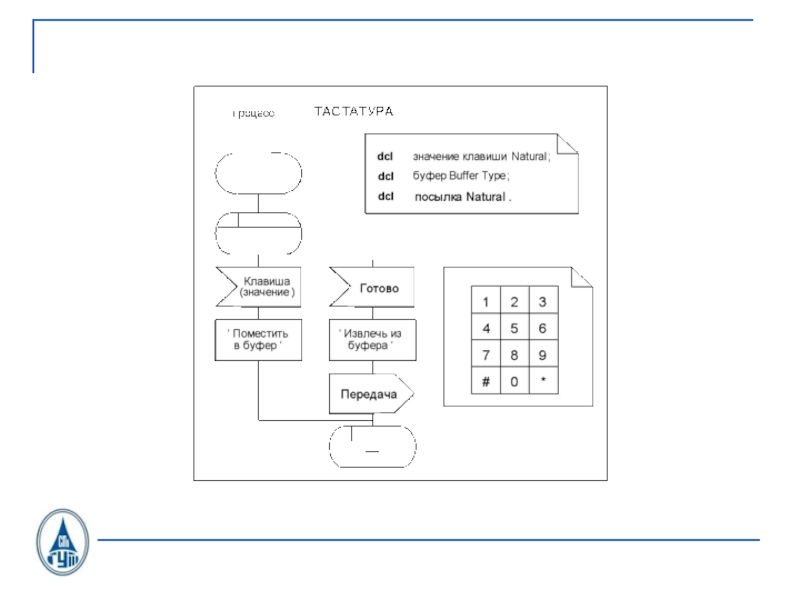
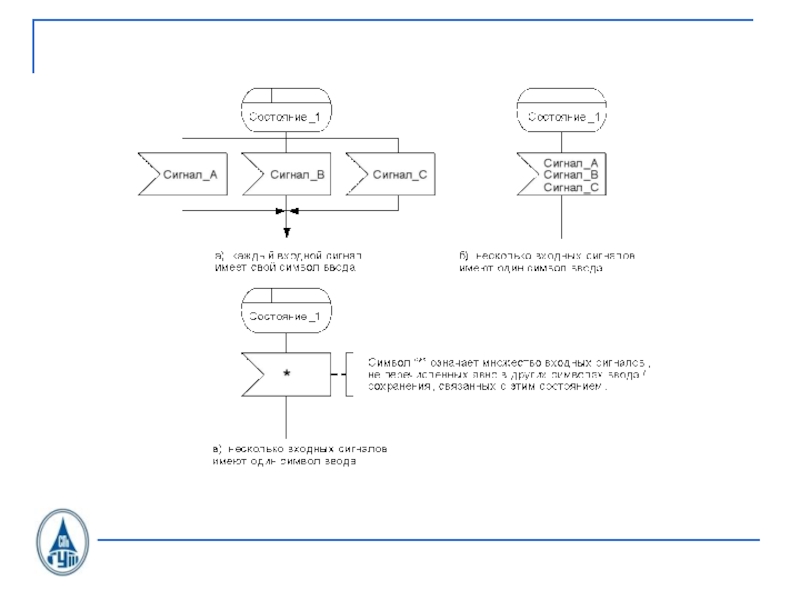
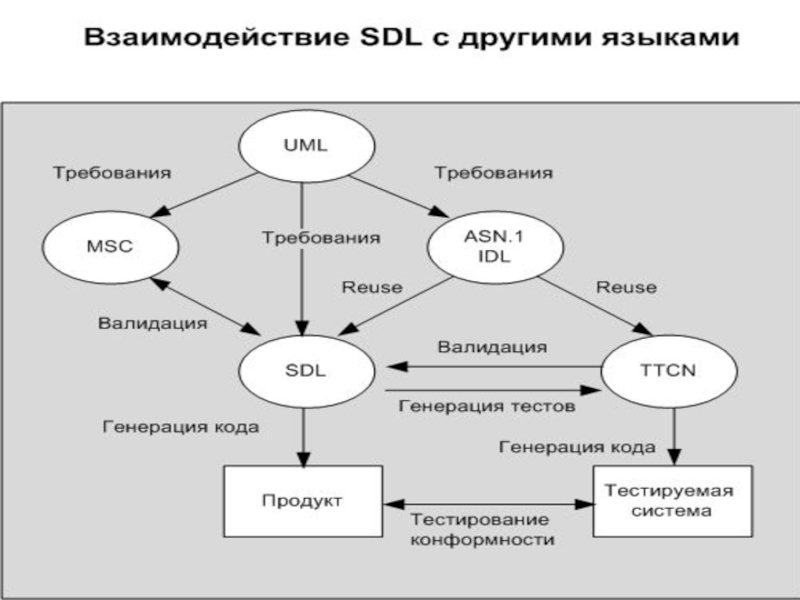
- 4. Язык описаний и спецификаций SDL. Язык
- 5. Слайд 5
- 6. Элементы теории спецификаций ПОРазличные способы задания языков
- 7. Конечные автоматыКонечный автомат – это пятеркаM =
- 8. Детерминированные конечные автоматыАвтомат называется детерминированным, если множество
- 9. Недетерминированные и конечные автоматыЛюбому недетерминированному автомату соответствует
- 10. Минимизация конечного автоматаКак найти автомат, эквивалентный данному,
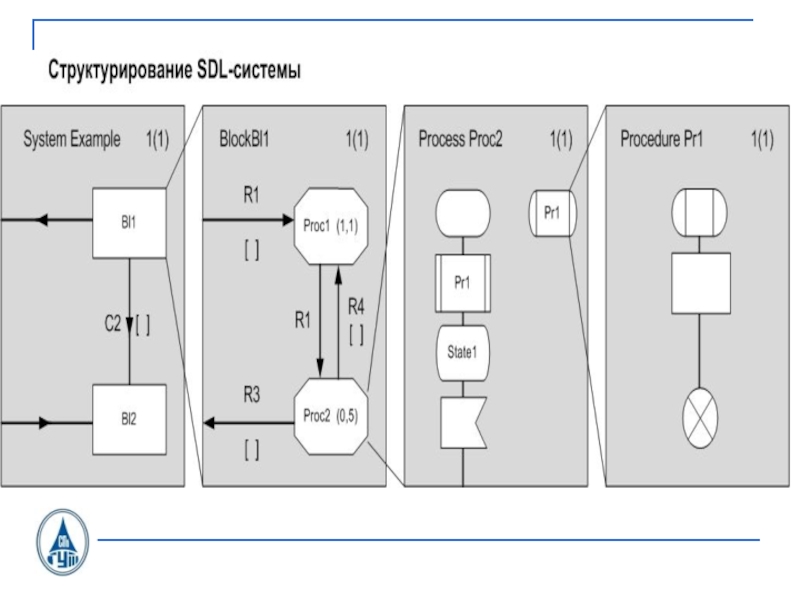
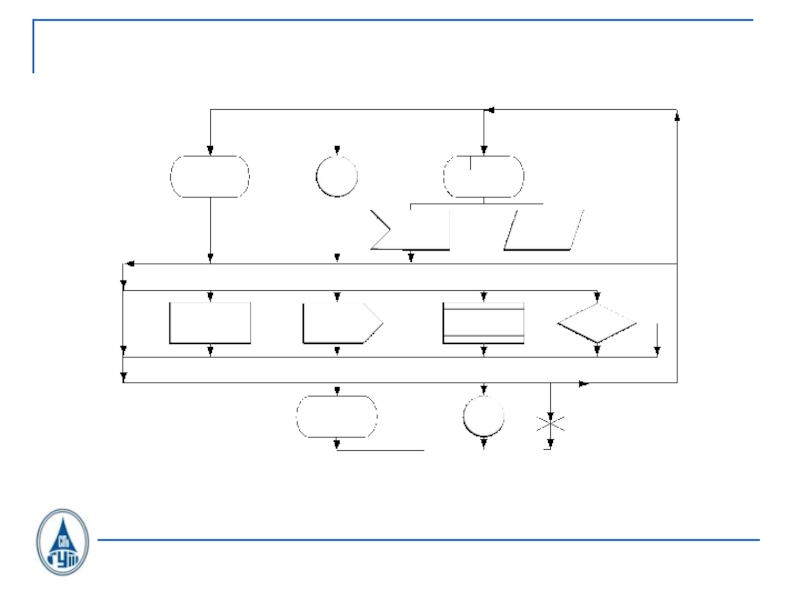
- 11. План:SDL-система SDL-блок SDL-процесс Синтаксис и семантика языка SDLПримеры
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
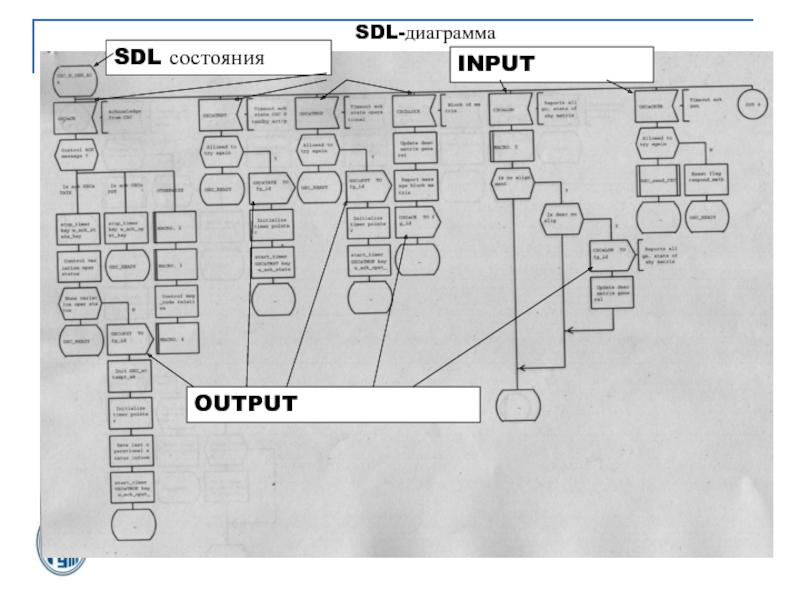
- 26. SDL состоянияINPUTOUTPUTSDL-диаграмма
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. Изложение этого материала в:[Л1]. Параграф 9.4.[Л2]. Параграф 2.1, 2.2 и 2.3
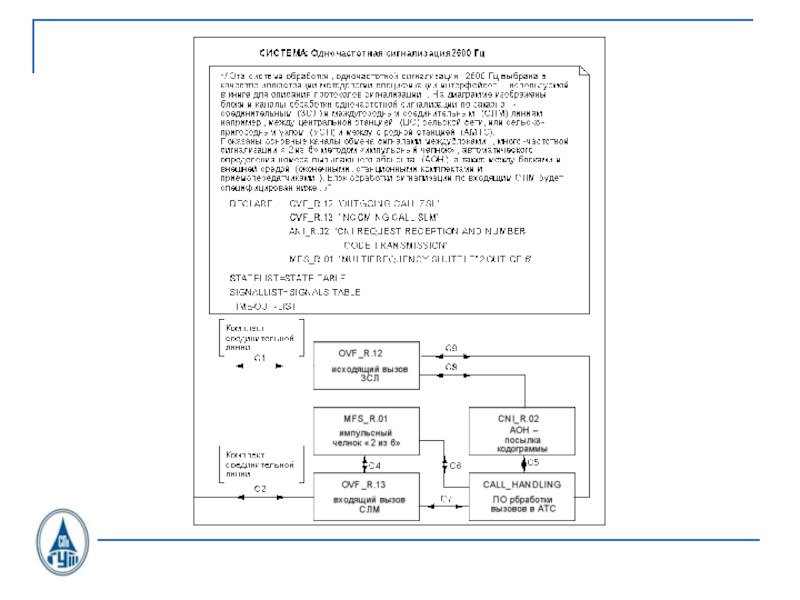
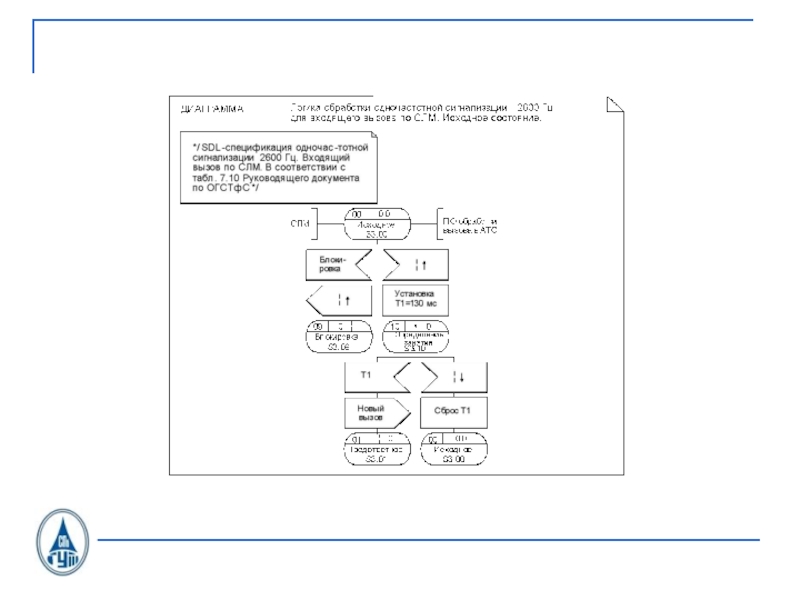
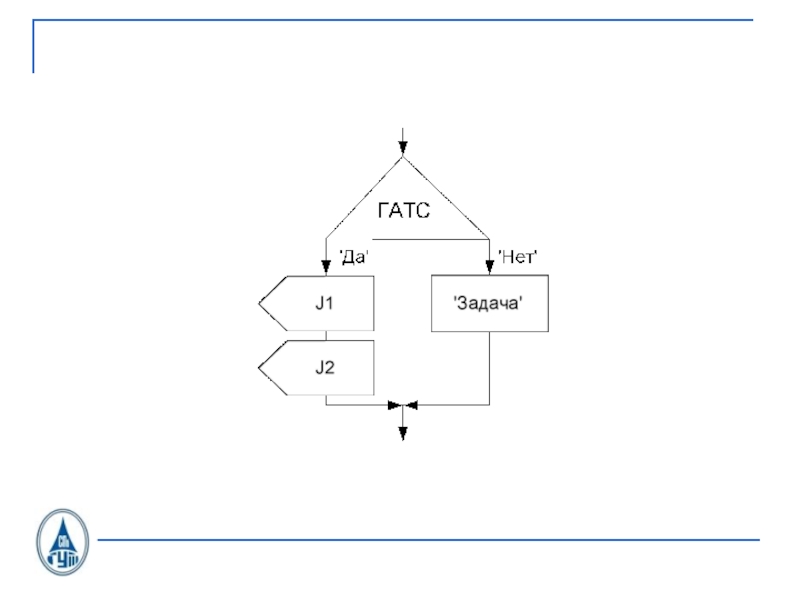
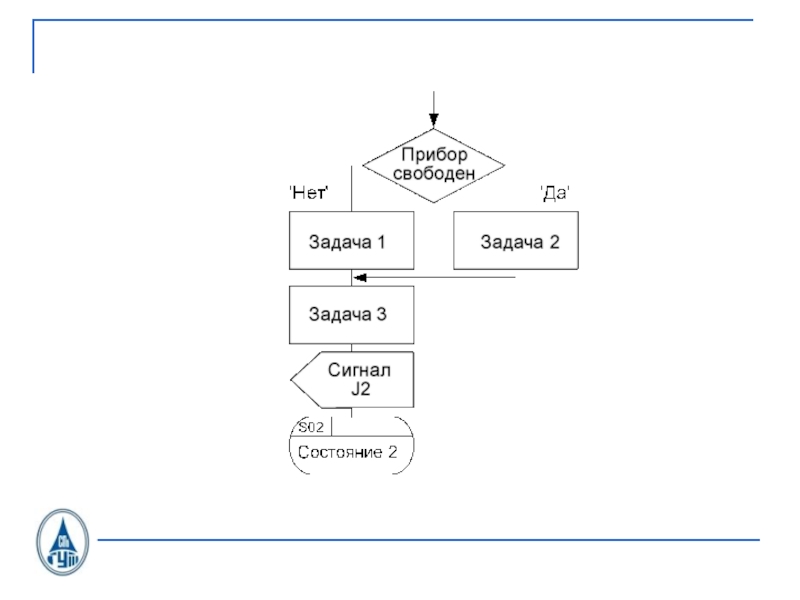
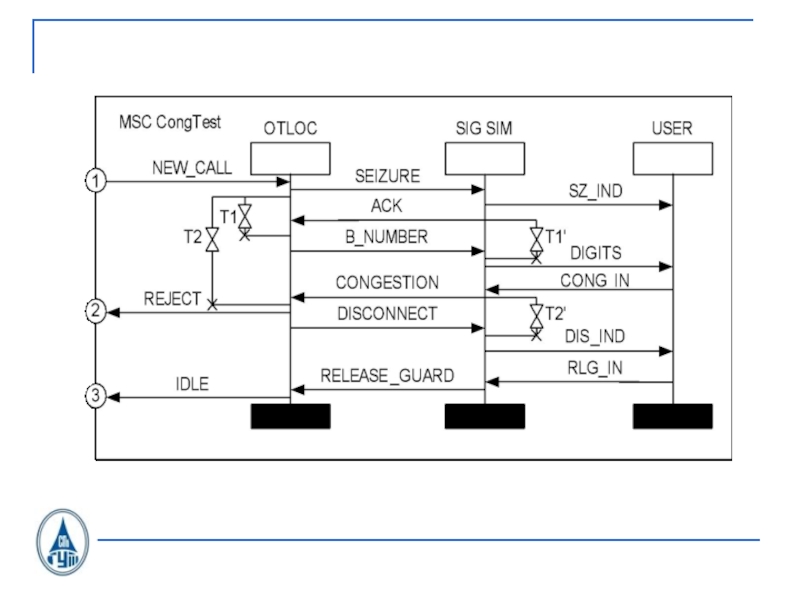
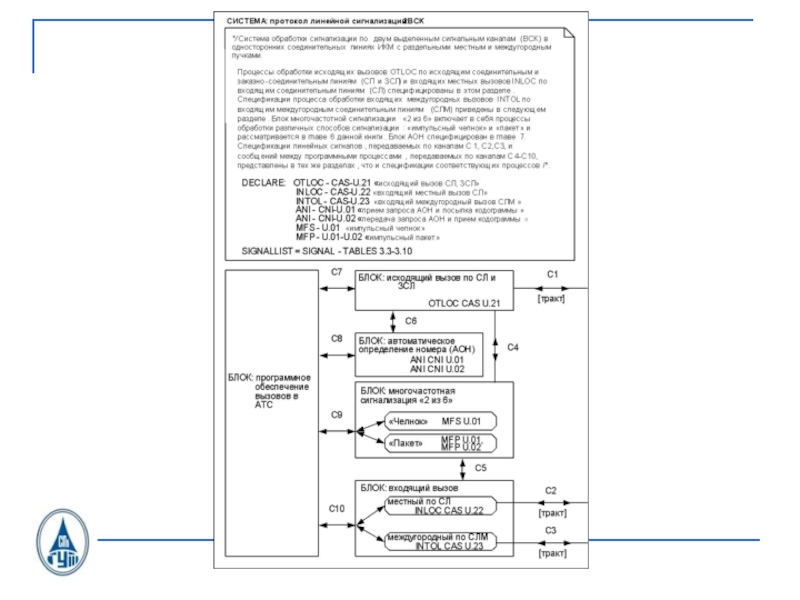
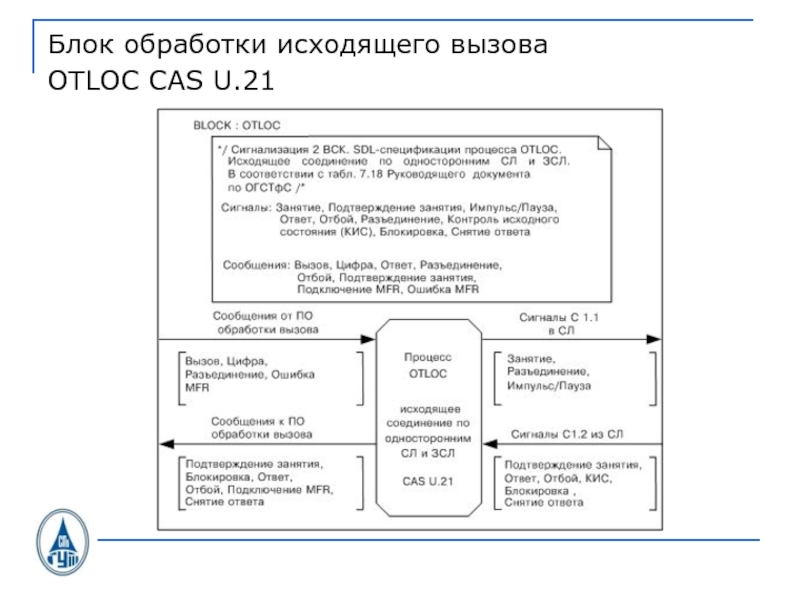
- 33. Блок обработки исходящего вызоваOTLOC CAS U.21
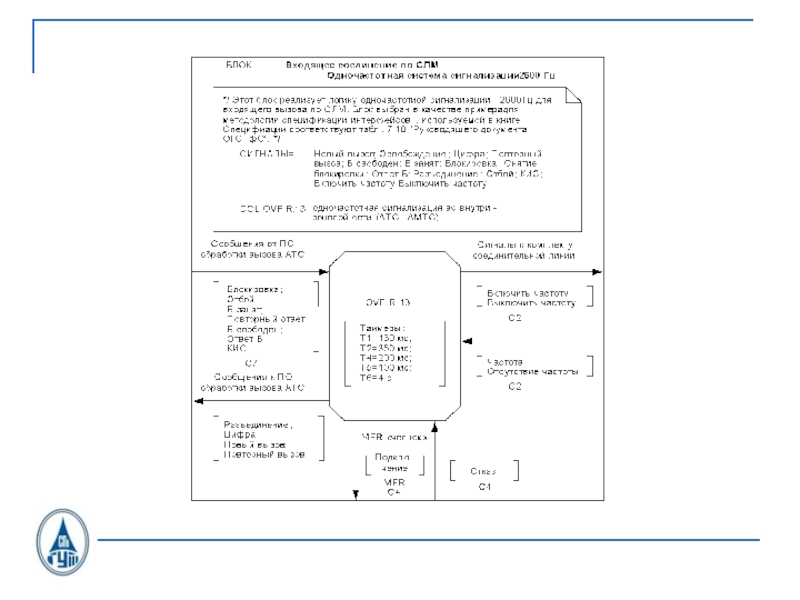
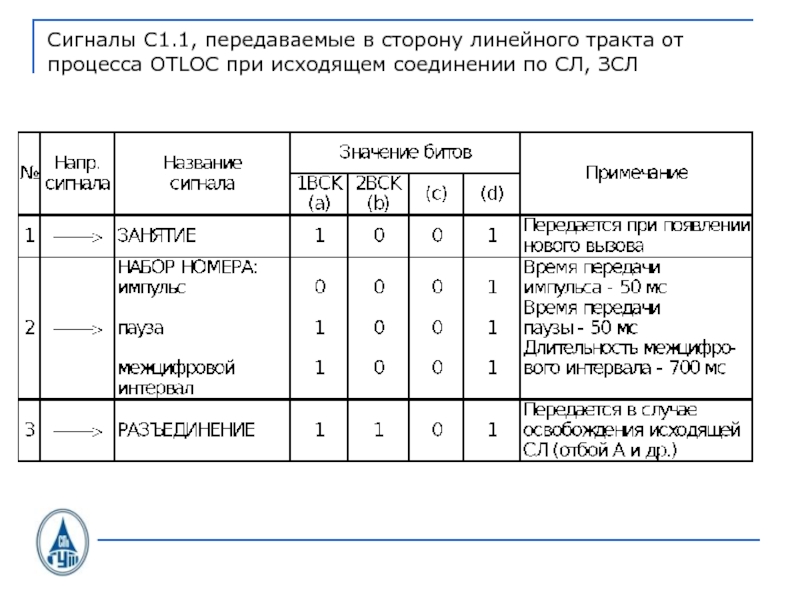
- 34. Сигналы С1.1, передаваемые в сторону линейного тракта от процесса OTLOC при исходящем соединении по СЛ, ЗСЛ
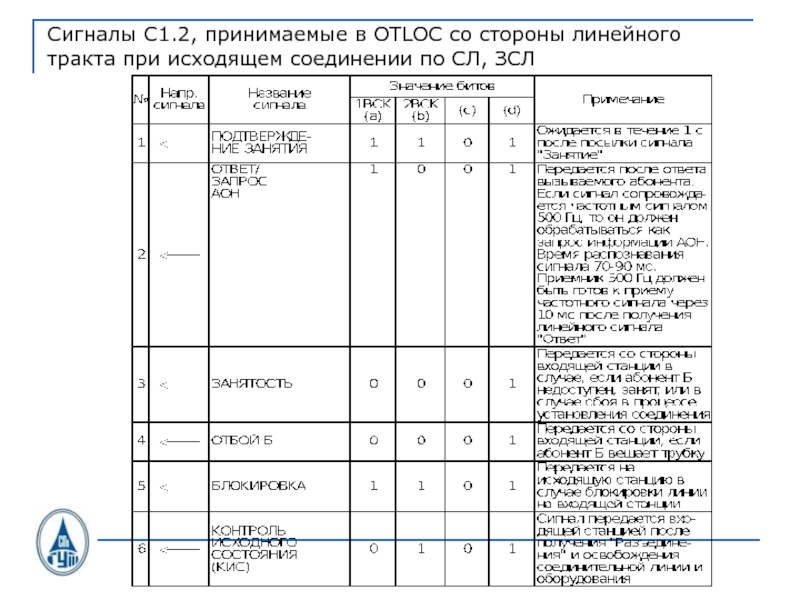
- 35. Сигналы С1.2, принимаемые в OTLOC со стороны линейного тракта при исходящем соединении по СЛ, ЗСЛ
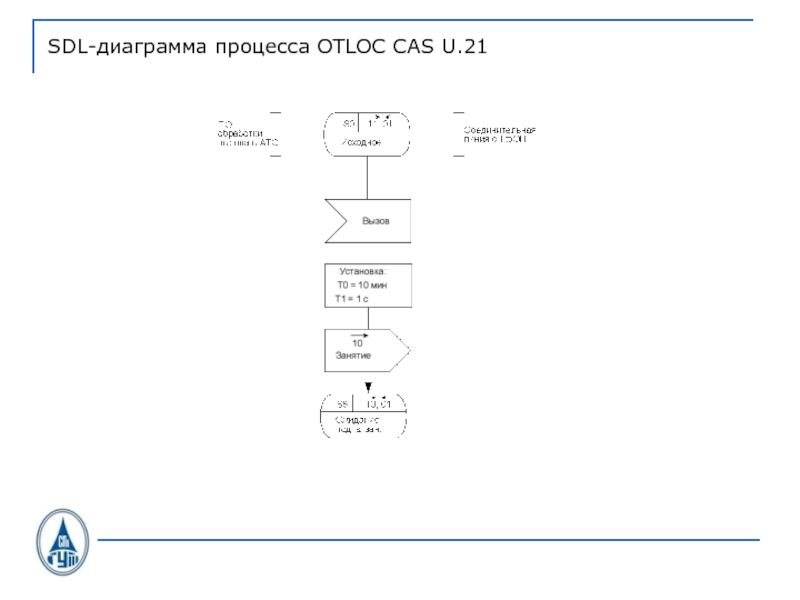
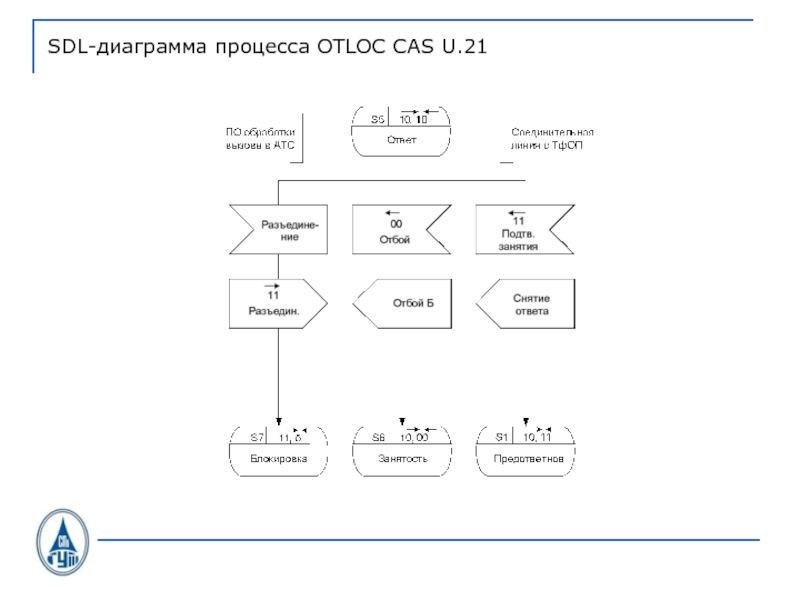
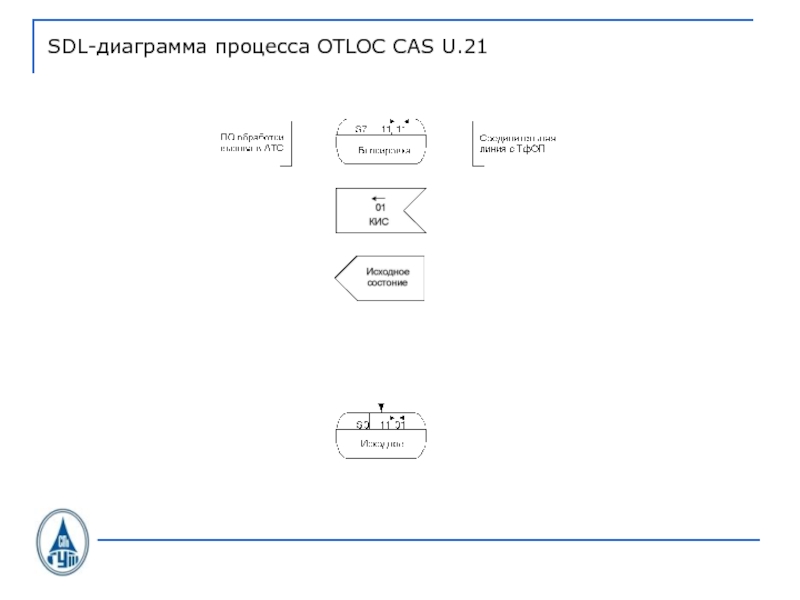
- 36. SDL-диаграмма процесса OTLOC CAS U.21
- 37. SDL-диаграмма процесса OTLOC CAS U.21
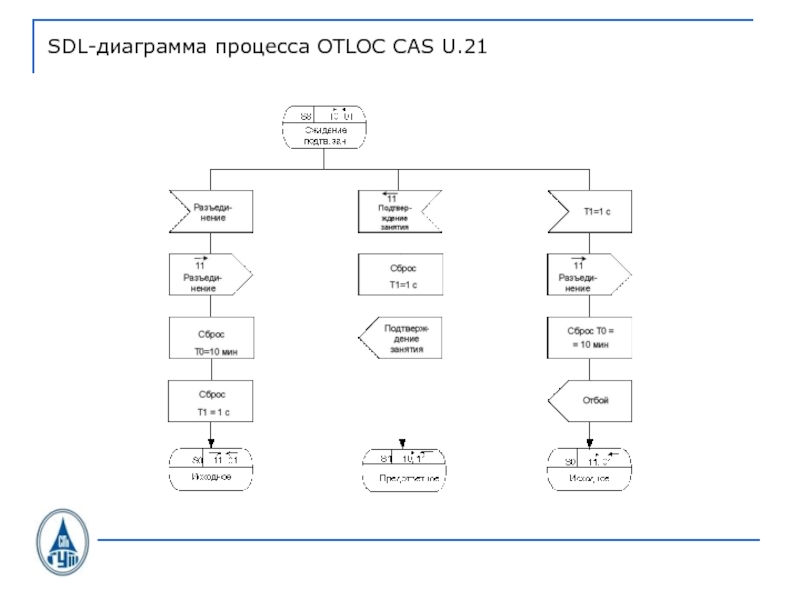
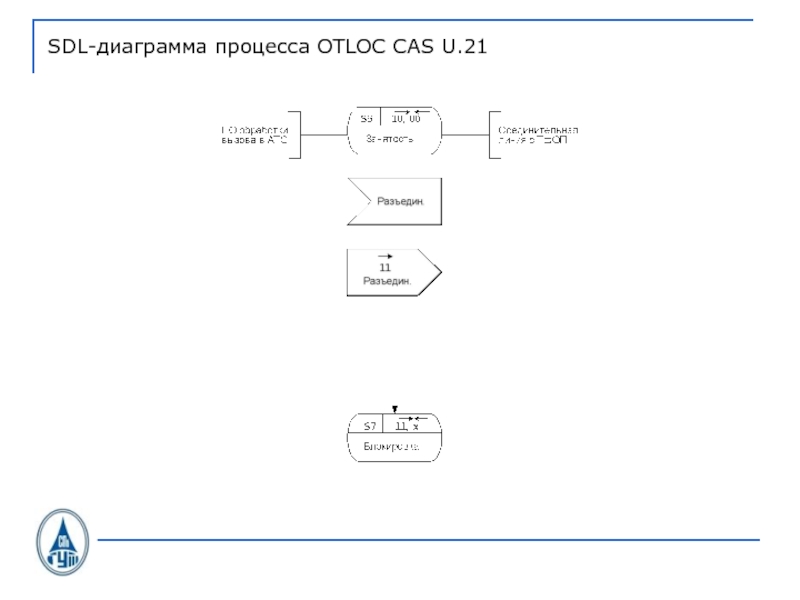
- 38. SDL-диаграмма процесса OTLOC CAS U.21
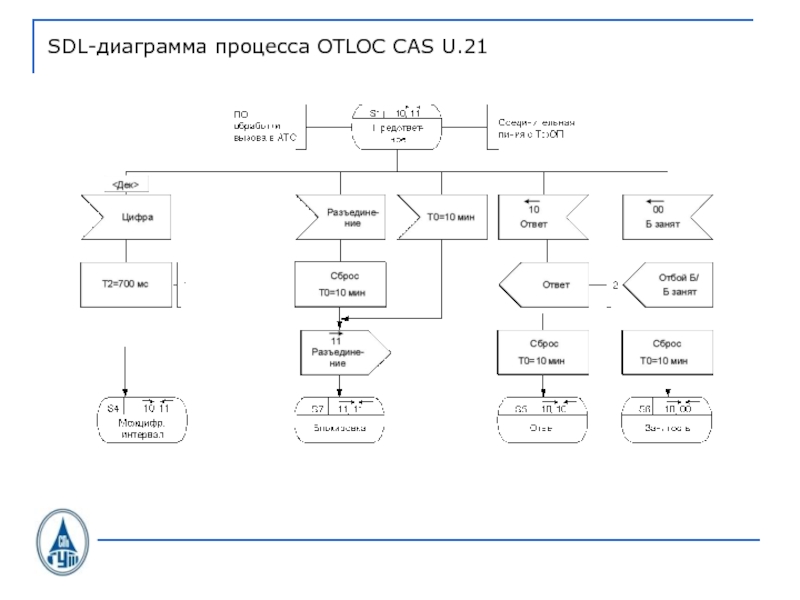
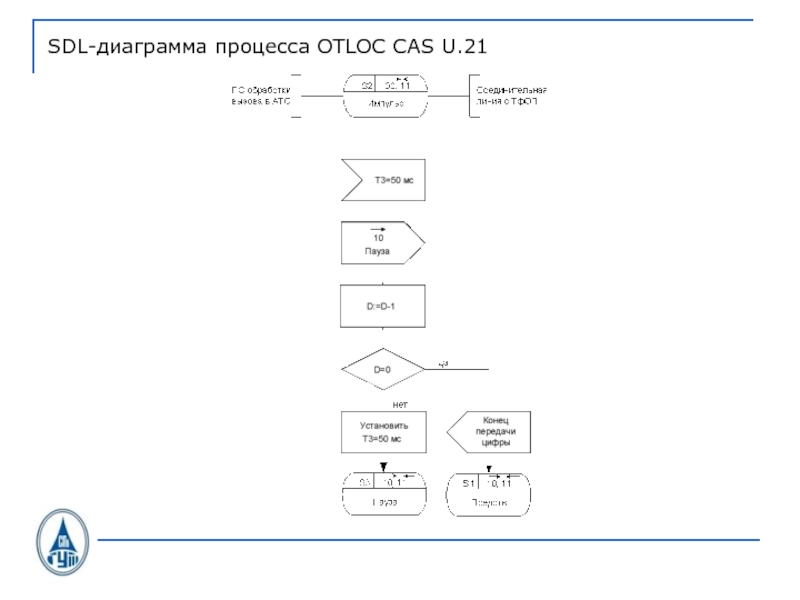
- 39. SDL-диаграмма процесса OTLOC CAS U.21
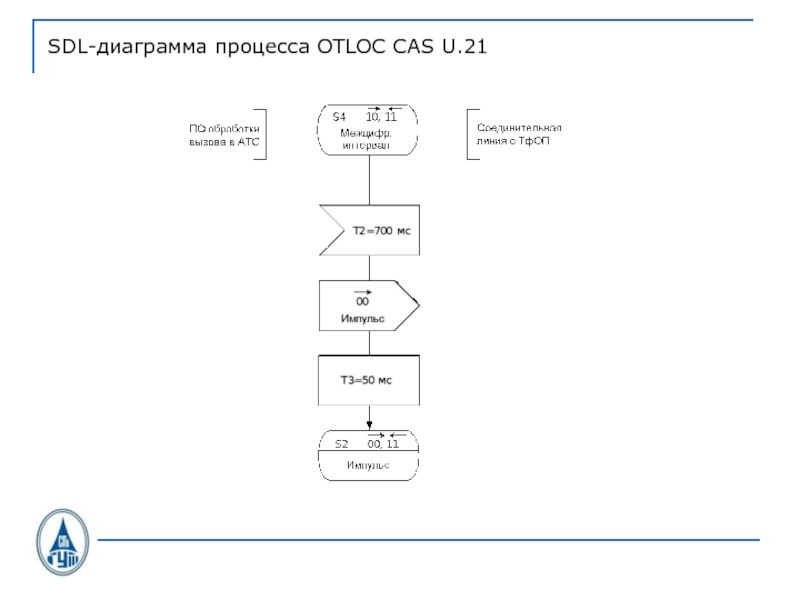
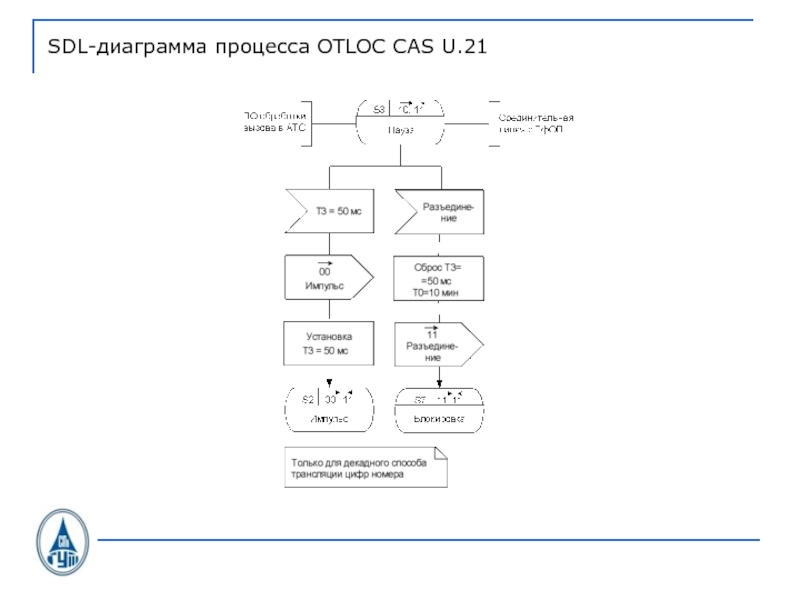
- 40. SDL-диаграмма процесса OTLOC CAS U.21
- 41. SDL-диаграмма процесса OTLOC CAS U.21
- 42. SDL-диаграмма процесса OTLOC CAS U.21
- 43. SDL-диаграмма процесса OTLOC CAS U.21
- 44. SDL-диаграмма процесса OTLOC CAS U.21
- 45. Изложение этого материала в:[Л1]. Параграф 8.2[Л2]. Параграф 3.2
- 46. Тема следующей лекции 4Входящий местный вызов.
- 47. Скачать презентанцию
Основная литератураЛ1. Гольдштейн Б.С. Системы коммутации. Учебник для ВУЗов. 2-е издание, доп. и испр.//СПб.: BHV-2004.Л2. Гольдштейн Б.С. Сигнализация в сетях связи. Том 1. 4-е издание. СПб.: BHV, 2005.
Слайды и текст этой презентации
Слайд 1
Учебный курс
Системы коммутации-1
Лекция 3
Международная стандартизация телекоммуникаций. Язык спецификаций и описаний
SDL. Язык MSC.
СС, СК и ВТ
Слайд 2Основная литература
Л1. Гольдштейн Б.С. Системы коммутации. Учебник для ВУЗов. 2-е
издание, доп. и испр.//СПб.: BHV-2004.
Л2. Гольдштейн Б.С. Сигнализация в сетях
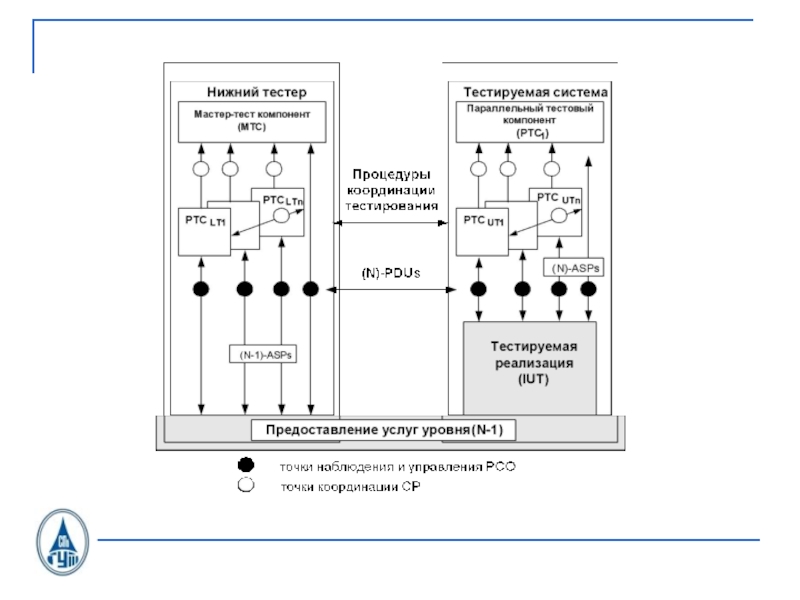
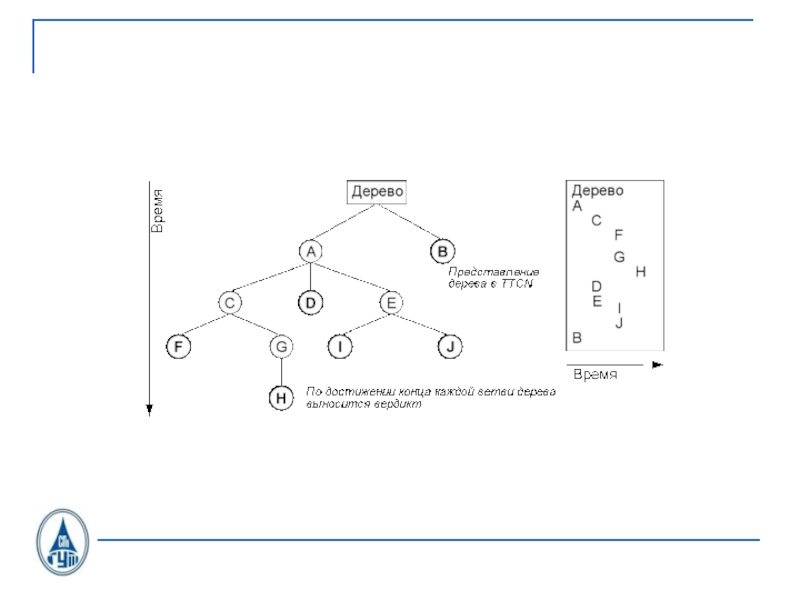
связи. Том 1. 4-е издание. СПб.: BHV, 2005.
![Изложение этого материала в:[Л1]. Параграф 1.7[Л2]. Параграф 2.3](/img/thumbs/b3c0ccf93522df89a3ab51726219e5c8-800x.jpg "Учебный курс Системы коммутации-1 Изложение этого материала в:[Л1]. Параграф 1.7[Л2]. Параграф 2.3")
Слайд 4 Язык описаний и спецификаций SDL. Язык MSC (Message Sequence Chart). Язык TTCN
(Tree and Tabular Combined Notation).
Язык ASN.1.
Слайд 6Элементы теории спецификаций ПО
Различные способы задания языков спецификаций:
Грамматики
Конечные автоматы
Спецификация должна
быть конечным
Должен существовать алгоритм, за конечное число шагов проверяющий принадлежность
некоторой входной спецификацииНаиболее распространенные формализмы для задания языков: грамматики, регулярные выражения, конечные и магазинные автоматы, машины Тьюринга
Слайд 7Конечные автоматы
Конечный автомат – это пятерка
M = (Q, Σ, δ,
q0, F), где
Q – конечное множество состояний
Σ – конечное множество
допустимых входных символовδ – функция перехода
q0 из Q – начальное состояние
F – множество заключительных состояний
Слайд 8Детерминированные конечные автоматы
Автомат называется детерминированным, если множество δ(q, a) содержит
не более одного состояния для любых q, a. Если δ(q,
a) всегда содержит ровно одно состояние, то автомат называется полностью определенным.Цепочка w допускается автоматом M, если существует последовательность шагов, приводящая нас по этой цепочке в заключительное состояние автомата
Язык распознается конечным автоматом, если им распознается каждое слово языка
Удобная форма записи конечных автоматов – диаграммы переходов
Слайд 9Недетерминированные и конечные автоматы
Любому недетерминированному автомату соответствует детерминированный автомат, определяющий
тот же самый язык, причем известен метод конструирования эквивалентного конечного
автоматаТаким образом, классы языков, задаваемых недетерминированными и детерминированными конечными автоматами, совпадают
Конечные автоматы – удобный формализм, так как их легко моделировать программно
Слайд 10Минимизация конечного автомата
Как найти автомат, эквивалентный данному, с минимальным числом
состояний?
Алгоритм минимизации конечного автомата выглядит так:
Вначале мы удаляем все
недостижимые состоянияЗатем разбиваем множество всех достижимых состояний на классы эквивалентности неразличимых состояний
Из каждого класса эквивалентности мы берем только по одному представителю
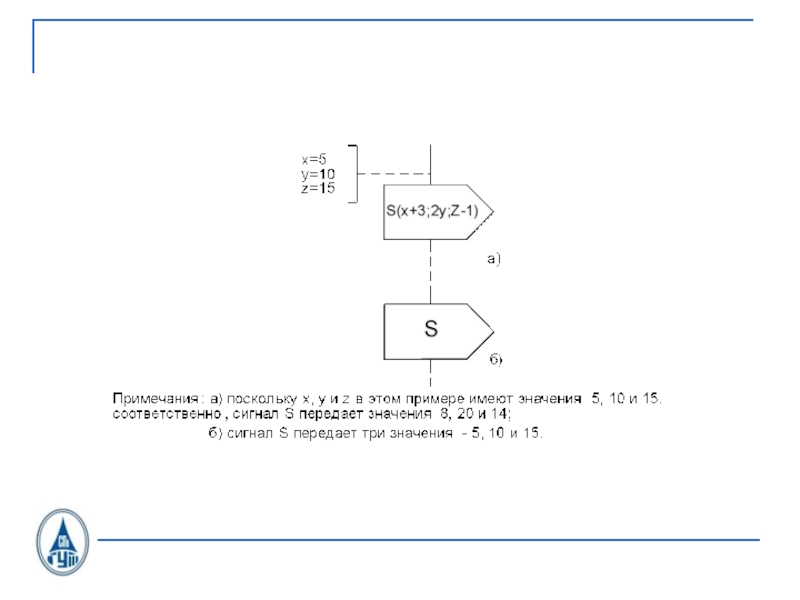
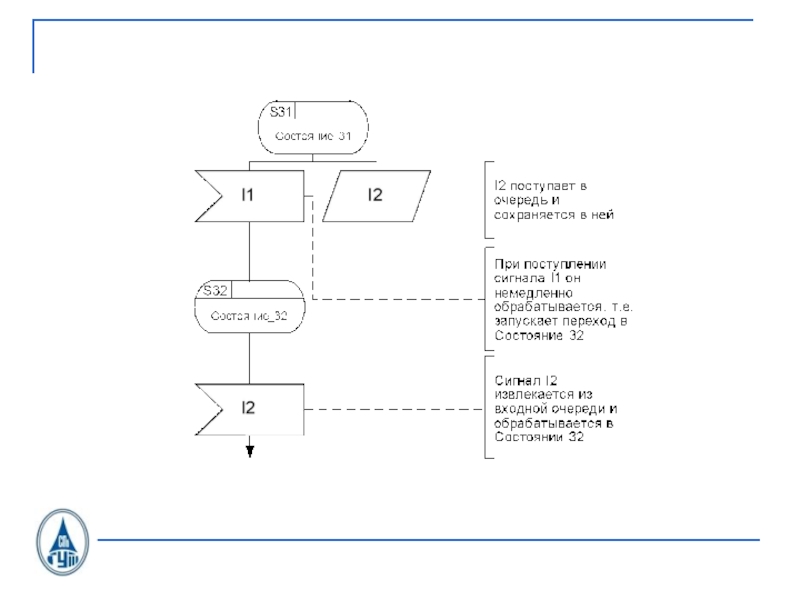
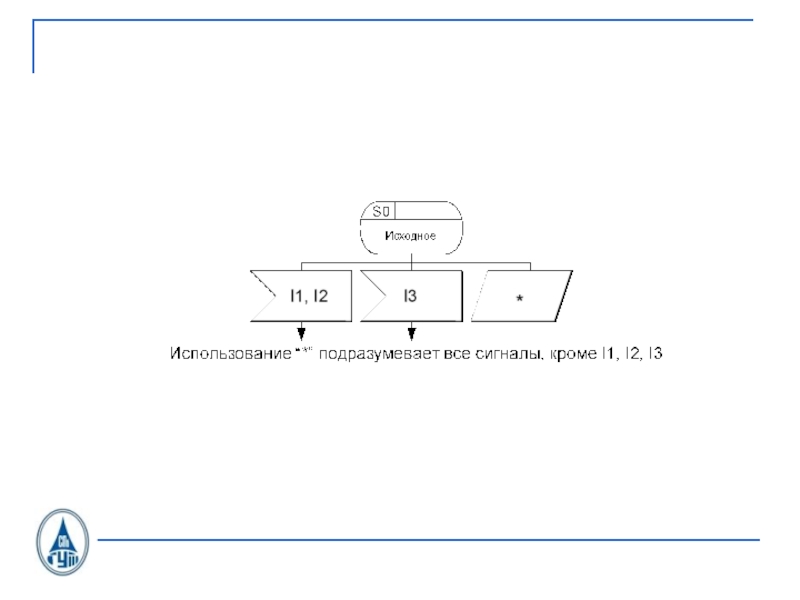
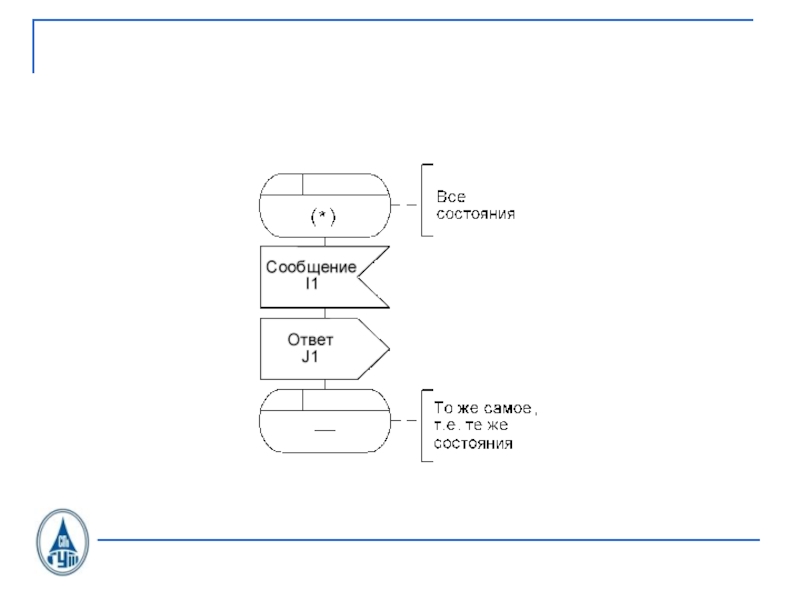
![Изложение этого материала в:[Л1]. Параграф 9.4.[Л2]. Параграф 2.1, 2.2 и 2.3](/img/thumbs/70da65eebd5ae83d42fe3baeb55fbdc1-800x.jpg "Учебный курс Системы коммутации-1 Изложение этого материала в:[Л1]. Параграф 9.4.[Л2]. Параграф 2.1, 2.2 и 2.3")
Слайд 34Сигналы С1.1, передаваемые в сторону линейного тракта от процесса OTLOC
при исходящем соединении по СЛ, ЗСЛ
Слайд 35Сигналы С1.2, принимаемые в OTLOC со стороны линейного тракта при
исходящем соединении по СЛ, ЗСЛ
![Изложение этого материала в:[Л1]. Параграф 8.2[Л2]. Параграф 3.2](/img/thumbs/4a50b1b6c5e55ae506809f13eb32d060-800x.jpg "Учебный курс Системы коммутации-1 Изложение этого материала в:[Л1]. Параграф 8.2[Л2]. Параграф 3.2")
