Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Улан-Удэ 2019 ЛОГИЧЕСКИЕ ОСНОВЫ КОМПЬЮТЕРА. ЭЛЕМЕНТЫ АЛГЕБРЫ
Содержание
- 1. Улан-Удэ 2019 ЛОГИЧЕСКИЕ ОСНОВЫ КОМПЬЮТЕРА. ЭЛЕМЕНТЫ АЛГЕБРЫ
- 2. Клод Шеннон (1916-2001). Его исследования позволили применить
- 3. Высказывание - это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.Высказывание
- 4. Высказывание или нет?
- 5. Алгебра логики определяет правила записи, вычисления значений,
- 6. Простые и сложные высказыванияВысказывания бывают простые и
- 7. Конъюнкция - логическая операция, ставящая в соответствие
- 8. Дизъюнкция - логическая операция, которая каждым двум
- 9. Инверсия - логическая операция, которая каждому высказыванию
- 10. Инверсия КонъюнкцияДизъюнкцияПриоритет выполнения логических операций: ¬, &, V.Основные логическиеоперации
- 11. Таблица истинности Решение логических выражений принято записывать в
- 12. Построение таблиц истинности для логических выраженийподсчитать n
- 13. А V A & Bn = 2,
- 14. Построим таблицу истинности для выражения: F = (A v B) & (¬ A v ¬ B)
- 15. Домашнее задание:выучить определения и построить таблицы истинности:
- 16. В естественном языке – «Если A, то
- 17. Логические операцииЛогическая эквивалентность (равнозначность) – это логическая
- 18. Логические задачи.Способы решения логических задач: средствами алгебры логики; табличный; с помощью рассуждений.
- 19. I. Решение логических задач средствами алгебры логики.Схема
- 20. Задача №1.Трое друзей, болельщиков автогонок "Формула-1", спорили
- 21. Слайд 21
- 22. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Улан-Удэ
2019
ЛОГИЧЕСКИЕ ОСНОВЫ КОМПЬЮТЕРА.
ЭЛЕМЕНТЫ АЛГЕБРЫ ЛОГИКИ.
Министерство образования и науки Республики Бурятия
Государственное
бюджетное профессиональное учреждение
Слайд 2Клод Шеннон (1916-2001). Его исследования позволили применить алгебру логики в
вычислительной технике
Логика
Аристотель (384-322 до н.э.). Основоположник формальной логики (понятие, суждение,
умозаключение). Джордж Буль (1815-1864). Создал новую область науки - Математическую логику (Булеву алгебру или Алгебру высказываний).
Слайд 3Высказывание - это предложение на любом языке, содержание которого можно
однозначно определить как истинное или ложное.
Высказывание
Слайд 5Алгебра логики определяет правила записи, вычисления значений, упрощения и преобразования
высказываний.
В алгебре логики высказывания обозначают буквами и называют логическими переменными.
Если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей (А = 1), а если ложно - нулём (В = 0).
0 и 1 называются логическими значениями.
Алгебра логики
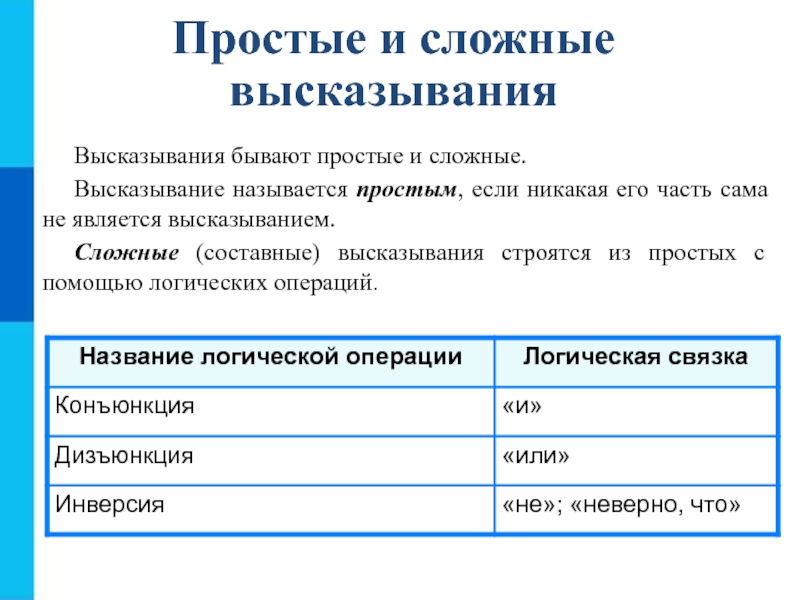
Слайд 6Простые и сложные высказывания
Высказывания бывают простые и сложные.
Высказывание называется простым,
если никакая его часть сама не является высказыванием.
Сложные (составные)
высказывания строятся из простых с помощью логических операций.Слайд 7Конъюнкция - логическая операция, ставящая в соответствие каждым двум высказываниям
новое высказывание, являющееся истинным тогда и только тогда, когда оба
исходных высказывания истинны.Другое название: логическое умножение.
Обозначения: , , &, И.
Логические операции
Таблица истинности:
Графическое представление
A
B
А&В
Слайд 8Дизъюнкция - логическая операция, которая каждым двум высказываниям ставит в
соответствие новое высказывание, являющееся ложным тогда и только тогда, когда
оба исходных высказывания ложны.Другое название: логическое сложение.
Обозначения: V, |, ИЛИ, +.
Логические операции
Таблица истинности:
Графическое представление
A
B
АVВ
Слайд 9Инверсия - логическая операция, которая каждому высказыванию ставит в соответствие
новое высказывание, значение которого противоположно исходному.
Другое название: логическое отрицание.
Обозначения: НЕ,
¬ , ¯ . Логические операции имеют следующий приоритет:
инверсия, конъюнкция, дизъюнкция.
Логические операции
Таблица истинности:
Графическое представление
A
Ā
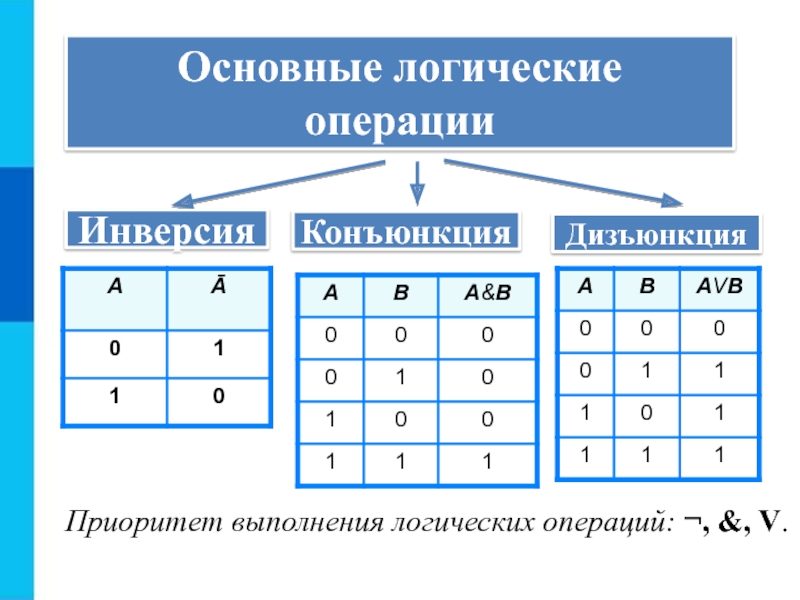
Слайд 10Инверсия
Конъюнкция
Дизъюнкция
Приоритет выполнения логических операций: ¬, &, V.
Основные логические
операции
Слайд 11Таблица истинности
Решение логических выражений принято записывать в виде таблиц истинности- таблиц,
в которых по действиям показано, какие значения принимает логическое выражение
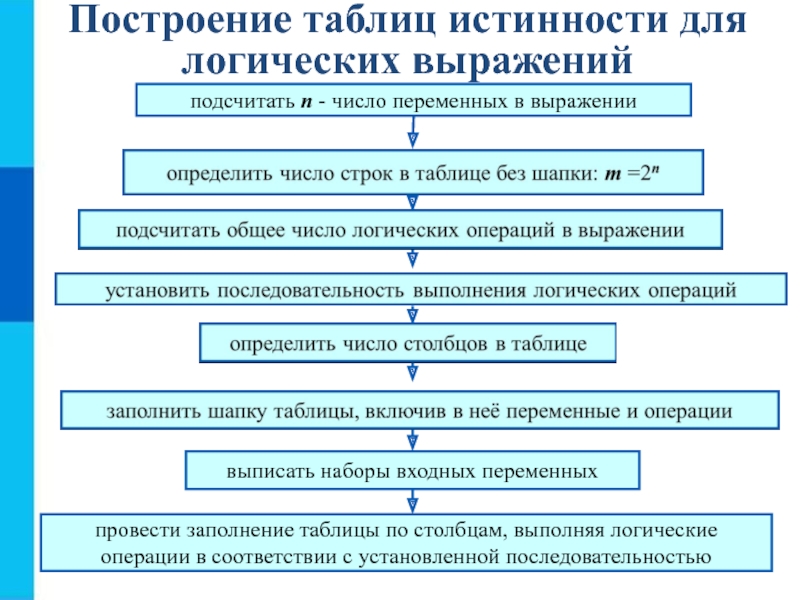
при всех возможных наборах его переменных.Слайд 12Построение таблиц истинности для логических выражений
подсчитать n - число переменных
в выражении
выписать наборы входных переменных
провести заполнение таблицы по столбцам, выполняя
логическиеоперации в соответствии с установленной последовательностью
Слайд 16В естественном языке – «Если A, то B»;
Обозначение – →
Логические
операции
Импликация – это логическая операция, ставящая в соответствие каждым двум
простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.Таблица истинности:
Слайд 17Логические операции
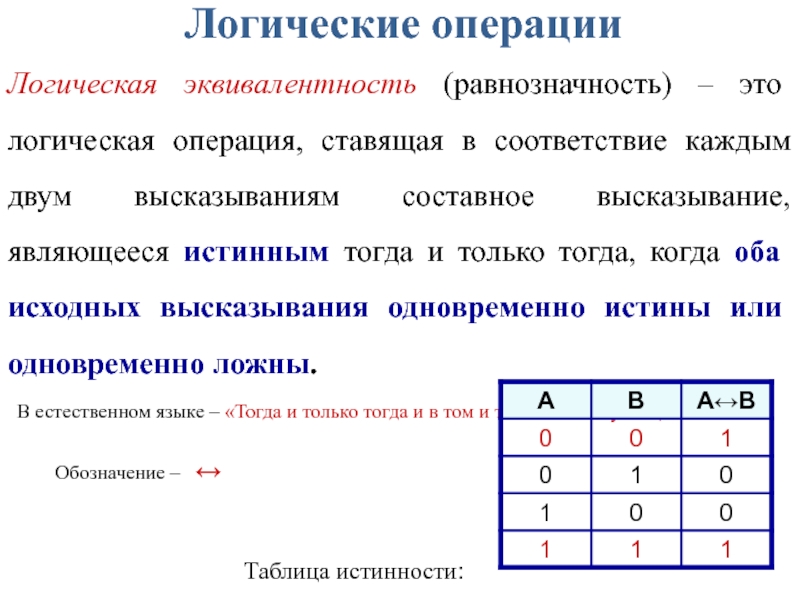
Логическая эквивалентность (равнозначность) – это логическая операция, ставящая в
соответствие каждым двум высказываниям составное высказывание, являющееся истинным тогда и
только тогда, когда оба исходных высказывания одновременно истины или одновременно ложны.В естественном языке – «Тогда и только тогда и в том и только том случае»;
Обозначение – ↔
Таблица истинности:
Слайд 18Логические задачи.
Способы решения логических задач:
средствами алгебры логики;
табличный;
с помощью рассуждений.
Слайд 19I. Решение логических задач средствами алгебры логики.
Схема решения:
Изучается условие
задачи;
Вводится система обозначений для логических высказываний;
Конструируется логическая формула,
описывающая логические связи между всеми высказываниями условия задачи;Определяются значения истинности этой логической формулы;
Из полученных значений истинности формулы определяются значения истинности введённых логических высказываний, на основании которых делается заключение о решении.
Слайд 20Задача №1.
Трое друзей, болельщиков автогонок "Формула-1", спорили о результатах предстоящего
этапа гонок.
— Вот увидишь, Шумахер не придет первым, — сказал
Джон. Первым будет Хилл.— Да нет же, победителем будет, как всегда, Шумахер, — воскликнул Ник. — А об Алези и говорить нечего, ему не быть первым.
Питер, к которому обратился Ник, возмутился:
— Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину.
По завершении этапа гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл этап гонки?