TheSlide.ru

Уравнение касательной к графику функции

Содержание

1. Уравнение касательной к графику функции
2. Верно ли определение?Касательная – это прямая, имеющая с данной кривой одну общую точку.
3. Пусть дана и две
4. На данном уроке: Познакомимся с
5. Правила дифференцированияПроизводная суммы равна сумме производных.Постоянный множитель
6. Основные формулы дифференцирования
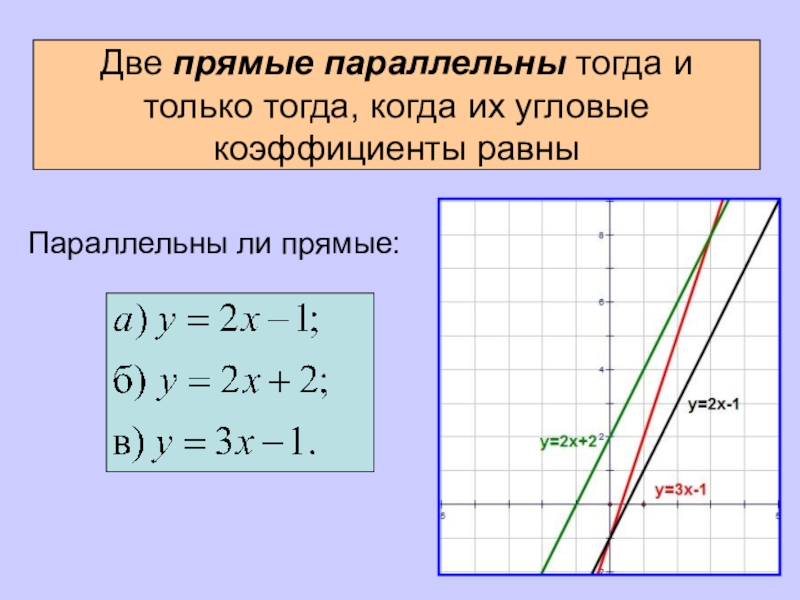
7. Две прямые параллельны тогда и только тогда, когда их угловые коэффициенты равныПараллельны ли прямые:
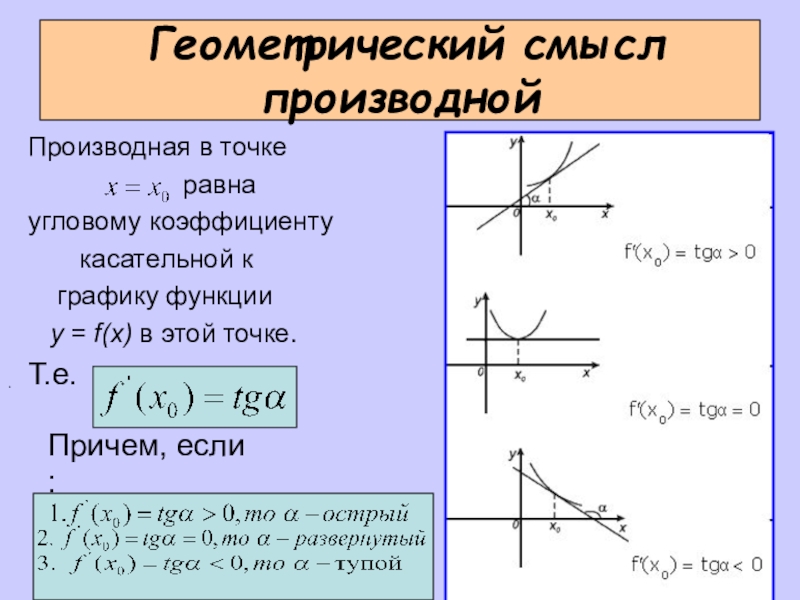
8. Геометрический смысл производнойПроизводная в точке
9. Уравнение касательнойДана функция уравнение касательной к графику функции
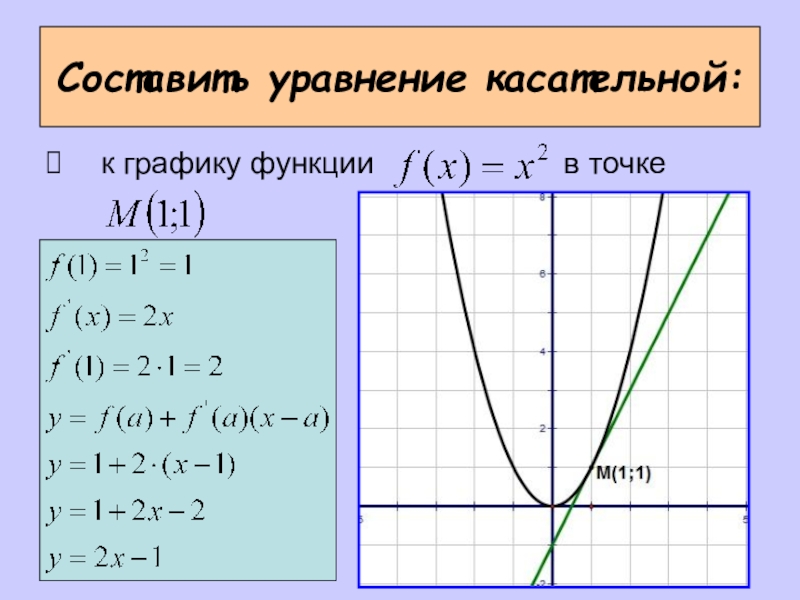
10. Составить уравнение касательной:к графику функции
11. Алгоритм нахождения уравнения касательной к графику функции
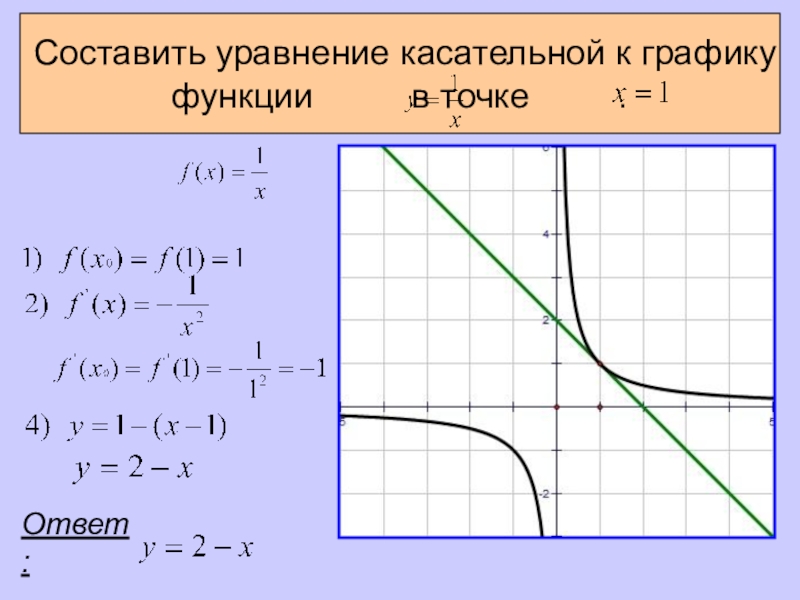
12. Составить уравнение касательной к графику функции
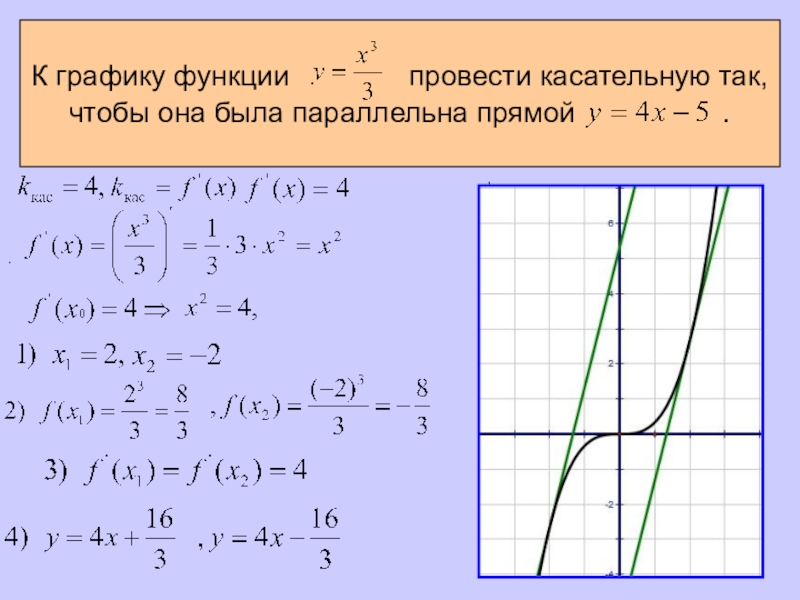
13. К графику функции
14. Ответьте на вопросы:В чем заключается геометрический смысл производной?Сформулируйте алгоритм нахождения уравнения касательной?
15. Скачать презентанцию

Верно ли определение?Касательная – это прямая, имеющая с данной кривой одну общую точку.

Главная
Разное
Уравнение касательной к графику функции

Слайды и текст этой презентации

Слайд 1Уравнение касательной к графику функции

Уравнение касательной к графику функции

Слайд 2Верно ли определение?

Касательная – это прямая, имеющая с данной кривой

одну общую точку.

Верно ли определение?Касательная – это прямая, имеющая с данной кривой одну общую точку.

Слайд 3Пусть дана и две прямые

и , имеющая

с данной параболой одну общую точку М (1;1).

Пусть дана и две прямые и

Слайд 4На данном уроке:
Познакомимся с уравнением касательной .

Научимся составлять уравнение касательной.
Для этого:
вспомним общий вид уравнения прямой
условия параллельности

прямых
правила дифференцирования
Формулы дифференцирования

На данном уроке: Познакомимся с уравнением касательной . Научимся составлять уравнение касательной.Для этого:вспомним общий вид

Слайд 5Правила дифференцирования
Производная суммы равна сумме производных.

Постоянный множитель можно вынести за

знак производной.

Производная произведения двух функций равна сумме двух слагаемых; первое

слагаемое есть произведение производной первой функции на вторую функцию, а второе слагаемое есть произведение первой функции на производную второй функции.

Производная частного

Правила дифференцированияПроизводная суммы равна сумме производных.Постоянный множитель можно вынести за знак производной.Производная произведения двух функций равна сумме

Слайд 6Основные формулы дифференцирования

Основные формулы дифференцирования

Слайд 7Две прямые параллельны тогда и только тогда, когда их угловые

коэффициенты равны
Параллельны ли прямые:

Две прямые параллельны тогда и только тогда, когда их угловые коэффициенты равныПараллельны ли прямые:

Слайд 8 Геометрический смысл производной
Производная в точке

равна
угловому коэффициенту

касательной к
графику функции
y = f(x) в этой точке.
Т.е.

Причем, если :

.

Геометрический смысл производнойПроизводная в точке равна

Слайд 9Уравнение касательной
Дана функция
уравнение касательной к
графику функции

Уравнение касательнойДана функция уравнение касательной к графику функции

Слайд 10Составить уравнение касательной:
к графику функции

в точке

Составить уравнение касательной:к графику функции в точке

Слайд 11Алгоритм нахождения уравнения касательной к графику функции y=f(x).
Вычислим

.
Найдем

Вычислим
Подставим найденные числа a , в формулу

Алгоритм нахождения уравнения касательной к графику функции y=f(x).Вычислим .Найдем

Слайд 12Составить уравнение касательной к графику функции

в точке .
Ответ:

Составить уравнение касательной к графику функции в точке .Ответ:

Слайд 13К графику функции

провести касательную так, чтобы она была параллельна прямой

.

.

,

,

,

,

.

К графику функции провести касательную так, чтобы она была параллельна

Слайд 14Ответьте на вопросы:

В чем заключается геометрический смысл производной?
Сформулируйте алгоритм нахождения

уравнения касательной?

Ответьте на вопросы:В чем заключается геометрический смысл производной?Сформулируйте алгоритм нахождения уравнения касательной?

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей