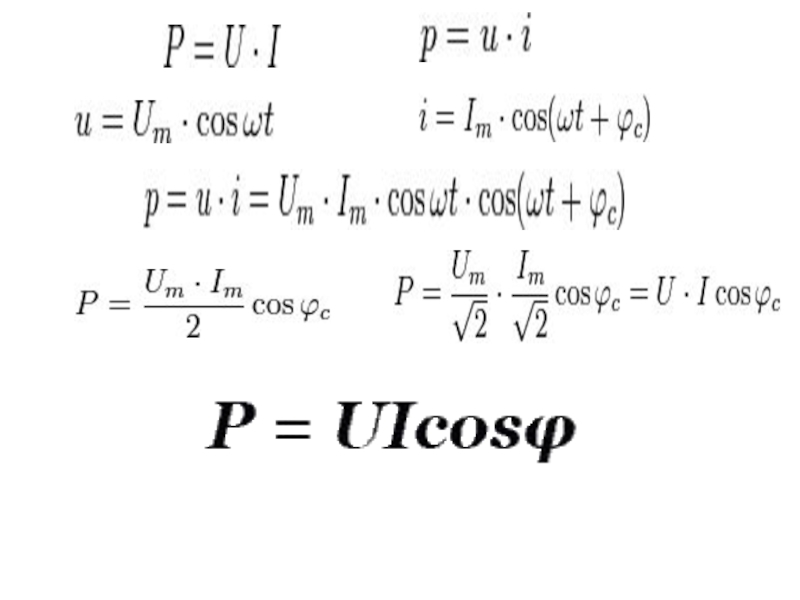Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
I.2. Электрические цепи переменного тока
Содержание
- 1. I.2. Электрические цепи переменного тока
- 2. КартофелечисткаПротирочная машинаЭлектромясорубкаТестомесильная машинаХлеборезка
- 3. Электрический ток величина и направление которого меняются
- 4. Основано на явлении ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ. Токопроводящую рамку
- 5. Слайд 5
- 6. Согласно ЗАКОНУ ФАРАДЕЯ для электромагнитной индукции, при
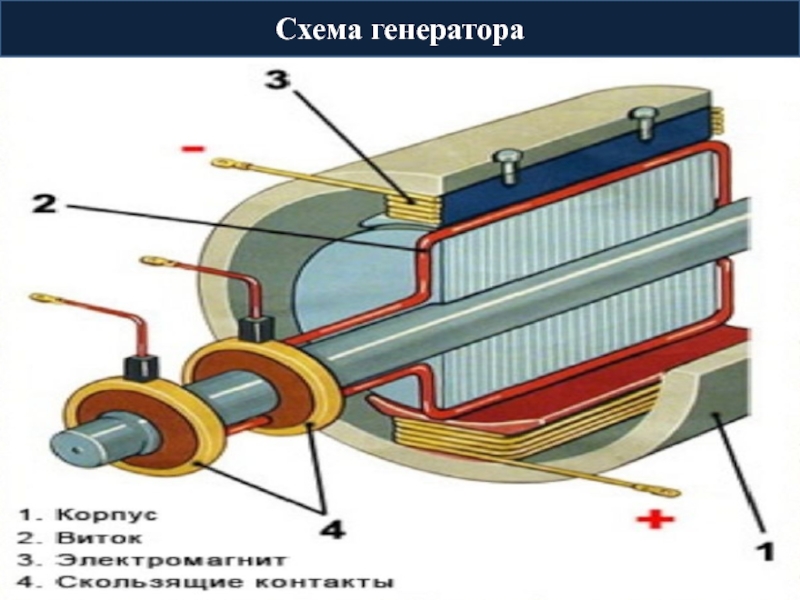
- 7. Схема генератора
- 8. ИТАК! ПЕРЕМЕННЫЙ ТОК – это электрический ток, который
- 9. Фаза колебаний силы тока может не совпадать
- 10. 1.3. Действующие значения напряжения и силы тока
- 11. Когда говорят, что напряжение в городской электрической
- 12. Переменный ток представляет собой вынужденные электромагнитные колебания,
- 13. Для учета процессов преобразования электромагнитной энергии в
- 14. Слайд 14
- 15. ЕМКОСТЬ И ИНДУКТИВНОСТЬ являются реактивными приемниками энергии или реактивными элементами.
- 16. 2.1. Активные элементыИДЕАЛИЗИРОВАННЫМ ИСТОЧНИКОМ ТОКА называют элемент
- 17. 2.1.2. Источник напряжения (ЭДС) ИДЕАЛИЗИРОВАННЫМ ИСТОЧНИКОМ НАПРЯЖЕНИЯ
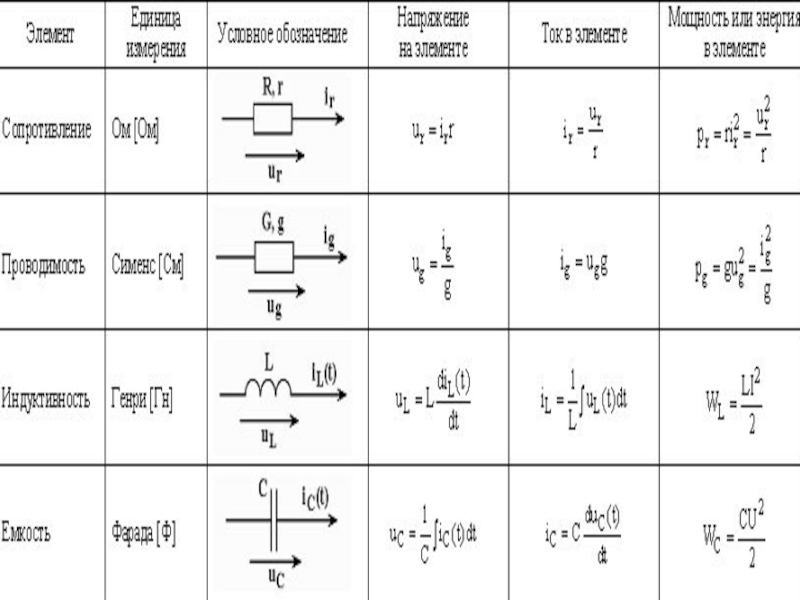
- 18. 2.2.1. Сопротивление Отношение, определяющее сопротивление: ur =
- 19. 2.2.2. Проводимость ПРОВОДИМОСТЬЮ называется величина, обратная сопротивлению: G = 1/R. Единица измерения – СИМЕНС (См).
- 20. 2.2.3. Емкость Отношение, определяющее емкость: Величина С
- 21. Величина заряда на конденсаторе определяется по формуле:
- 22. 2.2.4. Индуктивность Отношение, определяющее индуктивность: Величина L
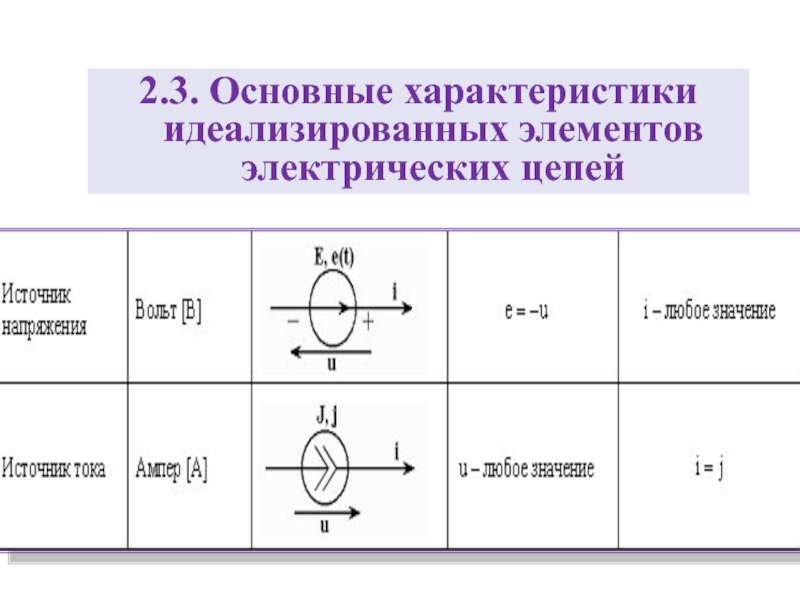
- 23. 2.3. Основные характеристики идеализированных элементов электрических цепей
- 24. Слайд 24
- 25. Основные характеристики идеализированных элементов электрических цепей
- 26. 1) Заданное сопротивление обычно обеспечивают включением специального
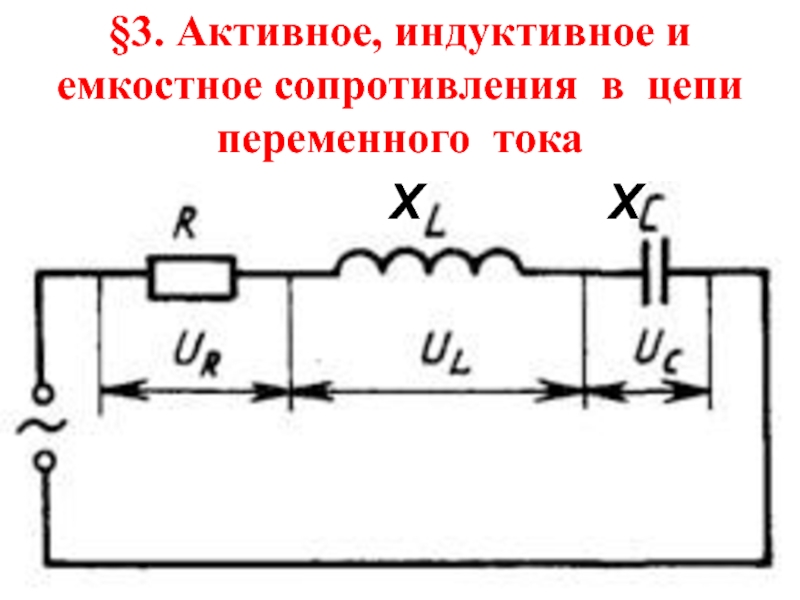
- 27. §3. Активное, индуктивное и емкостное сопротивления в цепи переменного токаХХ
- 28. Конденсатор в цепи постоянного тока (ток
- 29. В цепях переменного тока различают три вида
- 30. В цепи течет ток заряда или разряда
- 31. Электрические устройства, преобразующие электрическую энергию во внутреннюю,
- 32. При небольших значениях частоты переменного тока активное
- 33. 2.2. Векторная диаграмма при наличии в
- 34. 2.3. Конденсатор в цепи переменного токаПусть на
- 35. ОТСЮДАСледовательно, колебания напряжения на обкладках конденсатора в
- 36. Колебания силы тока на конденсаторе опережают
- 37. Отношение амплитуды колебаний напряжения на конденсаторе к
- 38. Векторная диаграмма при наличии в цепи переменного тока только емкостного сопротивления
- 39. 2.4. Индуктивность в цепи переменного тока Индуктивность
- 40. ТОГДА:Таким образом, колебания напряжения на индуктивности ОПЕРЕЖАЮТ
- 41. векторная диаграммаЕсли индуктивность измеряется в Генри, а
- 42. Колебания силы тока на катушке
- 43. ВЕКТОРНАЯ ДИАГРАММА при наличии в цепи переменного
- 44. 2.5. Закон Ома для переменного тока Электрическая
- 45. С учетом сдвига фаз между UR,UC и
- 46. Таким образом, полное напряжение между концами цепи
- 47. Амплитуду полного напряжения можно найти как модуль
- 48. Вектор U0 образует с осью токов угол
- 49. При наличии в цепи переменного тока
- 50. §4. Синусоидальные функции в комплексной форме Комплексное
- 51. КОМПЛЕКСНОЕ ЧИСЛО м. б. представлено в виде
- 52. 3.1. Пример
- 53. Действующие значения напряжения и силы
- 54. Слайд 54
- 55. 1.Если в цепи переменного тока только
- 56. МОЩНОСТЬ в цепи переменного тока определяется теми
- 57. явление в электрической цепи, содержащей индуктивные и
- 58. Цепи, в которых используется эффект резонанса, называются
- 59. где - ХАРАКТЕРИСТИЧЕСКОЕ СОПРОТИВЛЕНИЕ контура 6.1.
- 60. Отношение величины электромагнитной энергии, запасенной на реактивных
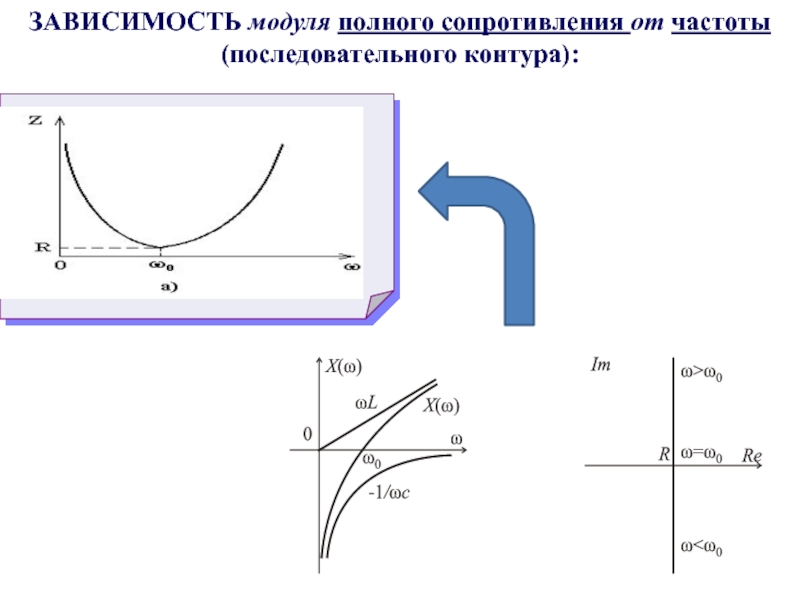
- 61. ЗАВИСИМОСТЬ модуля полного сопротивления от частоты (последовательного контура):
- 62. 6.2. В параллельном контуре возникает резонанс токов,
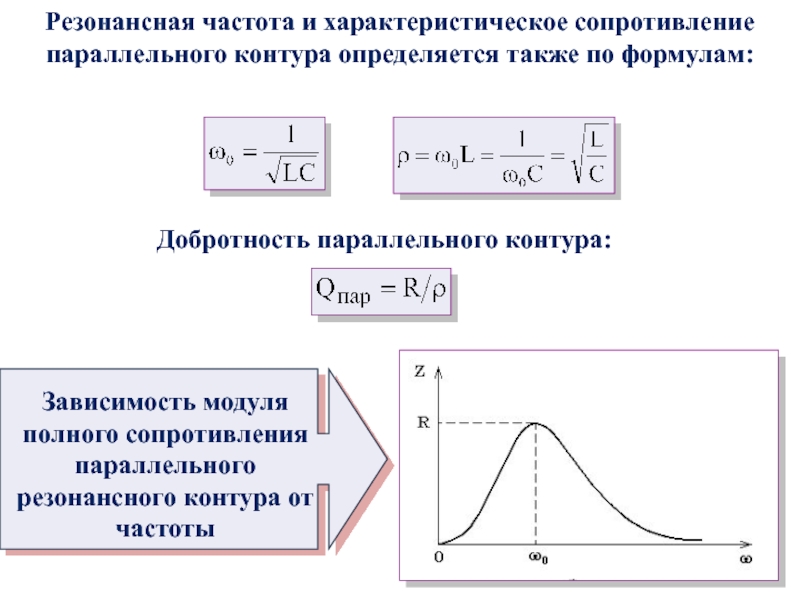
- 63. Резонансная частота и характеристическое сопротивление параллельного контура
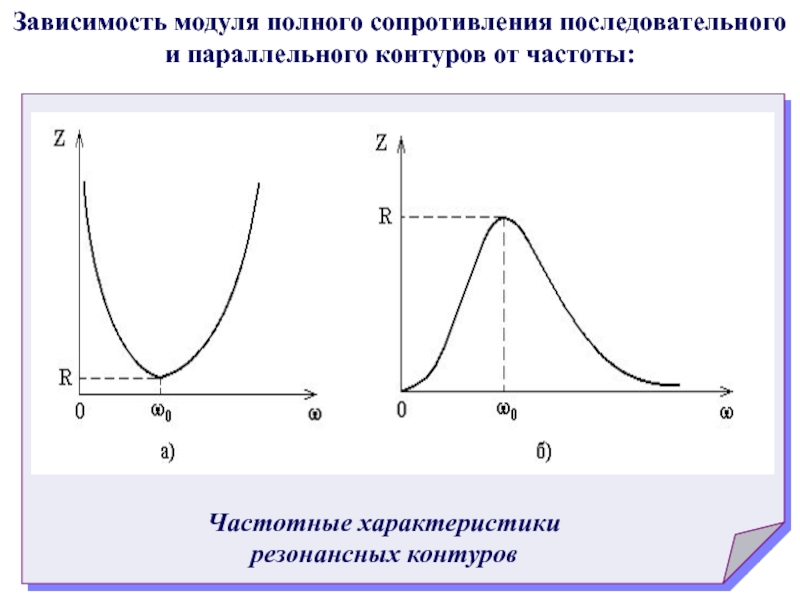
- 64. Зависимость модуля полного сопротивления последовательного и параллельного контуров от частоты: Частотные характеристики резонансных контуров
- 65. Скачать презентанцию
Слайды и текст этой презентации
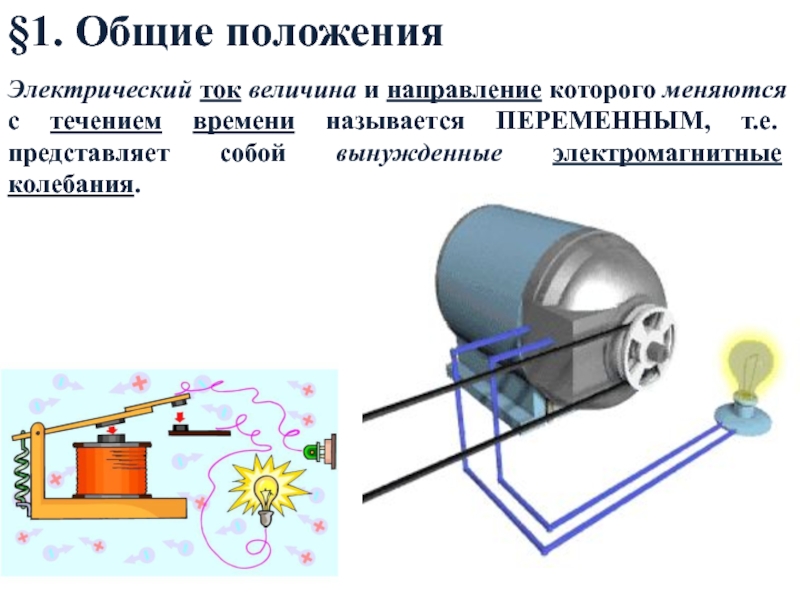
Слайд 3Электрический ток величина и направление которого меняются с течением времени
называется ПЕРЕМЕННЫМ, т.е. представляет собой вынужденные электромагнитные колебания.
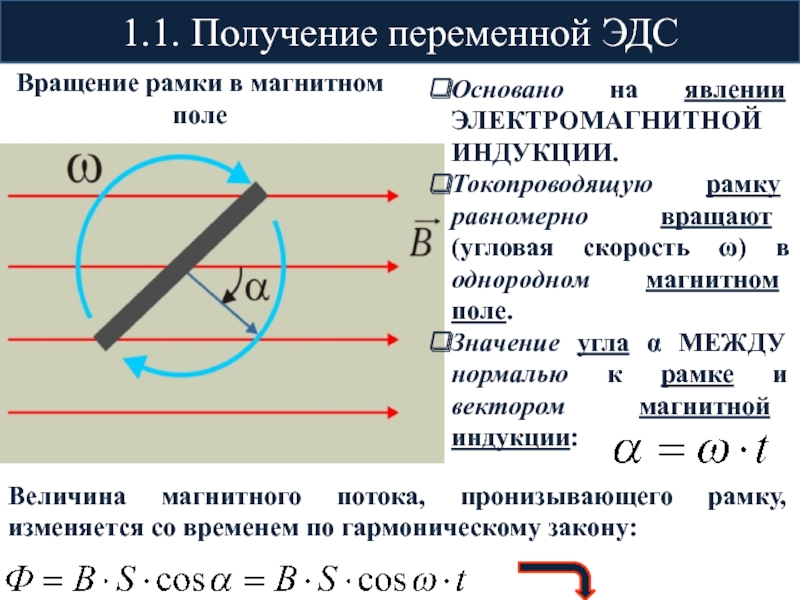
Слайд 4Основано на явлении ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ.
Токопроводящую рамку равномерно вращают (угловая
скорость ω) в однородном магнитном поле.
Значение угла α МЕЖДУ
нормалью к рамке и вектором магнитной индукции:1.1. Получение переменной ЭДС
Вращение рамки в магнитном поле
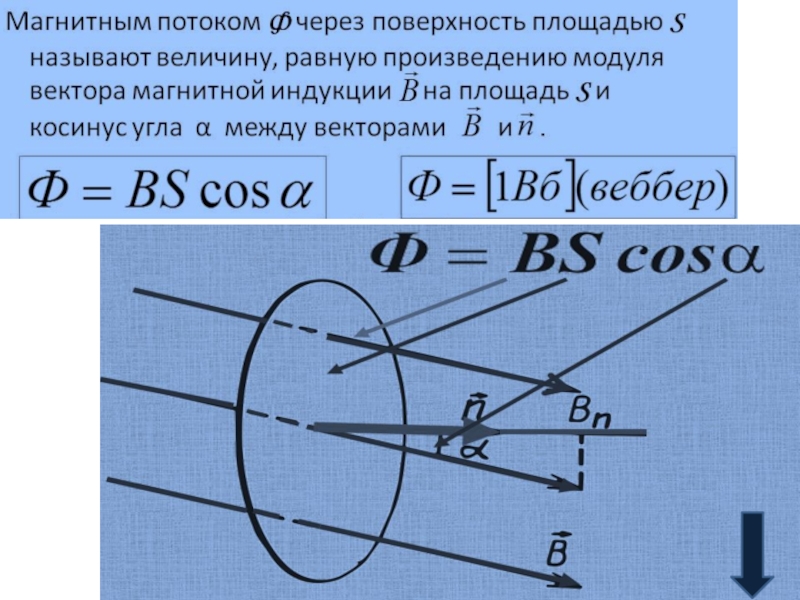
Величина магнитного потока, пронизывающего рамку, изменяется со временем по гармоническому закону:
Слайд 6Согласно ЗАКОНУ ФАРАДЕЯ для электромагнитной индукции, при изменении потока магнитной
индукции, пронизывающего контур, в контуре возникает ЭДС индукции.
максимальное
значение или амплитуда ЭДС.Если рамка содержит N витков, амплитуда возрастает в N раз.
Подключив источник переменной ЭДС к концам проводника, мы создадим на них переменное напряжение:
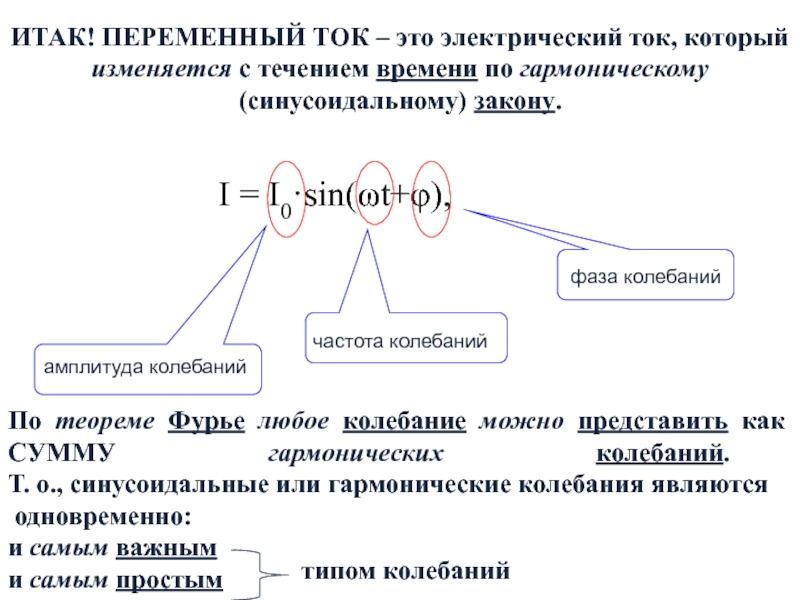
Слайд 8ИТАК! ПЕРЕМЕННЫЙ ТОК – это электрический ток, который изменяется с течением
времени по гармоническому (синусоидальному) закону.
I = I0·sin(ωt+φ),
По теореме Фурье
любое колебание можно представить как СУММУ гармонических колебаний.
Т. о., синусоидальные или гармонические колебания являютсяодновременно:
и самым важным
и самым простым
типом колебаний
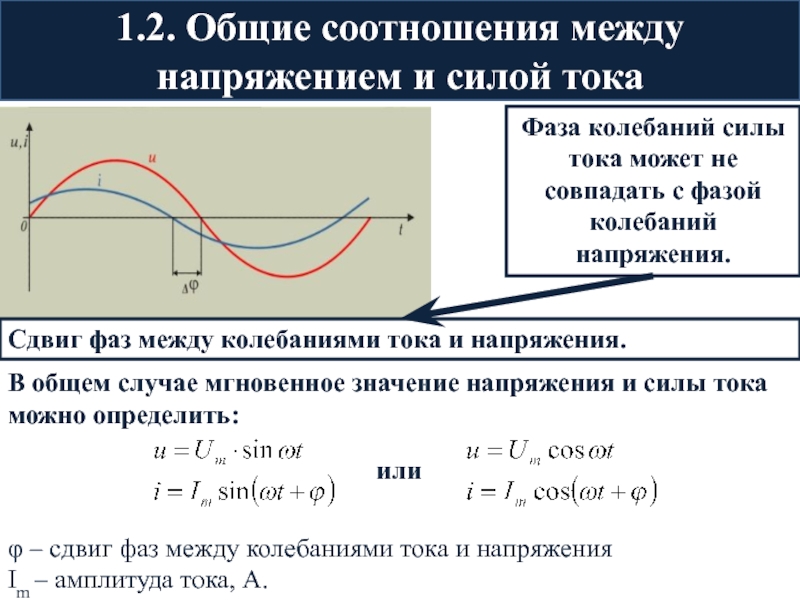
Слайд 9Фаза колебаний силы тока может не совпадать с фазой колебаний
напряжения.
Сдвиг фаз между колебаниями тока и напряжения.
или
φ – сдвиг
фаз между колебаниями тока и напряженияIm – амплитуда тока, А.
1.2. Общие соотношения между напряжением и силой тока
В общем случае мгновенное значение напряжения и силы тока можно определить:
Слайд 101.3. Действующие значения напряжения и силы тока
ФИЗИЧЕСКИЙ СМЫСЛ
Действующее значение
силы переменного тока РАВНО силе постоянного тока, выделяющего в проводнике
ТО ЖЕ количество теплоты, ЧТО и переменный ток за то же время.Действующее значение напряжения:
Слайд 11Когда говорят, что напряжение в городской электрической сети составляет 220
В, то речь идёт НЕ о мгновенном значении напряжения и
НЕ его амплитудном значении, а о ДЕЙСТВУЮЩЕМ ЗНАЧЕНИИ.Когда на электроприборах указывают силу тока, на которую они рассчитаны, то также имеют в виду действующее значение силы тока.
Слайд 12Переменный ток представляет собой вынужденные электромагнитные колебания, в которых сила
тока в цепи изменяется со временем по гармоническому закону;
Получение
переменной ЭДС в цепи основано на явлении электромагнитной индукции;ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ переменного тока и напряжения равны значениям постоянного тока и напряжения при которых в цепи с тем же активным сопротивлением выделялась бы та же энергия;
Слайд 13Для учета процессов
преобразования электромагнитной энергии
в цепях вводятся ИДЕАЛИЗИРОВАННЫЕ
ЭЛЕМЕНТЫ.
Элементы цепи рассматриваются как математические модели, СВЯЗЫВАЮЩИЕ токи и напряжения.
Общие
положения§2. Активные и реактивные элементы электрической цепи
Слайд 15ЕМКОСТЬ И ИНДУКТИВНОСТЬ являются
реактивными приемниками энергии
или
реактивными элементами.
Слайд 162.1. Активные элементы
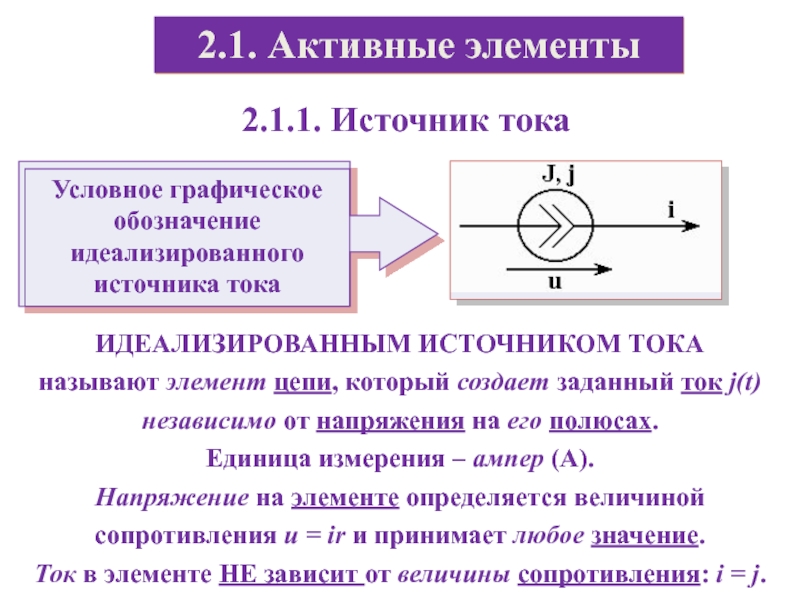
ИДЕАЛИЗИРОВАННЫМ ИСТОЧНИКОМ ТОКА
называют элемент цепи, который создает
заданный ток j(t) независимо от напряжения на его полюсах.
Единица
измерения – ампер (А). Напряжение на элементе определяется величиной сопротивления u = ir и принимает любое значение.
Ток в элементе НЕ зависит от величины сопротивления: i = j.
2.1.1. Источник тока
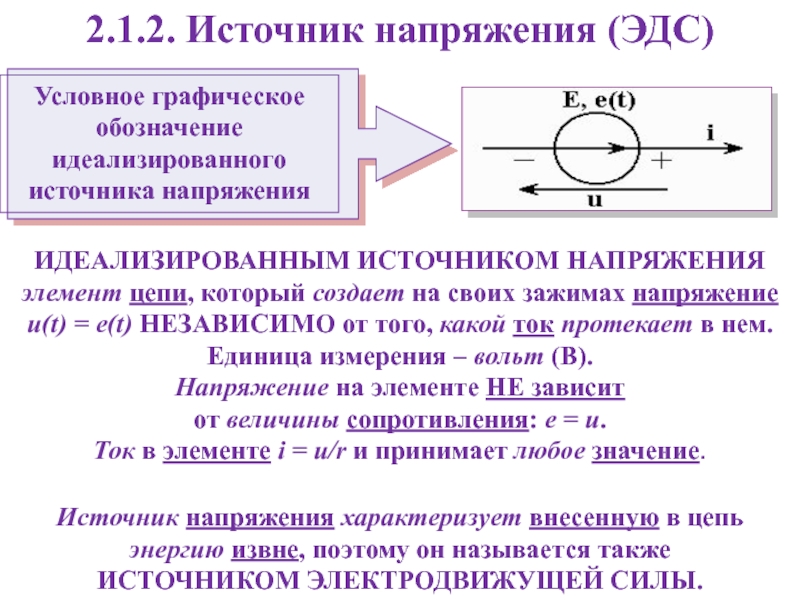
Слайд 172.1.2. Источник напряжения (ЭДС)
ИДЕАЛИЗИРОВАННЫМ ИСТОЧНИКОМ НАПРЯЖЕНИЯ
элемент цепи, который
создает на своих зажимах напряжение u(t) = e(t) НЕЗАВИСИМО от
того, какой ток протекает в нем. Единица измерения – вольт (В).Напряжение на элементе НЕ зависит
от величины сопротивления: e = u.
Ток в элементе i = u/r и принимает любое значение.
Источник напряжения характеризует внесенную в цепь энергию извне, поэтому он называется также
ИСТОЧНИКОМ ЭЛЕКТРОДВИЖУЩЕЙ СИЛЫ.
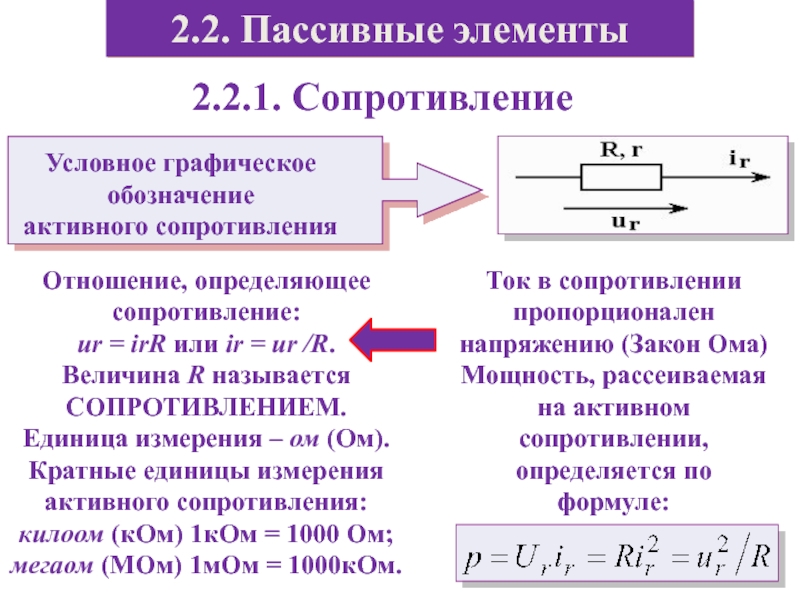
Слайд 182.2.1. Сопротивление
Отношение, определяющее сопротивление:
ur = irR или ir
= ur /R.
Величина R называется СОПРОТИВЛЕНИЕМ.
Единица измерения –
ом (Ом). Кратные единицы измерения активного сопротивления:
килоом (кОм) 1кОм = 1000 Ом;
мегаом (МОм) 1мОм = 1000кОм.
2.2. Пассивные элементы
Ток в сопротивлении пропорционален напряжению (Закон Ома)
Мощность, рассеиваемая на активном сопротивлении, определяется по формуле:
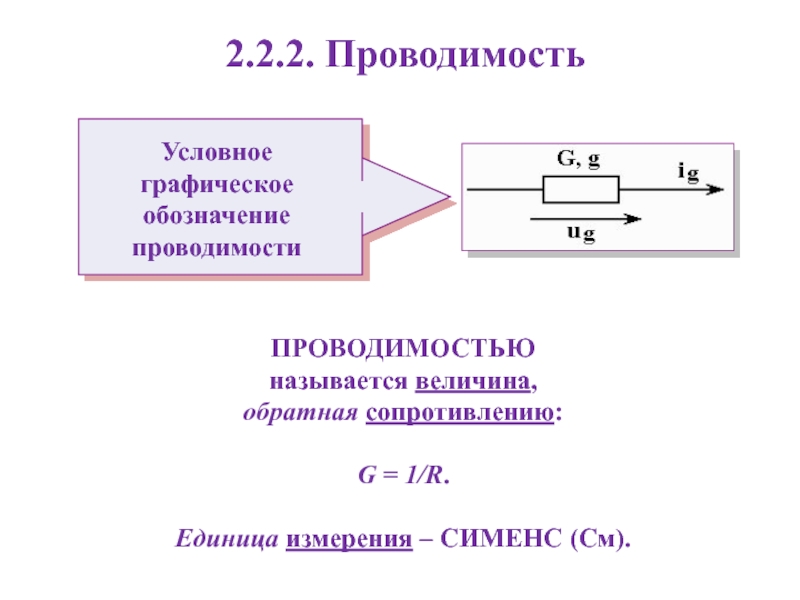
Слайд 192.2.2. Проводимость
ПРОВОДИМОСТЬЮ
называется величина,
обратная сопротивлению:
G = 1/R.
Единица измерения – СИМЕНС (См).
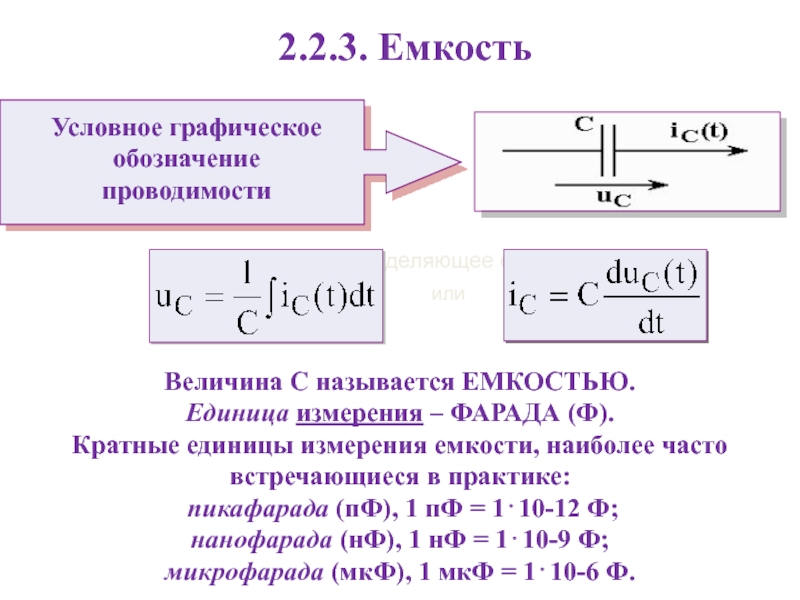
Слайд 202.2.3. Емкость
Отношение, определяющее емкость:
Величина С называется ЕМКОСТЬЮ.
Единица
измерения – ФАРАДА (Ф).
Кратные единицы измерения емкости, наиболее часто
встречающиеся в практике:пикафарада (пФ), 1 пФ = 110-12 Ф;
нанофарада (нФ), 1 нФ = 110-9 Ф;
микрофарада (мкФ), 1 мкФ = 110-6 Ф.
Слайд 21Величина заряда на конденсаторе определяется по формуле:
Q = CU,
Кл.
Таким образом,
электрическая емкость –
это коэффициент пропорциональности, связывающий
накопленный заряд Q с приложенным напряжением U.
Энергия, накапливающаяся в емкости,
определяется по формуле:
Wc = (CU2) / 2.
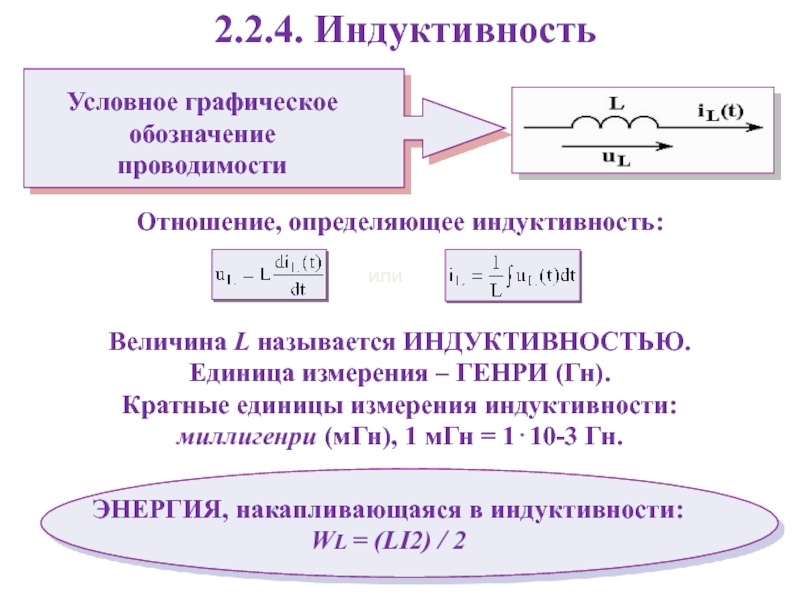
Слайд 222.2.4. Индуктивность
Отношение, определяющее индуктивность:
Величина L называется ИНДУКТИВНОСТЬЮ.
Единица
измерения – ГЕНРИ (Гн).
Кратные единицы измерения индуктивности:
миллигенри (мГн), 1
мГн = 110-3 Гн. ЭНЕРГИЯ, накапливающаяся в индуктивности:
WL = (LI2) / 2
Слайд 261) Заданное сопротивление обычно обеспечивают включением специального изделия, называемого РЕЗИСТОРОМ;
2)
Заданную емкость – включением специального изделия, называемого КОНДЕНСАТОРОМ;
3) Заданную индуктивность
– включением катушек и просто проводников.В ОТЛИЧИЕ от идеализированных элементов реальные элементы электрических цепей характеризуются множеством параметров,
часть которых можно смоделировать
с помощью эквивалентных
электрических схем (схем замещения),
составленных из идеализированных элементов.
2.4. В реальных электрических цепях:
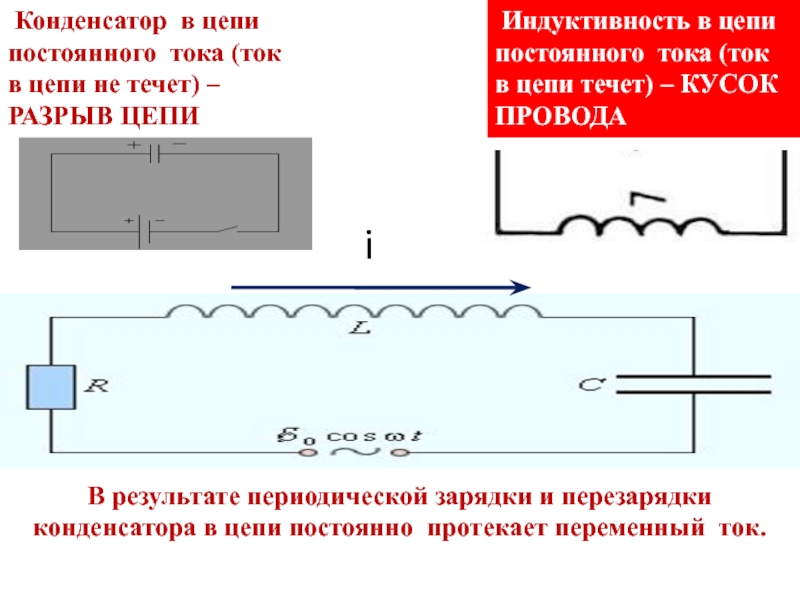
Слайд 28 Конденсатор в цепи постоянного тока (ток в цепи не
течет) – РАЗРЫВ ЦЕПИ
Индуктивность в цепи постоянного тока (ток
в цепи течет) – КУСОК ПРОВОДАi
В результате периодической зарядки и перезарядки конденсатора в цепи постоянно протекает переменный ток.
Слайд 29В цепях переменного тока различают три вида сопротивлений:
Сопротивление переменному току
со стороны материала проводника (нагревается, т.е. потребляет мощность).
В цепи переменного
тока в катушке индуктивности индуцируется э.д.с. самоиндукции (т. к. магнитный поток, пронизывающий витки катушки, изменяется) => препятствует нарастанию тока при его увеличении и уменьшению тока при спаде. Действие индуктивности при переменном токе подобно сопротивлению. С увеличением индуктивности сопротивление увеличивается. Слайд 30В цепи течет ток заряда или разряда конденсатора, величина которого
зависит от емкости конденсатора: чем больше емкость, тем больше ток
(заряда и разряда) => конденсатор можно рассматривать как некоторое сопротивление переменному току <=возникает вследствие того, что при заряде конденсатора между его обкладками возникает напряжение (Uc), направленное навстречу напряжению, которое приложено на зажимах.
Слайд 31Электрические устройства, преобразующие электрическую энергию во внутреннюю, называются
активными сопротивлениями
2.1.
Резистор в цепи переменного тока
Мгновенное значение силы тока прямо пропорционально
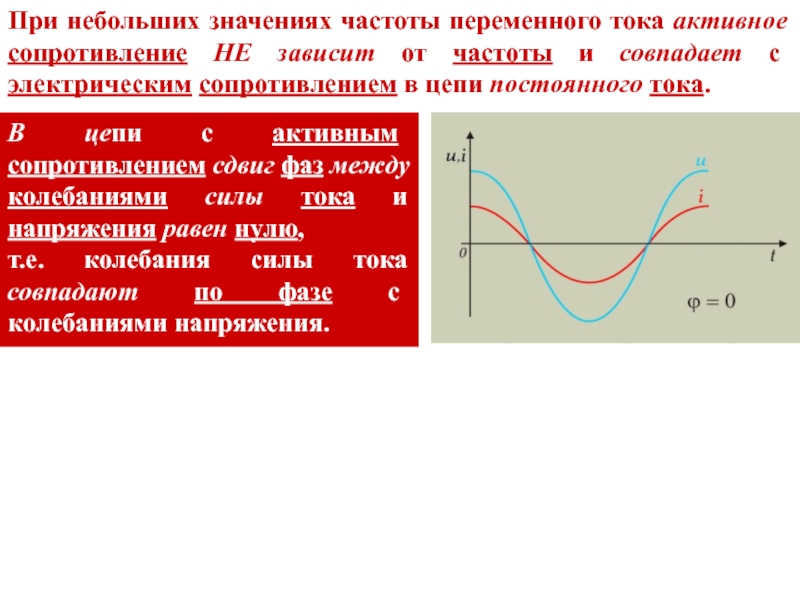
мгновенному значению напряжения - по закону Ома :Слайд 32При небольших значениях частоты переменного тока активное сопротивление НЕ зависит
от частоты и совпадает с электрическим сопротивлением в цепи постоянного
тока.В цепи с активным сопротивлением сдвиг фаз между колебаниями силы тока и напряжения равен нулю,
т.е. колебания силы тока совпадают по фазе с колебаниями напряжения.
Слайд 33 2.2. Векторная диаграмма при наличии в цепи переменного тока
только активного сопротивления
Амплитуду колебаний напряжения в цепи переменного тока можно
выразить МЕТОДОМ ВЕКТОРНЫХ ДИАГРАММ. Выберем ось Х диаграммы таким образом, чтобы вектор, изображающий колебания тока, был направлен вдоль этой оси. В дальнейшем мы будем называть ее ОСЬЮ ТОКОВ.
Так как угол φ между колебаниями напряжения и тока на резисторе равен нулю, то вектор, изображающий колебания напряжения на сопротивлении R, будет направлен вдоль оси токов. Длина его равна Im·R.
Слайд 342.3. Конденсатор в цепи переменного тока
Пусть на конденсатор подано напряжение
φА-φВ = U = q/C,
НО! Так как I =
dq/dt, тоI = I0·sinωt
Поскольку ток меняется по закону,
Тогда
Постоянная интегрирования q0 - заряд, не связанный с колебаниями тока, поэтому можно считать q0 = 0.
=0
Слайд 35ОТСЮДА
Следовательно, колебания напряжения на обкладках конденсатора в цепи переменного тока
отстают по фазе от колебаний силы тока на π/2 =>
В
момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того как напряжение достигает максимума, сила тока становится равной нулю и т.д.
Физический смысл: ЧТОБЫ возникло напряжение на конденсаторе, должен натечь заряд за счет протекания тока в цепи. ОТСЮДА - отставание напряжения.
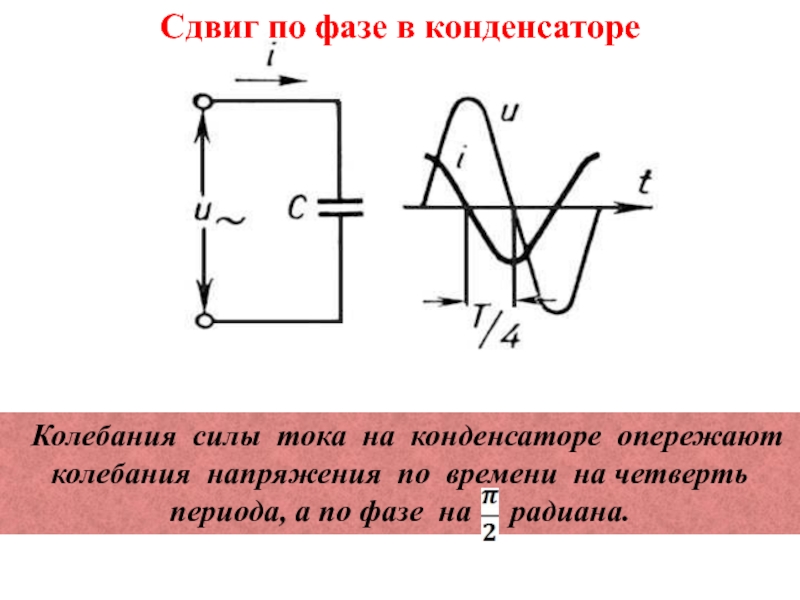
Слайд 36 Колебания силы тока на конденсаторе опережают колебания напряжения по
времени на четверть периода, а по фазе на
радиана.Сдвиг по фазе в конденсаторе
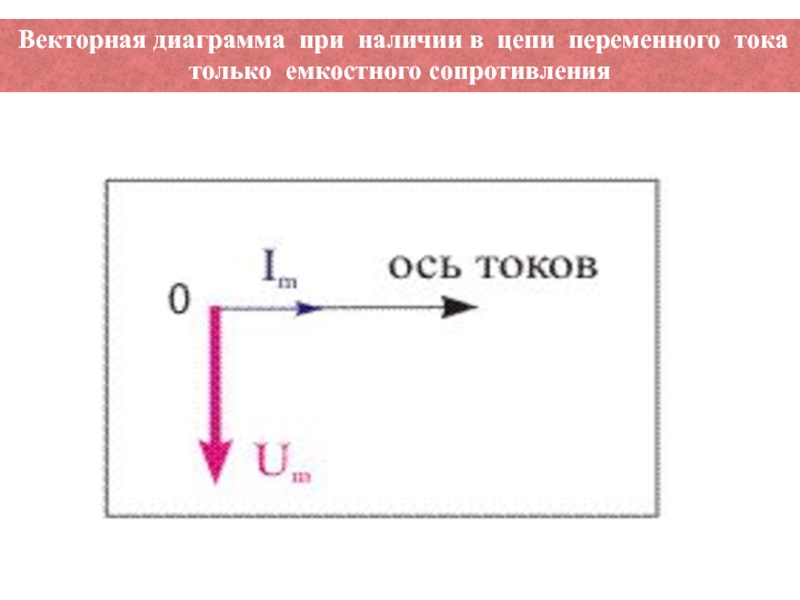
Слайд 37Отношение амплитуды колебаний напряжения на конденсаторе к амплитуде колебаний силы
тока называют емкостным сопротивлением конденсатора (обозначается XC):
Величина
а по закону Ома
U = I·R играет роль сопротивления участка цепи
Она называется ЕМКОСТНЫМ СОПРОТИВЛЕНИЕМ
векторная диаграмма
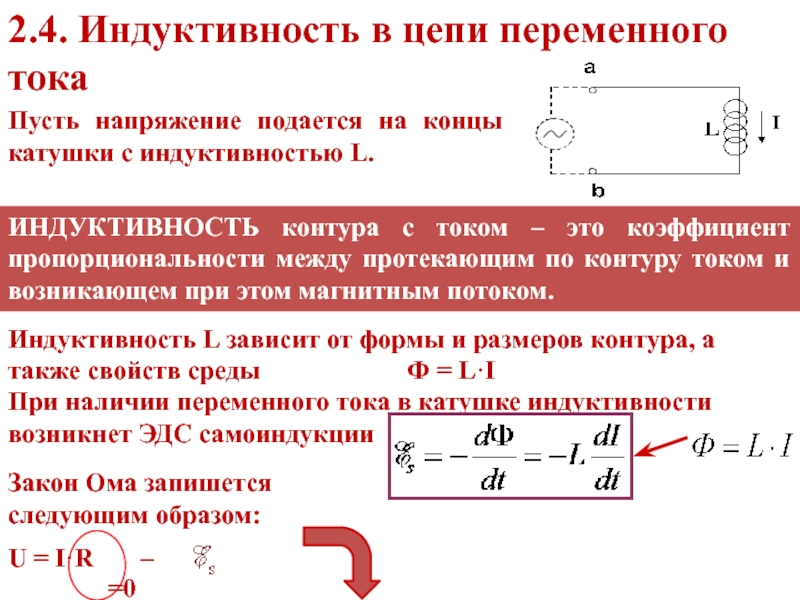
Слайд 392.4. Индуктивность в цепи переменного тока
Индуктивность L зависит от
формы и размеров контура, а также свойств среды
Ф = L·IПусть напряжение подается на концы катушки с индуктивностью L.
ИНДУКТИВНОСТЬ контура с током – это коэффициент пропорциональности между протекающим по контуру током и возникающем при этом магнитным потоком.
При наличии переменного тока в катушке индуктивности возникнет ЭДС самоиндукции
Закон Ома запишется следующим образом:
U = I·R –
=0
Слайд 40ТОГДА:
Таким образом, колебания напряжения на индуктивности ОПЕРЕЖАЮТ колебания тока на
π/2.
Физический смысл: R=0, внешнее напряжение уравновешивает ЭДС самоиндукции U
= – . Но пропорциональна НЕ мгновенному значению тока, А быстроте его изменения, которая будет макс. когда ток проходит через ноль.
Поэтому нулевые значения ТОКА СОВПАДАЮТ с макс. U
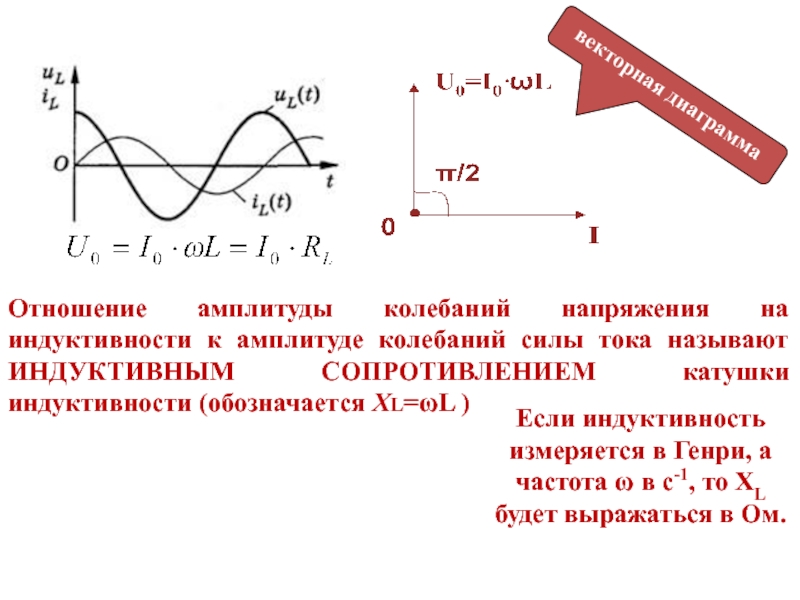
Слайд 41векторная диаграмма
Если индуктивность измеряется в Генри, а частота ω в
с-1, то ХL будет выражаться в Ом.
Отношение амплитуды колебаний напряжения
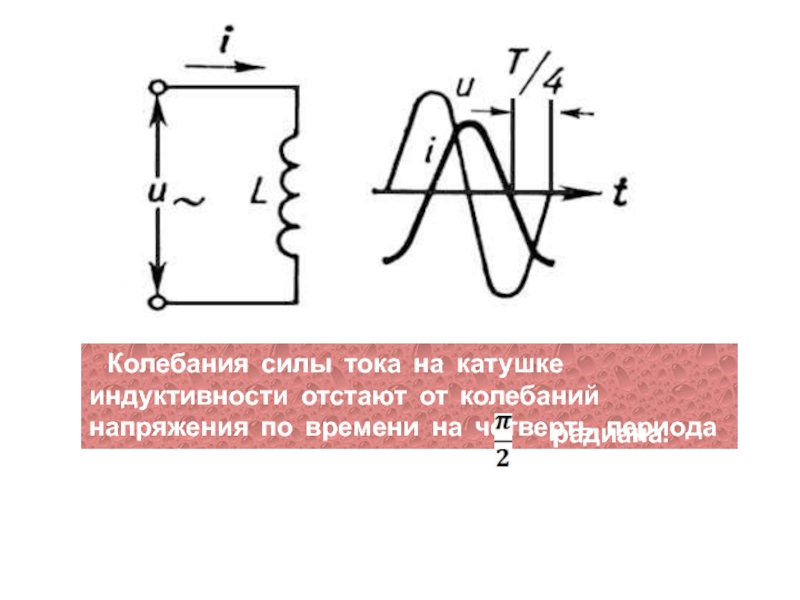
на индуктивности к амплитуде колебаний силы тока называют ИНДУКТИВНЫМ СОПРОТИВЛЕНИЕМ катушки индуктивности (обозначается XL=ωL )Слайд 42 Колебания силы тока на катушке индуктивности отстают от
колебаний напряжения по времени на четверть периода , а по
фазе нарадиана.
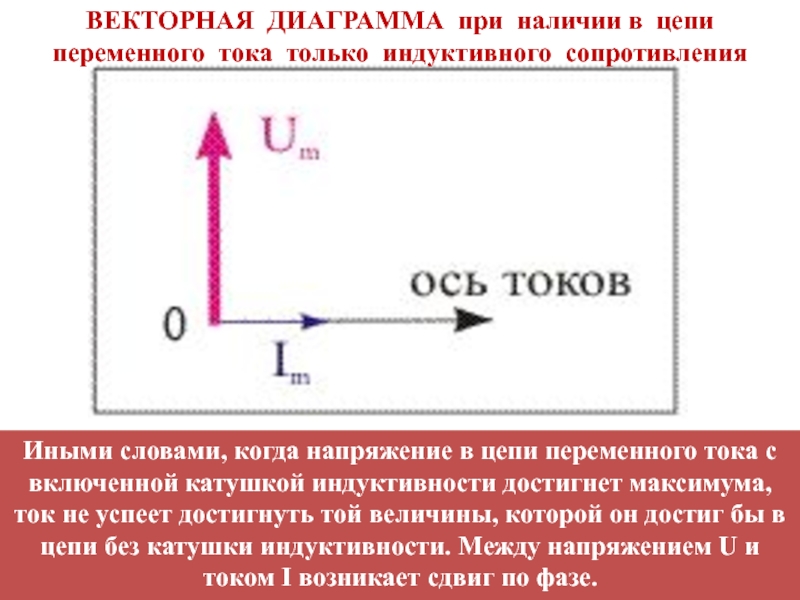
Слайд 43ВЕКТОРНАЯ ДИАГРАММА при наличии в цепи переменного тока только индуктивного
сопротивления
Иными словами, когда напряжение в цепи переменного тока с включенной
катушкой индуктивности достигнет максимума, ток не успеет достигнуть той величины, которой он достиг бы в цепи без катушки индуктивности. Между напряжением U и током I возникает сдвиг по фазе.Слайд 442.5. Закон Ома для переменного тока
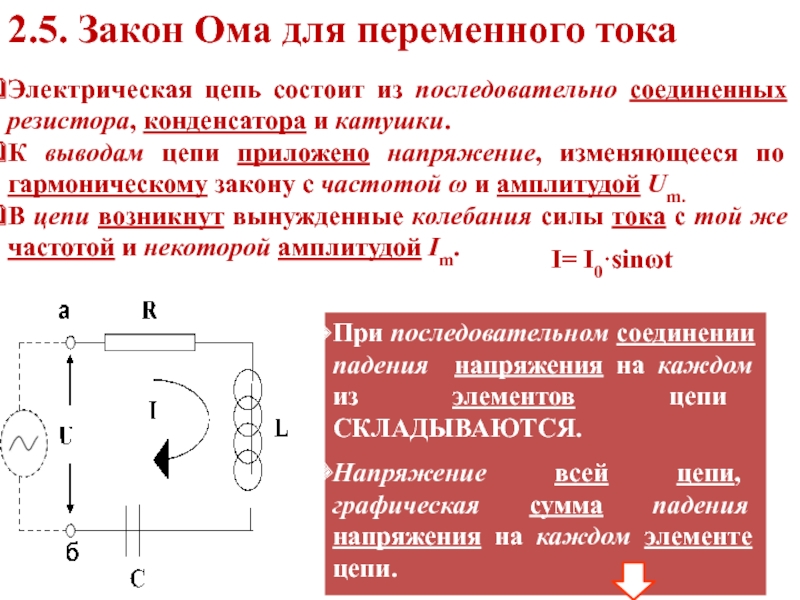
Электрическая цепь состоит из
последовательно соединенных резистора, конденсатора и катушки.
К выводам цепи приложено
напряжение, изменяющееся по гармоническому закону с частотой ω и амплитудой Um.В цепи возникнут вынужденные колебания силы тока с той же частотой и некоторой амплитудой Im.
I= I0·sinωt
При последовательном соединении падения напряжения на каждом из элементов цепи СКЛАДЫВАЮТСЯ.
Напряжение всей цепи, графическая сумма падения напряжения на каждом элементе цепи.
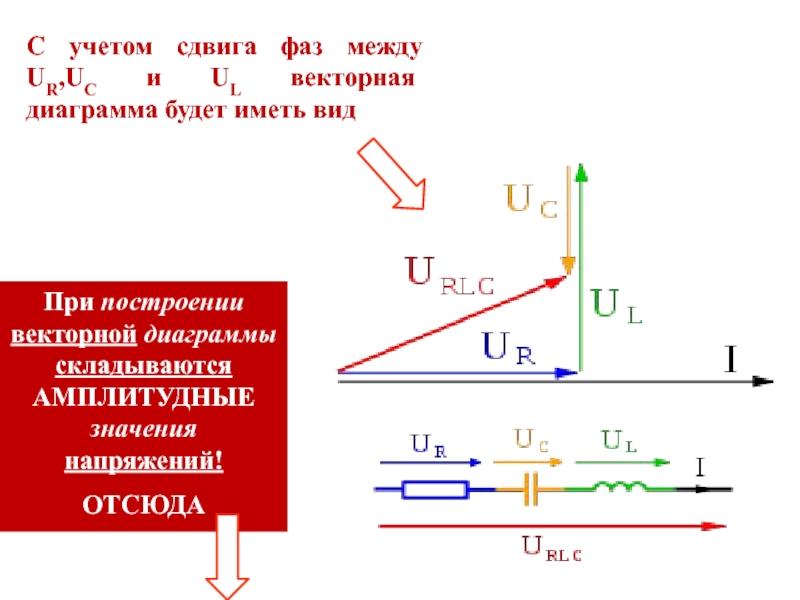
Слайд 45С учетом сдвига фаз между UR,UC и UL векторная диаграмма
будет иметь вид
При построении векторной диаграммы складываются АМПЛИТУДНЫЕ значения
напряжений!ОТСЮДА
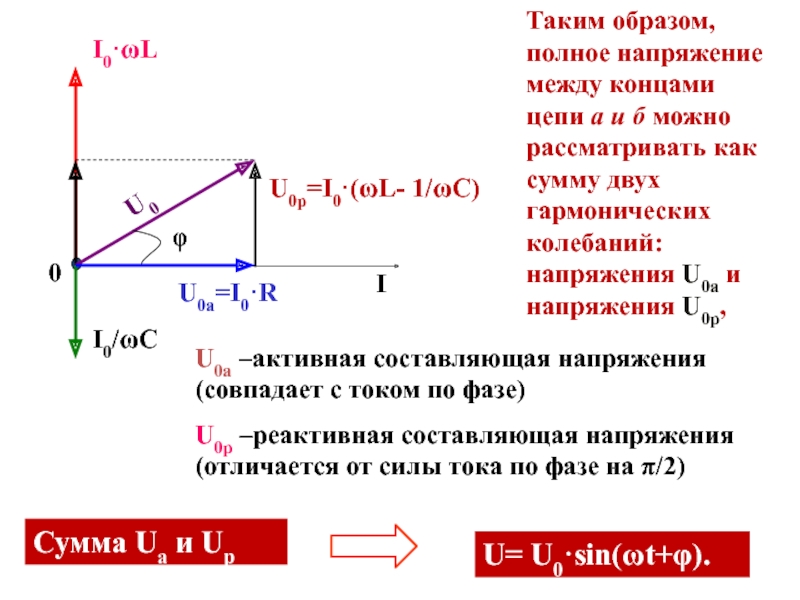
Слайд 46Таким образом, полное напряжение между концами цепи а и б
можно рассматривать как сумму двух гармонических колебаний: напряжения U0а и
напряжения U0р,U0а –активная составляющая напряжения (совпадает с током по фазе)
U0р –реактивная составляющая напряжения (отличается от силы тока по фазе на π/2)
U= U0·sin(ωt+φ).
Сумма Uа и Uр
Слайд 47Амплитуду полного напряжения можно найти как модуль суммы векторов:
Напряжения
UR,UC и UL в сумме равны приложенному U. => Cложив
векторы UR,UC и UL, получаем вектор, длиной U0Полный закон Ома для переменного тока
Z - полное сопротивление цепи или ИМПЕДАНС
Слайд 48Вектор U0 образует с осью токов угол φ, тангенс которого
равен:
– активное сопротивление цепи. Активное сопротивление всегда ПРИВОДИТ к
выделению тепла Джоуля-Ленца.– реактивное сопротивление цепи. Наличие реактивного сопротивления НЕ СОПРОВОЖДАЕТСЯ выделением тепла.
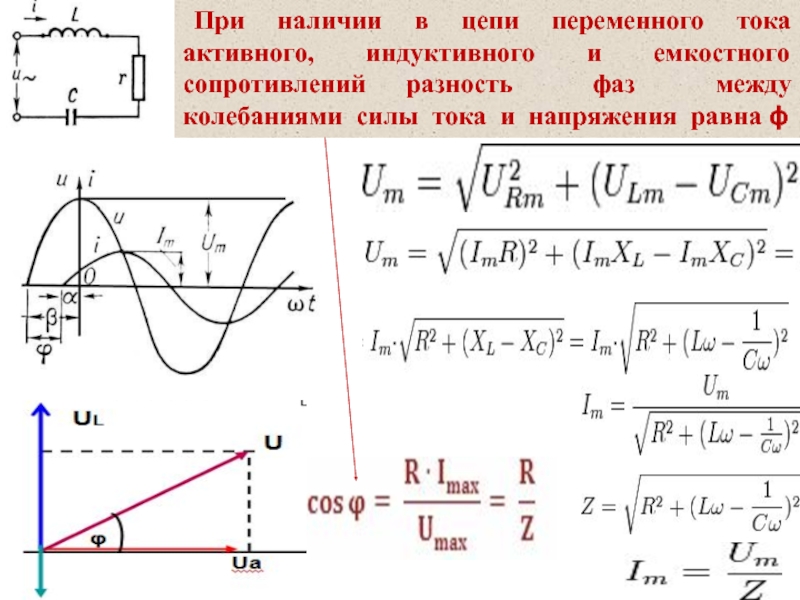
Слайд 49 При наличии в цепи переменного тока активного, индуктивного и
емкостного сопротивлений разность фаз между колебаниями силы тока и напряжения
равна ϕСлайд 50§4. Синусоидальные функции в комплексной форме
Комплексное число м. б.
в показательной или алгебраической форме:
Где у комплексного числа:
с
– модуль, φ- аргумент;
a - вещественная часть, b - мнимая часть, j - мнимая единица, j = √-1.
Формула Эйлера - переход от показательной к алгебраической.
От алгебраической к показательной
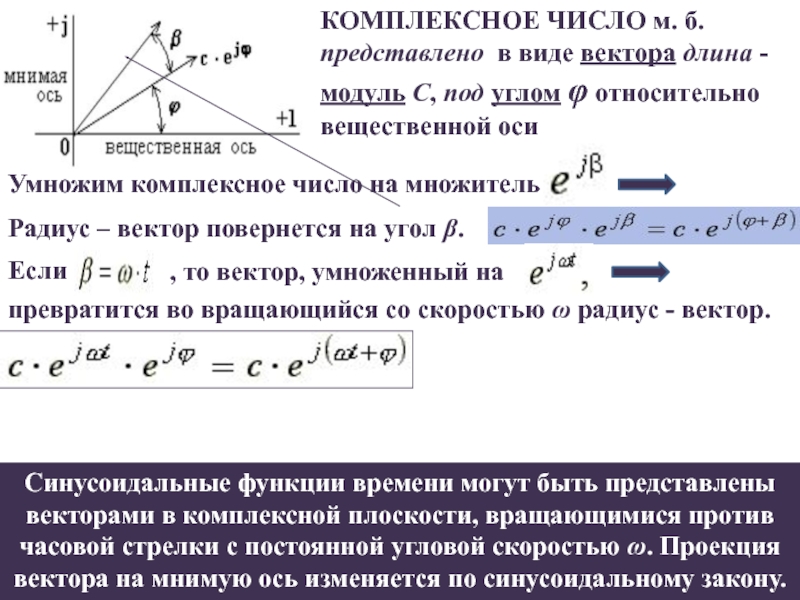
Слайд 51КОМПЛЕКСНОЕ ЧИСЛО м. б. представлено в виде вектора длина -
модуль C, под углом φ относительно вещественной оси
Умножим комплексное
число на множитель Радиус – вектор повернется на угол β.
, то вектор, умноженный на
превратится во вращающийся со скоростью ω радиус - вектор.
Если
Синусоидальные функции времени могут быть представлены векторами в комплексной плоскости, вращающимися против часовой стрелки с постоянной угловой скоростью ω. Проекция вектора на мнимую ось изменяется по синусоидальному закону.
Слайд 53 Действующие значения напряжения и силы тока фиксируются электроизмерительными
приборами и позволяют непосредственно вычислять мощность переменного тока .
Мощность в цепи ПЕРЕМЕННОГО ТОКА определяется теми же соотношениями, что и мощность ПОСТОЯННОГО ТОКА, в которые вместо силы постоянного тока и постоянного напряжения - соответствующие ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ:Когда между напряжением и силой тока СДВИГ ФАЗ, мощность определяется по формуле:
§5. Мощность в цепи переменного тока
Слайд 55 1.Если в цепи переменного тока только АКТИВНОЕ сопротивление, то
выделяемая мощность максимальна. Активное сопротивление энергию из сети полностью превращает
во внутреннюю, обратно в сеть не возвращается.2.Если в цепи только ЕМКОСТНОЕ сопротивление, то конденсатор энергию, получаемую от сети, полностью превращает в энергию электрического поля конденсатора, затем эта энергия обратно полностью возвращается в сеть.
3.Если в цепи только ИНДУКТИВНОЕ сопротивление, катушка индуктивности энергию, получаемую от сети, полностью превращает в энергию магнитного поля вокруг катушки, затем эта энергия обратно полностью возвращается в сеть.
4.Если в цепи АКТИВНОЕ, ИНДУКТИВНОЕ, ЕМКОСТНОЕ сопротивления - мощность (выделяемое тепло) максимальная. Активное сопротивление часть энергии, получаемое от сети, превращает во внутреннюю энергию, конденсатор и катушка индуктивности энергию обратно возвращают в сеть.
Слайд 56МОЩНОСТЬ в цепи переменного тока определяется теми же соотношениями, что
и мощность постоянного тока, в которые ВМЕСТО силы постоянного тока
и постоянного напряжения подставляют соответствующие действующие значения.Слайд 57явление в электрической цепи,
содержащей индуктивные и емкостные элементы,
возникающее
в случае, когда реактивное сопротивление или реактивная проводимость этой цепи
равна нулю:BC BL = 0
XL XC = 0
или
§6. Резонанс
При резонансе цепь имеет место чисто активное сопротивление или проводимость:
Следовательно:
напряжение и ток в цепи совпадают по фазе,
реактивная мощность равна нулю.
Слайд 58Цепи, в которых используется эффект резонанса, называются
РЕЗОНАНСНЫМИ КОНТУРАМИ
То
есть, резонанс возникает, когда частота внешнего возмущения равна параметру
цепи, называемомуРЕЗОНАНСНОЙ ЧАСТОТОЙ 0
Различают
ПОСЛЕДОВАТЕЛЬНЫЕ и ПАРАЛЛЕЛЬНЫЕ
резонансные контуры
Условие возникновения резонанса:
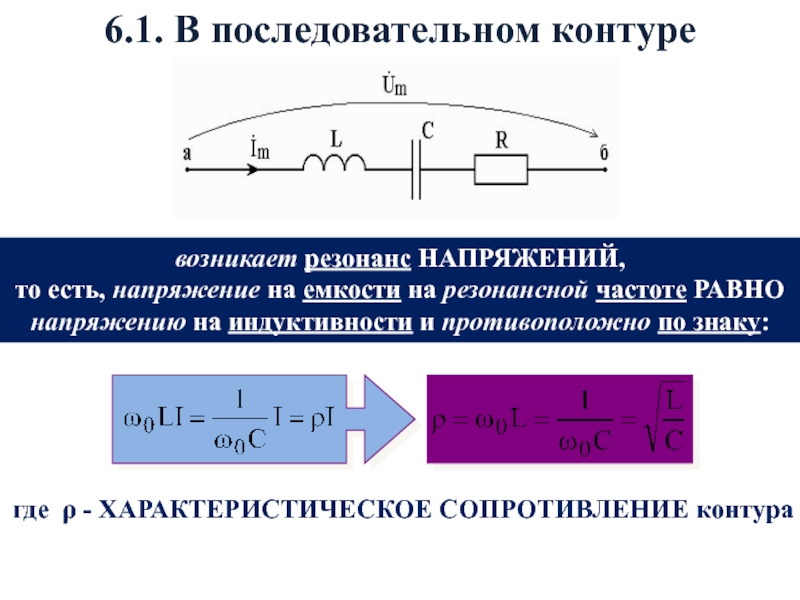
Слайд 59где - ХАРАКТЕРИСТИЧЕСКОЕ СОПРОТИВЛЕНИЕ контура
6.1. В последовательном контуре
возникает резонанс НАПРЯЖЕНИЙ,
то есть, напряжение на емкости на резонансной
частоте РАВНО напряжению на индуктивности и противоположно по знаку: Слайд 60Отношение величины электромагнитной энергии, запасенной на реактивных элементах, к энергии,
рассеиваемой на активном сопротивлении контура, называется
ДОБРОТНОСТЬЮ КОНТУРА
Для ПОСЛЕДОВАТЕЛЬНОГО
контура ДОБРОТНОСТЬ определяется: Qпосл = /R
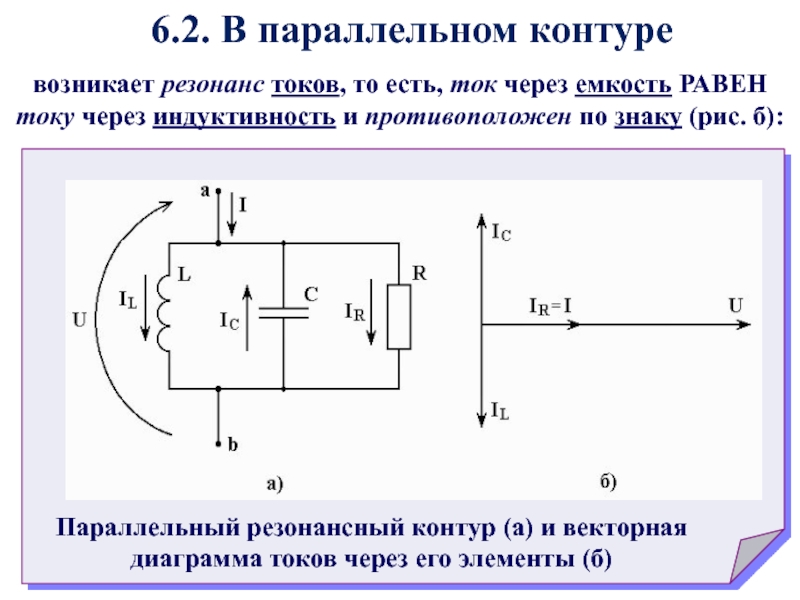
Слайд 626.2. В параллельном контуре
возникает резонанс токов, то есть, ток
через емкость РАВЕН току через индуктивность и противоположен по знаку
(рис. б):Параллельный резонансный контур (а) и векторная диаграмма токов через его элементы (б)