TheSlide.ru

Уравнение вида называется ДУ второго порядка. где х – независимая переменная

Содержание

1. Уравнение вида называется ДУ второго порядка. где х – независимая переменная
2. Будем рассматривать уравнения второго порядка, разрешенные относительно
3. ТЕОРЕМА КОШИ(о существовании и единственности решения ДУ)Пусть
4. Через заданную точку (х0 ,у0 ) на
5. Слайд 5
6. Общим решением уравнения (6) в некоторой области
7. Пример.Рассмотрим уравнениеЕго общее решение получается при двукратном интегрировании:
8. Найдем частное решение уравнения при Подставляем в общее решение:Частное решение будет иметь вид:
9. Скачать презентанцию

Будем рассматривать уравнения второго порядка, разрешенные относительно второй производной:6Решением ДУ второго порядка называетсяфункция у=φ(х), определенная нанекотором интервале (a,b), котораяпри подстановке ее в уравнениеобращает его в тождество.

Главная
Разное
Уравнение вида называется ДУ второго порядка. где х – независимая переменная

Слайды и текст этой презентации

Слайд 1Уравнение вида
называется ДУ второго порядка.
где х – независимая переменная;
у– неизвестная

функция;
у' и у"– ее первая и вторая производные.
21.5. ДУ ВТОРОГО

ПОРЯДКА

Уравнение виданазывается ДУ второго порядка.где х – независимая переменная;у– неизвестная функция;у' и у

Слайд 2Будем рассматривать уравнения второго порядка, разрешенные относительно второй производной:
6
Решением ДУ

второго порядка называется
функция у=φ(х), определенная на
некотором интервале (a,b), которая
при подстановке

ее в уравнение
обращает его в тождество.

Будем рассматривать уравнения второго порядка, разрешенные относительно второй производной:6Решением ДУ второго порядка называетсяфункция у=φ(х), определенная нанекотором интервале

Слайд 3ТЕОРЕМА КОШИ
(о существовании и единственности решения ДУ)
Пусть дано ДУ (6).

Если функция f(x,y,у') и ее
частные производные f'y и f'y' непрерывны
в

некоторой области D пространства
переменных (х,у,у'), то для любой
внутренней точки (х0,у0,у'0) этой области
существует единственное решение
уравнения, удовлетворяющее начальным
условиям х=х0, у=у0, у‘=у'0

ТЕОРЕМА КОШИ(о существовании и единственности решения ДУ)Пусть дано ДУ (6). Если функция f(x,y,у') и еечастные производные f'y

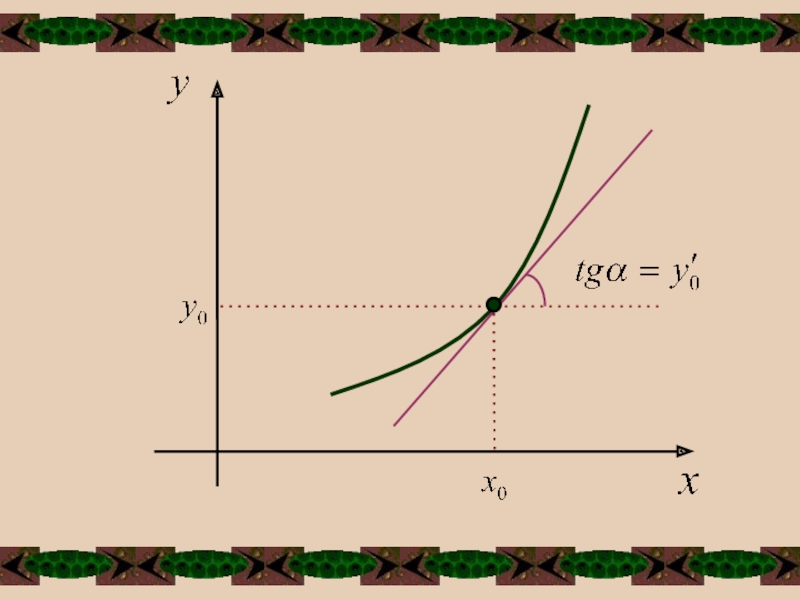
Слайд 4Через заданную точку (х0 ,у0 ) на плоскости ХОУ проходит

единственная интегральная кривая с заданным значением углового коэффициента касательной у0'

.

Геометрический смысл теоремы Коши:

Через заданную точку (х0 ,у0 ) на плоскости ХОУ проходит единственная интегральная кривая с заданным значением углового

Слайд 5

Слайд 6Общим решением уравнения (6) в некоторой области D называется функция

удовлетворяющая этому уравнению при произвольных значениях С1 и С2.
Частным решением

уравнения (6) называется общее решение, взятое при фиксированных значениях этих постоянных:

Общим решением уравнения (6) в некоторой области D называется функция удовлетворяющая этому уравнению при произвольных значениях С1

Слайд 7Пример.
Рассмотрим уравнение
Его общее решение получается при двукратном интегрировании:

Пример.Рассмотрим уравнениеЕго общее решение получается при двукратном интегрировании:

Слайд 8Найдем частное решение уравнения при
Подставляем в общее решение:
Частное решение

будет иметь вид:

Найдем частное решение уравнения при Подставляем в общее решение:Частное решение будет иметь вид:

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей